两维电场和电流的可视化

邱为钢 张 萍

（1湖州师范学院理学院，浙江 湖州 313000；2北京师范大学物理学系，北京 100875）

在两维平面存在一个区域D，里面有电荷分布，一般情况下是点电荷体系，或者有电流分布，为保准电流守恒，注入的总电流等于流出的总电流.在区域D的边界B上，电势为零或电流垂直边界的分量为零.区域D上的电势解析表达式，可以用镜像电荷法[1]或保角变换法[2-4]求解.这种方法的关键之处是，存在解析形式的保角变换，把区域D变换到上半复平面W，譬如常见的圆盘形，以及文献[2～4]中的大小圆相切的月牙形、圆弧与弦组成的弓形等.由保角变换的性质可知，区域D的等势线（电场线）和上半复平面W上的等势线（电场线）存在一一对应关系，只要一个区域上等势线有解析表达式，就能方便地利用数学软件画出另一个区域上的等势线.利用文献[5]、文献[6]上保角变换，我们给出了点电荷在正方形（正三角形）中心时，正方形（正三角形）上的等势线（电场线）的图形，也给出了电流从正方形（正三角形）一个顶点流入，从另一个顶点流出时，正方形（正三角形）上的等势线（电流线）的图形.为统一符号，区域D上的坐标为z＝x＋iy，上半复平面W上的坐标w＝u＋iv.

下面分3种情况进行讨论.

（1）存在一个保角变换w＝f（z），把区域D映射到上半复平面W，把区域D的边界B映射为W平面上的实轴，电荷所在点z0映射到w0＝f（z0）.取电荷密度和其他物理常数为归一化单位，则满足边界上电势为零，即Dirichlet边界条件的复势是

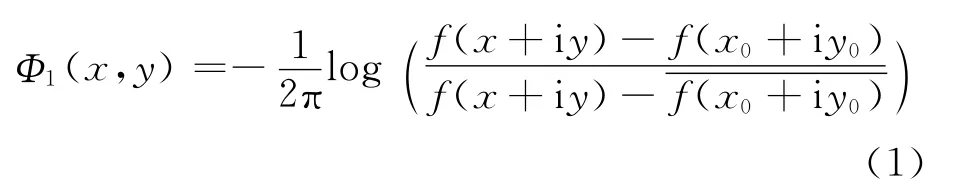
设电流注入（流出）位置为za＝xa＋iya，电流强度为Ia（正号代表注入，负号代表流出），取电流密度和其他物理常数为归一化单位，则满足垂直边界电流分量为零，即Neumann边界条件的复势是

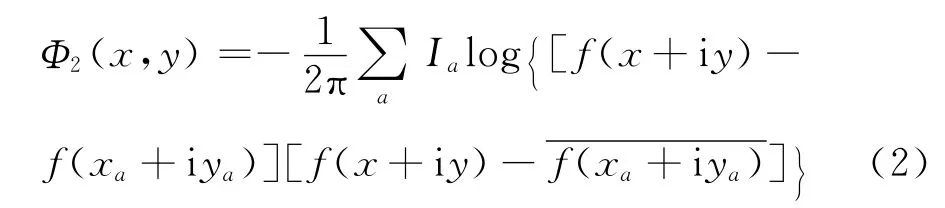
式（1）或式（2）的实部为常数的就是等势线，虚部为常数的就是电场线或电流线.我们直接用数学软件表示和处理式（1）、式（2），一是数值运算的对象本来就是复数，所有的函数都能对复数作运算；二是给出f（z）的表达式，纸面上写出式（1）、式（2）的实部和虚部费很大空间，数学软件一行代码就能处理，这也是本文很少给出具体表达式的原因；三是不少数学软件有画等值线的直接指令，方便拿过来使用.我们给出一个简单例子，电流从圆盘边界上一点z1＝1注入，电流强度为I1＝1.在边界上两点z2＝exp 2πi／（ 3）和z3＝exp-2πi／（ 3）流出，电流强度为I2＝I3＝-1／2.取单位圆到上半复平面的保角映射为f（z）＝i（1-z）／（1＋z），代入式（2），得到圆盘上的等势线（虚线）和电流线（带箭头）如图1所示.

由图1可以看出，靠近圆盘边界处，电流平行于边界，即垂直边界的电流分量为零，等势线垂直于电流线，这符合电流分布的物理规律.

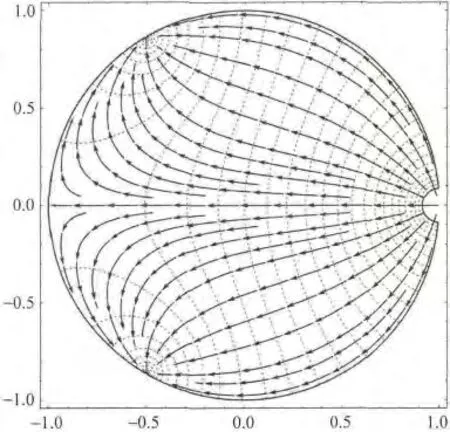
图1 边界上有电流注入（流出）圆盘上的等势线和电流

（2）从上半复平面W到区域D上的保角变换存在解析表达式.这样，只要给出上半复平面W上的等势线（电场线）的参数表达式，保角变换就能把它们映射到区域D上的等势线和电流线.如果上半复平面W上只有单个电荷，电势在实轴上为零，或者两个电流源只分布在实轴上，那么等势线上的点到镜像电荷所在点距离之比为常数；电场（电流）线上的点到镜像电荷所在点辐角之差为常数.由中学解析几何知识可知，这两组线是正交的圆.假定镜像电荷所在点的坐标是（0，-a），（0，a），那么等势线的参数方程是

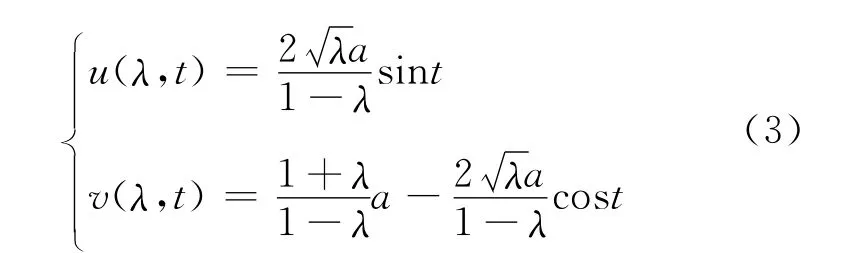
其中，λ＜1是等势线的参数，0＜t＜π是参数角.电场线的参数方程是

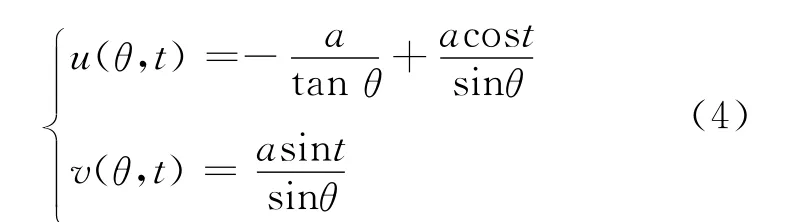
其中，θ是电场线的参数，0＜t＜π是参数角.假定镜像电荷所在点的坐标是 （-a，0），（a，0），那么等势线的参数方程是

其中，λ是等势线的参数，0＜t＜π是参数角.电场线的参数方程是

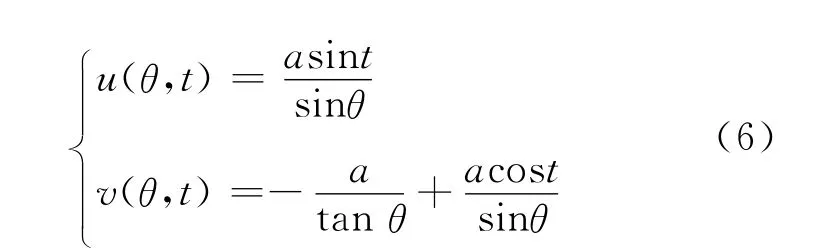
其中，θ是电场线的参数，-θ＜t＜θ是参数角.

先讨论上半复平面到矩形的保角变换，由文献[5]可知，

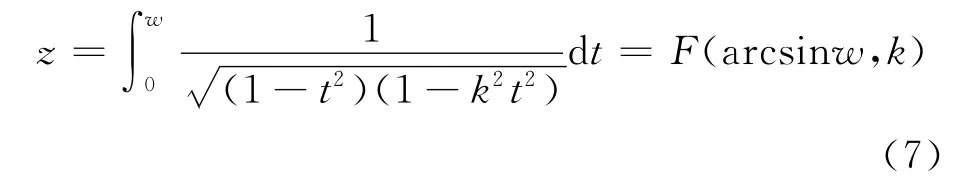
其中，F（φ，k）是第一类不完全椭圆积分.这个变换把上半复平面W变换为z平面上的矩形，特别是把上半复平面W实轴上（-1，1，1／k，-1／k）4个点变换为 （-K，K，K＋iK′，-K＋iK′），即矩形 的 4 个 顶 点，其 中K＝F（π／2，k），K′＝这个变换还把零映射为映射为iK′／2，无穷远点映射为iK′.为简单美观，我们取正方形，点电荷位于中心，此时，把式（3）、式（4）代入式（7），得到正方形上中心处点电荷所产生的等势线和电场线如图2所示.

由图2可以看出，越靠近电荷，原点附近的等势线越接近圆形，越靠近边界，等势线越接近于正方形；电场线垂直于等势线，特别在边界处，电场线垂直于正方形，电势（场）线具有正方形对称性.这些图形性质，符合正方形上中心点电荷所产生电势的分布规律.

正方形的顶点上注入和流出电流，设注入点为（-K，0），流出点为 （K，0）或 （K，K′），取a＝1或把式（5）、式（6）代入式（7），得到正方形上电流产生的等势线和电场线如图3、图4所示.

图2 正方形中心处点电荷的等势线和电场线

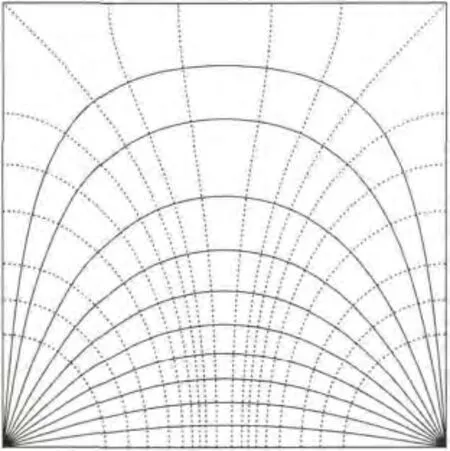
图3 正方形上电流产生的等势线和电流线

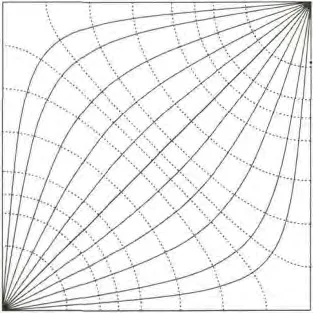
图4 正方形上电流产生的等势线和电流线

由图3、图4可以看出，越靠近电流流入（出）点，等势线越接近圆形，在边界处，等势线垂直于边界；越靠近边界，电流线越接近于边界，电流线与等势线垂直，电流线具有对称轴镜像对称性.这些图形性质符合从顶点流入流出正方形上的电流（势）分布规律.

（3）上半复平面到三角形的保角变换，由文献[6]可知以下变换

把w上半复平面变换为z平面上的三角形，把w复平面上两点 （0，1）变换到z复平面上两点（0，B（α1／π，α2／π） ），3 个 内 角 分 别 为（α1，α2，π-α1-α2），其中B（w，p，q）是不完全贝塔函数.为简单美观起见，我们取正三角形，此时α1＝α2＝π／3，保角变换B（w，1／3，1／3）把点exp（iπ／3）映射到正三角形的中心.把式（3）、式（4）代入式（8），得到正三角形上中心点电荷产生的等势线和电场线如图5所示.

由图5可以看出，越靠近电荷，原点附近的等势线越接近圆形，越靠近边界，等势线越接近于正三角形；电场线垂直于等势线，特别在边界处，电场线垂直于正三角形，电势（场）线具有正三角形对称性.这些图形性质，符合正三角形上点电荷电势的分布规律.

设电流从正三角形一个顶点注入，从另一个顶点流出.把式（5）、式（6）代入式（8），得到正三角形上电流产生的等势线和电场线如图6所示.

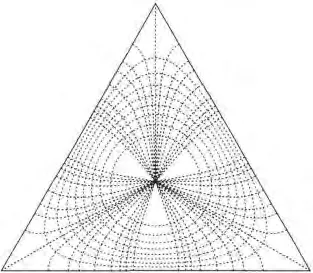
图5 正三角形中心点电荷的等势线和电场线

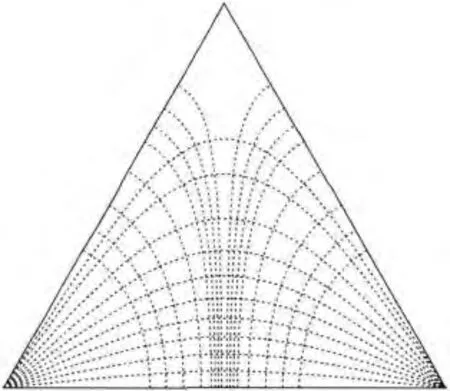
图6 正三角形上电流的等势线和电流线

由图6可以看出，越靠近电流流入（出）点，等势线越接近圆形，在边界处，等势线垂直于边界；越靠近边界，电流线越接近于边界，电流线与等势线垂直，电流线具有对称轴镜像对称性.这些图形性质符合从顶点流入流出正三角形上的电流（势）分布规律.

正方形或正三角形中心电荷所产生的电势（场），由于对称性，也可以用镜像电荷法做.这种情况下，镜像电荷有无穷多个，虽然电势表达式可以明显表示，但这种无穷求和式不大容易得到有限的解析表示，直接用它来数值求值，收敛速度慢，精度不够.文献[2-4]所给的保角变换和反变换，都可以用初等函数（或组合）得到，所以本文的第一种和第二种方法都可以使用.矩形或者三角形的保角变换涉及第一类不完全椭圆积分和不完全贝塔函数，其反变换解析表达式很难求出或者根本没有，就不能用文献[2-4]的方法来求等势线.我们将在另文中继续讨论数值求解保角反变换的例子.

[1]周凌燕，陈钢，郑洁梅.电像法求解线电荷与带有半圆柱凸起的接地平板导体形成的电势和电场[J].大学物理，2013，32（1）：14-16.

[2]王福谦.用保角变换法制作二维第一类格林函数[J].大学物理，2010，29（1）：26-29.

[3]王福谦.求解二维静电场边值问题的一种方法[J].大学物理，2013，32（10）：24-26.

[4]王福谦.复杂形状单连通区域二维第一类格林函数的制作[J].大学物理，2013，32（5）：20-23.

[5]高本庆.椭圆函数及其应用[M].北京：国防工业出版社，1991.

[6]梁昆淼.数学物理方法[M].4版.北京：高等教育出版社，2010.