凸柱体表面缠绕软绳的横向摩擦力的曲率无关性
2015-07-02周国全
周国全
(武汉大学物理科学与技术学院,湖北 武汉 430072)
1 关于圆柱体表面绕绳所受摩擦力的动力学方程问题
当两物体的接触面为平面且存在相对滑动(或相对运动的趋势)时,其相互之间的滑动摩擦力(或最大静摩擦力)与相互之间的正压力成比例,比例系数称为滑动摩擦因素 (最大静摩擦因素),与两接触媒质的材质及表面的粗糙程度有关,并受表面湿润程度与温度等环境因素的影响;在材质一定及表面与环境因素不变的情况下,最大静摩擦因素或滑动摩擦因素是个常量[1-3].对与圆柱体表面接触并有相对运动或运动趋势的物体施加于圆柱表面的摩擦力的研究已屡见于诸文献之中[1-6],如文献[4]讨论了圆棒表面在颗粒物质中受到的纵向静摩擦力的规律;文献[5]则讨论了皮带轮传动装置中的皮带对转轮的横向静摩擦力及主被动轮的动力学方程.
文献[1]~[3]讨论并给出了这一经典的力学问题——在受到横向最大静摩擦力时,圆柱体表面缠绕的柔软轻绳的张力公式
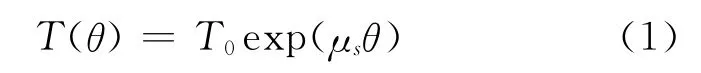
其中,μs为最大静摩擦因数,θ为软绳的绕转角度,而软绳所受的横向最大静摩擦力即为两端的张力T、T0之差.必须指出,文献[2]中的指数衰减律与文献[1]中的指数增长律是彼此一致的,因为摩擦力从绕绳A端到B端的指数增长律,即等价于其从绕绳B端到A端的指数衰减律.但笔者在长期的教学实践中发现,学者们的讨论和研究均局限于圆柱体表面绕绳所受的摩擦力,却忽略了一个重要事实,即凸柱体表面绕绳的张力公式(1)并不局限于圆形截面情形,而与凸柱体横截面的形状无关.本文即专门讨论此问题.对具有任意形状的横向凸截面的柱体,绕绳所受横向最大静摩擦力满足如下公式
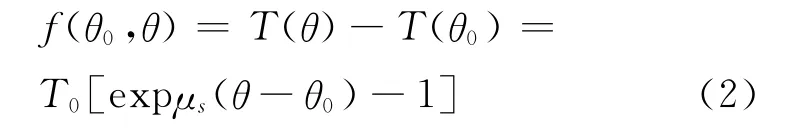

图1 凸柱形直棒上的横向绕绳
图1给出的是横截面为圆形截面情形的示意图.我们考察凸截面的柱体对表面绕绳的摩擦力推导过程,就不难得出软绳与凸柱体表面的横向摩擦力的曲率无关性的结论.
2 软绳与凸柱体表面的横向摩擦力
在凸截面的柱体任一点P处无穷小的一段横向弧元,它实际上重合于P点的曲率圆的张角为dθ(从θ→θ+dθ的元角位移)的一段.设这一小段软绳施加于P处表面的正压力为dN,受到的静摩擦力为df,而在忽略这一小段软绳质量的情况下,如图2所示,由于该无穷小线元受力平衡,因此有如下力平衡方程组


图2 在凸柱体表面P点的弧元上的受力图
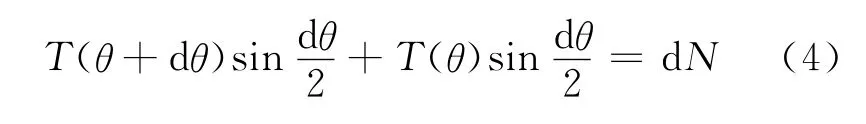
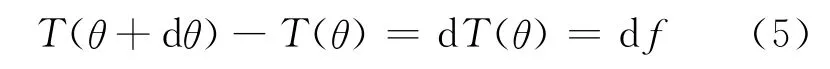
对式(4)中T(θ+dθ)在θ处作泰勒展开并利用近似公式忽略dθ的二次方以上的高阶无穷小项,可得

又一般情形df≤μsdN,当绕绳与柱体间处于最大静摩擦力情形,应有

从式(5)~式(7)可得
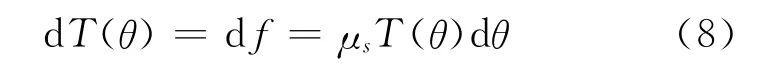
从而有
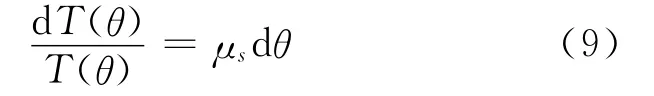
两边积分,注意T(θ0)=T0.当最大静摩擦因数μs为一常数,可得
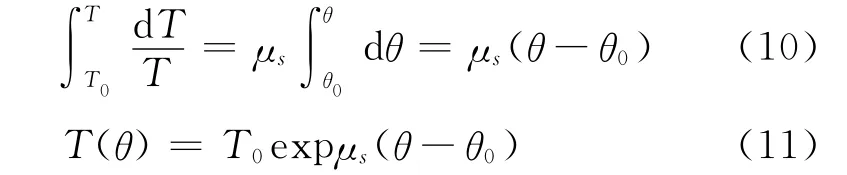
其中,θ-θ0为软绳绕弯曲凸柱体转过的总角度.从式(5)两侧积分可知,总摩擦力等于软绳两端的张力之差

从推导过程可知,柔软的绕绳对弯曲凸柱体表面的横向最大静摩擦力仅与缠绕凸柱体表面的软绳从起始切向方位,向末端切向方位绕转的总角度θ-θ0,以及最大静摩擦因数μs有关,而与凸柱体表面的曲率(或曲率半径)的分布规律无关.证明过程(式(3)~式(12))的合法性,虽然借助了绕绳与凸柱体表面接触点P处元弧(θ→θ+dθ)的曲率圆这一事实,但结果却与曲率k(θ)(或者曲率半径ρ(θ))的具体表达式无关.因此,尽管横截面的周界是一任意平面凸曲线,曲率k(θ)(或者曲率半径ρ(θ))随方位θ而变,曲率圆的圆心位置C也随P点位置不同而变,但式(3)~式(12)总能成立.至此我们证明了前言中的论点.必须指出,前文考虑软绳缠绕凸柱体的最大静摩擦力,式(1)和式(2)及式(7)~式(12)中的μs应理解为最大摩擦因数;而当考虑软绳缠绕并沿凸柱体表面横向滑动时,式(1)和式(2)及式(7)~式(12)中的μs应替换为滑动摩擦因数μk.
在处处满足dθ=0,dN=Tdθ=0的平面特例情形,即对保持平直特性不变(θ=θ0)但有非零摩擦因数的表面,此时公式(1)、式 (2)与式(11)、式(12)依然成立,但最大静摩擦力(或滑动摩擦力)却为零.
3 结语
缠绕于凸柱体表面的软绳所受的横向最大静摩擦力 (或滑动摩擦力)的大小,与凸柱体表面的曲率(曲率半径)的分布无关,即与凸柱体的粗细、形状 (即表面弯曲的程度与方式)无关,而仅与最大静摩擦因数(或滑动摩擦因数),以及软绳在凸柱体表面缠绕的总角度有关,公式(1)和(2)或式(12)和(13)对最大静摩擦因数(或滑动摩擦因数)不变且横截面形状任意的凸柱体表面具有普适性.
[1]梁昆淼.力学[M].北京:高等教育出版社,1978:124-126.
[2]赵凯华,罗蔚英.新概念物理教程:力学[M].1995:72-73.
[3]漆安慎,杜婵英.普通物理学教程:力学[M].1997:318-325.
[4]胡林,杨平,徐亭,等.颗粒物质中圆棒受到的静摩擦力[J].物理学报,2003(4):889-882.
[5]吴伟.简述皮带轮传动装置中皮带两端的张力[J].技术物理教学,2007:(2).
[6]袁乃荣,宋艳芝.如何计算绳索缠绕木桩的最大静摩擦力[J].中学物理,2009:(15).
