Z型舵桨轴系回旋振动计算

舒永东，李祥彪，皮志达

(南京高精船用设备有限公司, 江苏 南京 211103)

Z型舵桨轴系回旋振动计算

舒永东，李祥彪，皮志达

(南京高精船用设备有限公司, 江苏 南京 211103)

采用船舶振动理论对Z型舵桨轴系回旋振动进行理论分析，将Z型舵桨实际系统准确地转化为当量系统，建立回旋振动计算的力学模型，并利用MATLAB计算软件编写回旋振动计算程序，求解相应的振动固有频率和振幅值，使其计算结果符合船级社规范的要求，有利于Z型舵的系列开发。

Z型舵桨；轴系；回旋振动； 船级社规范

0 引言

Z型舵桨轴系是舵桨船舶动力装置中最重要的组成部分，在实际运转中会受到来自内外环境的各种冲击和周期激振力的作用。若这种周期性的持续激振力无法迅速衰减，会破坏Z型舵桨轴系回转的稳态，引起轴系的回旋振动，从而导致轴承松动、尾轴管密封装置损坏、产生漏水、漏油现象，甚至引起轴系断裂，有时也会激起船体尾部的强烈振动[1]。因此，需要针对Z型舵桨轴系回旋振动问题进行深入研究，掌握实用的舵桨振动计算方法，在轴系设计时就能有效地降低Z型舵桨轴系回旋振动幅度，避免对整个Z型舵桨造成破坏。文中采用船舶振动理论对一个Z型舵桨轴系事例进行了回旋振动理论分析，将Z型舵桨实际系统准确地转化为当量系统，建立回旋振动计算的力学模型，并利用MATLAB计算软件，编写回旋振动计算程序，求解相应的振动固有频率和振幅值，使其计算结果符合船级社规范的要求。

1 Z型舵桨推进系统的传动形式及当量模型

1.1Z型舵桨的传动形式

Z型舵桨推进系统轴系主要由主机、高弹性联轴节、短轴组件、万向联轴节、中间轴组件以及Z型舵桨推进系统组成[2]，Z型舵桨推进系统的总布置图如图1所示。

图1 Z型舵桨推进系统总布置图

1.2 回旋振动当量模型

Z型舵桨推进系统内部传动复杂，从输入到输出为Z型传动，包含螺旋伞齿轮、传动轴、立轴、轴承等，准确建立回旋振动当量模型是计算回旋振动的关键，需要将复杂的传动系统转化为合适的当量模型[3]，此模型由刚性匀质圆盘元件、无惯量阻尼元件及无惯量扭转弹簧元件3种基本元件组成。

根据实际系统转换成当量系统的原则，对如图1所示的舵桨推进轴系进行简化处理，并建立回旋振动当量系统模型，如图2所示。

图2 Z型舵桨轴系的回旋振动当量系统模型

2 Z型舵桨推进系统回旋振动理论计算

2.1Z型舵桨推进轴系回旋振动的概述

轴系回旋振动是指螺旋桨处在船尾不均匀的伴流场中，作用在桨叶片上的流体力会对轴系产生弯曲力矩和横向力矩，使得轴在旋转过程中产生周期性弯曲变形的现象，又称为横向振动[1]。

由于回旋振动最重要的激励源——螺旋桨激振力目前仍不能由理论精确得出，作为计算依据的船尾伴流场只能由船模试验求得，但并不是每条船都能提供伴流场的试验数据。因此在实际工程计算中，通常将一次、叶片次正、逆回旋固有频率与轴系的额定转速相比较，共振转速不在0.8～1.2倍额定转速范围内即可满足工程要求[4]，故这里只进行轴系回旋振动的固有频率的计算。采用传递矩阵法进行轴系回旋自由振动计算。

2.2 简化模型的建立

目前一般采用传递矩阵在计算机上进行轴系的回旋振动计算[4]，通常采用集总元件与分布参数元件相结合的简化模型，如图3所示。

图3 螺旋桨——锥齿轮轴段的回旋振动简化模型图

具体的简化原则是[5]：

1) 螺旋桨简化为均质刚性圆盘元件，其质量与转动惯量作为集总参数，应考虑附连水作用；

2) 螺旋桨轴、中间轴按自然分段为等截面均质轴段元件；

3) 轴承按弹性铰支处理；

4) 轴系尾端螺旋桨的边界为自由端。首端边界条件按其首端元件为飞轮、齿轮或高弹分别取为固定端、铰支端和自由端。

在计算回旋振动时，一般不考虑支承元件各向异性，各元件传递矩阵如下：

1)均质刚性圆盘元件的传递矩阵Tp

(1)

式中：j=Jp/Jd；

Jp——考虑附连水影响后螺旋桨的极转动惯量，kg·m2；

Jd——考虑附连水影响后螺旋桨的径向转动惯量，kg·m2；

h=ω/Ω；

ω——推进轴系的旋转角速度，rad/s；

Ω——轴系回旋振动角速度，rad/s；

m——考虑附连水影响后螺旋桨的质量，kg。

2)均质轴段元件的传递矩阵Ts

(2)

当忽略轴段的陀螺效应、剪切变形以及推力影响，传递矩阵各元素为：

T11=T22=T33=T44=C0

T12=T34=C1

T13=T24=C2/EId

T14=C3/EId

T21=T43=PC3

T23=C1/EId

T31=T42=EIdPC2

T32=EIdPC3

T41=EIdPC1

P=ρAΩ2/EId

式中：ρ——轴段材料密度；

A——轴段的横截面积；

E——材料的弹性模量；

Id——轴段截面径向惯性矩；

l——轴段长度。

3)支承伪元件的传递矩阵Tsu

在混合模型中，轴段总是作为均质轴段元件处理的，这时的支承元件是一个无质量，无弹性的伪元件，其传递矩阵为：

(3)

式中：Ke——支承分支的等效线性弹簧刚度。

2.3 轴系回旋自由振动计算

由于齿轮啮合处无法传递弯矩和剪力，根据舵桨推进轴系的基本资料，计算该轴系的回旋振动时分为两段进行考虑：一段为螺旋桨——锥齿轮轴段；一段为两个万向轴中间的中间轴系[6]。

1) 螺旋桨——锥齿轮轴段

螺旋桨——锥齿轮轴段简化处理采用集总参数元件——分布参数元件混合系统模型，将螺旋桨和轴承支承系统作为集总参数元件，将螺旋桨轴和锥齿轮轴模型作为等截面匀质轴段元件处理。根据舵桨推进轴系的基本资料和简化原则，螺旋桨——锥齿轮轴段简化模型几何参数如表1所示。

表1 螺旋桨——锥齿轮轴段简化模型的几何参数表

根据螺旋桨——锥齿轮轴段的简化模型，以及相应的几何参数，利用MATLAB计算得出系统矩阵。然后采用试算频率的方法，计算螺旋桨——锥齿轮轴段的一次正、逆回旋固有频率见表2所示。

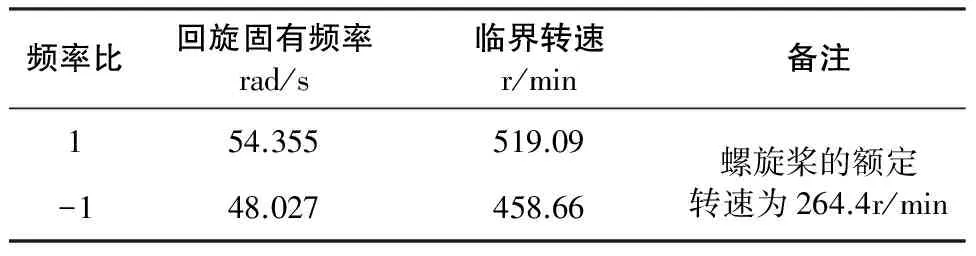
表2 螺旋桨——锥齿轮轴段回旋振动计算结果

根据表2计算结果的分析，螺旋桨——锥齿轮轴段的回旋振动临界转速大于额定转速的1.2倍，符合船规的要求。

2) 中间轴系

中间轴系的简化处理采用集总参数元件——分布参数元件混合系统模型，将轴承支承系统作为集总参数元件，将中间轴和连接法兰模型作为等截面匀质轴段元件处理，考虑到中间轴系两端为万向联轴节，这里将中间轴系两端的边界条件定义为刚性铰支。中间轴系的简化模型如图4所示，简化模型的几何参数如表3所示。

图4 中间轴系的简化模型图

序号名称长度/mm外径/mm内径/mm支承刚度/MN/m1法兰32350002法兰98250003轴段330135004支承00010005轴段1115135006支承00010007轴段1115135008支承00010009轴段11151350010支承000100011轴段3301350012法兰982500013法兰3235000

根据中间轴系的简化模型，以及相应的几何参数，利用MATLAB计算得出中间轴系的系统矩阵。然后采用试算频率的方法，计算中间轴系的一次回旋振动固有频率为129.17 rad/s，临界转速为1 233.57 r/min，中间轴系的额定转速为750 r/min，计算所得中间轴系的回旋振动固有频率大于额定转速264.4 r/min的1.2倍，满足船级社规范要求。

3 结语

在系列Z型舵桨开发设计过程中，利用以上回旋振动分析理论和计算程序计算了几百个事例，并与一些国外公司计算的结果进行了比较，计算的偏差完全在船级社规范要求的范围内。实际计算过的几十条Z型舵桨船舶已经完成了试航，交付使用，轴系运转都比较平稳，没有出现意外情况，所以该Z型舵桨轴系回旋振动计算方法值得推广应用。

[1] 张永根. 船舶振动原因及其减振方法[J]. 江苏船舶，2005，22(3)：16-17.

[2] 盛振邦，刘应中. 船舶原理[M]. 上海：上海交通大学出版社,2004.

[3] 王磊，谢俊超，周瑞平. 大型船舶推进轴系回旋振动特性分析研究[C]. 镇江：第四届全国船舶与海洋工程学术会议论文集，2009：102-106.

[4] 中国船级社. 钢质海船入级规范[S]. 北京：中国船级社，2006.

[5] 中国船级社. 船上振动控制指南[S]. 北京：中国船级社，2000.

[6] 王艳国. 全回转舵桨推进轴系振动计算方法研究[D]. 武汉：武汉理工大学，2011.

Shaft Whirling Vibration Calculation of Z-type Rudder Propeller

SHU Yongdong,LI Xiangbiao,PI Zhida

(Nanjing High Accurate Marine Equipment co., Ltd., Nanjing 211103,China)

In this paper, Shaft whirling vibration of Z-type rudder propeller is analyzed in the theory of ship vibration. The actual system of Z-type rudder propeller is applied to the calculational equivalent system for building the mechanical model of the whirling vibration calculations. And whirling vibration calculation program is compiled with MATLAB software to solve the corresponding natural vibration frequency and amplitude values. The results meet the requirements of classification rules and are in favor of the development of Z-type rudder propeller series.

z-rudder propeller; shaft system; whirling vibration; classification rules

舒永东(1976-)，男，江苏徐州人，高级工程师，硕士，研究方向：船舶设备的设计与制造。

TH123

B

1671-5276(2015)05-0055-03

2014-01-21