高速永磁同步电机转子模态分析与实验研究

2022-02-02丁鸿昌巩玉春张述彪亓航

机床与液压 2022年24期

丁鸿昌，巩玉春，张述彪，亓航

(山东科技大学机械电子工程学院，山东青岛 266590)

0 前言

高速永磁同步电机因功率密度高、体积小、效率高等优点在许多领域得到广泛应用[1]。采用表贴式转子结构的高速永磁电机，通常在永磁体(PM)表面加装高抗拉强度的非导磁护套来抵消永磁体产生的离心力，起保护作用[2]；而定位护套对强度要求不高，采用铝合金材料。部件之间的多种配合方式和接触行为等诸多因素使永磁同步电机转子的模态分析复杂化，导致模态求解难度增加。

高速电机转子模态分析是当前的研究热点，文献[3]中采用包含摩擦效应的接触元件对热装的套筒与空心轴装配体进行了动力学分析，使模态分析结果更接近实验测量值。文献[4-5]中考虑了永磁电机转子装配体各部件间的法向接触刚度和摩擦力的影响，通过有限元仿真软件得到的转子固有频率与测量值吻合良好。目前可查到的文献中对于高速永磁同步电机转子模态的研究主要集中在接触特性对转子模态的影响，而通过等效组件对转子装配体进行模态分析的研究很少。

为简化建模和模态分析过程，对某高速永磁电机转子的低阶模态进行研究，利用等效质量和刚度的方法建立转子的等效模型。通过ANSYS对该模型进行有限元模态分析，并通过LMS锤击实验对仿真结果进行验证，以期为高速永磁同步电机转子模态研究提供参考。

1 系统离散化与运动方程的建立

转子在实际工作过程中会承受联轴器传输的扭转力矩、轴承支承力矩及负载对转子产生的径向冲击力等多种边界条件，但是这些复杂的边界条件无法通过有限元软件精确模拟。文中研究目的是验证简化建模方法的可靠性，所以不需要考虑支撑和约束条件，仅对转子系统进行自由边界条件下的模态分析[6]。

以某高速永磁电机转子为例，转子系统几何模型如图1所示，转子各零部件的材料参数如表1所示。

图1 转子装配体几何模型

表1 转子各零部件材料属性

1.1 有限元法离散化

在转子动力学中，有限元法主要是将转子沿轴向离散为n个弹性轴段单元、n+1个节点，然后对有限个单元的连续系统求解，其中每节点4个自由度。系统离散的单元个数越多计算精度越高，但单元个数过多会耗费大量计算时间，应适当划分单元数量。系统中第i-1至第i+1个节点之间的离散化单元如图2所示。

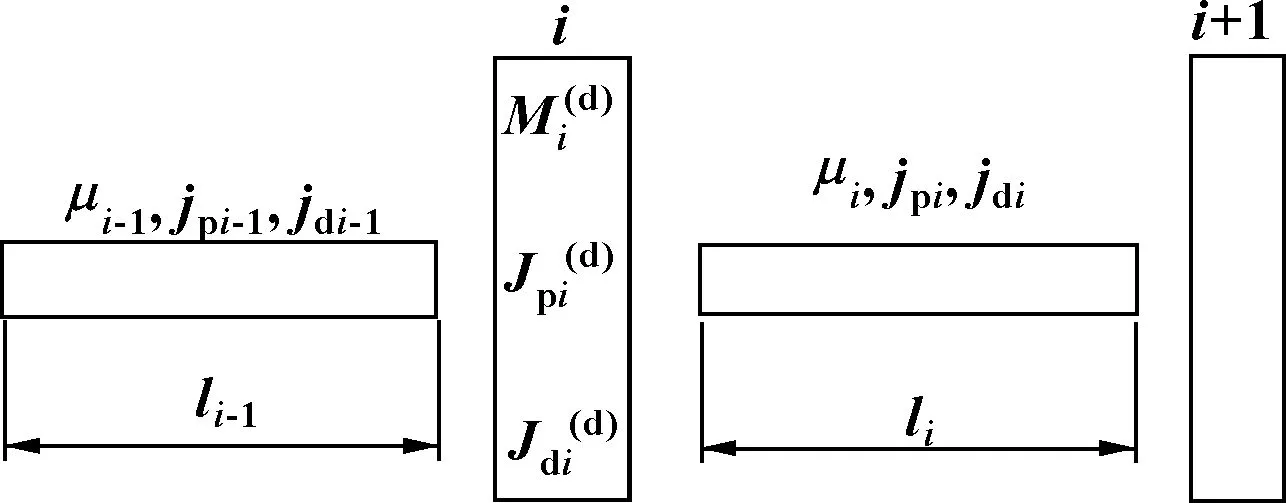
图2 离散化单元模型

1.2 系统运动方程的建立

通常有阻尼柔性转子系统的运动方程可表示为

(1)

(2)

设系统作简谐振动，u(t)=Xsin(ωt)，则式(2)可表示为

(K-Mω2)X=0

(3)

矩阵求解即转化为特征值的求解问题，即

|K-Mω2|=0

(4)

其中:ω为系统固有角频率，令f=ω/2π，f即为系统固有频率;特征向量X为系统主振型。

文献[8]中，通过能量法和插值函数法得出第i个单元的刚度矩阵为

(5)

其中:Ei、Ii、l分别为单元的弹性模量、截面惯性矩和长度。

2 转子系统中转子装配体等效计算

根据机械振动理论中，系统固有频率只与系统自身的质量和刚度有关的原则，若保证轴段的质量和刚度不变，仅改变轴段的几何参数则不会影响系统的固有频率。因此，可通过计算轴段等效质量和刚度，将转子装配体等效为实心转子，进而进行有限元模态分析。转子系统中各部件的关键几何参数如表2所示。

表2 转子系统中各部件的几何参数单位:mm

2.1 模型简化原理及几何参数计算

模型简化原理是通过计算轴段的总质量(等效质量)，得到轴段的等效直径[9]。其中，每个轴段的质量和长度为常数，由于装配轴段的刚度不能被精确计算，等效轴段的材料参数被视为变量。以长度为lz、安装有定位护套的装配轴段为例，其等效原理如图3所示。

图3 配合轴段的等效原理

由图3可以看出：轴段总质量是轴段上部件的质量与轴质量的和，ds是转子实心轴的直径，dh为定位护套的外径，de是轴段的等效直径。轴段总质量，即等效实心轴段的质量me可表示为

me=m+m′

(6)

式中：m、m′分别为轴和定位护套的质量。m和m′可表示为

(7)

其中:ρh为定位护套的材料密度。等效实心轴段的密度ρe与轴的密度ρs相等，式(6)可写为

(de/2)2πρslz=m′+(ds/2)2πρslz

(8)

通过上式，等效轴段的直径de可表示为

(9)

对于由永磁体护套、永磁体、轴组成的轴段，取永磁体和永磁体护套的质量相加作为m′，进行等效计算可得到等效轴段的直径。

代入表3的数据进行数值计算，装有定位护套的轴段等效直径de1为41.4 mm、装有永磁体的轴段等效直径de2为49.6 mm，等效实心转子的几何模型如图4所示。

图4 等效实心转子几何模型

2.2 材料参数的确定

由公式(5)可知，单位长度的轴段抗弯刚度K与轴的截面惯性矩I和材料弹性模量E有关，但各部件之间存在多种影响因素，装配轴段的刚度EI不能被精确计算[10]。由于等效前后轴段的刚度相等，在某集中载荷下，悬臂梁的挠度与刚度的关系可表示为

(10)

其中：ymax为悬臂梁自由端在集中载荷Q下的最大静挠度；Ee和Ie分别为等效轴段的弹性模量和截面惯性矩；l为轴段长度。根据式(10)，可通过有限元分析集中载荷下悬臂轴段的最大挠度，进而推出等效轴段的刚度EeIe。由于每个等效轴段的等效直径已知，等效轴段的截面惯性矩Ie可表示为

(11)

从而得到等效轴段的弹性模量Ee为

(12)

定位护套配合轴段和永磁体配合轴段的长度较小，挠度变化不明显。由于轴段的刚度不受长度的影响，可将配合轴段延长为300 mm，便于观察轴的挠度变化。另外，在装配轴段时，轴的重力对挠度的影响非常小，可忽略不计。在ANSYS中将轴和部件的一个端面设为固定约束，使之成为悬臂状态。为验证轴段刚度不受载荷的影响，依次在轴的自由端沿Y方向施加1 000、2 000、3 000 N的径向载荷，其挠度变化结果如表3所示。

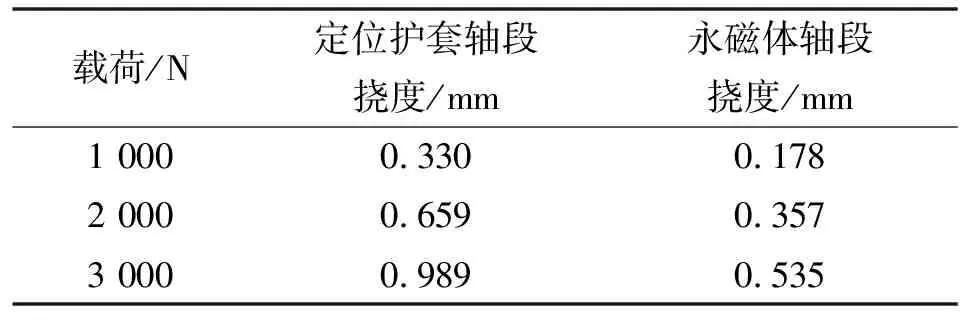
表3 不同载荷下悬臂轴段的变形结果

由表3可知:载荷与挠度成正比，因此载荷的变化不会影响轴段的刚度。径向载荷为1 000 N时2个轴段的变形如图5所示，可知：有定位护套的轴段，自由端在Y方向的最大挠度为0.33 mm；有永磁体的轴段，自由端最大挠度为0.178 mm。

图5 悬臂轴段的挠度

将公式(11)代入公式(12)并进行代数计算，得到有定位护套的轴段等效后轴段的弹性模量为192.4 GPa、有永磁体的轴段等效后轴段的弹性模量为170.2 GPa。

3 等效实心转子ANSYS模态分析

ANSYS是转子动力学研究常用的工具，且对单一结构进行模态分析的结果准确可靠，因此被用于验证该等效模型的可靠性。由于各等效轴段材料属性不同，在SolidWorks中分别建立各等效轴段及其他轴段的三维模型，各轴段以同轴心和面-面重合的方式进行配合，以便进行后续材料属性的设置。

将等效实心转子的3D模型导入ANSYS，根据表1和第2.2节中计算的等效轴段弹性模量设置每个轴段的材料属性，各轴段的密度均为7 850 kg/m3，轴段之间的轴向接触面均采用Bonded接触，以模拟实心轴的整体结构。等效实心转子被划分为37 549个网格单元、132 469个节点，有限元模型如图6所示。

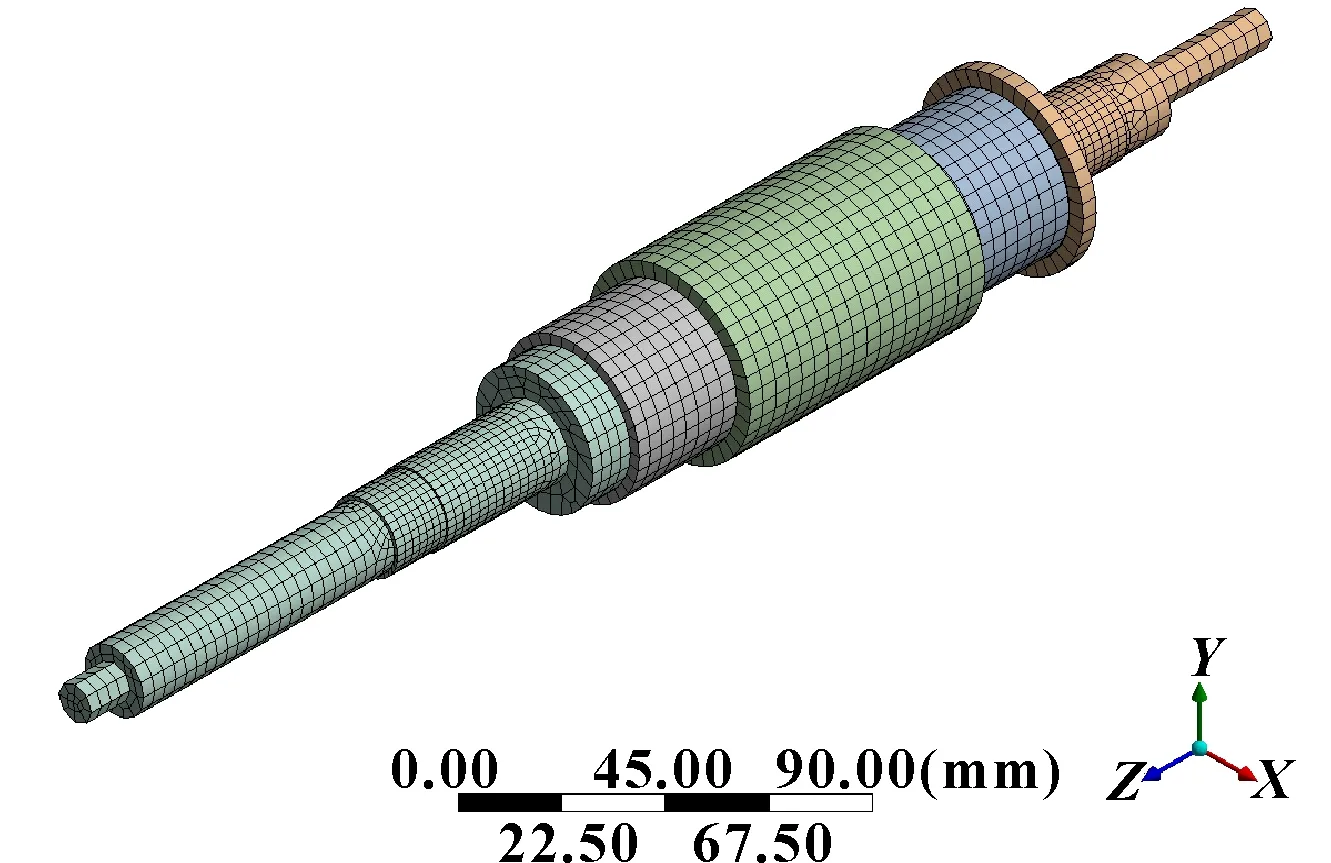
图6 等效实心转子有限元模型

在转子动力学中，低阶固有频率对转子的振动起主要作用，因此只分析转子的前10阶模态[10]。在分析结果中,由于前6阶模态未出现明显变形，且固有频率接近于0，可忽略不计。等效实心转子的1阶和2阶固有频率分别为1 165.8、3 421 Hz，对应的前2阶弯曲振型如图7所示。

图7 等效实心转子模态振型

从图7可以看出:等效实心转子的1阶弯曲振型沿Z轴只发生了1次弯曲，2阶弯曲振型沿Z轴发生了2次弯曲，且弯曲主要发生在两端的轴颈处。

4 实验验证

4.1 平台搭建

锤击法模态实验是准确获取机械结构模态频率的主要手段[11]。LMS锤击法模态实验平台如图8所示，实验装置包括支撑架、弹性绳、转子、激励锤、加速度传感器、LMS振动实验分析系统和计算机等。为模拟转子的自由-自由边界条件，用弹性绳将转子水平悬挂在支撑架上。将加速度传感器分别固定在转子表面3个互相垂直的方向，并与振动分析系统的信号输入端口连接。