基于粗糙集改进算法的神经网络故障诊断方法

楼宇舟，涂俊翔

(福州大学 机械工程及自动化学院，福建 福州 350000)

基于粗糙集改进算法的神经网络故障诊断方法

楼宇舟，涂俊翔

(福州大学 机械工程及自动化学院，福建 福州 350000)

针对BP神经网络在实际工程应用中受到大量冗余信息的制约，以及基于信息熵的属性离散方法的阈值选取具有主观性的缺点，提出了改进的基于信息熵的粗糙集连续属性离散化算法。该算法将Naivescaler离散化算法和信息熵离散化方法相结合，减少了离散化算法中候选离散点的数量；基于粗糙集约简信息决策表，有效解决了BP神经网络训练样本过于庞大的问题；并通过改进的离散化算法对属性约简后数据进行分类，将分类后的数据运用到神经网络运算中，进一步缩短了神经网络的运算时间。通过实例分析表明，该方法具有很好的故障诊断效果，并有效提高了诊断效率。

粗糙集；信息熵；约简；离散化；神经网络；故障诊断

随着科技进步的发展，现代工业设备大型化、复杂化、自动化的程度越来越高，为保证各种设备安全和高效地运行，智能故障诊断技术应运而生。其中，基于神经网络的故障诊断方法已进入实用阶段，实际应用有卫星姿态测量系统故障诊断、船舶柴油机故障诊断、航天飞机发动机故障诊断等。但在工程实践中，往往存在所选的特征参数过多，使得神经网络规模过于庞大、结构过于复杂、算法收敛速度过慢、精度低等问题，影响了故障诊断的可靠性和实用性[1-2]。

Pawlak教授提出的粗糙集理论(RST)，具有无需提供任何先验信息，直接对已知信息进行分析处理，删除冗余信息的优势[3]。在设备故障诊断中，将粗糙集理论与神经网络相结合，可以更有针对性地对已有信息进行分析处理，删除其中冗余信息，从而降低数据的规模，克服了单一神经网络的拓扑结构规模大，计算复杂，无法实现实时故障诊断的局限性[4-5]。由于粗糙集理论只能处理离散型数据，而故障信息绝大多数是连续性的，因此需要对故障信息进行离散化处理，但现阶段还没有一种较理想的离散化方法可以适用于多领域的离散化需求，因此在不同领域的故障诊断中需要应用各种不同的离散化方法。

现改进了基于信息熵的粗糙集离散化算法，并将粗糙集理论，BP人工神经网络技术结合起来，提出了一种基于粗糙集和神经网络的故障诊断方法。实验结果表明，该方法相对于基于单一神经网络的故障诊断方法，具有减小神经网络规模，加快收敛时间等优点。

1 粗糙集理论

1.1 知识与不可分辨关系

a) 知识表达系统和决策系统

b) 不可分辨关系

不可分辨关系是粗糙集理论中非常重要的概念，是用来表达由于缺乏一定的知识而不能将已知信息系统中的某些对象区别开，其实质是一个等价关系。

定义2：设S=(U,A,V,f)为一个信息系统，R是U上的一族等价关系，若P⊆R,且P≠Φ,则∩P也是一个等价关系，称其为P上的一个不可分辨关系，用ind(P)来表示，即：

ind(P)={(x,y)∈U×U:f(x,a)=f(y,a),a⊆P}

1.2 粗糙集的上近似、下近似

当集合X能表示成基本等价类组成的并集时，则称集合X是R可精确定义的，称作R的精确集；否则，集合X是R不可精确定义的，称作R的非精确集或R的粗糙集。对于集合的粗糙集可利用以下2个精确集来描述，即上近似和下近似。

定义3：X关于R的下近似为：

定义4：X关于R的上近似为：

1.3 属性约简与核

在决策表中，往往具有很多不同的属性，这些属性对于知识的决策具有不同的重要性，有些属性对于决策起到决定性作用，而有些属性却是可有可无的。在粗糙集理论中，针对信息系统，在保持信息系统分类能力不变的情况下，通过消除冗余属性和冗余样本，最终得到信息系统的分类或者决策规则的方法称为知识约简。

2 离散化算法和信息熵

2.1 离散化算法

由于粗糙集理论只能处理离散型数据，而实验中获得的数据大多往往是连续的，因此实现属性值的离散化是应用粗糙集理论进行分析和处理的前提。合适的离散化算法，不仅可以大大减少信息的大小，还可以提高属性值分类的准确性[7]。

2.2 信息熵

信息熵是信息源X不确定性的量度。每个信息源都有且只有一个信息熵，不同的信息源，由于其统计特征的不同，所得的熵也不同。Shannon把信息熵定义为随机离散事件的出现概率，即信息源的平均信息量[8]。

(1)

其中：pi表示时间xi发生的先验概率，对数取以2为底，而当某个pi为零时，则理解为0·log0=0。

3 BP神经网络结构

BP学习理论最早在1974年由Webos提出，1985年发展成了BP网络学习算法。BP神经网络是指具有非线性传递函数的神经元的前馈网络，并通过误差反向传播来调整各层神经元之间的权值。该网络不仅具有输入层，输出层，同时还具有一层或者多层的隐含层，其中同层之间不能相互影响[9,10]。

小麦区域试验采用随机区组法，3次重复。小区行距0.15米，10行区，小区面积15平方米，各品种间间隔0.3米。并设不少于6行的保护区。全区收获计产，计算增（减）产百分率。

图1 三层BP神经网络结构

4 故障诊断方法

4.1 基于信息熵的粗糙集属性离散化方法的候选离散点的选择

决策表S=(U,A,V,f)，对于每个属性按照属性值由大到小进行排序，计算每两相邻属性值的平均值作为候选断点。

4.2 改进的基于信息熵的粗糙集属性离散化方法

决策表S=(U,A,V,f)如前文所述，候选离散点的个数近似等于每个属性的属性值个数，候选离散点数量过多，会大大影响后续应用粗糙集理论进行分类的效率。

在原有基于信息熵的离散化算法的基础上引入Naivescaler离散化算法，对于每个属性按照属性值由大到小进行排序；依次判断两相邻实例的属性值和决策值，如果两者都不同，则将两属性值的平均值作为候选断点c，B为候选断点值集；若两者有一个相同，则不取两属性值的平均值作为候选断点；同时计K为属性的候选断点个数，与原方法相比，大大减少候选断点的数量。

(2)

(3)

(4)

(5)

(6)

(7)

同时，由于基于信息熵的离散化算法对于阈值选取具有很强的主观性，往往需要研究者通过经验来判断选取阈值的大小。针对这一缺点，文中提出了选取阈值为H(X)/K，当离散前后断点信息熵的差值小于H(X)/K时，停止离散，避免了选取阈值时由于人为选取带来的主观性问题。

综上所述，改进的基于信息熵离散化算法如下：

1) 对于每个属性按照属性值由大到小进行排序。依次判断两相邻实例的属性值和决策值，如果两者都不同，则将两属性值的平均值作为候选断点值，B为候选断点值集，同时计K为属性的候选断点个数，P为已选取断点集；

2)P=Φ；L={U}；H=H(U)；H1=H；

3) 对每个c∈B,计算H(c,L)；H2=min(H(c,L));

4) 若H1-H2≤H/K，则结束；

5) 令当H(c，L)=H2断点为cmin，将其加入到P中，B=B-{cmin}；

6) 对于所有X∈L，若cmin将X分为两部分，记为X1、X2，则在L中去掉X并将等价类X1、X2加入到L中；

7) 如果L中各个等价类中的实例都具有相同的决

策，则结束；否则转到步4。

4.2BP神经网络故障诊断模型的构建

先将实验测点的原始数据进行离散化分类处理，然后将结果输入到神经网络进行训练和预测，充分发挥了离散化算法的分类功能，同时减少了神经网络的运算时间。故障诊断系统流程图见图2。

图2 故障诊断系统流程图

5 应用实例

UCI(university of california irvine)机器学习标准数据集是加州大学欧文分校提出的用于机器学习的常用标准测试数据集，是模式识别的公用数据，而故障诊断的实质是数据分类与模式识别。因此，采用的数据取自UCI机器学习标准数据集中的wine数据集，数据集共有178组数据，3个状态，13个条件属性，构建知识系统，其中：

S=(U,A,V,f)，U={x1,x2…x178}，A=C∪D,C∩D=Φ，C={c1,c2…c13}，D={d1,d2,d3}。所构建的故障诊断决策表如表1，属性A-M为条件属性，N为决策属性1[12-13]。

表1 原始数据决策表

每10个样本选取1个作为测试样本，剩余作为训练样本。若使用基于信息熵的粗糙集属性离散化方法，对于属性D则得到近160个候选离散点；当使用改进的基于信息熵的粗糙集属性离散化方法时，获取的候选离散点为29个，大大减少了候选离散点的数量，有效缩短了后续离散化计算的时间。

表2为对训练数据进行基于改进的信息熵的离散化算法处理后所获得的决策表。

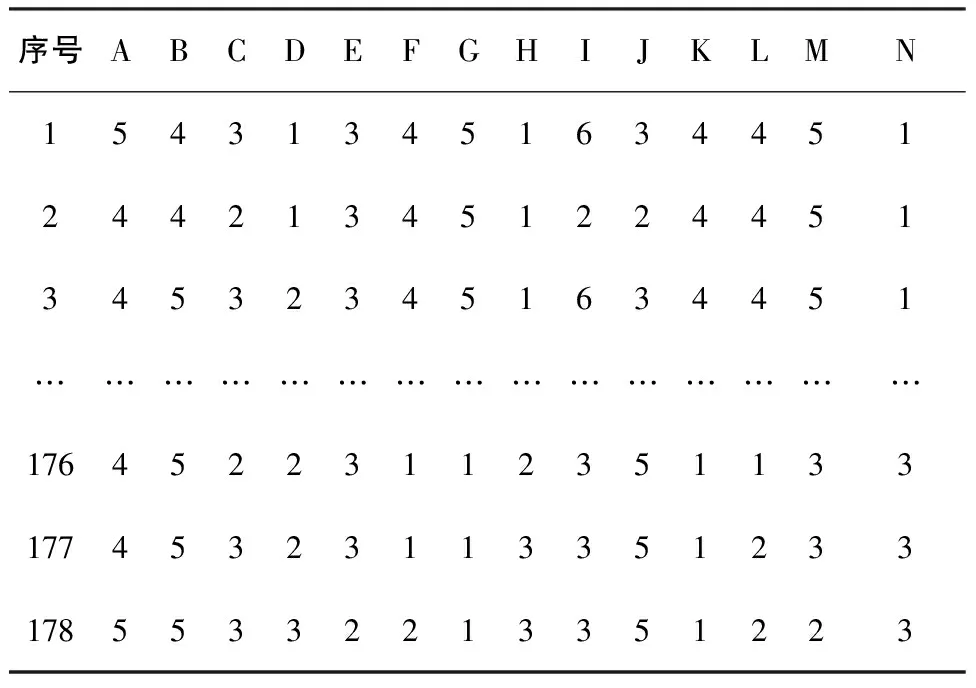
表2 离散化后数据决策表

按照粗糙集理论进行属性约简算法进行约简，利用粗糙集软件Rosetta，可得属性约简结果为{c2,c3,c6,c8,c10,c11}，选取{c2,c3,c6,c8,c10,c11}作为输入节点构建BP神经网络；通过纵向约简将各属性值相同的样本删去，决策表可得剩余125组数据；由于决策属性为3种，因此输出节点为3个，{1,0,0}为1，{0,1,0}为2，{0,0,1}为3；隐含层节点为400个，神经网络程序为[14]：

net=newelm( minmax(p),[400,3],{'tansig','purelin'});

net.trainParam.show=50;

net.trainParam.epochs=10000; %训练次数设置

net.trainParam.goal=1e-3; %训练所要达到的精度

net.trainParam.lr=0.05; %学习速率

图3为未使用粗糙集理论进行数据预处理的神经网络训练误差曲线，图4为使用粗糙集理论进行数据预处理的神经网络训练误差曲线。

图3 未使用粗糙集理论误差精度曲线

图4 使用粗糙集理论后的误差精度曲线

对测试样本进行预测，结果见表3。

表3 预测样本决策表

符合UCI机器学习标准数据集提供的数据，对故障类型的认定完全一致；同时在诊断精度一致的情况下收敛次数由单一神经网络的6 372次减少到2 003次，收敛速度大大增加。因此，提出的故障诊断模型具有很好的可行性与有效性。

6 结语

将粗糙集和BP神经网络的优点结合起来，建立了基于粗糙集和BP神经网络的故障诊断模型，并改进基于信息熵的属性离散算法，避免该算法需要人为主观设定阈值的不足，同时优化其候选断点的个数，如属性D，候选离散点由160点降至29点，加快了后续属性离散的速度。通过测试结果表明，基于粗糙集和BP神经网络的故障诊断方法与单一运用BP神经网络相比，在保证训练精度的同时，收敛次数从6 372次降到了2 003次，明显提高了训练速度，故障诊断效率较高，具有较高的工程实用性。

[1] 王彪，吴昊，宋永刚，等. 粗糙集和模糊集的研究及应用[M]. 北京: 电子工业出版社, 2008: 2-10.

[2] 于学军，程博. 基于BP神经网络的工作量估算模型[J]. 计算机学报, 2012, 39(10): 97-100.

[3] 张文修，吴伟志，梁吉业. 粗糙集理论与方法[M]. 北京:科学出版社, 2001: 1-30.

[4] 沈晨鸣. 基于粗糙集理论多知识库的知识发现[J]. 机械制造与自动化, 2007, 36(2): 8-13.

[5] 庞继红，张根保，周宏明，等. 基于粗糙集的数控机床精度设计质量特性反向映射研究[J]. 机械工程学报, 2012, 48(5): 101-107.

[6] 王文逾. 基于粗糙集的分体错位式动态汽车称重系统研究[J]. 太原理工大学学报，2011, 42(6): 639-641.

[7] Lukasz A, Kurgan, Krzysztof J. Cios. CAIM Discretization Algorithm[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(2): 145-153.

[8] Ajay Kumar, David Zhang. Hand-Geometry Recognition Using Entropy-Based Discretization[J]. IEEE Transactions on Information Forensics and Security, 2007, 2(2): 181-187.

[9] 张本国，李强，王葛，等. 基于改进BP神经网络的连铸漏钢预报[J]. 中国机械工程, 2012, 23(2): 204-207.

[10] W. ERIC WONG, YU QI. BP neutral network-based effective fault localization [J]. International journal of software engineering and knowledge engineering. 2009, 19(4): 573-597.

[11] 谢宏，程浩忠，牛东晓. 基于信息熵的粗糙集连续属性离散化算法[J]. 计算机学报, 2005, 28(9): 1570-1574.

[12] 胡平，彭纪奎. 粗糙集-遗传神经网络在挖掘机故障诊断中的应用研究[J]. 微电子学与计算机, 2011, 28(3): 55-58.

[13] 何勇，李增芳. 智能化故障诊断技术的研究与应用[J]. 浙江大学学报(农业与生命科学版), 2003, 29(2): 119-124.

[14] 傅荟璇，赵红，等. MATLAB神经网络应用设计[M]. 北京：机械工程出版社，2010: 136-139.

Research on Fault Diagnosis Method Based on Improved Algorithm in Rough Set

LOU Yuzhou，TU Junxiang

(School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350000, China)

In view of BP neural network in practical engineering applications constrained by the large number of redundant information and the subjectivity of attribute discretization method based on information entropy in threshold selection, an improved discretization algorithm for continuous attribute in rough set based on information entropy is proposed. The Naivescaler algorithm is combined with information entropy discretization method in this algorithm and it is used to greatly reduces the number of candidate discretization points and effectively handles the big sample for BP neural network training. The neural network computation time is further reduced by classifying the data set with reduced attributes and applying the classified data to the neural network. The practical application of the method proves that it has better performance and efficiency for fault diagnosis.

rough set; information entropy; reduction; discretization; neural network; fault diagnosis

福建省自然科学基金(2012J01208)

楼宇舟(1988-)，男，硕士，主要研究方向为智能信息处理、故障信息诊断。

TP183

B

1671-5276(2015)05-0204-05

2014-03-21