在反函数法求函数值域时应注意的一个问题

文/夏金亮

在反函数法求函数值域时应注意的一个问题

文/夏金亮

对于函数值域问题的讨论是初等数学中最基本也是最重要的问题。其重要之处在于这类问题研究的是函数基本概念，它与各类重要函数、反函数、函数的单调性、不等式、最值和导数等内容有着密切的联系。对认知函数以及后面的相关内容的学习有着非凡的意义，所以求函数的值域也成为各类考试的热门知识点。本文将对求函数值域时使用反函数法应注意的问题作出讨论。

反函数法;函数;值域

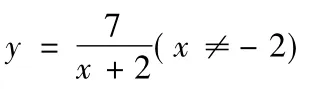
这个结果虽然正确，但是其简答的方法却又逻辑上的错误。

那么对于例1使用上述方法解答的结果为什么会正确呢?在什么情况下使反函数表达式有意义的一切x值的集合恰好是原函数的值域?对于这个问题，编者认为下面的定理对其作出了完整的解释:

设函数y=f(x)的定义域A是使表达式y=f(x)有意义的一切x的值的集合，其反函数的表达式为y=g(x)，如果使表达式y= g(x)有意义的一切x值的集合为B0值域为A0，且存在g:B0→A0是一一映射，那么B0就是原函数y=f(x)的值域B。

证明:对于任意的b∈B，有a∈A，使得f(a)=b

∵f有逆映射g，故有g(b)=a，∴b∈B0，即有B⊆B0。

现任取b0∈B0，则存在a0使得g(b0)=a0，由于g:B0→A0是一一映射，其逆映射确定的函数应为y=f(x)，(x∈A0)，故有f(a0)=b0，其中a0∈A0，由于A是使表达式y=f(x)有意义的一切x的值的集合，∴A0⊆A，∴a0∈A，于是由f(a0)=b0知b0∈B

∴B⊆B0

综上所述知B=B0，证毕。现在我们回头看看前面所提到的例1，例2两个小题:

因此对于利用反函数求函数值域这一方法必须在学生对于函数一一对应关系以及逆映射等概念有充分理解掌握的前提下进行讲解，并对于那些类型函数值域求值不适合使用此反函数求值法给出例题解说。另外求原函数的反函数时，同学们往往容易出现偏差，而影响求原函数的值域，这也是要十分注意的一个问题。

由上述例题可见，在使用求反函数的定义域来求原函数的值域时，对于原函数的定义域的多样性我们必须要有清晰的认知和理解，而准确无误的求出原函数的反函数是使用反函数法求原函数值域的关键问题。

(作者单位:凯里学院)