柯西不等式变式的应用

文/覃发岗 宁纪献

柯西不等式变式的应用

文/覃发岗 宁纪献

对柯西不等式基本形式、推论作了归纳，然后给出了其推论的应用。

不等式;应用;柯西不等式

1.引言

柯西不等式是数学中一个非常重要的不等式，它结构对称和谐，具有较强的应用性，深受人们的喜爱。它的推论也比较多，本文主要介绍其四个推论及其应用。

2.柯西不等式的变式

2.1 柯西不等式的基本形式［1］

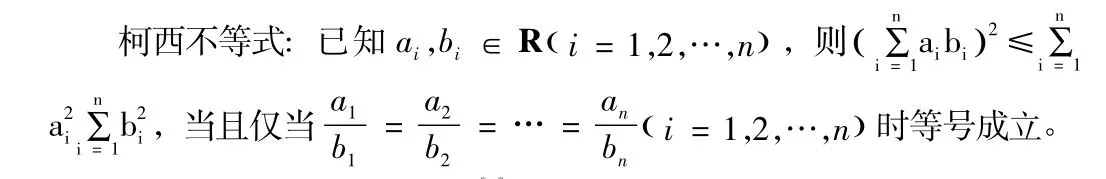
2.2 柯西不等式的变式［2］

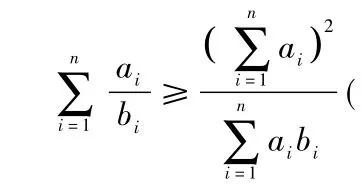
变式二

变式五

将柯西不等式两边开平方根即得。

3.应用柯西不等式的变式

3.1 应用变式一

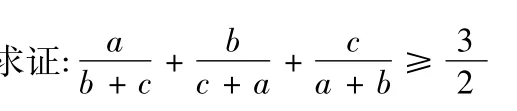
证明由变式一可得，

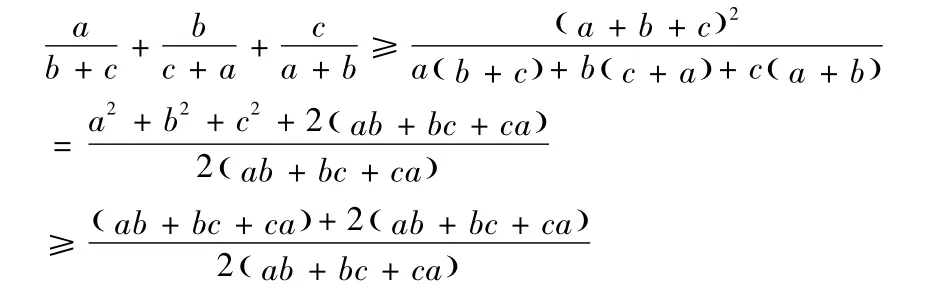
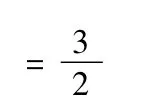
故原不等式成立。

3.2 应用变式二

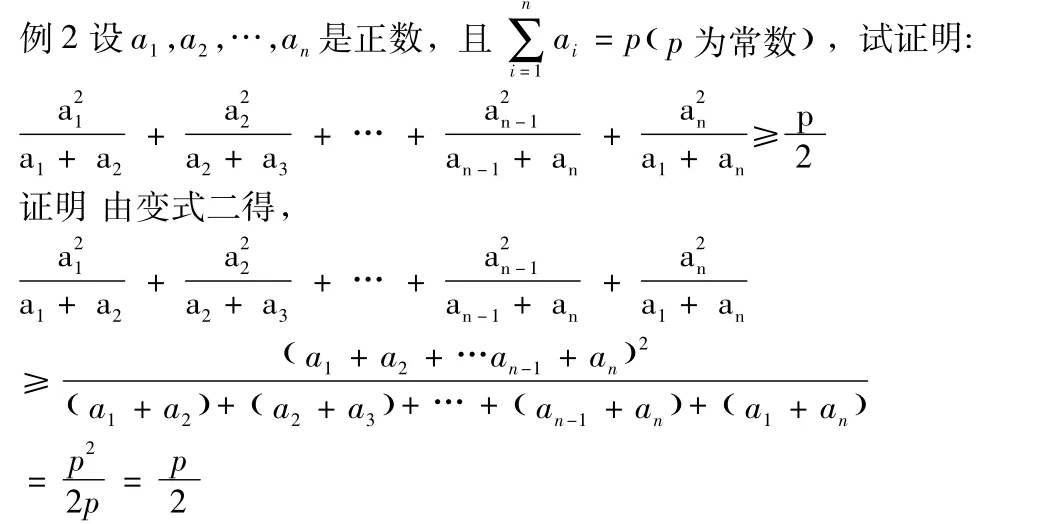
故原不等式得证。

3.3 应用变式三

例3已知x+2y+3z+4u+5v=30，求W=x2+2y2+3z2+4u2+5v2的最小值。

解:由变式三得，

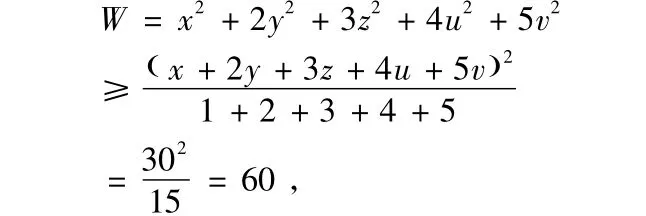
当且仅当x=y=z=u=v即x=y=z=u=v=2时等号成立，故W的最小值为60。

3.4 应用变式四

例4已知a，b，c，d∈R+，且a+b+c+d=1，求证:

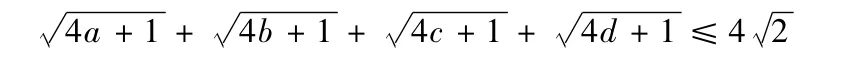
证明可利用变式四，令

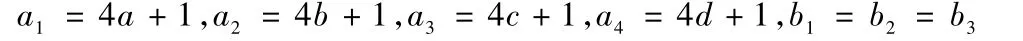
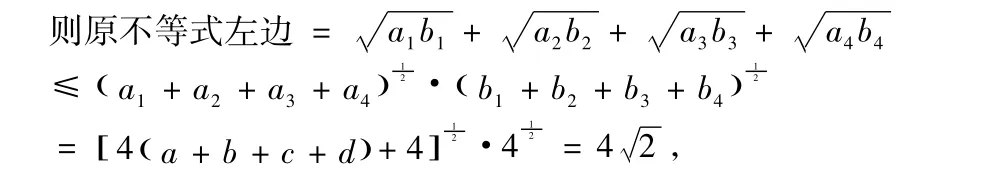
故原不等式成立。

(作者单位:云南大学数学系)

［1］谢跃进.柯西不等式应用探讨［J］.铜仁职业技术学报(自然科学版).2008，6(6):59.

［2］王晓凤.对柯西不等式的探讨［J］.通化师范学院报，2006，27(2):23－25.

This paper introduces the Cauchy inequality from its basic form，deformation.Then reveals their application in inequality by series examples.

Inequality;Application;Cauchy Inequality.