论八年级数学中多项式因式分解的方法

云南省玉溪市峨山县小街中学 杨东笑

在初中数学中，因式分解是一个十分重要的概念，它是整式乘法的逆过程，是代数式恒等变形的一个重要组成部分，也是处理数学问题的重要手段和工具，在代数式的运算、解方程等方面有极其广泛的运用。

一、因式分解的定义

把一个多项式化为几个最简整式的乘积的形式，这种变形叫做把这个多项式因式分解（也叫作分解因式）。

因式分解是初中数学中最重要的恒等变形之一，它被广泛地应用于初等数学之中，是我们解决许多数学问题的有力工具。学习它，既可以复习整式四则运算，又为学习分式打好基础；既可以培养学生的观察、思维发展性、运算能力，又可以提高学生综合分析和解决问题的能力。

二、因式分解的基本方法

1.提公因式法

如果一个多项式的各项有公因式，可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法。

例题：分解因式bm-am+cm

分析：在多项式bm-am+cm中，每个单项式都含有字母m，故提出m就可以了。

解： bm-am+cm

= m(b-a+c)

2.公式法

如果把乘法公式反过来，就可以把某些多项式分解因式，这种方法叫公式法。

公式主要有以下三个。

例题：分解因式 4a2-9b2

分析：∵4a2=(2a)2，9b2=(3b)2，只要把2a和3b看作平方差公式中的a和b即可。

解： 4a2-9b2

= (2a)2-(3b)2

= (2a+3b)(2a-3b)

3.分组分解法

能分组分解的多项式有四项或大于四项，一般的分组分解有两种形式：二二分法，三一分法。

例题：把多项式ax+ay+bx+by分解因式

分析：通过观察、分析，发现此题应用二二分法：把ax和ay分一组，bx和by分一组，利用乘法分配律，两两相配。

解： ax+ay+bx+by

= a(x+y)+b(x+y)

= (a+b)(x+y)

4.十字相乘法

十字相乘法简单来讲就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。

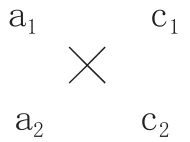
例题：把多项式x2+2x-15分解因式

分析：通过观察，此题采用十字相乘法就可以了。

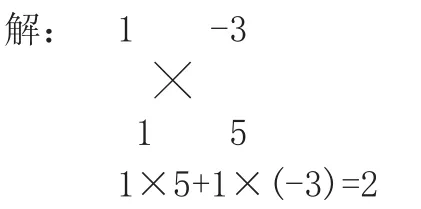
所以x+2x-15=(x-3)(x+5)。

5.拆项、添项法

因式分解是多项式乘法的逆运算。在多项式乘法运算时，整理、化简常将几个同类项合并为一项，或将两个仅符号相反的同类项相互抵消为零。在对某些多项式分解因式时，需要恢复那些被合并或相互抵消的项，即把多项式中的某一项拆成两项或多项，或者在多项式中添上两个仅符合相反的项，前者称为拆项，后者称为添项。拆项、添项的目的是使多项式能用分组分解法进行因式分解。

例题：把m2-6m+8 分解因式

分析：本题有两种方法：既可以将8拆成9-1，也可以将-6m拆成-2m-4m.

解法1： m²-6m+8

= m²-6m+9-1

= (m-3)²-1²

=（m-3+1）(m-3-1)

= (m-2)(m-4)

解法2： m²-6m+8

= m²-2m-4m+8

= m(m-2)-4(m-2)

= (m-2)(m-4)

6.配方法

对于某些不能利用公式法的多项式，可以将其配成一个完全平方式，然后再利用平方差公式，就能将其因式分解，这种方法叫配方法。属于拆项、补项法的一种特殊情况。也要注意必须在与原多项式相等的原则下进行变形。

例题：把多项式x²+6x-7分解因式

解： x²+6x-7

= x²+6x+9-16

= (x+3)2-42

=（x+3+4）(x+3-4)

= (x+7)(x-1)

三、因式分解的一般步骤

一是如果多项式的各项有公因式，那么先提公因式；

二是如果各项没有公因式，那么可尝试运用公式、十字相乘法来分解；

三是如果用上述方法不能分解，那么可以尝试用分组、拆项、添项法来分解；

四是分解因式，必须进行到每一个多项式因式都不能再分解为止。

也可以用一句话来概括：“先看有无公因式，再看能否套公式，十字相乘试一试，分组分解要合适。”

四、在因式分解中应注意的问题

第一，因式分解中应注意的几个问题，可用四句话概括如下：首项有负常提负，各项有“公”先提“公”，某项提出莫漏1，括号里面分到“底”。

第二，考试时应注意，在没有说明化到实数时，一般只化到有理数就够了，有说明实数的话，一般就要化到实数。