推波板制造双频波数值模拟
2015-06-29李海涛
李海涛
【摘要】:本文应用软件为FLUENT流体分析软件,控制方程为连续性方程和Navier-Stokes方程。应用GAMBIT建立数值波浪水槽模型并对其划分网格。基于标准RNG 湍流模型和VOF自由液面捕捉方法,利用FLUENT的二次开发编写源程序,赋予前边界造波功能,以及后边界数值消波功能,采用动网格来实现推波板单频造波。其与实际物理实验造波原理相符。并在此基础上,以stokes有限振幅波理论为基本理论,运用二阶双色波的推波板运动方程实现非线性双频波造波数值模拟。
【关键词】:Fluent、动网格、推波板、造波、双频波
中图分类号:TP31 文献标识码:A 文章编号:1672-3791(2015)05(c)-0000-00
中国的经济发展其不开海洋的开发利用,目前各个国家也都十分重视海洋资源的利用。而波浪运动在海洋能量资源中起着举足轻重的作用,它既可以对人类生命财产造成极大威胁,又可以作为清洁能源改变人类的生活。因此对于合理利用波浪的研究成为一直以来人们密切关注的话题。波浪是一种规律性、周期性起伏运动,受风向及大气压变化等因素的影响。但随着海洋科学技术和计算机技术的快速发展,相信人们可以通过更好的了解利用波浪来造福人类。
1、 数学模型和数值方法
推波板造波法是物理模型实验中常使用的方法,应用在数值模拟中,即为数值水槽设置动边界即可。根据线型造波机理论,往复周期运动的推波板可以制造出单频波:
(1)
其中: 为推波板运动的角频率,同时也为所造波的角频率, ; 为所造波的波数, ; 为推波板冲程; 为水深。
根据公式(),我们可以推出,为制造出波高 的单频波,推波板的运动为:
(2)
(3)
其中: 为推波板的运动速度。
本文设定数值水槽左边的固壁边界为动边界。当动边界的运动幅度超过一个网格时,必须采用非结构网格,以此能够实现网格重构。
以上为推波板造波法制造单频波的参数设定。对于物理实验中模拟不规则波,往常人们通常采用线性叠加的方法。将海浪视为一个平稳随机的过程,它可由多个(理论上应为无限多个)不同周期和不同随机初相位的余弦波叠加而成[1]。但这种方法没有考虑不同频率的波之间的相互作用。Sch?ffer[2]以stokes有限振幅波理论为基础,提出不规则波的二阶造波理论,又在此基础上,发展了多向波的二阶造波理论[3]。本文即运用Sch?ffer的二阶造波理论,得出能够造出二阶双频波的推波板运动方程[4],在此基础上编写UDF。
2、 结果对比
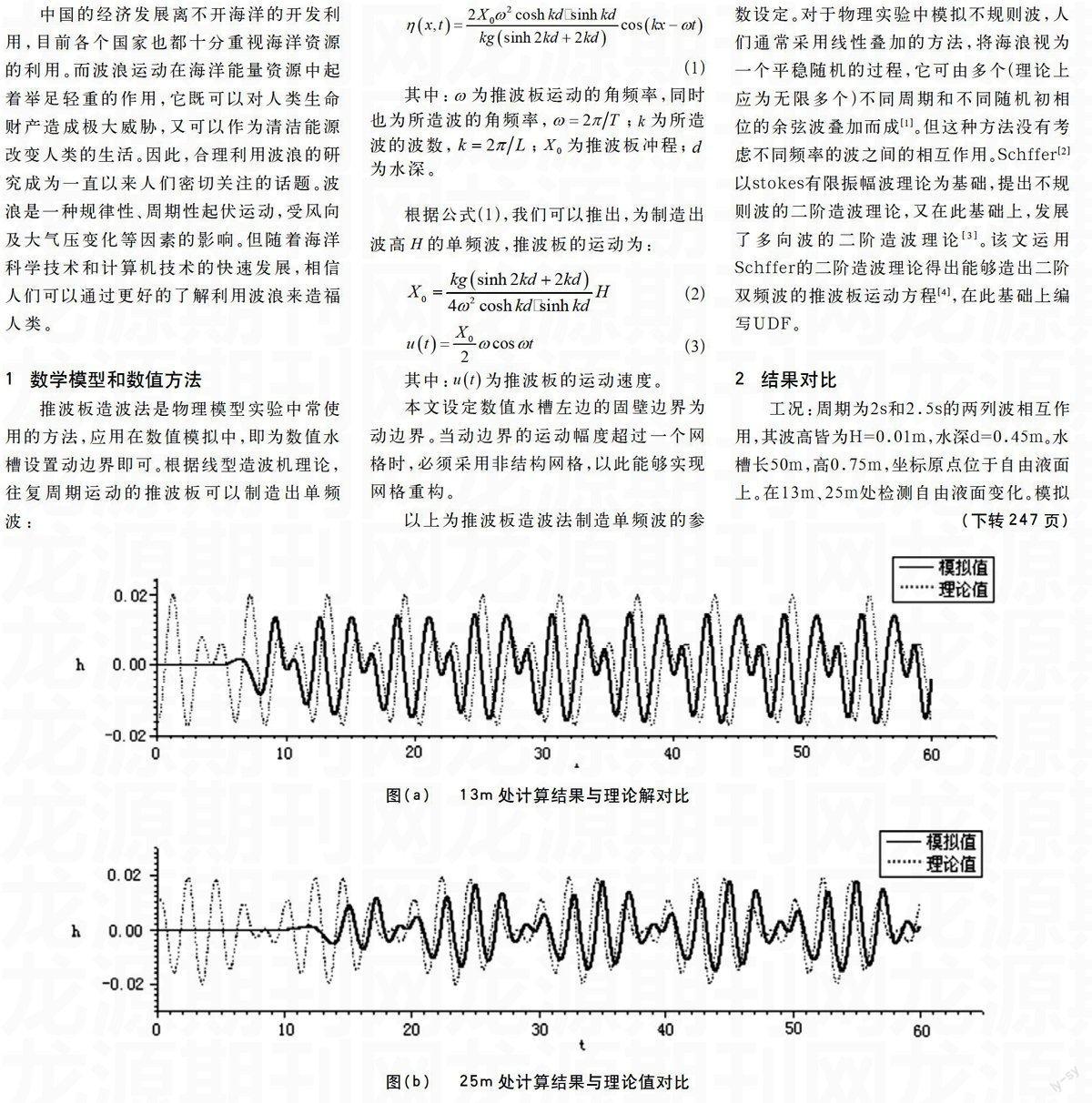
工况:周期为2s和2.5s的两列波相互作用,其波高皆为H=0.01m,水深d=0.45m。水槽长50m,高0.75m,坐标原点位于自由液面上。在13m、25m处检测自由液面变化。模拟结果如下图(a)、(b)所示:
图(a) 13m处计算结果与理论解对比
图(b) 25m处计算结果与理论值对比
3、 计算结果分析
由图可知,周期为2s和2.5s的规则波相互作用,13m处的计算结果在10s时趋于稳定,并略小于理论值。其原因为由于水的粘性作用只是波浪传播有能量耗散,而且由于波波相互作用衍生出其他频率的波,根据能量守恒定律,也会导致波高小于理论值。 25m处计算结果,随着波浪传播,波波相互作用更加显著,则有明显的衰减现象。
4、 结论
本文基于Fluent流体分析软件,运用软件自带的用户自定义函数功能,并通过stokes有限振幅波理论,推出二阶造波方程并运用到推波板造波方法中,可以成功模拟出两列波的传播。模拟值与理论值相比略小,其与实际相符,同时证明了波传播中能量的耗散,以及波波相互作用可以衍生出其他频率的波种。
参考文献:
[1] 俞聿修. 随机波浪及其工程应用[M]. 大连理工大学出版社, 1992.
[2] Hemming A. Schaffer. Second-order wavemaker theory for irregular waves[J]. Danish Hydraulic Institute, accepted 30 November 1994.
[3]H.A.Schaffer,C.M.Steenberg. Second-order wavemaker theory for multidirectional waves[J] .DHI Water & Environment,accepted 21 August 2002.
[4] 辛颖.FluentUDF方法在数值波浪水槽中的应用研究[D].大连理工大学学位论文,2013.
