一种平面稀疏阵列的快速综合方法*

陈金立,张 涛,曹华松,李家强

(南京信息工程大学电子与信息工程学院,南京210044)

一种平面稀疏阵列的快速综合方法*

陈金立**,张 涛,曹华松,李家强

(南京信息工程大学电子与信息工程学院,南京210044)

以快速综合出满足期望方向图以及阵元数最少的平面阵列为目标,提出一种基于迭代加权ℓ1范数的平面阵列综合方法。该方法将平面稀疏阵列综合问题转化为加权ℓ1范数最小化的稀疏信号重构过程,并利用拉格朗日乘数法求解每次迭代中的阵列加权向量的闭式解,由于二维平面的空间采样导致闭式解中存在大规模矩阵的求逆运算,进而引入共轭梯度法以促进算法加速收敛。当满足迭代终止条件时,由加权向量的非零值确定平面阵列的阵元位置及其激励。仿真结果表明,该方法能有效提高平面稀疏阵列综合的收敛速度。

平面稀疏阵列;阵列综合;加权ℓ1范数;闭式解;共轭梯度

1 引 言

近年来,天线阵列在雷达、通信、制导以及卫星广播电视等领域得到了广泛应用[1]。为了降低系统的软硬件复杂度和成本,在实际工程中通常要求阵列能以尽可能少的天线阵元数达到大阵列孔径以获得较高的空间分辨率[2],同时保持较低的副瓣电平。因此,采用非均匀稀疏阵列是一个有效的解决方法。然而,阵元的稀疏布置往往会导致方向图的副瓣电平抬高,天线阵列综合的目的是在保持较低的副瓣电平基础上,通过优化阵元位置及其激励的方式使得天线阵列能够以最少的阵元数满足期望的辐射特性要求[3-6]。

综合非均匀阵列的阵元位置和激励是一个包含多个未知量的高度非线性优化问题[4]。随着计算机技术的发展,遗传算法[7-8]、模拟退火算法[9]以及粒子群算法[10]等智能优化算法广泛应用于阵列综合中,但是这些传统优化算法本质都是基于随机性的自然算法,应用于求解大规模稀疏阵列时,需要很长的时间才能获得阵列综合结果。稀疏阵列的离散空间分布特点与最近发展的信号重构理论中稀疏信号的特性相类似,因此,天线阵列综合其实可以看作是空间稀疏信号重构的问题[11]。文献[4]研究了基于迭代加权ℓ1范数最小化的线性天线阵列综合方法,能以较少的迭代次数获得稀疏程度更高的线性天线阵列,但是在每次迭代中需要使用凸优化软件求解ℓ1范数最小化问题,阵列综合的耗时会比较长。文献[5]提出了一种改进的基于迭代加权ℓ1范数的线性天线阵列综合方法,在每一次迭代中给出了线性天线阵列的加权向量闭式解,避免了使用软件工具进行优化求解,实现了稀疏线性阵列的快速综合。

与线性天线阵列不同,大型的平面天线阵列能同时测量目标的空间二维角度(俯仰角和方位角),因此它在实际工程中具有无可替代的作用。文献[6]研究了基于迭代加权ℓ1范数最小化的平面阵列综合方法,然而该方法需要使用优化工具如凸优化工具来求解平面阵列的综合问题。由于优化工具的使用导致该方法的通用性和可移植性较差,而且平面阵列通常包含较多的阵元,因此采用该方法会面临巨大的计算负担。为此,本文提出了一种平面稀疏阵列的快速综合方法。该方法先利用加权ℓ1范数最小化的稀疏重构方法建立平面稀疏阵列综合的模型,然后利用拉格朗日乘数法[5]求解出每次迭代中的平面阵列加权向量的闭式解。通过分析该闭式解可知,其运算时间主要集中在矩阵求逆运算,然而求逆矩阵的规模与期望方向图的空间角度采样数有关,在平面阵列综合时其二维空间角度采样数非常大,从而导致闭式解中存在大规模的矩阵求逆运算。为了进一步加速平面阵列综合的收敛速度,该方法引入了共轭梯度方法[12-13]来解决闭式解中大规模矩阵求逆问题。仿真结果表明,该方法在给定平面阵列规模和峰值旁瓣电平等约束条件下,可快速获得最大稀疏化的平面阵列,并同时给出阵元位置及其激励幅度,特别适用于平面阵列优化的实时性和通用性要求较高的场合。

2 平面稀疏阵列模型

考虑如图1所示的X-Y平面上由M行和N列个阵列单元构成的平面稀疏阵列,图中黑点表示阵元。假设dx和dy分别表示沿X轴和Y轴方向阵元间距,信号的俯仰角和方位角分别为θ和φ。若第(m,n)个位置上天线单元的激励值为wmn,其中m= 1,2,…,M,n=1,2,…,N,则平面阵列波束方向图可以表示为[2]

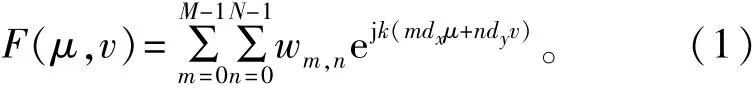
式中,k=2π/λ,其中λ为波长;方向参数μ和v分别表示为μ=sinθcosφ,v=sinθsinφ;俯仰角θ和方位角φ的定义域分别为θ∈[0,π/2],φ∈[0,2π],则方向参数μ和v的取值范围分别为μ∈[-1,1],v∈[-1,1]。本文在对平面阵列综合时,分别对μ和v在其取值范围内等间距采样,其中采样数分别记为Lμ和Lv,那么共有Lμ×Lv采样点组成了平面阵列方向图。

图1 平面稀疏阵列结构Fig.1 Configuration of planar sparse array

平面阵列的加权矩阵W2D由各阵元的激励值wmn构成[3],即

将二维加权矩阵W2D进行向量化处理,即将矩阵W2D转换成一维矢量w,即w=表示向量的转置。令a(μ,v)=其中,amn=和a(μ,v)分别代入式(1),则F(μ,v)可表示为

假设方向参数μ和v在其取值范围内的采样值分别为μ1,μ2,…,μLμ和v1,v2,…,vLv,将平面阵列方向图在所有采样点上的值构成一个大小为LμLv×1维的矢量F,则F可表示为

式中,

3 平面稀疏阵列的快速综合方法

假设在给定的平面阵列的规模、要求的峰值旁瓣电平值等约束条件下所形成期望二维波束方向图的采样向量为Fd,则平面稀疏综合问题采用加权ℓ1范数优化模型表示如下:

式中,Z是一个由加权系数zi(i=1,2,…,MN)组成的对角矩阵,可以促进矢量w尽可能地稀疏[4];Fd为期望的平面阵列波束方向图;‖·‖1表示为向量的ℓ1范数;‖·‖2为向量的ℓ2范数;ξ表示可以接受的误差。为了使综合出的阵列方向图与期望波束方向图尽可能接近,但这并不要求所有阵元都需要被激励,如果某个阵元的激励值为零或接近于零,则该位置上是无需放置阵元的,即阵列中的阵元是可以稀疏布置的。同时,稀疏阵列的离散空间分布特点与信号重构理论中稀疏信号特性类似,因此,天线阵列综合其实可以看作是空间稀疏信号重构的问题,故需要寻求一组由各阵元激励值构成的最优权值w,在保证综合后的阵列方向图接近于期望阵列方向图的条件下即‖Fd-Aw＜ξ,希望w尽可能的稀疏,即使得w中的绝大多数元素趋近于零或等于零,即满足mwin f(w)=‖Zw‖1。

利用式(7),可以将平面稀疏阵列综合问题转化为加权ℓ1范数最小化的稀疏重构问题,因此可以利用拉格朗日乘数法[5]来求解稀疏向量w的闭式解。通过构造拉格朗日函数的方法将式(7)表示的约束优化问题转换为无约束优化问题[5]:

式中,α为拉格朗日因子。将无约束优化目标函数f w,() Z展开,可得

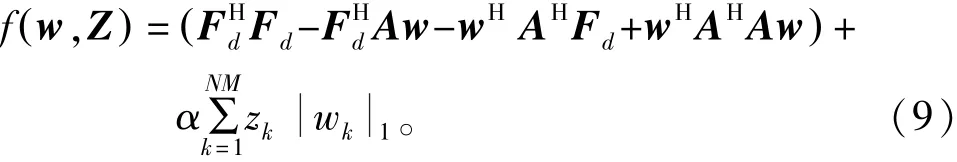
式中,[·]H表示共轭转置。为了能得到使f( w,Z)最小化时阵列加权向量w的值,在式(9)中,对wH进行求偏导数,并使得导数值等于零[5],即

求解该非线性方程(10)可获得阵列加权向量w的表达式[5]:

式中,I表示大小为MN×MN维的单位矩阵;P= diag(p),其中p=[p1,p2,…,pMN],且pi=wi/zi, i=1,2,…,MN。由于pi=wi/zi,i=1,2,…,MN,因此P是w和Z的非线性函数,那么不易直接通过式(11)来计算w的值,可采用迭代方式来求解w的值,即利用上一次迭代获得的P和Z来求解当前迭代的w值[5]。

令矩阵G=(αI+APAH),向量Y=G-1Fd,代入式(11)可得

在向量Y的表达式中,由于矩阵G的规模与空间二维角度采样数有关,而平面稀疏阵列的空间角度为二维角度(方位角和俯仰角),相比空间角度为一维角度的线性阵列,其空间角度采样数会呈平方式增长,因此平面阵列综合时矩阵G的规模会非常大,从而导致矩阵G的求逆耗时比较长,因此整个平面阵列优化过程中时间开销较大的一块是大规模矩阵G的求逆运算。根据向量Y=G-1Fd的表达形式,可以将向量Y的求解看作是线性方程组GY=Fd的求解,则可利用共轭梯度法[12-13]来加快线性方程组的求解效率,从而解决大规模矩阵求逆的问题,提高算法的实时性。共轭梯度法能有效地利用最速下降法在初始迭代点收敛快的优势,结合共轭方向找到合适的搜索方向,以最快的速度找到满足条件的收敛点,提高整个算法的运行效率。

根据以上分析,下面给出平面稀疏阵列快速综合的具体步骤。

第1步 初始化。根据给定的平面阵列横向长度和纵向长度,设置一个阵元均匀排布的初始化平面阵列,其横向阵元间距为dx,纵向阵元间距为dy,其横向阵元数为M,纵向阵元数为N,根据方向参数μ和v在其取值范围内的采样值生成矩阵A,并给定期望二维波束方向图的采样向量为Fd,令迭代次数l=0:

第2步 更新目标参数:

式中,(·)(l+1)表示第(l+1)次迭代。为了提高式(16)的计算速度,通过共轭梯度法求解线性方程组G(l+1)Y(l+1)=Fd来获得Y(l+1)值,具体步骤如下[13]:

(1)初始化。选取初始点Y0,计算r0=Fd-G(l+1)Y0,并取q0=r0,设定允许误差ε＞0,令k=0;

(2)检查是否满足终止准则。若‖rk‖1＜ε,迭代终止,输出Y(l+1)≈Yk,否则转步骤3;

(3)进行一维搜索。求出gk和Yk+1:

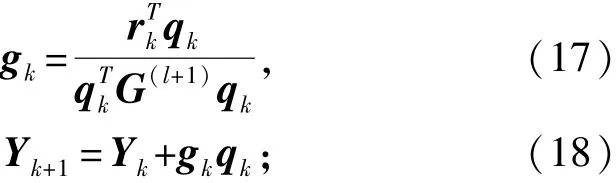
(4)计算

(5)置k=k+1,转步骤2。

第3步 计算加权:

式中,δ是一个大于零的常数,用于保证分母恒不为零。

第4步 更新矩阵P(l+1):

同时令迭代次数l=l+1。

第5步 重复第2～4步,满足下面的终止条件进入第6步:

式中,Δ为预先给定的误差最小值。

第6步 确定平面稀疏阵列的阵元位置和激励:将加权向量w转换成二维加权矩阵,其中非零元素所在的位置确定为优化后平面稀疏阵列的阵元位置,该阵元的激励值即为该非零元素值。

4 仿真实验

为了验证本文方法在平面阵列综合方面的优势,本文设计了利用迭代凸优化方法[6]和本文方法进行平面阵列综合的对比实验。以下仿真实验均在MATLAB 2012b中完成,计算机配置为:Intel Core i5-4570处理器,主频3.2 GHz,内存4 GB。

仿真参数设置如下:平面阵列横向长度为5λ,纵向长度为5λ,横向阵元间距dx=λ/4,纵向阵元间距dy=λ/4,则初始化平面阵列的横向阵元数M= 21,纵向阵元数N=21,即综合前的阵元总数为441。要求阵列综合后波束方向图旁瓣电平小于-20 dB,设置方向参数μ和v在其取值范围内的采样数分别为Lμ=41和Lv=41,误差最小值Δ=10-7。上述这些仿真参数是由平面阵列的孔径长度和期望阵列波束图等所决定,这与实际工程中阵列综合的要求一致,从而能得出可靠的结论。两种阵列综合方法都由终止条件式(24)决定其是否退出运算。

图2和图3分别是利用迭代凸优化方法和本文方法综合后的平面阵列的阵元位置分布及其波束方向图。

图2 利用凸优化方法和本文方法综合后的阵元位置分布Fig.2 The locations of sensors in the planar sparse arrays synthesized by the sequential convex optimization method and the proposed method

图3 迭代凸优化方法和本文方法综合后的平面阵列波束方向图Fig.3 Beam pattern of the planar sparse array synthesized by the sequential convex optimization method and the proposed method

由图2(a)和图3(a)可知,经过迭代凸优化方法综合后的平面阵列只需采用62个阵元就可满足给定的波束方向图旁瓣电平要求,但是该方法需要的综合时间为781 s。由于平面阵列通常包含较多的阵元以及综合时优化工具的使用,因此该方法的平面阵列综合时间较长。由图2(b)和图3(b)可知,本文方法综合后的平面阵列需要68个阵元使得波束旁瓣电平小于-20 dB,比迭代凸优化方法多用了6个阵元,但是本文方法只需要12.9 s即可快速完成平面阵列的综合,相比迭代凸优化方法,本文方法节省了约98.3%的运算时间。

文献[6]提出了基于迭代加权ℓ1范数最小化的平面阵列综合方法仅仅对波束方向图的旁瓣能量进行约束,而本文方法在整个观测角度范围内对整个波束方向图的形状进行约束,因此本文方法综合出的阵列方向图能够逼近给定的期望波束方向图,更加符合实际工程需求。从目标函数的约束条件角度分析,由于本文方法的约束条件要比凸优化方法复杂,导致其综合后的阵元数会略多于凸优化方法。为了验证平面阵列综合时引入共轭梯度方法的有效性,在本文方法第2步中不采用共轭梯度法来求解大规模矩阵求逆,即直接利用求逆公式计算每步迭代中的阵列加权向量w值,则需要阵列综合的时间为21.1 s,表明引入共轭梯度法能进一步加快平面阵列综合的收敛速度。因此,本文方法在每次迭代中利用闭式解并引入共轭梯度法来更新阵列加权向量,而无需使用优化工具来求解平面阵列的综合问题,加快了平面阵列综合的速度,特别适用于平面阵列优化的实时性和通用性要求较高的场合。

在本文仿真中,为了使得两种方法综合后的阵元位置分布能够清晰地表示出来,故只选择规模较小的初始化平面阵列进行综合分析。当初始化平面阵列的规模增大时,两种方法的阵列综合时间的差异会更明显。例如选择初始化平面阵列的横向阵元数M=50,纵向阵元数N=50,其他仿真参数同上,分别利用本文方法和凸优化方法进行阵列综合,本文方法仅需30 s完成阵列综合,而凸优化方法却需要7 h以上。此时需要采用高性能服务器来提高凸优化方法的运算速度,从而减少用户的等待时间,而本文方法仍然继续可以使用普通电脑进行优化计算。由于本文方法对硬件设备的要求不高,使得其适用范围较广以及实用性也会较好。

5 结束语

相比线性天线阵列,平面阵列通常包含较多的阵元及其波束方向图中空间二维角度采样数会呈平方式增长,从而导致现有平面稀疏阵列综合方法的耗时很长。本文提出了一种平面稀疏阵列的快速综合方法,利用闭式解来计算每次迭代过程中的阵列加权向量,当满足迭代终止条件时由加权向量中非零值确定平面阵列的阵元位置及其激励。考虑到闭式解中存在大规模矩阵求逆运算,引入共轭梯度法解决大规模矩阵的快速求逆,以促进算法加速收敛,从而提高平面阵列综合的收敛速度。此外,本文方法只通过理论仿真证实其在平面阵列综合方面的有效性,但还未在实际工程中应用,因此该方法的实用性论证将是下一步的研究内容。

[1] 吴海洲,王鹏毅,郭肃丽.全空域相控阵测控系统波束形成分析[J].无线电工程,2011,41(11):13-15. WU Haizhou,WANG Pengyi,GUO Suli.Analysis on Beamforming of Whole Airspace Phased Array TT&C System[J].Radio Engineering of China,2011,41(11):13-15.(in Chinese)

[2] 曾伟一,梁颖,黄伟.基于迭代FFT算法的平面稀疏阵列优化方法[J].电讯技术,2011,50(11):99-102. ZENG Weiyi,LIANG Ying,HUANG Wei.An Optimum Method for Thinned Planar Array Based on Iterative FFT Algorithm[J].Telecommunication Engineering,2011,50 (11):99-102.(in Chinese)

[3] 崔玉国,李清亮,闫玉波.二维矩形阵列天线方向图综合[J].现代电子技术,2009(3):65-68. CUI Yuguo,LI Qingliang,YAN Yubo.Pattern Synthesis of Two-dimensional Rectangular Antenna Arrays[J]. Modern Electronics Technique,2009(3):65-68. (in Chinese).

[4] PRISCO G,DURSO M.Maximally Sparse Arrays Via Sequential Convex Optimization[J].IEEE Antennas and Wireless Propagation Letters,2012(11):192-195.

[5] 涂光鹏,巩朋成,蔡竟业,等.基于迭代加权L1范数的稀疏阵列综合[J].计算机工程与应用,2015,51(7): 229-232. TU Guangpeng,GONG Pengcheng,CAI Jingye,et al. Sparse Array Synthesis Based on Iterative Weighted L1Norm[J].Computer Engineering and Applications,2015, 51(7):229-232.(in Chinese)

[6] FUCHS B.Synthesis of Sparse Arrays With Focused or Shaped Beampattern via Sequential Convex Optimizations [J].IEEE Transactions on Antennas and Propagation, 2012,60(7):3499-3503.

[7] 彭祥龙.用遗传算法优化任意稀布率的平面阵列[J].电讯技术,2007,47(3):153-158. PENG Xianglong.Using Genetic Algorithm to Optimize Thinned Planar Arrays with Arbitrary Thinned Factor[J]. Telecommunication Engineering,2007,47(3):153-158. (in Chinese)

[8] 夏菲,陶海红,李军.基于改进遗传算法的非均匀稀布阵列优化[J].雷达科学与技术,2009,7(6):466-471. XIA Fei,TAO Haihong,LI Jun.Optimal Design of Nonuniform Sparse Arrays Based on Modified Genetic Algorithm[J].Radar Science and Technology,2009,7(6): 466-471.(in Chinese)

[9] 廖先华,杨建红,张立军,等.基于模拟退火算法的平面稀疏阵优化[J].现代雷达,2012(10):57-59. LIAO Xianhua,YANG Jianhong,ZHANG Lijun,et al.Optimization of Planar Sparse Array Using Simulated Anneal Algorithm[J].Modern Radar,2012(10):57-59. (in Chinese)

[10] DELIGKARIS K V,ZAHARIS Z D.Thinned planar array design using boolean PSO with velocity mutation [J].IEEE Transactions on Magnetics,2009,45(3): 1490-1493.

[11] 杨鹏,闫飞,张胜辉,等.基于FOCUSS算法的稀疏阵列综合[J].电子科技大学学报,2014,43(2):203-206. YANG Peng,YAN Fei,ZHANG Shenghui,et al.Sparse Array Synthesis Based on FOCUSS Algorithm[J].Journal of University of Electronic Science and Technology of China,2014,43(2):203-206.(in Chinese)

[12] 杨俊杰,刘海林.增广Lagrange函数优化算法在稀疏信号重构问题中的应用[J].计算机科学,2011,38 (9):193-196. YANG Junjie,LIU Hailin.Application of Augmented Lagrange Optimization Algorithm to the Sparse Signal Reconstruction Problem[J].Computer Science,2011,38 (9):193-196.(in Chinese)

[13] 郑丽.几种共轭梯度法的研究[D].重庆:重庆大学,2009. ZHENG Li.Study on Several Conjugate Gradient Methods [D].Chongqing:Chongqing University,2009.(in Chinese)

CHEN Jinli was born in Ningbo,Zhejiang Province,in 1982.He received the Ph.D.degree in 2010.He is now a lecturer.His research concerns MIMO radar signal processing.

Email:chen820803@yeah.net

张 涛(1986—),男,新疆伊宁人,硕士研究生,主要研究方向为气象相控阵雷达;

ZHANG Tao was born in Yining,Xinjiang Uygur Autonomous Region,in 1986.He is now a graduate student.His research concerns weather phased array radar.

曹华松(1989—),男,江苏泰州人,硕士研究生,主要研究方向为天线阵列综合;

CAO Huasong was born in Taizhou,Jiangsu Province,in 1989.He is now a graduate student.His research concerns antenna array synthesis.

李家强(1976—),男,安徽滁州人,2007年获博士学位,现为副教授,主要研究方向为雷达信号处理。

LI Jiaqiang was born in Chuzhou,Anhui Province,in 1976. He received the Ph.D.degree in 2007.He is now an associate professor.His research concerns radar signal processing.

A Fast Synthesis Method for Planar Sparse Array

CHEN Jinli,ZHANG Tao,CAO Huasong,LI Jiaqiang
(College of Electronic and Information Engineering,Nanjing University of Information Science and Technology,Nanjing 210044,China)

In order to fast synthesize the planar array to satisfy the desired pattern and minimize the number of radiating elements,a planar array synthesis method based on iteratively reweighted ℓ1norm minimization is proposed.The problem of planar array synthesis is transformed into a process of the sparse signal reconstruction based on reweighted ℓ1norm minimization,and the closed-form solution of the array weight vector at each iteration is obtained by the Lagrange multiplier method.Due to the inverse operation of the largescale matrix caused by the two dimensional spatial sampling in the closed-form solution,the conjugate Gradient method is introduced to promote the convergence speed of the proposed method.The excitations and locations of sensors in the planar sparse array are determined by the nonzero elements in the solved weight vector until the iteration termination condition is satisfied.Simulation results show that the proposed method can effectively speed up the planar sparse array synthesis.

plannar sparse array;array synthesis;weighted ℓ1norm;closed-form solution;conjugate gradient

The National Natural Science Foundation of China(No.61302188,61372066);The Natural Science Foundation of Jiangsu Province(BK20131005)

date:2015-04-24;Revised date:2015-07-06

国家自然科学基金资助项目(61302188,61372066);江苏省自然科学基金资助项目(BK20131005)

**通讯作者:chen820803@yeah.net Corresponding author:chen820803@yeah.net

TN957.2

A

1001-893X(2015)12-1318-06

陈金立(1982—),男,浙江宁波人,2010年获博士学位,现为讲师,主要研究方向为MIMO雷达信号处理;

10.3969/j.issn.1001-893x.2015.12.002

陈金立,张涛,曹华松,等.一种平面稀疏阵列的快速综合方法[J].电讯技术,2015,55(12):1318-1323.[CHEN Jinli,ZHANG Tao,CAO Huasong,LI Jiaqiang.A Fast Synthesis Method for Planar Sparse Array[J].Telecommunication Engineering,2015,55(12):1318-1323.]

2015-04-24;

2015-07-06