基于最小二乘法的海基双站测量数据综合处理*

陈红英,郭才发,向 颉,倪 兴

(中国卫星海上测控中心,江苏江阴214431)

基于最小二乘法的海基双站测量数据综合处理*

陈红英**,郭才发,向 颉,倪 兴

(中国卫星海上测控中心,江苏江阴214431)

针对测量船执行海上任务单船数据处理及弹道参数计算受时间和弧段限制局限性的问题,提出了采用加权最小二乘法解算双站目标坐标的综合数据处理方法,并在综合后的数据库增加了跟踪时间及重要特征点弧段数据,提高了位置及其他弹道参数的估计精度。该方法的推广对改进测量船数据处理方法和技术、提高弹道状态估计精度均具有积极的意义。

航天测量船;弹道计算;海基双站测量数据;综合处理;最小二乘法

1 引 言

测量船外弹道测量数据精度对航天测控有着重要的意义,外弹道测量以及数据处理是导弹和航天器飞行试验工程的重要组成部分,它对于保障导弹、航天器试验的完成和促进其技术发展具有重要的作用[1]。由于处理方法的局限性,在历史任务外测事后数据处理中,仅采用单条测量船的数据进行事后数据处理以及弹道参数的计算,由于单船(单站)的测量数据受时间和弧段的限制,使用的观测数据较少,某些重要特征点的数据无法采集,这就影响了所解算参数的精度,当两艘测量船(双站)的雷达同时跟踪飞行目标时,用于定位的测量元素增加了3个测量量。在跟踪几何较好的条件下,采用加权最小二乘法求解目标坐标可以提高定位数据及其他弹道参数的精度。

综合数据处理就是将各外测系统的观测数据汇集起来,并且利用先进的数学方法进一步修正各种误差,再根据测控方案计算出用户所需的弹道参数。为保证数据获取的高可行性和最终弹道的高精度,导弹试验时经常由多套系统联合进行弹道测量。因此,在对各外测系统的观测数据进行量纲复原及各种误差修正之后,还必须将它们汇集一起,用先进的数据处理技术和方法进行综合处理,进一步提高最终弹道的精度。另外,在预处理中,虽然对观测数据进行了各种系统误差修正,但对于误差特性的认识有限或修正模型不准确等因素,仍然存在着系统误差残差。在综合数据处理时,应充分利用观测数据的冗余度、更合理的模型和估计方法,修正这些残差[2]。

2 测量数据综合处理

综合数据处理观测量的选取与处理方案是紧密相关的,按观测量的选取不同,可将综合处理模式简单地分为两类,一是取两船测得的原始数据作为综合处理的观测量同时进行处理,二是取各船分别处理的最终结果或中间结果(即转到惯导地平系或测量系的数据)作为观测量参与综合处理。本文采用的处理方法为将两船转到惯导地平系的数据作为观测量参与综合处理[3]。

2.1 基本原理

将两船的脉冲雷达原始测量数据距离R、方位A和俯仰E经角坐标转换到惯导地平系后,再转换成测站发射坐标系的观测量,有

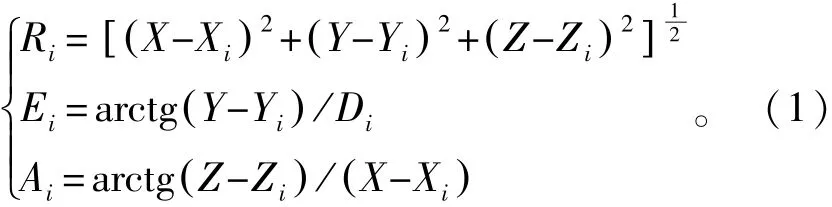
式中,i=1,2,…,n,Di=[(X-Xi)2+(Z-Zi)2]12,XYZ为目标在发射坐标系的坐标,XiYiZi为测站在发射坐标系的坐标。

现对式(1)泰勒展开成线性观测方程,则矩阵形式为

式中,L是观测向量与初始观测向量之差,A为观测向量关于弹道位置参数的雅可比矩阵,Δ¯X= (ΔX、ΔY、ΔZ)T,e是观测数据的误差向量。

根据加权最小二乘原理,得到

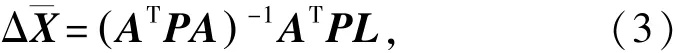
于是得到目标的最小二乘估计为

式中,¯X0是由其他方法得到的初始弹道位置参数,P为观测误差向量的协方差矩阵之逆。

2.2 弹道参数综合处理

2.2.1 目标位置的计算

若在发射系中视两船分别求解的目标位置为测量元素,则可得到形式极其简单的观测方程组。令¯X1=(X1、Y1、Z1)T和¯X2=(X2、Y2、Z2)T分别为两船单独处理得到的位置坐标数据,¯X=X、Y、() ZT为待求的目标位置参数,e1、e2分别为误差向量,则得到观测方程组为

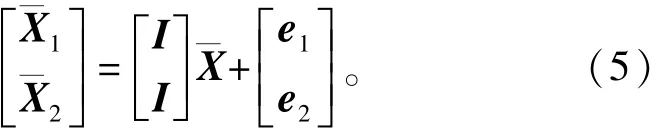
式中,I为单位阵,取权矩阵为P=diag P1,P()2。则利用式(3)得到目标位置的综合处理结果为

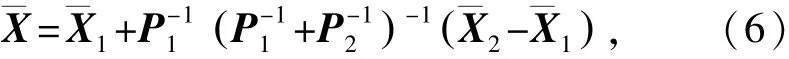
和协方差矩阵为

2.2.2 速度参数的计算

如果脉冲雷达能得到精度较高的斜距变化率R˙,则在位置分量x、y、z微分平滑获取分速度x˙、y˙、z˙的基础上,对R˙观测量应用递推最小二乘估计,可得到精确的分速度。在此,以具有两个R˙为例,并假设第1、2台的观测量为R˙i( i=1,2),则有

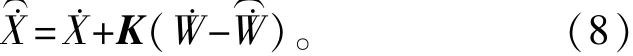
式中,X˙=(x,y,z)T为新的分速度参数估计值,X˙= (x,y,z)T为微分平滑后分速度参数,W˙=(R˙1,R˙2)T为观测向量,而W˙ =(R˙1,R˙2)T,由x、y、z和x、y、z代入下式得到,即

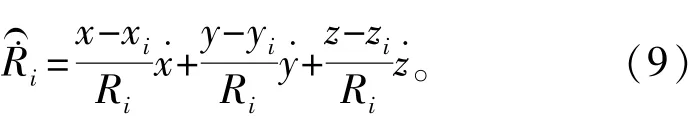
式中,i=1,2,xi、yi、zi为第i台脉冲雷达的站址坐标;Ri=[(x-xi)2+(y-yi)2+(z-zi)2]12。而增益矩阵K为K=PX˙HT(PR˙+HPX˙HT)-1,式中,PX˙为微分平滑后的估计值X˙=(x˙,y˙,z˙)T的误差协方差阵,

式中,σ˙Ri为˙Ri的随机误差均方差。

2.2.3 加速度及其他参数的计算

利用三阶多项式中心平滑,直接由脉冲雷达观测数据解算的弹道位置参数xi、yi、zi得到加速度参数,由分速度和分加速度计算其他弹道参数(合成速度V、倾角θ和偏角σ等)[4]。

3 工程应用效果及分析

以历史任务X的数据处理为例,在X卫星发射测控任务中,测量船A、测量船B共同完成海上测控任务。测量船A承担任务包括T1、T2、T3特征点数据,测量船B承担任务包括T3、T4、T5特征点数据,跟踪情况如图1所示。

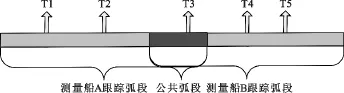
图1 双站跟踪示意图Fig.1 The sketch map of bi-station tracking

如果未对双站数据进行综合处理,采用传统的单船事后数据处理计算弹道参数,提交弹道参数报告的数据为测量船B跟踪弧段数据,仅包含T3、T4、T5特征点。

测量船双站录取的外测数据正常有效,在确保精度测量范围内,分别对两船数据进行数据预处理,转至惯导地平系,并采用加权最小二乘法进行数据综合处理,最后对综合处理后的数据进行弹道参数的解算。经过综合处理后的弹道参数由三部分组成,即测量船A弹道数据、测量船AB综合弹道数据、测量船B弹道数据,具体描述见图2～4。

图2 双站弹道综合数据示意图(X方向距离)Fig.2 The synthetic data of the trajectory for the bi-station (distance in X direction)

图3 双站弹道综合数据示意图(X方向速度)Fig.3 The synthetic data of the trajectory for the bi-station (velocity in X direction)

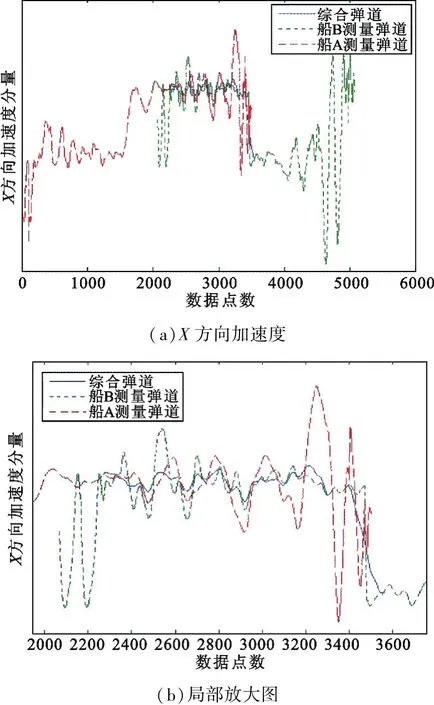
图4 双站弹道综合数据示意图(X方向加速度)Fig.4 The synthetic data of the trajectory for the bi-station (acceleration in X direction)

在图2～4中绘制了双站目标在X方向的距离、速度、加速度的运动轨迹,从图中可以清楚地看到各测量船的弹道参数以及综合处理后的弹道曲线。综合处理后的数据包括了T1～T5重要特征点的数据,记录了目标的飞行轨迹,弥补了单船处理时缺少重要弧段和特征点数据的不足,大大提高了定位数据及其他弹道参数的精度。

4 结束语

采用最小二乘法求解测量船双站目标坐标的综合数据处理方法对于不断改进测量数据处理方法和技术、提高弹道测量数据精度有重要的意义[5]。经过试算和验证,综合处理方法有效地计算了双站数据弹道,提高了数据的利用率,为用户评定、分析导弹和运载火箭的性能和精度,为改进型号设计和定性提供了依据。综合处理后的数据真实反映了目标的飞行轨迹以及在特征点的参数特性,提高了外弹道测量数据精度。

[1] 江文达.航天测量船[M].北京:国防工业出版社, 2002:13-129. JIANG Wenda.Space Tracking Ships[M].Beijing:National Defense Industry Press,2002:13-129.(in Chinese)

[2] 刘利生.外弹道测量数据处理[M].北京:国防工业出版社,2002:225-318. LIU Lisheng.Data Processing of Exterior Trajectory[M]. Beijing:National Defense Industry Press,2002:225-318. (in Chinese)

[3] 傅敏辉,康德勇,王旭良,等.测量船外测数据的四矢量误差分析方法[J].电讯技术,2013,53(10):1269-1273. FU Minhui,KANG Deyong,WANG Xuliang,et al.Four-Vector-Error Analysis Method for Exterior Measurement Data Based on TT&C Ship[J].Telecommunication Engineering,2013,53(10):1269-1273.(in Chinese)

[4] 陈红英.基于弹道计算的截断误差估计与补偿[J].无线电工程,2011,41(8):9-11. CHEN Hongying.Estimate and compensate to Truncation error base on Trajectory calculate[J].Radio Engineering of China,2011,41(8):9-11.(in Chinese)

[5] 陈红英,李辉芬.航天测量船角度系统误差偏大问题的分析与解决[J].电讯技术,2011,51(10):71-75. CHEN Hongying,LI Huifen.Analysis of and Solution to Relatively Large Azimuth System Error Problem in a Task by Space TT&C Ship[J].Telecommunication Engineering,2011,51(10):71-75.(in Chinese)

CHEN Hongying was born in Yingshan,Sichuan Province,in 1982.She received the B.S. degree in 2005.She is now an engineer.Her research concerns maritime measurement data processing and precision analysis.

Email:9132536@qq.com

郭才发(1986—),男,江西南康人,2014年获博士学位,现为工程师,长期从事海上测量数据处理工作;

GUO Caifa was born in Nankang,Jiangxi Province,in 1986. He received the Ph.D.degree in 2014.He is now an engineer. His research concerns space tracking data processing.

向 颉(1982—),男,湖南龙山人,2014年获硕士学位,现为工程师,长期从事海上测量数据处理工作;

XIANG Jie was born in Longshang,Hunan Province,in 1982.He received the M.S.degree in 2014.He is now an engineer.His research concerns space tracking data processing.

倪 兴(1976—),男,江苏金坛人,2009年获硕士学位,现为工程师,长期从事海上测量数据处理工作。

NI Xing was born in Jintan,Jiangsu Province,in 1976.He received the M.S.degree in 2009.He is now an engineer.His research concerns space tracking data processing.

Data Processing Based on Least Squares for Sea-based Bi-station Measurement

CHEN Hongying,GUO Caifa,XIANG Jie,NI Xing
(China Satellite Maritime Tracking and Control Department,Jiangyin 214431,China)

For the shortcoming of the time and arc constraints of single ship in TT&C tasks,the weighted least squares method is applied to calculate the target states based on bi-station.Through adding the tracking time and the arc data of the feature points in the synthetic database the precision of the positioning and the other states estimation is greatly improved.The application of the method is helpful to improve the data processing technology and trajectory states estimation precision.

space TT&C ship;trajectory calculation;sea-based bi-station measurement data;synthetical processing;least squares method

date:2015-03-27;Revised date:2015-06-10

**通讯作者:9132536@qq.com Corresponding author:9132536@qq.com

TN911;TP274

A

1001-893X(2015)12-1413-04

陈红英(1982—),女,四川营山人,2005年获学士学位,现为工程师,主要从事海上测量数据处理与精度分析工作;

10.3969/j.issn.1001-893x.2015.12.018

陈红英,郭才发,向颉,等.基于最小二乘法的海基双站测量数据综合处理[J].电讯技术,2015,55(12):1413-1416.[CHEN Hongying,GUO Caifa,XIANG Jie,et al.Data Processing Based on Least Squares Method for Sea-based Bi-station Measurement[J].Telecommunication Engineering,2015,55(12):1413-1416.]

2015-03-27;

2015-06-10