新三维非线性混沌系统的动力学分析
2015-06-28付木亮张光云卢振坤
付木亮,张 勇,张光云,卢振坤
(1.河南工业职业技术学院基础教学部,河南南阳473000;2.西南石油大学外国语学院,四川成都610500;
3.广西民族大学信息科学与工程学院,广西南宁530006)
新三维非线性混沌系统的动力学分析
付木亮1,张 勇1,张光云2,卢振坤3
(1.河南工业职业技术学院基础教学部,河南南阳473000;2.西南石油大学外国语学院,四川成都610500;
3.广西民族大学信息科学与工程学院,广西南宁530006)
基于动力系统的理论和方法,采用理论分析和Matlab仿真相结合的方式,在已有文献研究的基础上,研究了一个新三维混沌系统的复杂动力学行为,包括混沌系统的散度和吸引子的存在性、平衡点及其数目、全局吸引域、对称性和正向不变集等.该研究结果是已有文献的推广,Matlab模拟验证了计算理论的正确性.
混沌系统;混沌吸引子;不变集;数值仿真
混沌的理论起源于1900年庞加莱对于三体问题的研究,发现它的运动轨迹是非周期的,也不趋于固定点.1963年,Lorenz发现了第一个混沌吸引子,从此,混沌在数学、物理、化学、计算机工程、神经网络、图像处理等领域得到了广泛的研究和应用[1-5];1999年,Chen等人发现了1个新的Chen混沌吸引子,Chen混沌吸引子与Lorenz混沌吸引子在拓扑结构上是不等价的;2002年,Chen与Lü等人发现了Lü混沌吸引子,Lü混沌吸引子是连接Lorenz混沌吸引子与Chen混沌吸引子之间的纽带;此后,Qi等人发现了一个有5平衡点的新混沌系统.从此,新的混沌系统不断得到发现,并且这些新混沌系统的动力学行为也得到了一系列的分析和应用[6].
混沌系统的吸引集是研究混沌系统定性理论的一个重要方面[4].早在1987年,Leonov首次研究了Lorenz混沌吸引子的有界性基于动力系统的理论和方法[7];2007年,Qin和Chen等人研究了Chen混沌吸引子的有界性;2010年,文献[8]研究了Lü混沌吸引子的有界性.基于以上研究工作的启发和方法,本文研究了一个新三维混沌系统的复杂动力学行为,并且给出计算机仿真.
1 数学模型及其主要结果
文献[9]提出的一个新三维混沌系统的方程为:

这里a,b,c,d为系统(1)正参数.当a=5,b=16,c=1时,系统(1)轨线相图见图1.
对于一个新的混沌系统,它的一些基本的非线性动力学行为是令人关注的.
1.1 对称性和不变性
系统(1)具有自然的对称性,即在坐标变换(x,y,z)→(-x,-y,z)下,系统(1)保持不变.z轴为系统(1)的不变集,并且从z轴上任何点出发的轨线当t→+∞时都趋于原点.
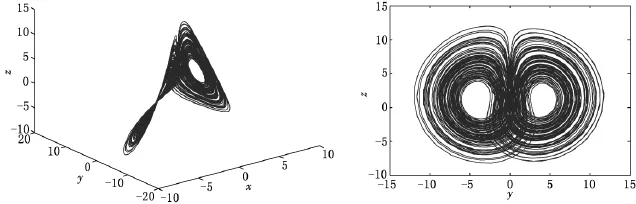
图1 系统(1)轨线的相图
1.2 耗散性和吸引子的存在性对系统(1),有:
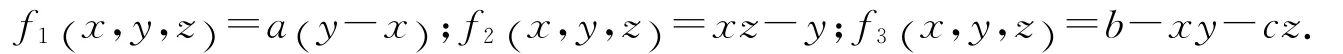
则系统(1)的散度为

1.3 平衡点
对于混沌系统(1),当b>c时,系统(1)只有3个平衡点,分别为:
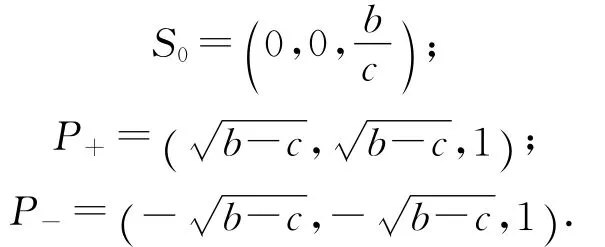
1.4 全局吸引性
定理1 对任意的a>0,b>0,c>0,λ>0,系统的轨线(1)存在指数估计式
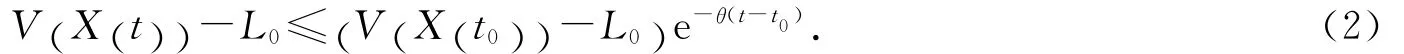
有
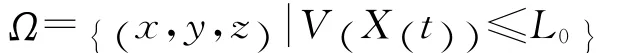
为系统(1)的一个全局指数吸引集.其中:
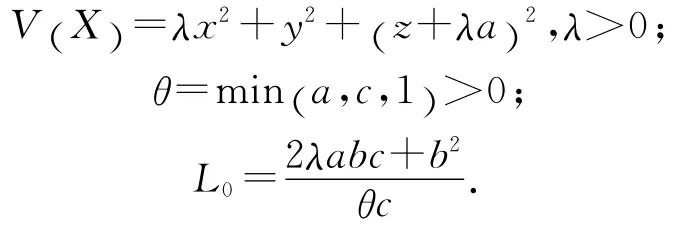
证明 定义广义正定、径向无界的李雅普函数为
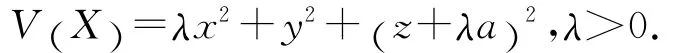
当V (X (t))>L0,V (X (t0))>L0,沿着系统(1)求导

对上述不等式两边积分,当V (X (t))>L0,V (X (t0))>L0,有

令t→+∞,对上述不等式两边取上极限
集合

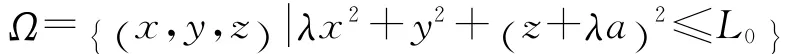
为系统(1)的一个全局指数吸引集,有
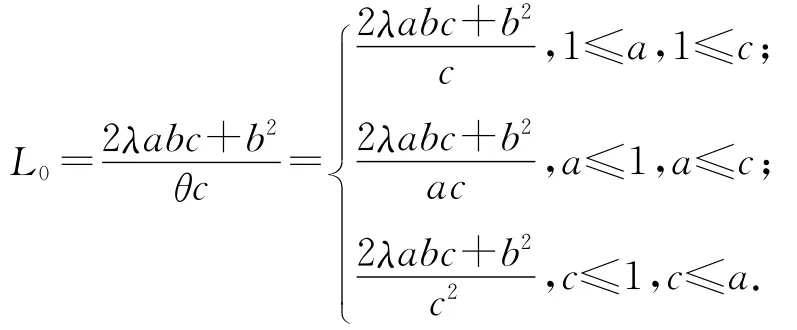
注 当λ=1时,即为文献[10]中的结果.
定理2 对任意的a>0,b>0,c>0,系统(1)存在指数估计式
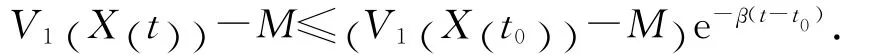
集合
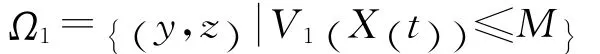
为系统(1)的一个全局指数吸引集.其中:
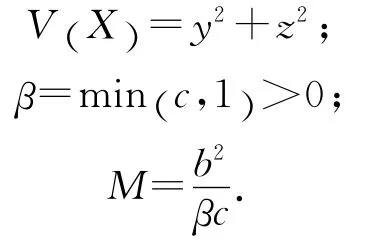
证明 定义V1(X)=y2+z2,当V1(X (t))>M,V1(X (t0))>M,沿着系统(1)求导得
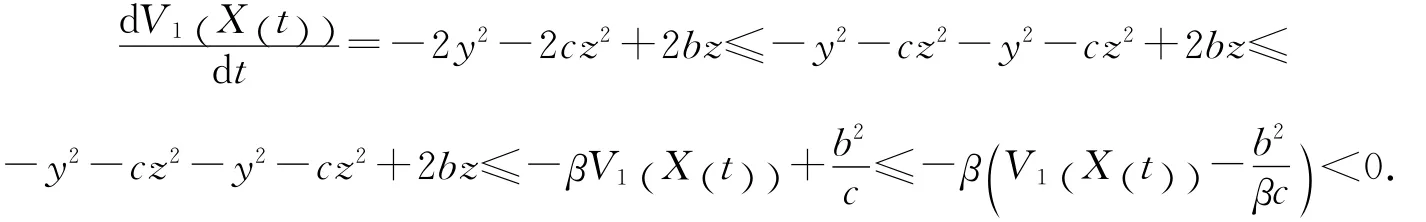
对上述不等式两边积分,当V1(X(t))>M,V1(X (t0))>M,有
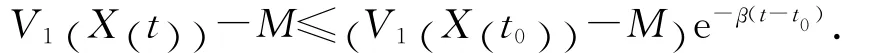
令t→+∞,对上述不等式两边取上极限
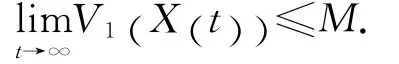
2 数值模拟
取参数a=5,b=16,c=1,这时由定理θ=min (a,c,1)=1,β=min (c,1)=1,系统的2个全局指数吸引集为:
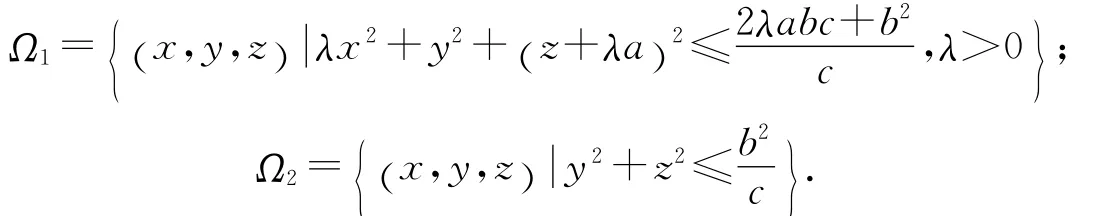
特别的,取λ=1,这时有
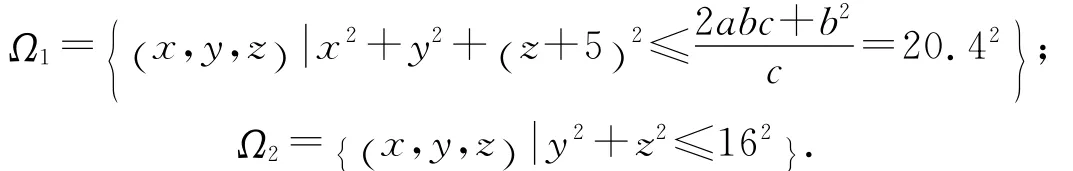
系统(1)的正半轨线界估计如图2所示.
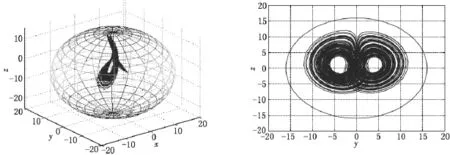
图2 系统(1)正半轨线最终界估计图
3 结论
本文基于动力系统的基本理论和方法,采用理论分析和Matlab仿真相结合的方式,在已有文献研究的基础上,研究了一个新三维混沌系统的一些复杂的动力学行为,包括新混沌系统的耗散性和吸引子的存在性、系统的对称性、混沌系统的平衡点及其个数、混沌系统的全局吸引域、系统的不变集等,对于该混沌系统吸引域的研究推广了文献中的已有结果,同时给出了相应的Matlab仿真,Matlab仿真验证了本文计算理论的可行性和正确性.
[1] 汪威,朱晓刚,李俊杰,等.Feigenbaum吸引子的动力性质[J].东北师大学报:自然科学版,2014,46(4):48-51.
[2] 梁春辉,张运波,孟祥萍,等.自适应反演控制在一类非线性系统中的应用[J].东北师大学报:自然科学版,2014,46(4):66-71.
[3] HE XING,YU JUNZHI,HUANG TINGWEN,et al.Neural networks for solving nash equilibrium problem in application of multiuser power control[J].Neural Networks,2014,57(9):73-78.
[4] ZHANG FUCHEN,ZHANG GUANGYUN,LIN DA,et al.New estimate the bounds for the generalized Lorenz system[J].Mathematical Methods in the Applied Sciences,2015,38:1696-1704.
[5] 马超,刘泉,章明朝,等.Markov分割混沌系统图像加密算法的FPGA实现[J].计算机工程与设计,2015,36(4):846-850.
[6] 张勇,付木亮.高维混沌模型的动力学分析及仿真[J].江西科学,2015,33(2):160-161.
[7] LEONOV G A,BUNIN A,KOKSCH N.Attractor localization of the Lorenz system[J].Zeitschrift für Angewandte Mathematik und Mechanik,1987,67:649-656.
[8] ZHANG FUCHEN,MU CHUNLAI,LI XIAOWU.On the boundness of some solutions of the Lüsystem[J].International Journal of Bifurcation and Chaos,2012,22(1):1-5.
[9] LI XIANFENG,CHLOUVERAKIS KONSTANTINOS E,XU DONGLIANG.Nonlinear dynamics and circuit realization of a new chaotic flow a variant of Lorenz,Chen and Lü[J].Nonlinear Analysis Real World Applications,2009,10:2357-2368.
[10] WANG GUIHE,JIAN JIGUI.Globaly exponentially attractive set and synchronization controlling of a new chaotic system[C]//Qingdao:Proceedings of the Ninth International Conference on Machine Learning and Cybernetics,2010,7:11-14.
Dynamical analysis of a new nonlinear 3Dchaotic system
FU Mu-liang1,ZHANG Yong1,ZHANG Guang-yun2,LU Zhen-kun3
(1.Department of Basic Teaching,Henan Polytechnic Institute,Nanyang 473000,China;2.School of Foreign Languages,Southwest Petroleum University,Chengdu 610500,China;3.Institute of Information Science and Engineering,Guangxi University for Nationalities,Nanning 530006,China)
Based on the theory and the method of dynamical systems,this paper further investigates complex dynamical behaviors of a new chaotic system including the chaotic attractor of the system,the divergence of the system,the equilibria of the system,the number of equilibrium point of the system,global attractive set,symmetry and invarian sets by theoretical analysis and Matlab simulation combined method.The results of this paper generalize the existing results available in the literature.Matlab simulation verifies the correctness of the theoretical calculation.
chaotic system;chaotic attractor;invariant set;matlab simulations
O 29;O 242.1 [学科代码] 110·61
A
(责任编辑:石绍庆)
1000-1832(2015)03-0068-04
10.16163/j.cnki.22-1123/n.2015.03.015
2014-02-08
广西省自然科学基金资助项目(2014GXNSFBB118005).
付木亮(1978—),男,讲师,主要从事数学理论研究.
