半群PORn理想的极大正则子半群
2015-06-28游泰杰
赵 颐,游泰杰,赵 平
(贵州师范大学数学与计算机科学学院,贵州贵阳550001)
半群PORn理想的极大正则子半群
赵 颐,游泰杰,赵 平
(贵州师范大学数学与计算机科学学院,贵州贵阳550001)
设POPn和PORn分别是Xn上的方向保序部分变换半群和方向保序或反方向保序部分变换半群.对任意2≤r≤n-1,研究了半群I(n,r)={α∈PORn:|im(α)|≤r}的极大正则子半群的结构.利用Miller-Clifford定理,证明了半群I(n,r)的极大正则子半群有且仅有两类:(ⅰ)Mα=I(n,r-1)∪(Jr\Rα),α∈Jr;(ⅱ)Nr=I(n,r-1)∪.其中:Jr={α∈PORn:|im(α)|=r},={α∈PORn:|im(α)|=r},Rα表示α所在R-类.
变换半群;方向保序;反方向保序;极大正则子半群
1 预备知识
设Xn={1,2,…,n},并赋予自然序.Pn和Tn分别为Xn上的部分变换半群和全变换半群.设c=(c1,c2,…,ct)是一个序列,其中c1,c2,…,ct∈Xn,t≥1(当t=0时,c表示空序列),若至多存在一个i∈{1,2,…,t},使得ci>ci+1(ci<ci+1)(当i=t时,ct+1=c1),则称c是一个圈(反圈).设α∈Pn且dom(α)={a1<a2<…<at},其中t≥1,若(a1α,…,atα)是一个圈(反圈),则称α是方向保序的(反方向保序的).设POPn和PORn分别为Pn中的所有方向保序部分变换之集和所有方向保序或反方向保序部分变换之集,则POPn和PORn都是Pn的子半群;称POPn和PORn分别为方向保序部分变换半群和方向保序或反方向保序部分变换半群.令OPn=POPn∩Tn,且ORn=PORn∩Tn,则OPn和ORn都是Tn的子半群;称OPn和ORn分别为方向保序全变换半群和方向保序或反方向保序全变换半群.
变换半群具有某种性质的极大子半群的研究一直以来都是半群理论研究中的热点之一[1-9].特别地,2002年,游泰杰得到了全变换半群Tn和部分变换半群Pn理想的极大正则子半群的完全分类[2],2011年,赵平与游泰杰研究了方向保序全变换半群OPn理想的极大正则子半群的结构和分类[4];I.Dimitrova与J.Koppitz得到了保序变换半群On和保序或保反序变换半群ODn理想的极大正则子半群的完全分类[5].在上述工作的基础上,本文将考虑方向保序或反方向保序部分变换半群PORn理想的极大正则子半群的结构和分类.
据文献[10]知,PORn中的Green关系刻画为:对任意α,β∈PORn,αLβ当且仅当im(α)=im(β);αRβ当且仅当ker(α)=ker(β);αJβ当且仅当|im(α)|=|im(β)|,D=J.设J0为空变换所构成的集合.对1≤r≤n,记Jr={α∈PORn:|im(α)|=r},则PORn有n+1个J-类J0,J1,…,Jn.令
引理1.1[11]设x,y是完全0-单半群中两个非零元,则xy≠0当且仅当Lx∩Ry中含有幂等元.此时,xy∈Ly∩Rx.当Lx∩Ry中含有幂等元时,xRy=Rx,Lxy=Ly,LxRy=S\{0};否则,xRy=Lxy=LxRy={0}.
设U是半群S的任意子集,通常用E(U)表示U中的幂等元之集.对任意a∈S,通常用Ra,La,Ha,Ja分别表示a所在R-类,L-类,H-类,J-类.本文未定义的术语及记法参见文献[12].
2 半群PORn理想的极大正则子半群
设PRn为Pn中的所有反方向保序部分变换之集,则显然PORn=POPn∪PRn.对0≤r≤n,设
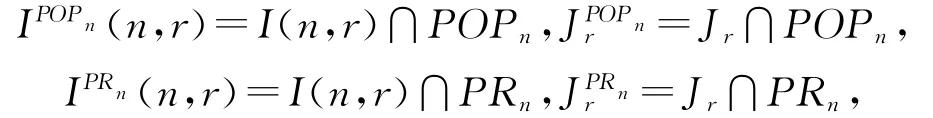
则
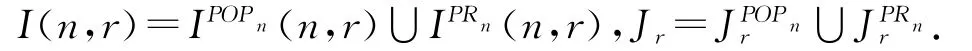
定义2.1 设2≤r≤n-1,S是I(n,r)的正则子半群(S⊂I(n,r)).若S满足:对I(n,r)的任意正则子半群T,有
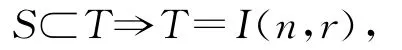
则称S是I(n,r)的极大正则子半群.
定理2.1 设2≤r≤n-1,则I(n,r)的极大正则子半群有且仅有如下两类:
(A)Mα=I(n,r-1)∪(Jr\Rα),α∈Jr;
(B)Nr=I(n,r-1)∪JPOPnr.
为证明定理2.1,我们需要以下引理:
引理2.1 设I是正则半群S的理想,则I是正则的.
证明 设x∈I,则由S的正则性可得,存在y∈S,使得x=xyx,y=yxy.于是由x∈I及I是理想可得,y=yxy∈I,从而y是x在I中的逆元.因此I是正则的.
引理2.2 POPn和PORn都是正则半群.
证明见文献[10]第746页和文献[13]的命题2.3.
引理2.3 设2≤r≤n-1,则I(n,r)和IPOPn(n,r)都是正则半群.
注意到I(n,r)和IPOPn(n,r)分别是PORn和POPn的理想.由引理2.1—2.2可推出结论.
引理2.4 设S是正则半群且E(S)是S的幂等元之集,则对任意a∈S,有
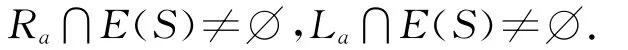
证明见文献[12]的命题2.3.1—2.3.2.
引理2.5 设S是正则半群,a,b∈S,则H-类Hb包含a的逆元的充分必要条件是
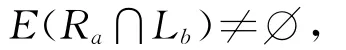
且
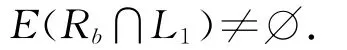
证明见文献[11]的定理2.18.
引理2.6 设2≤r≤n-1,α∈Jr,则|E(Lα)|≥2,且|E(Rα)|≥1.
证明 设
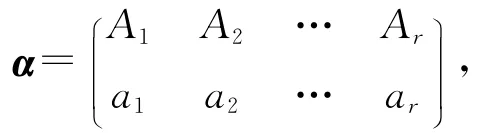
其中a1<a2<…<ar.令B1={1,…,a1};Bi={ai-1+1,…,ai},i=2,…,r-1;Br={ar-1+1,…,n};且ci=maxAi,i∈{1,2,…,r}.设

则ε,η,ρ∈E(Jr).由im(ε)=im(η)=im(α),且ker(ρ)=ker(α),可得εLηLαRρ.因此,|E(Lα)|≥2,且|E(Rα)|≥1.
引理2.7 设2≤r≤n-1,α∈Jr,则存在α的逆元α1,α2,使得(α1,α2)∉R,且α1,α2∈Jr.
证明 由引理2.6可知,|E(Rα)|≥1,且|E(Lα)|≥2.设ε1,ε2∈E(Lα),ε1≠ε2,η∈E(Rα),则(ε1,ε2)∉R(否则,ε1,ε2∈Hα,与每个H-类至多包含一个幂等元矛盾,见文献[12]的推论2.2.6).注意到εiLαRη,i=1,2.由引理2.5可得,Rε1∩Lη和Rε2∩Lη都包含α的逆元.不妨分别设为α1,α2,则εiRαi(i=1,2),从而(α1,α2)∉R.由αiRεiLα可知,αiJα,从而|im(αi)|=|im(α)|=r.因此αi∈Jr.
引理2.8 设2≤r≤n-1,α∈Jr,则Mα=I(n,r-1)∪(Jr\Rα)是I(n,r)的极大正则子半群.
证明 首先,证明Mα是I(n,r)的子半群.由引理1.1知,对任意β,γ∈Jr\Rα,有βγRβ或βγ∈I(n,r-1).因此,Mα是I(n,r)的子半群.
其次,证明Mα是I(n,r)的正则子半群.任意取β∈Mα.(ⅰ)若β∈I(n,r-1),由引理2.3知,I(n,r-1)是正则的,于是I(n,r-1)中存在β的逆元,从而β在Mα中存在逆元;(ⅱ)β∈Jr\Rα,则由引理2.7知,存在β的逆元β1,β2,使得(β1,β2)∉R且β1,β2∈Jr,从而β1,β2中至少有一个属于Mα.因此β是正则的.Mα是I(n,r)的正则子半群得证.
最后,证明Mα是极大正则子半群.设T是I(n,r)的正则子半群且Mα⊂T.任意取β∈T\Mα,则β∈Rα.由引理2.6知,|E(Lβ)|≥2,于是存在ε∈E(Jr)∩Lβ,使得ε∉Rα,从而Rε⊆Mα⊂T.由引理1.1可得,Rα=Rβ=βRε⊂T.因此,T=I(n,r).至此引理2.8得证.
注2.1 据文献[10]知,关于半群PORn有如下事实:(1)J0=J0POPn,J1=J1POPn.(2)对任意α∈PORn,|Hα|=2|im(α)|.此时,|POPn∩Hα|=|PRn∩Hα|=|im(α)|.(3)对任意α,β∈PORn,如果α∈POPn,β∈PRn,则αβ,βα∈PRn.(4)E(JrPOPn)=E(Jr).
引理2.9 设2≤r≤n-1,则IPOPn(n,r)=〈E(JrPOPn)〉=〈E(Jr)〉.
据文献[14]定理2可知,IPOPn(n,r)=〈E(JrPOPn)〉.再由注2.1中的(4)可得此结论.
引理2.10 设2≤r≤n-1,则对任意γ∈JrPRn,有Jr⊆〈E(Jr)∪{γ}〉.
证明 由E(JrPOPn)=E(Jr)可得γ∉E(Jr).由引理2.6知,|E(Lγ)|≥2,|E(Rγ)|≥1.取ε∈E(Lγ),η∈E(Rγ),则ε≠η.设β∈Rε∩Lη∩POPn,则由引理1.1可得,βγ∈Rβ∩Lγ,γβ∈Rγ∩Lβ(因为η∈Rγ∩Lβ,ε∈Lγ∩Rβ).由注2.1及β∈POPn,γ∈PRn可得,βγ,γβ∈JrPRn.注意到ε∈E(Lγ∩Rβ),η∈E(Rγ∩Lβ),Rβ∩POPn,Lβ∩POPn⊆JrPOPn.由引理1.1可得
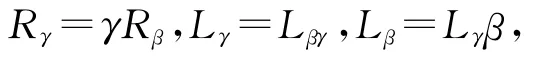
从而由注2.1,γ∈JPRn
r及引理2.9可得
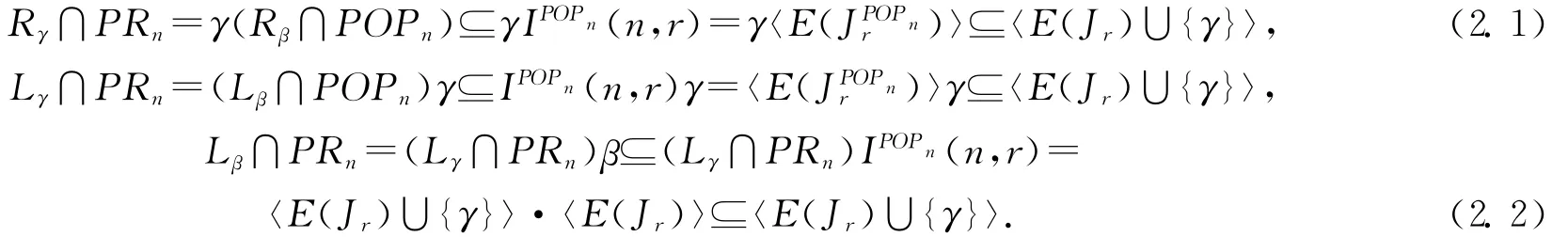
再由引理2.9可知
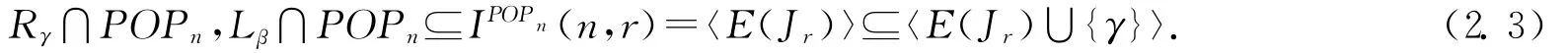
注意到
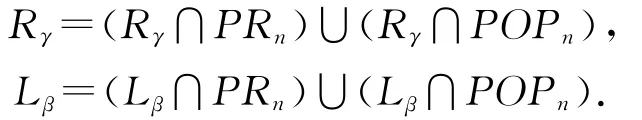
由(2.1)—(2.3)式可得
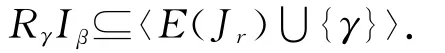
注意到ε∈E(Lγ∩Rβ).再由引理1.1可得
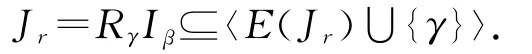
引理2.11 设2≤r≤n-1,则I(n,r)=〈Jr〉.
证明 显然〈Jr〉⊆I(n,r).注意到I(n,r)=J0∪J1∪J2∪…∪Jr.任意取α∈I(n,r),则存在0≤k≤r,使得α∈Jk.以下分两种情形证明α∈〈Jr〉:
情形1 k=0或1.由引理2.9及注2.1可得
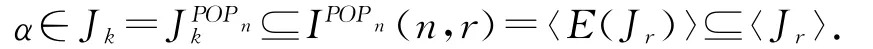
情形2 2≤k≤r.由引理2.9及注2.1可得
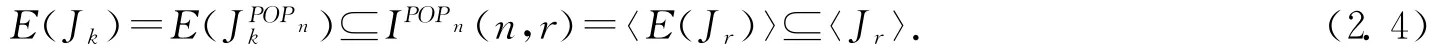
令
在金融机构“引进来”和“走出去”方面,1996年,泰京银行进入云南,这是第一家进入云南的外资银行。之后,恒生银行、汇丰银行、东亚银行、渣打银行等相继进入云南市场。到了2017年,进入云南的外资银行数量已达8家。同时,云南省金融业深入推进沿边金融综合改革,积极支持辐射中心建设,重点改革领域取得多项突破。
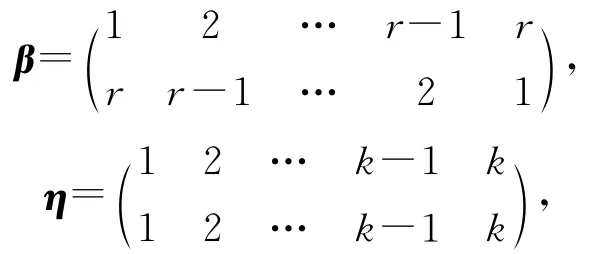
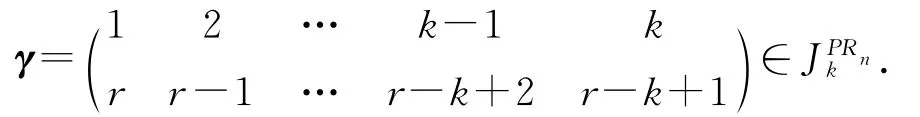
进而,由引理2.10及(2.4)式可得
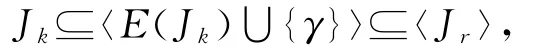
从而α∈Jk⊆〈Jr〉.综上所述,α∈〈Jr〉.由α的任意性,I(n,r)⊆〈Jr〉.因此I(n,r)=〈Jr〉.
引理2.12 设2≤r≤n-1,α∈Jr,则Nr=I(n,r-1)∪是I(n,r)的极大正则子半群.
设T是I(n,r)的正则子半群,且Nr⊂T.由I(n,r)=(n,r-1)∪⊆Nr及引理2.9,E(Jr)⊆〈E(Jr)〉=(n,r)⊆Nr⊂T.任意取β∈T\Nr,则β∈,于是由引理2.10,Jr⊆〈E(Jr)∪{β}〉⊆T,从而由引理2.11可得T=I(n,r).因此Nr是I(n,r)的极大正则子半群.
定理2.1的证明 设A1,A2,…,Am是Xn的所有基数为r的子集,其中m=.记
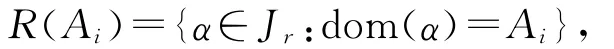
其中i=1,2,…,m,则R(A1),R(A2),…,R(Am)是Jr的一些互不相同的R-类.对任意j∈{1,2,…,m},显然有|E(R(Aj))|=1.我们用εj表示R类R(Aj)中唯一的幂等元(事实上,εj是Aj上的恒等变换).
由引理2.8,2.12可知,Mα和Nr是I(n,r)的极大正则子半群.我们将用反证法证明I(n,r)的极大正则子半群仅有定理2.1中的形式.假设S是I(n,r)的极大正则子半群,且不是定理2.1中的形式,则

否则,存在α∈Jr,使得Rα⊆Jr\S或⊆Jr\S,于是Mα或Nr是I(n,r)的包含S的正则子半群,由S的极大性可得,S=Mα或S=Nr,与S不是定理2.1中的形式矛盾.我们断言

事实上,如果存在α∈Jr,使得La⊆Jr\S.设im(α)=Ai,考察R-类R(Ai)中唯一的幂等元εi,则εi∈E(R(Ai))∩Lα,于是εi∉S,从而S∩Rεi=∅(否则,由S的正则性及引理2.4可推出,R(Ai)中唯一的幂等元εi∈S),与条件(2.5)矛盾.
我们将证明E(Jr)⊆E(S).假设E(Jr)\E(S)≠∅.任意取ε∈E(Jr)\E(S)⊆Jr.由(2.5)及(2.7)式可知,S∩Lε≠∅,S∩Rε≠∅.任意取β∈S∩Lε,γ∈S∩Rε,由引理2.4及S的正则性可得,Lβ∩E(S)≠∅,Rγ∩E(S)≠∅,进而存在η∈E(S)∩Lβ=E(S)∩Lε,ρ∈E(S)∩Rγ=E(S)∩Rε,使得η,ρ∉Hε(因为ε∉E(S)).再由引理1.1可得,ηρ∈S∩Rη∩Lρ(因为ε∈E(S),且ε∈Lβ∩Rγ=Lη∩Rρ).注意到η,ρ∈E(S),ηρ∈S,ηRηρLρ.由引理2.5可知,存在ηρ的逆元δ,使得δ∈S∩Lη∩Rρ=S∩Lβ∩Rγ=S∩Lε∩Rε=S∩Hε,从而δ是一个群元素.进而存在自然数n,使得ε=δn∈E(S),与ε∈E(Jr)\E(S)矛盾.因此E(Jr)⊆E(S).
由(2.6)式可知,S∩JrPRn≠∅.任意取γ∈S∩,由引理2.10可得Jr⊆〈E(Jr)∪{γ}〉⊆〈E(S)∪{γ}〉⊆S,从而由引理2.11可得,S=I(n,r),与S的极大性矛盾.至此定理2.1得证.
[1] YANG XIU-LIANG,LU CHUNG-HAN.Maximal properties of some subsemigroups in finite order-preserving transformation semigroups[J].Communications in Algebra,2000,28(6):3125-3135.
[2] YOU TAI-JIE.Maximal regular subsemigroups of certain semigroups of transformations[J].Semigroup Forum,2002,64(3):391-396.
[3] YANG HAO-BO,YANG XIU-LIANG.Maximal subsemigroups of finite transformation semigroups K(n,r)[J].Acta Mathematica Sinica,2004,20(3):475-482.
[4] 赵平,游泰杰,徐波.方向保序变换半群K(n,r)的极大正则子半群[J].吉林大学学报:理学版,2011,49(2):203-206.
[5] DIMITROVA I,KOPPITZ J.On the maximal regular subsemigroups of ideal of order-preserving or order-reversing transformations[J].Semigroup Forum,2011,82(1):172-180.
[6] ZHAO PING.Maximal regular subsemibands of finite order-preserving transformation semigroups K(n,r)[J].Semigroup Forum,2012,84(1):97-115.
[7] DIMIMTROVA I,FERNANDES V H,KOPPITZ J.The mmaximal subsemigroups of semigroups of transformations preserving or reversing the orientation on a finite chain[J].Publicationes Mathematicae Debrecen,2012,81(1):11-30.
[8] 罗永贵,瞿云云.半群POn中理想的非群元秩和相关秩[J].东北师大学报:自然科学版,2014(3):20-27.
[9] 吴江燕,游泰杰.保序部分变换半群POn的平方幂等元[J].东北师大学报:自然科学版,2015(1):6-11.
[10] FERNANDES V H,GOMES G M S,JESUS M M.Congruences on monoids of transformations preserving the orientation on a finite chain[J].Journal of Algebra,2009,321(3):743-757.
[11] CLIFFORD A H,PRESTON G B.The algebraic theory of semigroups[M].Providence:American Mathematical Society,1961:1-223.
[12] HOWIE J M.Fundamentals of semigroup theory[M].Oxford:The Clarendon Press,1995:1-349.
[13] FERNANDES V H.The monoid of all injective orientation preserving partial transformations on a finite chain[J].Communications in Algebra,2000,28(7):3401-3426.
[14] 张传军,朱华伟.由秩为r的幂等元生成的保向部分变换半群V(n,r)[J].西南大学学报:自然科学版,2013,35(8):72-76.
Maximal regular subsemigroups of the ideals of semigroup PORn
ZHAO Yi,YOU Tai-jie,ZHAO Ping
(School of Mathematics and Computer Science,Guizhou Normal University,Guiyang 550001,China)
Let POPnand PORnbe the partial orientation-preserving transformation semigroup and the partial orientation-preserving or orientation-reserving transformation semigroup on Xn,respectively.For an arbitrary integer r such that 2≤r≤n-1,the structures of the maximal regular subsemigroups of the semigroup I(n,r)={α∈PORn:|im(α)|≤r}are studied.Using Miller-Clifford theorem,the authors proved that I(n,r)has exactly two class of maximal regular subsemigroups,i.e.:(ⅰ)Mα=I(n,r-1)∪(Jr\Rα),α∈Jr;(ⅱ)Nr=I(n,r-1)∪,where Jr={α∈PORn:|im(α)|=r}={α∈POPn:|im(α)|=r},Rαbe the R-class ofα.
transformation semigroup;orientation-preserving;orientation-reserving;maximal regular semigroup
O 152.7 [学科代码] 110·2115
A
(责任编辑:陶 理)
1000-1832(2015)03-0044-05
10.16163/j.cnki.22-1123/n.2015.03.010
2014-03-04
国家自然科学基金资助项目(11461014);贵州省科学技术基金资助项目(黔科合J字[2013]2225号).
赵颐(1980—),男,硕士,讲师,主要从事群论和编码理论研究;游泰杰(1959—),男,教授,主要从事群论和半群理论研究.
