一类代换系统及其超空间系统

汪 威，李 健，朱晓刚，廖梦兰，陈冰冰

（1.吉林农业大学信息技术学院，吉林长春130118；2.长春工程技术学院机械系，吉林长春130117；3.吉林大学数学研究所，吉林长春130012）

一类代换系统及其超空间系统

汪 威1，李 健1，朱晓刚2，廖梦兰3，陈冰冰1

（1.吉林农业大学信息技术学院，吉林长春130118；2.长春工程技术学院机械系，吉林长春130117；3.吉林大学数学研究所，吉林长春130012）

考察了非本原代换及其诱导的集值映射的动力学性质.给出了该类代换诱导的超空间系统是Li-Yorke混沌的一个充分条件.证明了这类代换的拓扑熵为0，并且给出了这类代换诱导的集值映射具有零拓扑熵的一个充分条件.

代换；超空间系统；拓扑熵；Li-Yorke混沌

0 引言

混沌理论的研究涉及很多领域［1］.在农业科技研究中，很多实际问题都可以归结为对混沌现象的分析，如玉米病虫害的预测预报、农业灌溉用水量的预报、粮食产量的预测等等.本文所涉及的Li-Yorke混沌［2］的定义如下：

设（X，f）为紧致系统，d是X的一个拓扑度量，如果Y⊂X中任何不同两点x，y都满足：

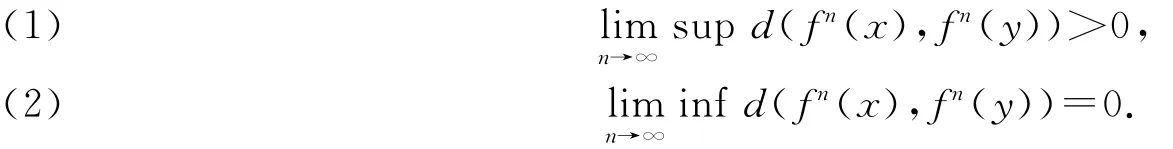
则称Y为f的Li-York混沌集.如果f有一个不可数的Li-Yorke混沌集，则称它是Li-Yorke混沌的.

文献［3］证明了有限个符号的本原等长代换诱导的子移位可能存在Li-Yorke混沌集，但一定不是Li-Yorke混沌的.文献［4］探讨了两个符号的等长本原代换存在Li-Yorke混沌的等价刻画.文献［5］给出了双符号的非本原等长代换诱导的子移位是Li-Yorke混沌的等价条件.

本文所涉及的有关超空间系统的定义及记号，详见文献［6］.

设（X，J）是一个拓扑空间，P（x）表示X的所有非空子集构成的集合，G1，G2，…，Gn是X的n个非空开集，令则所有形如B（G1， G2，…，Gn）的集合构成了空间P（x）的某个拓扑的基，这个拓扑称作Vietoris拓扑.这个拓扑空间记作（P（X），Jv），也称为（X，J）的超空间.

本文主要考察空间（X，J）的闭集类，即K（X）＝｛K∈P（X）；K是X的非空紧子集｝.

对任意A，B∈K（X），

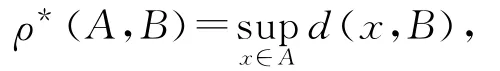
其中

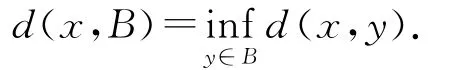
而K（X）上与Vietoris拓扑相容的Hausdorff度量定义为

设f：X→X连续.令f¯：K（X）→K（X）定义为f¯（A）＝｛f（a）：a∈A⊂X｝，我们称f¯是f到K（X）上的扩张，即f¯是K（X）上的集值映射.

由文献［6］可知，空间（K（X），H，f¯）构成一个紧致系统，称其为由底空间紧致系统（X，d，f）诱导的超空间紧致系统，简称超空间系统，简记为（K（X），f¯）.底空间紧致系统（X，d，f）简记为（X，f），称为底系统.?

1 符号空间和等长代换

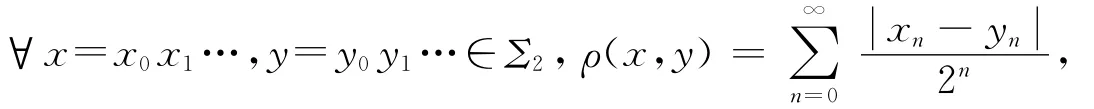
则ρ是Σ2上的度量.称度量空间（Σ2，ρ）为（具有两个符号的）单边符号空间，或者称做符号空间.

定义1.1 设η为符号空间Σ2上的等长代换，定义为

并且满足条件a0＝0，及存在i＞0，使得ai＝1.则η在Σ2中有一个以0开头的不动点，记作u.

设Xη为u在移位映射σ作用下轨道的闭包，即

令f＝σ｜X，则f：Xη→Xη为σ的子移位，称其为由η诱导的子移位.

定义1.2 如果0≺η（1），即η（1）包含0，则称η是本原的；否则，称η是非本原的.

下面，我们假设f是由等长代换η诱导的代换子移位，并且给出如下条件：

（C）存在不同的s1，s2，t∈｛0，1，…，n－1｝，使得as1≠bs1，as2≠bs2，并且at＝bt.

引理1.1［5］设η是非本原代换，则下述条件等价：

（1）若η满足条件（C）；

（2）f是Li-Yorke的；

（3）f有Li-Yorke对.

以下我们总假设η是非本原的等长代换.（Xη，f）是由η诱导的代换系统子移位，（K（Xη），f¯）是其诱导的超空间系统.

2 等长代换与Li-Yorke混沌

定理2.1 若η满足条件（C），则（K（Xη），f ）是Li-Yorke混沌的.

证明 由于η满足条件（C），则由引理1.1可知η是Li-Yorke混沌的，即存在不可数的Li-Yorke混沌集Y⊂Xη.

任取｛x，y｝⊂Y，如果｛x，y｝是（Xη，f）中的Li-Yorke对，则满足条件

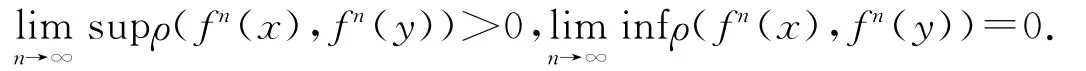
而｛｛x｝，｛y｝｝是（K（Xη），f¯）中的点对，其对应的Hausdorff度量为

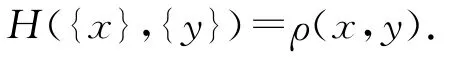
于是，对上述｛｝x，｛｝y，有

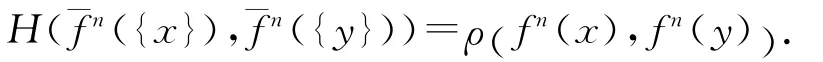
由此可得出如下结论：

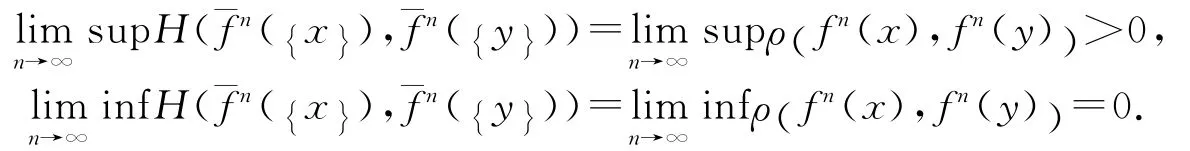
即｛x｝与｛y｝是（K（Xη），f）中的Li-Yorke点对.

令K（Y）＝｛｛x｝；x∈Y｝，则K（Y）⊂K（Xη）.根据上述证明可知，K（Y）是（K（Xη），f）的不可数的Li-Yorke混沌集，因此（K（Xη），f）是Li-Yorke混沌的.

3 等长代换与拓扑熵

定理3.1 η诱导的代换子移位的拓扑熵为0，即h（f）＝0.

证明 设A为出现在u中的长度为n的符号段，r（A）为A中所含0的个数，则由文献［5］中断言3.1及断言3.2可知

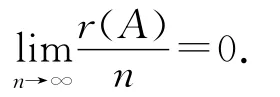
记

则

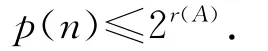
由文献［7］可知，子系统（xη，f）的拓扑熵

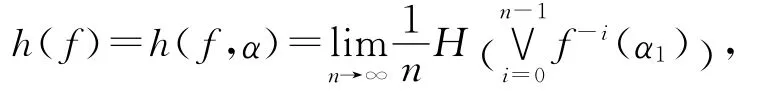
即

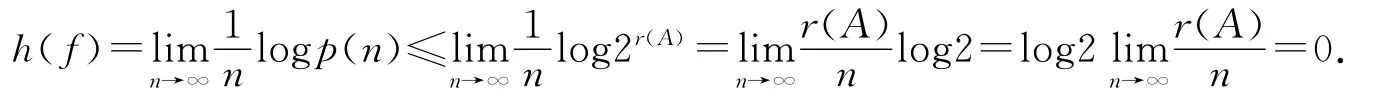
定理3.2 若η不满足条件（C），则h（f¯）＝0.

证明 由文献［5］知，若η不满足条件（C），则Xη中只有两个点，即v＝111…和u＝011…，它们都是不动点.因此，K（Xη）＝｛｛u｝，｛v｝，｛u，v｝｝是一个三点构成的离散拓扑空间.进而，f¯的（n，ε）-张成集和（n，ε）-分离集都是有限集.那么，

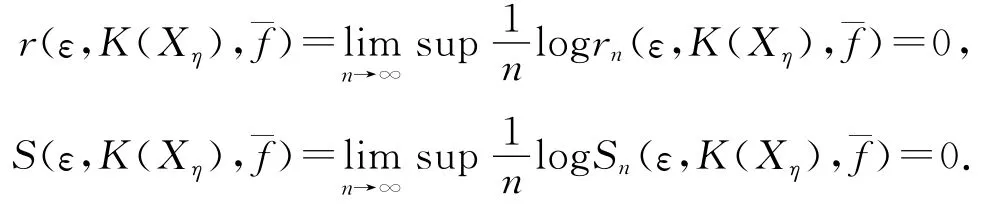
由此可知

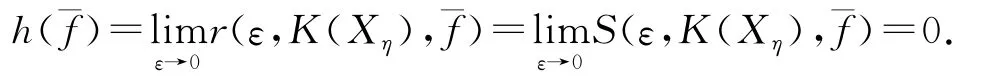
［1］ 尹社会，张勇，张付臣，等.基于Lorenz系统的强迫Lorenz混沌系统的动力学研究［J］.东北师大学报：自然科学版，2014，46（1）：42-47.

［2］ LI TIANYAN，YORKE J A.Period three implies chaos［J］.The Amer Math Monthly，1975，82：985-992.

［3］ BLANCHARD F，DURAND F，MAASS A.Constant-length substitutions and countable scrambled sets［J］.Nonlinearity，2004，17：817-833.

［4］ 廖公夫，范钦杰，王立冬.一类本原代换与混沌集［J］.中国科学：A，2008，38：469-476.

［5］ LIAO GONGFU，WANG WEI，FAN QINJIE.A class of non-primitive substitutions and chaos［J］.Chinese J Contemp Math，2009，30（2）：133-138.

［6］ 廖公夫，王立冬，范钦杰.映射迭代与混沌动力系统［M］.北京：科学出版社，2013：179-180.

［7］ 周作领.符号动力系统［M］.上海：上海科技教育出版社，1997：25-27.

A class of substitution systems and the hyperspace systems

WANG Wei1，LI Jian1，ZHU Xiao-gang2，LIAO Meng-lan3，CHEN Bing-bing1
（1.Information Technology College，Jilin Agricultural University，Changchun 130118，China；2.Department of Mechanical Engineering，The Institute of Changchun Engineering Technology，Changchun 130117，China；3.Institute of Mathematics，Jilin University，Changchun 130012，China）

As an important component of nonlinear science，the research on dynamical system has penetrated into many problems of agricultural production，such as prediction of corn yield and research on ecological difference equation.In this paper，we investigated dynamical properties for non-primitive substitution and the set-valued maps induced by the substitution.We gave a sufficient condition for the set-valued maps to be Li-Yorke chaotic，proved that the topological entropy of the substitution is zero，and gave a sufficient condition for the set-valued maps to have 0topological entropy.

substitution；hyperspace system；topological entropy；Li-Yorke chaos

O 189 ［学科代码］ 110·31

A

（责任编辑：陶 理）

1000-1832（2015）03-0009-03

10.16163／j.cnki.22-1123／n.2015.03.003

2014-07-07

吉林省科技发展计划项目（20140204045NY；20130522110JH）；吉林省教育厅“十二五”科学技术研究项目（2014第468号）；吉林农业大学科研启动基金资助项目（201310）.

汪威（1981—），女，博士，讲师，主要从事拓扑动力系统研究.