YKK中型高压异步电动机换热分析与冷却器优化
2015-06-27温嘉斌郑军于喜伟
温嘉斌, 郑军, 于喜伟
(1.哈尔滨理工大学电气与电子工程学院,黑龙江哈尔滨150080;2.南阳防爆电机厂,河南南阳473000)
YKK中型高压异步电动机换热分析与冷却器优化
温嘉斌1, 郑军1, 于喜伟2
(1.哈尔滨理工大学电气与电子工程学院,黑龙江哈尔滨150080;2.南阳防爆电机厂,河南南阳473000)
为了提高电机的散热性能,改善电机的温升条件,本文采用数值分析的方法对电机冷却器的冷却性能加以优化。对于YKK结构的封闭式交流异步电动机,因其结构特点,温升一直是设计时需要关注的重点问题之一。首先,以YKK450-4、800 kW中型高压异步电机为例,建立电机冷却器的三维物理模型和数学模型,给出假设条件和边界条件,并进行数值分析,得到了冷却器的流体场和温度场是分布云图;其次,通过改变档风板的个数及位置、增加导风板并改变其位置,找到其最优值;最后,对冷却器进行重新建模,经过数值分析发现冷却器的性能有了明显的改善,为以后冷却器的优化设计提供理论依据。
中型高压异步电动机;冷却器;流体场;温度场;优化设计
0 引 言
YKK系列中型高压异步电动机广泛应用于冶金、电力、化工及水处理等场合。该系列电机具有高效、节能、起动力矩大、过载能力强、噪音低、振动小及运行可靠等特点。电机运行的可靠性是考察电机性能好坏的重要指标,而对电机运行可靠性的评判又主要体现在电机运行过程中的温升问题。电机内温升过大,会导致绝缘出现分层、脱壳、老化等现象,从而使绝缘的介电性能下降引起绝缘的损坏,引发电机内部的各种放电、短路故障,最终导致电机烧毁[1]。通过分析电机的实际运行状态,准确描述电机内各部件温度场的分布,为电机故障的实时预警和诊断提供可靠的依据;并还可以与一些优化设计理论相结合。在冷却器的优化设计中可以采用两种方法。一种是做风洞实验[2],其可信度高但是成本较大;另一种方是利用计算机做仿真分析来对冷却器进行优化设计。本文采用第二种方法,这样不但可以节约生产成本,还可以减少样机的制造周期,具有重要的意义。
1 冷却器物理模型与数学模型
YKK450-4、800 kW电动机通风结构如图1所示。
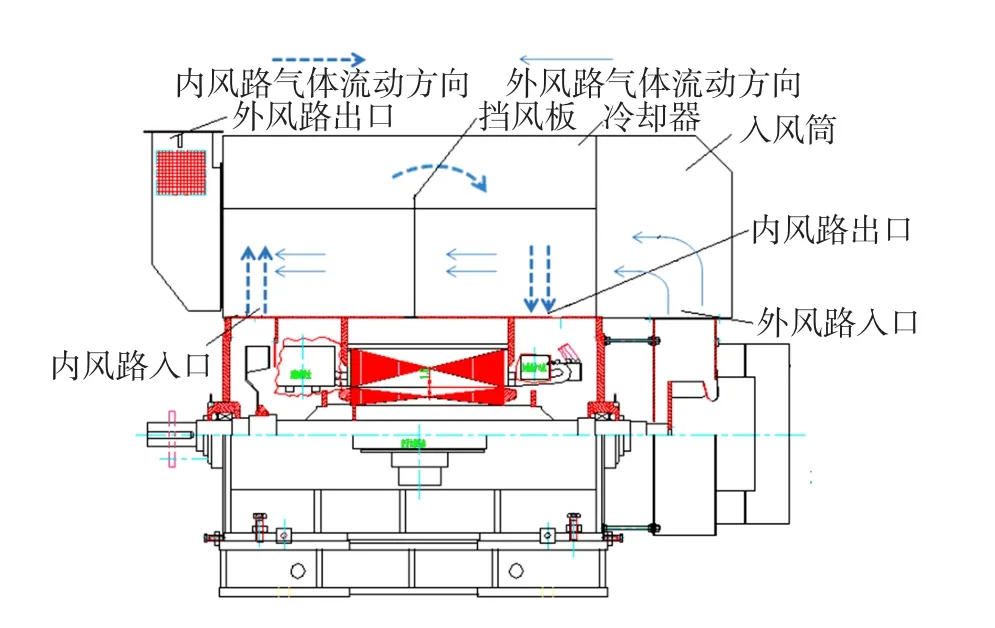
图1 电机通风结构Fig.1 Ventilation system of them otor
图1 所示电机内风路采用密闭循环结构,内部安装挡风板对流体流动方向进行约束,在电机左侧安装一个离心式风扇,通过离心式风扇产生足够大的压强迫使内风路气体进行循环流动。内风路气体依次经过定子端部、轴向通风沟、转子径向通风沟、气隙、定子径向通风沟、内风扇、冷却器,最后回到定子端部形成一个封闭的循环系统。图中虚线箭头所指方向为内风路气体的流动方向。为了将内风路气体冷却,在电机外部安装离心式风扇,使温度较低的大气进人冷却管从而达到冷却内风路气体的目的。外风路冷却气体的流动方向为大气、外风扇、冷却器人风筒、冷却管最后回到大气。图中实线箭头所指方向为外风路气体流动方向。
1.1 冷却器区域流体场物理模型
本文电机的冷却器有713根冷却管,冷却管排列示意图如图2所示。

图2 冷却管排列方式Fig.2 Cooling arrangement
冷却器由冷却管、人风筒、挡风板组成。本文中将对冷却器的挡风板和人风筒进行优化设计,将挡风板的个数由1个增加到3个,在人风筒处增加导风板并且改变斜板的角度,从而减小涡流的产生。冷却器系统的整体模型如图3所示。

图3 冷却器物理模型Fig.3 Physicalmodel of cooler
1.2 基本假设和边界条件
1.2.1 基本假设
1)计算区域内的雷诺数很大,流动属于湍流,即采用湍流模型[7];
2)常压下空气冷却的电机,忽略流体域内流体的浮力和重力的影响[7];
3)流体流速远小于声速,即把电机内流体作为不可压缩流体处理[7];
4)仅研究冷却器内流体场与温度场的稳定状态,即定常流动,因而方程中不含有时间项[8]。
1.2.2 边界条件
1)外风路人口速度为4.7 m/s(人口处5个点速度的平均值),人口温度为22.0℃(室温),采用速度人口;外风路出口采用压力出口;
2)内风路人口速度为6.0 m/s(人口处测出3个点速度的平均值),人口温度为80.0℃(人口处测量8个点温度的平均值),采用速度人口;内风路可以计算出电机外壳表面的对流换热系数为30W/(m2·k)。
1.3 冷却器区域流体场数学模型
流体流动所遵循的物理定律是建立流体运动基本方程组的依据。这些定律包括质量守恒、能量守恒和动量守恒[3]三大定律。
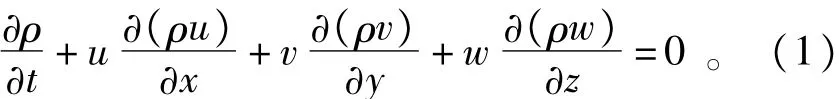
质量守恒方程为出口采用压力出口;
3)所有流体和固体的交界面设置为藕合壁面,冷却器外壳和外界空气对流换热,根据电机外壳内壁的风速v(m/s)和电机外壳表面的温度θ(K),即
动量守恒方程为
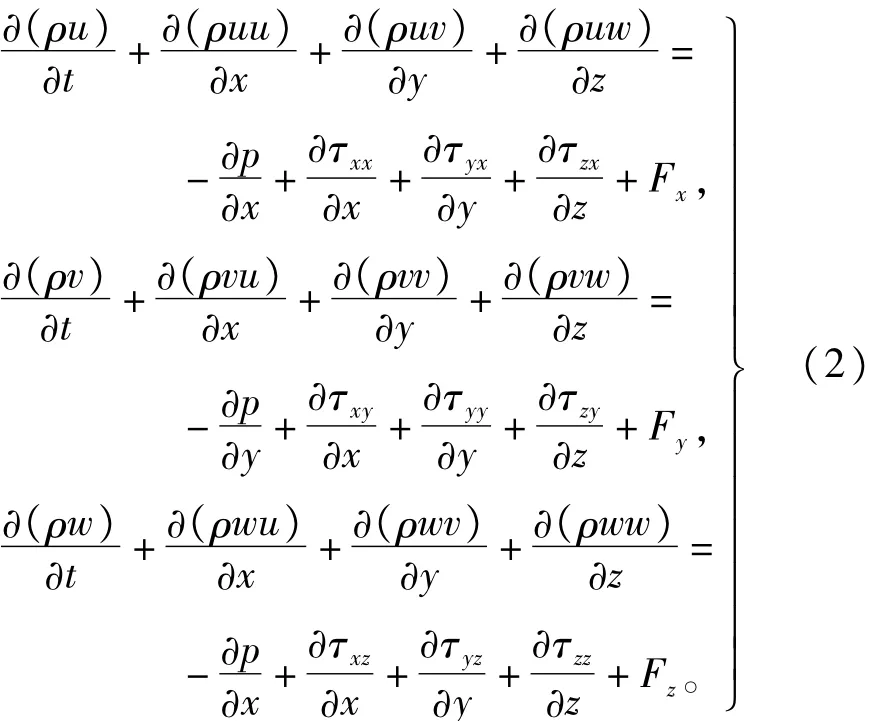
式中:p为流体微元体上的压力;τxx、τxy和τxz为粘性应力τ沿x、y和z方向的分量;Fx、Fy和Fz为微元体上的体积力。
因为本文设计到温度场计算,还需要能量守恒方程和牛顿冷却定律及表面传热系数。
能量守恒方程为
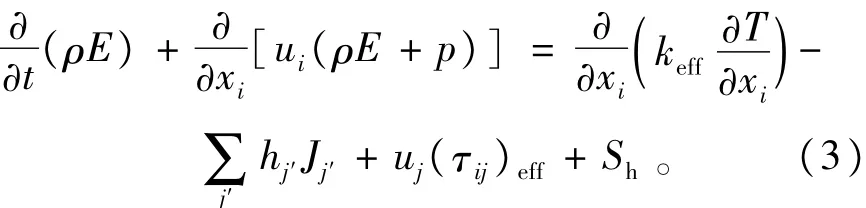
式中:keff=kt+k为有效导热系数;Jj'为组分j'的扩散系数动能耗散率;方程右边为导热项、组分扩散项和粘性耗散项;Sh是化学反应热和其它体积热源。
牛顿冷却定律表达式[4,10]为
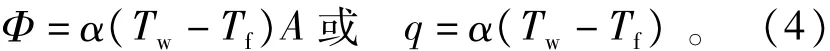
式中:Φ为单位时间通过面积A对流热流量;Tw为固体表面绝对温度;T为流体平均温度;A为传热表面积;q为对流换热热流面积;α为对流传热系数[W/(m2·K)]。
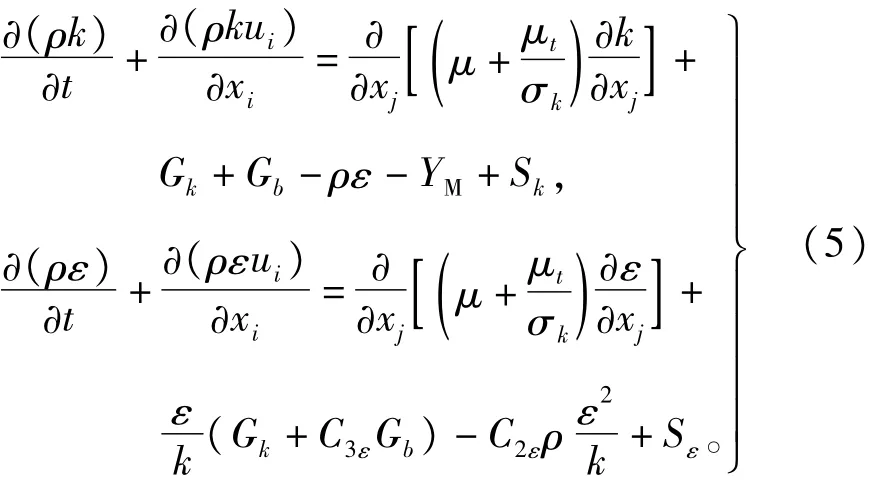
在Fluent中进行数值分析时,采用标准模型,其湍流方程[5]为式中:k为湍动能;ε为湍动能耗散率;μi为i方向速度;μ为动力粘度;Gk为由于平均速度梯度引起的湍动能k的产生项,Gb是由于浮力引起的湍动能k的产生项,YM代表可压湍流中脉动扩张的贡献,Sk和Sε为自定义的源项;μt为湍动粘度[6],可以表示成k和ε的函数,即μt=ρCμ在Fluent中取经验值C1ε=1.44,C2ε=1.92,C3ε=0.09;湍动能k与耗散率ε的湍流普朗特数分别为σk=1.0,σε=1.3。
2 冷却器区域流体场温度场耦合计算
2.1 原冷却器区域流体场与温度场计算
由于冷却器有713根冷却铝管且整体尺寸较大,在进行网格剖分和数值计算时对计算机的内存和运算有很大的要求,因为冷却器的结构是对称的,所以本文选取1/9的冷却器进行建模计算分析。整个计算区域剖分约290万个单元,370万个节点。因为本文要对冷却管的表面散热情况进行分析,所以对其采用结构化网格剖分,剖分后的模型如图4所示。
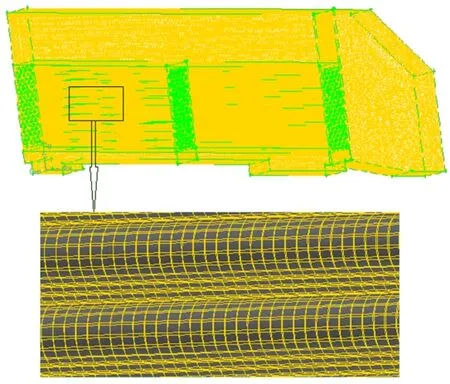
图4 计算区域网格剖分Fig.4 Computational domain mesh dissection
剖分、定义边界条件后,数值计算后得到冷却器的温度云图如图5所示、速度矢量图如图6所示、流体迹线图如图7所示和外管壁对流传热系数如图8所示。
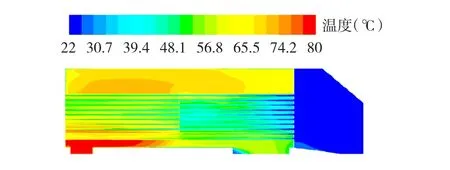
图5 截面的温度图Fig.5 The temperature distribution of a section
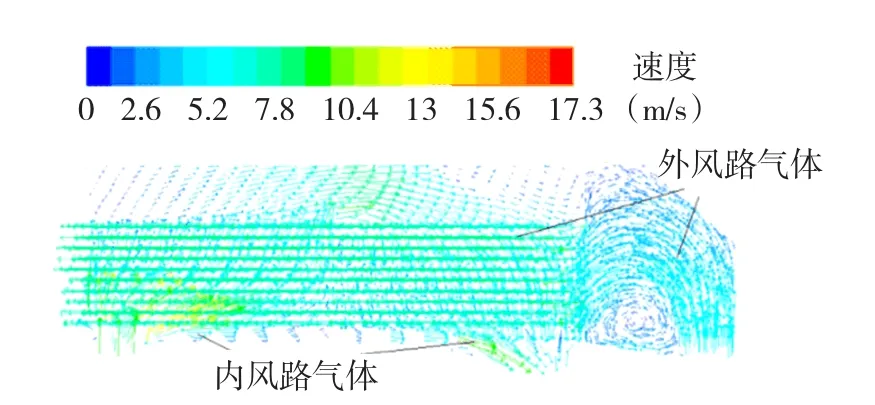
图6 截面的速度矢量图Fig.6 The vector velocity of a section
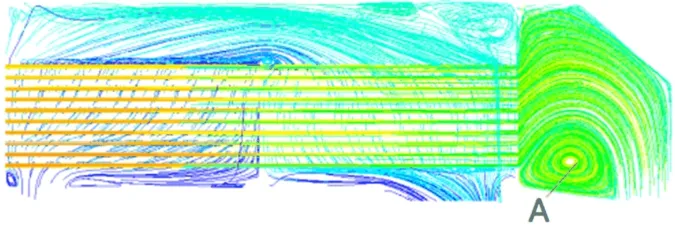
图7 截面的流体迹线图Fig.7 Computational domain mesh dissection
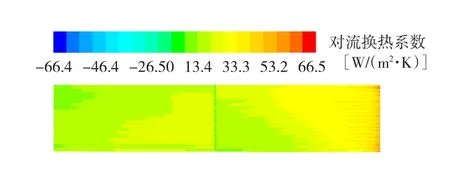
图8 铝管内表面对流传热系数图Fig.8 A lum inum inner surface convective heat transfer coefficient
从图5中可以看出内风路人口温度最高达到80.0℃,经过与冷却管接触,在内风路出口的温度降低到52.5℃,外风路的低温气体经过冷却器后由22.0℃升高到51.0℃。但是从冷却管温度分布图可以看出其温度升高的不是很多,说明冷却空气没有得到充分的利用。从图6中看出人风筒区域的流体进人冷却管后流速增大,这是由于流体流动的截面积突然变小造成的,流量不变,流速增大。从图7中看出A处有明显的涡流出现,这将会导致能量损失加大并且产生很大的噪音[9],但是挡风板处回流的存在有助于热空气与冷却管的接触,使内风路温度降低。从图8中可以看出在内、外风路人口处的对流传热系数比较大,这是因为空气刚进人冷却管,流速突然增大,流速增加又会使流体内部相对运动加强,从而使对流作用加强,也就使对流换热加强,对流换热系数增大[10]。
为验证数值分析合理性,对YKK450-4、800 kW电机进行试验对比,使电机工作在额定功率下,达到稳定运行时,测得多组数据来进行求取平均值作为实验数据。其中外风路出口处的风速共测15个点。表1中给出的试验数据与数值计算结果的对比图。
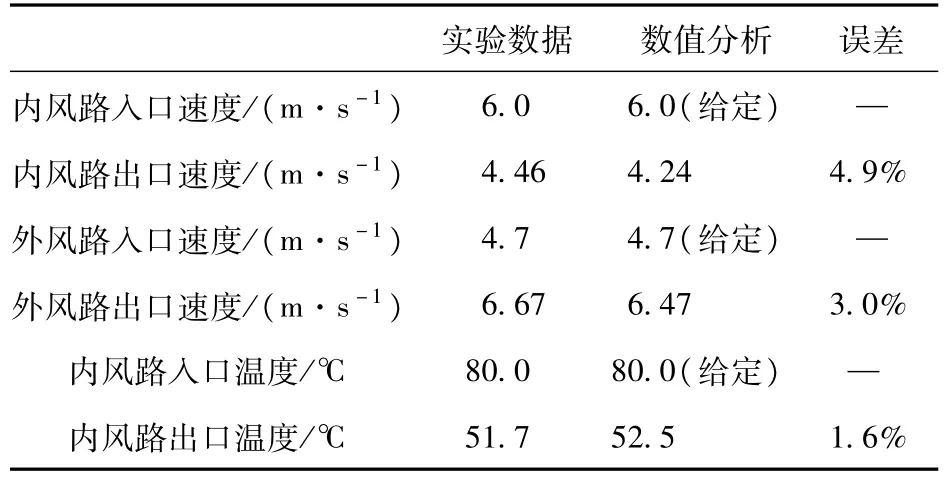
表1 实验与数值分析对比Table 1 The contrast of experience and numerical analysis
2.2 对冷却器优化设计计算
从原冷却器模型中可以看到冷却管的冷却空气没有被充分的利用;经过分析后,增加导风板来均衡分配每层管的流量;减少人风筒直角的使用可以明显减少涡流的产生。基于此本文对冷却器进行优化设计。改变结构后的冷却器物理模型如图9所示。将挡风板的个数由1块变为3块,即增加挡板1和3,将原挡板上移变为挡板2,对各个部分的优化设计进行分别做如下阐述。
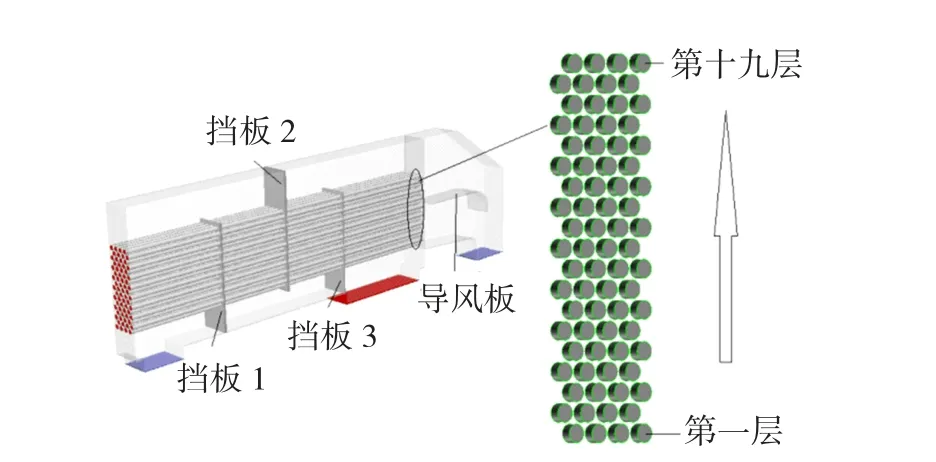
图9 优化后的模型Fig.9 Themodel of optim ization
2.2.1 对导风板的优化
增添一个导风板,并将导风板在原有的基础上分别上移20、40、60和80 mm。分别建模进行数值分析计算,得出上移40mm时各层流量分配比较均匀。各层流量分配对比图如图10所示,内风路出口温度对比如图11所示。从图10中可以看出改进后冷却管人口的流量分配更加均匀,这样会使得管壁散热效果更好。在图11中能够看出导风板上移40mm时内风路出口有所降低,温度为51.5℃。
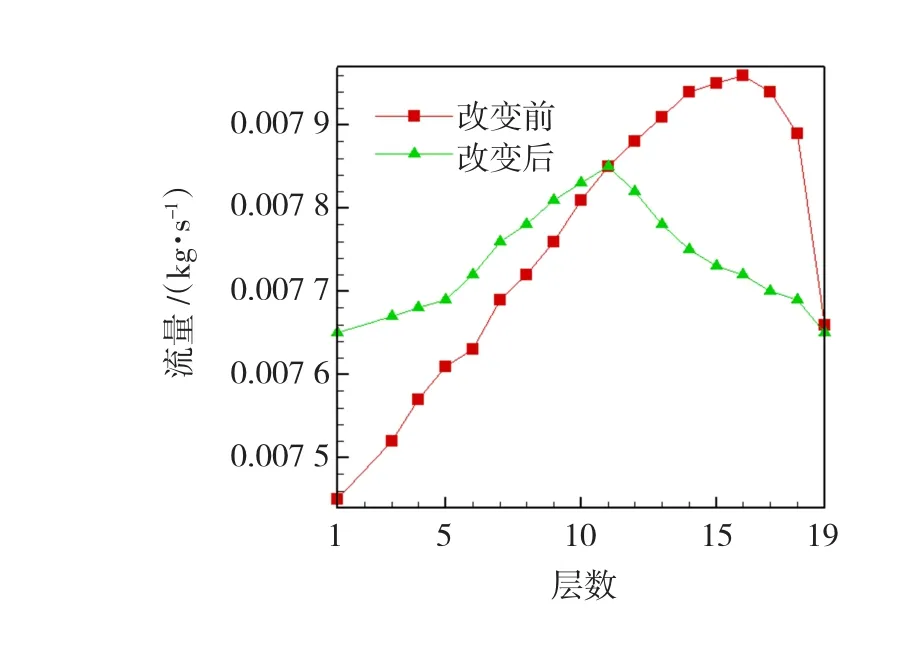
图10 各层流量分配对比Fig.10 Contrast flow distribution layers
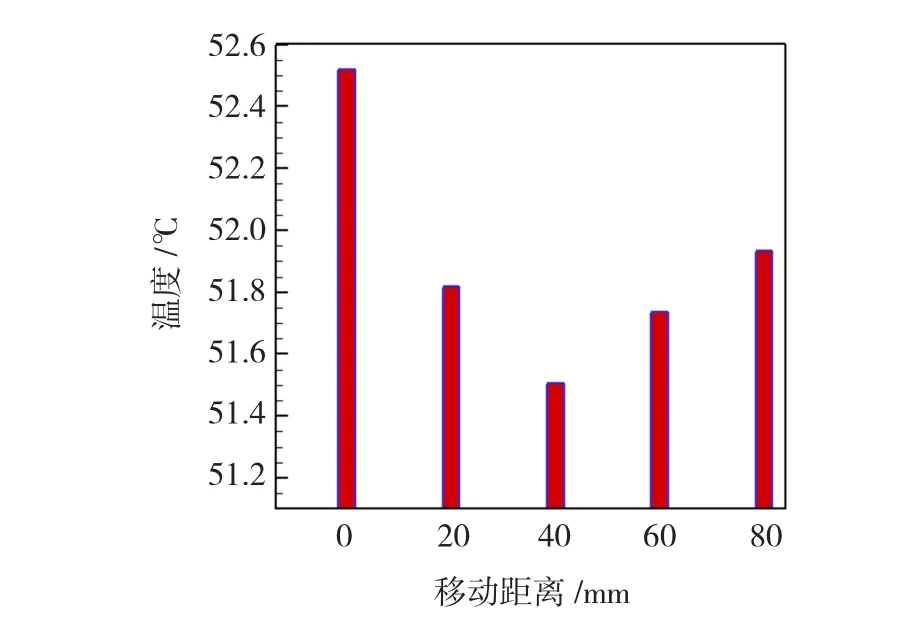
图11 内风路出口温度对比Fig.11 Contrast of the inner air duct outlet temperature
再将导风板在原有的基础上分别外移10、20、30和40 mm。重新建模进行对比分析得出将导风板外移30mm时温度下降教明显,原因是改变导风板的位置后,从流体迹线图进行对比分析得出将导风板外移30 mm时使涡流明显减少,能量损失减少,进而温度下降,其值为50.8℃。内风路出对温度对比图如图12所示。
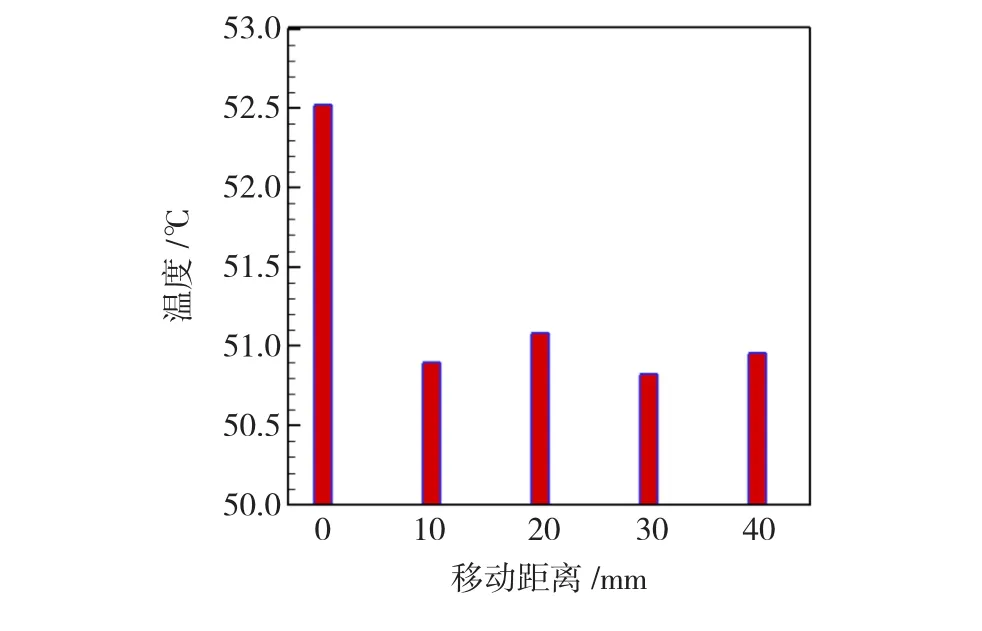
图12 导风板右移温度对比图Fig.12 Contrast of temperature of the wind deflector right
2.2.2 对挡板的优化
优化前的冷却器模型只有一块挡风板,内风路出来的风没有得到充分的冷却,所以将挡风板改成3块,如图9所示。改变模型后进行数值计算分析,内风路的出口温度有明显的降低,改进前后温度对比图如图13所示。从图中可以看到温度降到50.2℃。但是通过数值分析后发现内风路人口所需要的静压会提高,所以要想办法将内风路人口所需静压强减小。在图9中将3块挡板标号以便区分,首先挡板3的位置保持不变,改变挡板1的位置,并且使挡板2始终处于挡板1和3的中间位置。将挡板1从内人口的右端点依次右移70、140和210mm。计算后发现改变挡板的位置对内风路出口温度几乎没有影响,只对内风路人口所需要的静压有很大的影响。对比图如图14所示。从图中看出将挡板1右移210mm时所需要的静压强最小为2 776.8 Pa。
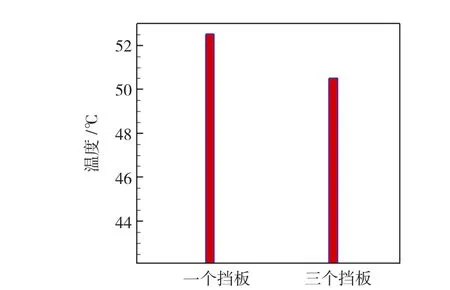
图13 增加挡板个数温度对比图Fig.13 Contrast of tem perature at increased the number of baffles
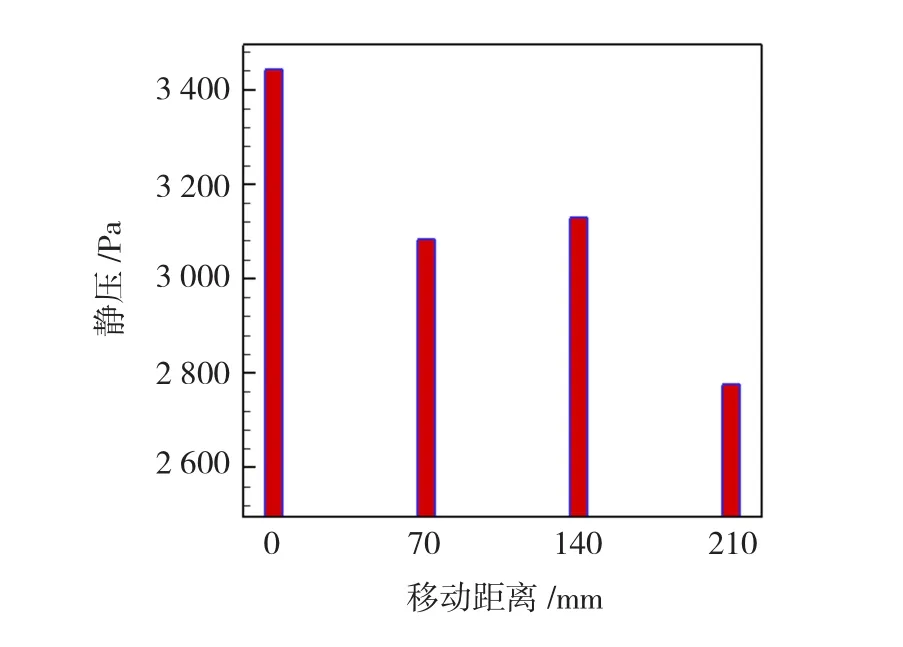
图14 减静压对比图Fig.14 Contrast of the less static pressure
2.2.3 对冷却器直角形状的优化
流体在流动过程中,除了与管壁之间的摩擦阻力以外,由于管道形状、尺寸变化或发生某些障碍时,流体质点之间的相对速度、方向将发生变化,碰撞将加剧,便产生一定的能量损失[10]。
以压力降的形式表示为
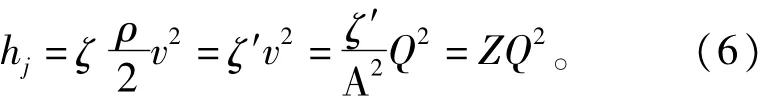
式中:ζ表示局部阻力系数;ζ'表示风阻系数;Z表示风阻。
电机冷却系统内,局部损失占很大比重,因此局部阻力系数ζ对电机通风是必不可少的。本文将图中画圈的M处的斜板用M'处的圆弧板来代替,这样可以使ζ降低,从改进后的流体迹线图中能够看到M'处的涡流有明显的减少。斜板改变前后的对比图如图15所示。
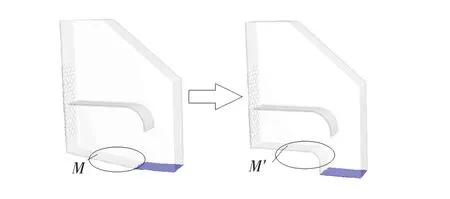
图15 改变斜板形状对比图Fig.15 Contrast of changed the inclined p late shape
2.3 对冷却器综合优化设计结果分析
经过上文对冷却器结构的改变,按照各个部分的最优值方法设计出冷却器的物理模型,如表2所示。在Fluent数值迭代后,得到温度云图如图16所示、速度矢量图如图17所示、流体迹线图如图18所示和内管壁传热系数如图19所示。

表2 整体优化前后对比Table 2 The contrast result of holistic optim ization
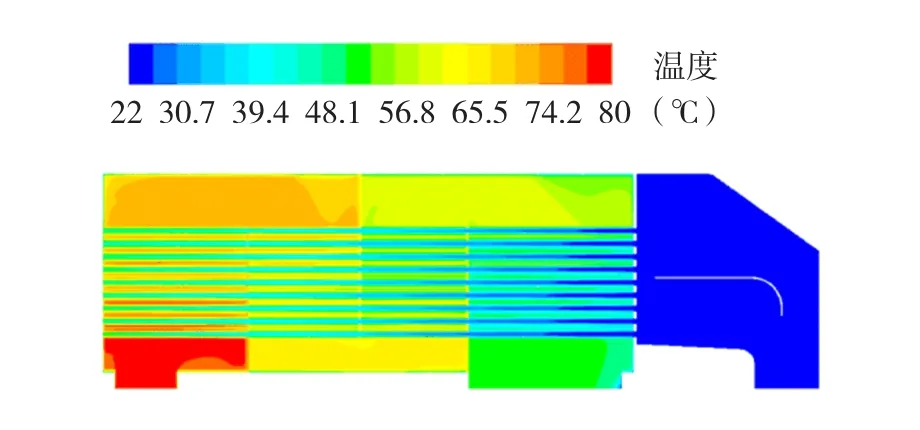
图16 改进后截面温度图Fig.16 Improved of tem perature distribution of a section
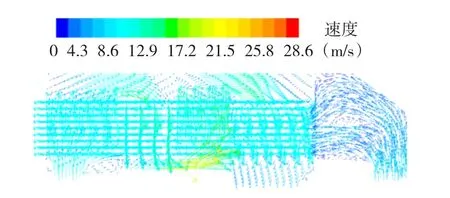
图17 改进后速度矢量图Fig.17 Improved of vector velocity of a section

图18 改进后的流体迹线图Fig.18 Improved of fluid traces of a section
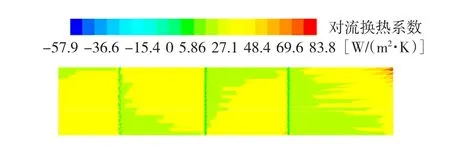
图19 改进后的内管壁传热系数Fig.19 Improved of alum inum inner surface convective heat transfer coefficient
改进后冷却器内风路出口温度为49.2℃,外风路出口温度升高到54.9℃,内风路人口所需要的静压为2 776.8 Pa。内风路出口的温度较改变前降低了3.3℃,外风路出口的温度升高了3.9℃,较原结构有明显的改善。从速度矢量图中可以看到改进后冷却管中的流速大于改进前的,这是因为将人风筒中的涡流减少,从而使能量损失降低,速度增大,流速的增大会使得冷空气快速流动带走更多的热量。从流体迹线图中可以看到A'上下处的涡流明显减少,这有助于减少噪音和能量的损失。通过管壁传热系数分布图中我们可以看到增加挡板的个数使得热空气与冷却管进行对流换热的次数增加,热空气和冷却管能够更加充分接触,平均的对流传热系数较改变模型前有很大的提高,从而将内风路出口温度降的更低。
3 结 论
1)通过数值分析计算得到冷却器内外风路的流体场和温度场分布,从中可以看出人风筒涡流较大,能量损失大、噪音大。经改进后涡流减少,能量损失减少,冷却管中流速提高,使冷却管能够带走更多的热量,从而提高冷却器的散热性能;
2)改变挡风板的个数能够明显的改善内风路出口的温度,并且通过改变挡板的位置能够减少内风路人口所需要的静压;
3)通过本文分析得出,在以后设计模型时要避免直角和尖角的出现尽量用平滑的圆弧来代替,这样可以减少涡流的产生。
[1] 张新波,许承千,杨红.电机内冷却器换热效果的综合计算[J].电工技术学报,1998,8:8-9. ZHANG Xinbo,XU Chengqian,YANG Hong.Consolidation of themotor cooler of effectof heat transfer[J].Transaction of China Electrotechnical Society,1998,8:8-9.
[2] NAKAHAMA Takafumi,BISWAS Debasish,KAWANO Koichiro,et al.Improved cooling performance of largemoors using fans[J]. IEEE Transactions on Energe Conversion,2006,21(2):324 -331.
[3] 王福军.计算流体动力学分析CFD软件原理与应用[M].北京:清华大学出版社,2004:7-10.
[4] 孟大伟,温嘉斌,魏永田,等.双层筒结构灯泡式水轮发电机热交换与肋优化计算[J].电工技术学报.1998,13(1):18-22. MENG Dawei,WEN Jiabin,WEIYongtian,et al.Heat exchange and rib optimal calculation for bulb tubular turbine generator with layer structure[J].Transaction of China Electrotechnical Society,1998,13(1):18-22.
[5] 江帆,黄鹏.Fluent高级应用与实力分析[M].北京:清华大学出版社,2008:13-15.
[6] 陶文铨.数值传热学[M].第2版.西安:西安交通大学出版社,2001:348-350.
[7] 路义萍,丰帆,孙明琦,等.同步电机定子与气隙流场数值计算与分析[J].电机与控制学报,2011,15(8):47-51. LU Yiping,FENG Fan,SUN Mingqi,et al.Numerical calculation and analysis of fluid flow field of stator and gap of a synchronousmachine[J].Electric Machines and Control,2011,15(8): 47-51.
[8] 李伟力,杨雪峰,顾德宝,等.多风路空冷汽轮发电机定子内流体场与传热藕合计算与分析[J].电工技术学报,2009,24 (12):24-30. LIWeili,YANG Xuefeng,GU Debao,et al.Stator windy road in the air-cooled heat transfer fluid field and coupling calculation and analysis[J].Transaction of China Electrotechnical Society,2009,24(12):24-30.
[9] 孟大伟,何金泽,夏云彦.箱式YJKK紧凑型中型高压电动机全域流体预测[J].电机与控制学报,2012,16(12):66-71. MENG Dawei,HE Jinze,XIA Yunyan.All-around fluid forecast research of the compactmedium size high voltagemotor[J].Electric Machines and Control,2012,16(12):66-71.
[10] 魏永田,孟大伟,温嘉斌.电机内热交换[M].北京:机械工业出版社,1998:146-148,190-205.
(编辑:刘琳琳)
Heat transfer analysis and cooler optim ization of YKK medium size high voltage asynchronousmotor
WEN Jia-bin1, ZHENG Jun1, YU Xi-wei2
(1.College of Electrical&Electronic Engineering,Harbin University of Science and Technology,Harbin 150080,China; 2.Nanyang Explosion Protection Group Co.,LTD,Nanyang 473000,China)
In order to improve the thermal dissipating performance of themotor and to improve the conditions of themotor temperature rise,a numerical analysismethod was applied to optimize the cooling performance of the motor cooler.For AC induction motor YKK closed structure,because of its structural characteristics,the temperature rise is one of key points of the design that is concerned.Firstly,taking a YKK450-4,800kW medium size high voltage asynchronousmotor was taken as an example.By creating its3D physical andmathematicalmodel of cooler of themotor and giving its basic assumptions and boundary conditions according to CFD theories,the fluid field and temperature field were calculated and analyzed,and their contours of cooler were shown.Secondly,by changing the numbers and the positions of the windshields,increasing the deflector and change its position,its optimal valueswere got.Finally,the cooler was remodeled.Numerical analysis shows that the performance of cooler is significantly improved,which provides theoretical basis for optimizing future design of cooler.
medium size high voltage asynchronousmotors;cooler;flow field;temperature field;optimal design
10.15938/j.emc.2015.09.005
TM 301.4
A
1007-449X(2015)09-0033-07
2014-05-21
国家自然科学基金(51275137)
温嘉斌(1961—),男,博士,教授,研究方向为电机冷却技术、电机及电机控制;郑 军(1989—),男,硕士研究生,研究方向为电机多物理场藕合分析计算;于喜伟(1986—),男,博士,工程师,研究方向为高压异步电机设计。
温嘉斌
