一类三阶两点边值问题正解的存在性和唯一性
2015-06-27庄国华武晨
庄国华,武晨
(江苏联合职业技术学院南京分院,江苏南京210019)
一类三阶两点边值问题正解的存在性和唯一性
庄国华,武晨
(江苏联合职业技术学院南京分院,江苏南京210019)
利用偏序集上的不动点定理证明了一个三阶两点边值问题:
正解的存在性和唯一性,并证明了该正解是严格单调递增的。
偏序集;边值问题;正解
Abstract:In this paper,we consider a third-order two-point boundary value problem:
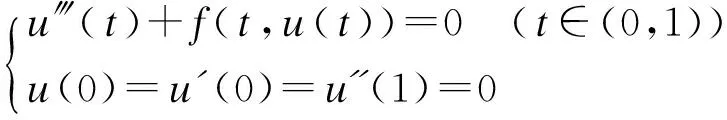
with the help of a fixed-point theorem in partially ordered sets,and obtained sufficient conditions for the existence and uniqueness positive solution to the above boundary value problem.The result showed that this solution is strictly monotonic increasing.
Key words:partially ordered set;boundary value problem;positive solution
0 引言
三阶微分方程在应用数学和应用物理学中有很重要的应用,它可以描述扰度弯曲的梁有固定或者改变交叉的部分及电磁波的传播等[1]。近来,三阶边值问题也受到了广泛的关注,同时也取得了一系列重要结果[2-7]。在文献[6]中,作者通过应用锥上的不动点定理得出三阶边值问题
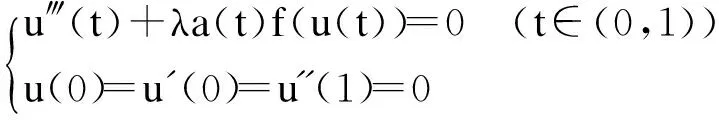
正解的存在性和多解性;在文献[7]中,作者应用线性算子的特征值理论得出文献[6]中边值问题正解的存在性。然而,以上的研究中绝大部分是通过利用锥上的不动点定理或者上下解的方法来证明解的存在性以及多解性,但利用偏序集上的不动点定理来证明解的存在性和唯一性结果相对较少。
本文正是利用偏序集上的不动点定理来证明边值问题:
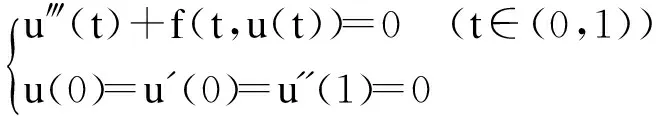
(1)
正解的存在性和唯一性,并证明了该正解还是严格单调递增的。
1 预备引理
引理2[9]假设E满足引理1中的条件,且(E,≤)满足:对于x,y∈E,存在z∈E,使得x和y均可与z相比较,则不动点是唯一的。
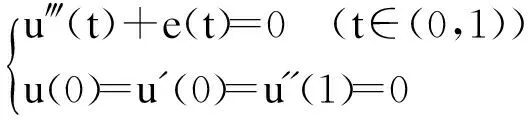
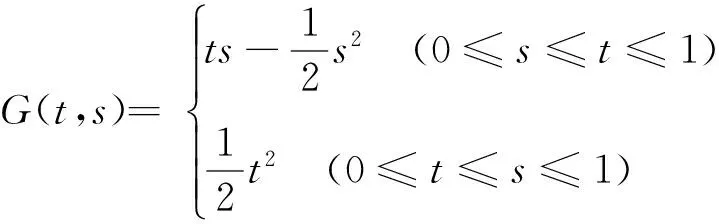
从而由引理3,可得:
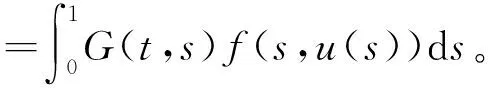
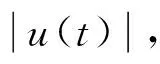
本文假设以下条件成立:
(H1)f(t,u(t))≠0,其中t∈Z⊂[0,1],μ(z)>0(μ指的是Lebesgue测度)时,f:[0,1]×[0,+∞]→[0,+∞)是关于第二个变量的单调非减连续函数;
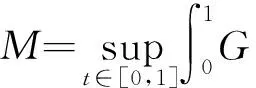
2 主要结论
定理1 假设条件(H1)、(H2)成立,则边值问题(式(1))存在唯一的且是严格单调递增的正解u(t)。
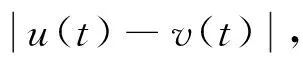
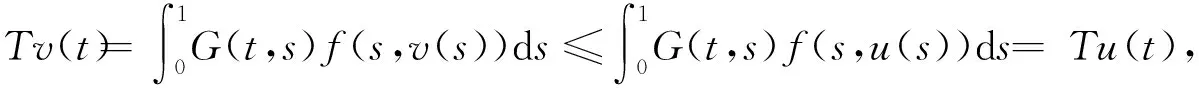
另一方面,由假设条件(H2)和对任意的v≤u,有
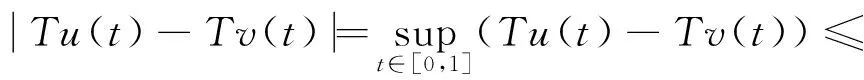
因为函数h(x)=ln(x+1)非减,从而可知
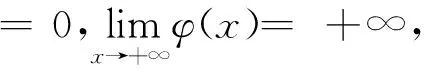
由引理1可知,算子T至少存在一个不动点,该不动点即为边值问题(式(1))的解。因此,边值问题(式(1))至少有一个非负解。又因为(K,≤)满足引理2的条件,所以由引理2可知边值问题(式(1))的解是唯一的。由算子T的定义以及假设条件(H1)易知该解是严格递增的。
[1]GREGUS M.Third order linear differential equations [M].Boston:D Reidel Pub Co,1987.
[2]CABADA A.The method of lower and upper solutions for second,third,fourth,and higher order boundary value problems[J].J Math Anal Appl,1994,185(2):302-320.
[3]GROSSINHO M R,MINHOS F M.Existence result for some third order separated boundary value problems [J].Nonlinear Anal,2001,47:2407-2418.
[4]CABADA A,HEIKKILA S.Extremality and comparison results for discontinuous implicit third order functional initial-boundary value problems [J].J Math Anal Appl,2001,255:195-212.
[5]LIU Z Q,SHEOK J U,KANG S M.Positive solutions of a singular nonlinear third order two-point boundary value problem [J].J Math Anal Appl,2007,326:589-601.
[6]LI S H.Positive solutionsof nonlinear singular third-order two-point boundary value problem [J].J Math Anal Appl,2006,323(1):413-425.
[7]刘瑞宽.一类奇异三阶两点边值问题正解的存在性[J].四川师范大学学报(自然科学版),2014,37(4):482-486
[8]HARJANI J,SADARANGANI K.Fixed point theorems for weakly contractive mappings in partially ordered sets [J].Nonlinear Anal,2009,71(7/8):3403-3410.
[9]NIETO J J,RODRIGUEZ-LOPEZ R.Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations [J].Order,2005,22(3):223-239.
责任编辑:陈 亮
Existence and Uniqueness of Positive Solution for the Third-Order Two-Point Boundary Value Problem
ZHUANG Guohua,WU Chen
(Branch of Nanjing,Jiangsu Union Technical Institute,Nanjing 210019)
10.3969/j.issn.1671- 0436.2015.06.014
2015-11-17
庄国华(1981— ),男,硕士,讲师。
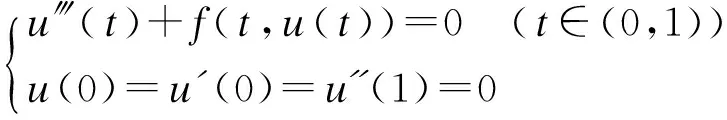
O175.14
A
1671- 0436(2015)06- 0064- 03
