四边固支的双模量矩形板的弯曲计算
2015-06-27张鹏范存新
张鹏,范存新
(江苏省结构工程重点实验室(苏州科技学院),江苏苏州215011)
四边固支的双模量矩形板的弯曲计算
张鹏,范存新
(江苏省结构工程重点实验室(苏州科技学院),江苏苏州215011)
运用弹性力学的相关知识计算出双模量矩形板在外荷载作用下的中性面的具体位置;然后用康托洛维奇法和伽辽金法计算四边固支的双模量矩形板的弯曲;最后列举算例,将计算所得数据与用ANSYS有限元分析软件计算的结果相比较。得出结论:文中所得关于四边固支的双模量的矩形板的弯曲计算公式精度较高;当材料拉压模量差异较大时,在计算中不能忽略双模量的影响。
双模量;四边固支;康托洛维奇法;伽辽金法
Abstract:This paper worked out the position of the neutral plane of bimodulous rectangular plate under the uniform load by applying elastic mechanics theory.The paper deduced the formula for the bending calculation of the bimodulous rectangular plate with four edges clamped by the Kantorovich and Galerkin method.In conclusion,the paper enumerated an example and compared the calculated result based on the deduced formula with the result based on the finite element software.It concluded that the formula for bending calculation of bimodulous rectangular thin plate with four edges clamped has high accuracy.When there is a great difference between tension and compression of the material,the effect of double modulus cannot be neglected.
Key words:bimodulous;four edges clamped;Kantorovich;Galerkin
0 引言
大量研究发现,很多材料具有拉压弹性模量不同的性质,如混凝土、石墨、玻璃、陶瓷等。近几年发展起来的一些复合材料,这种拉压弹性模量不同的性质表现得更为显著。如果计算时忽略这类材料的双模量特性,继续采用等模量的弹性理论解决工程问题,会引起较大误差,给实际工程留下安全隐患,因此,对用这类材料制造的结构和构件采用双模量进行计算分析显得较为重要[1-4]。
对双模量弹性理论课题,很多学者进行了研究,文献[5]研究了双模量的简支梁,文献[6]研究了双模量的连续梁,文献[7]研究了双模量的弯压柱,均得出了双模量特性对构件计算有较大影响的结论。对于双模量矩形板的弯曲计算研究,文献[8]提出了康托洛维奇和伽辽金联合法。此方法是在板的一个方向上假设一个梁函数,通过康托洛维奇法得到四阶微分方程,同时,在板的另一个方向上假设一个未知函数,将未知函数代入四阶微分方程,再通过伽辽金法求得未知函数,得到该矩形板的弯曲挠度公式。该文作者分别研究了三边简支、四边简支2种边界条件下的计算分析,但对于四边固支边界条件的双模量矩形板弯曲计算没有研究探讨。本文运用康托洛维奇和伽辽金联合法对该问题进行研究计算,并对用有限元分析软件ANSYS得出的计算结果进行比较和验证,进一步完善运用康托洛维奇和伽辽金联合法对双模量矩形板的弯曲计算的研究。
1 双模量矩形板的中性面位置
当双模量矩形板发生纯弯曲时,根据内力满足的关系计算出中性面的具体位置。假定双模量的矩形板在变形前后一直满足直法线假定,根据弹性力学的理论可以得到双模量的矩形板在发生纯弯曲时的应力,再根据弹性力学理论可知板的横截面满足平衡关系,计算可得中性面的位置:
(1)
式中:E1、μ1分别为受拉时的弹性模量和泊松比;E2、μ2分别为受压时的弹性模量和泊松比;h为板厚。
2 四边固支的双模量矩形板的弯曲挠度计算
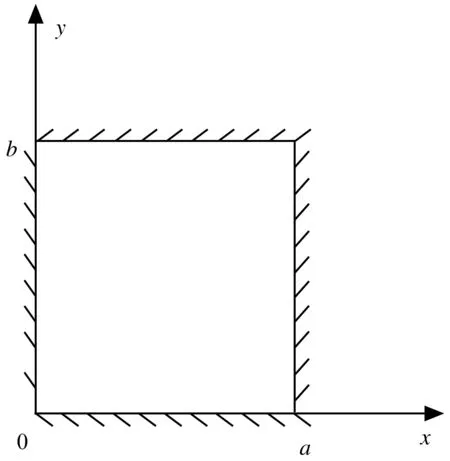
图1 双模量矩形板
对于图1所示双模量矩形板,根据弹性力学理论可知该板由于弯矩引起的变形势能是
(2)
式中:Mx、My分别为双模量矩形板的横截面上绕x轴、y轴的弯矩;Mxy为双模量矩形板的横截面上绕xy面上的扭矩。
在均布荷载作用下,双模量矩形板的势能是
(3)
假设双模量矩形板的挠度函数式是
ω(x,y)=u(x)υ(y)
(4)
式中:υ(y)假定是已知梁函数;u(x)假定是未知梁函数。
根据式(2)、(3)可得双模量矩形板的总势能表达式是
U=U0+U1
(5)
对U进行一阶变分,并利用变分符号和微分符号的可交换性进行分步积分,然后令δU=0,再利用Galerkin原理计算可得
(6)
对于受均布荷载作用的四边固定的双模量矩形板,可以假设:
(7)
由式(7)可计算得:
(8)
分别代入式(9)
(9)

(10)
由式(9)、(10)可得
(11)
将式(11)代入式(6)可得
(12)
整理计算可得
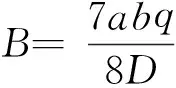
(13)
因此,可得双模量矩形板的挠度函数式
(14)
当a=b,E1=E2,μ1=μ2时,通过式(14)可求得各向同性材料的四边固支板的挠度函数
(15)
利用式(15)计算四边固支正方形板中心的挠度为ω(a/2,a/2)=0.001 30qa4/D,用康托洛维奇法[9]计算为ω(a/2,a/2)=0.001 26qa4/D,两者误差为3%,说明计算结果是可靠的。
3 算例和讨论
为了检验推导所得的双模量矩形板的挠度函数式的准确性,分别计算2种材料的四边固支矩形板受均布荷载1 MPa作用下的挠度。2种材料的力学参数见表1。

表1 材料和板的参数
1)当a=b时,
分别计算材料1、材料2组成的板在(x=a/2,y=b/2)、(x=a/4,y=b/4)、(x=a/2,y=b/4)位置处的挠度值,并用有限元软件ANSYS模拟计算,得到的误差值见表2。
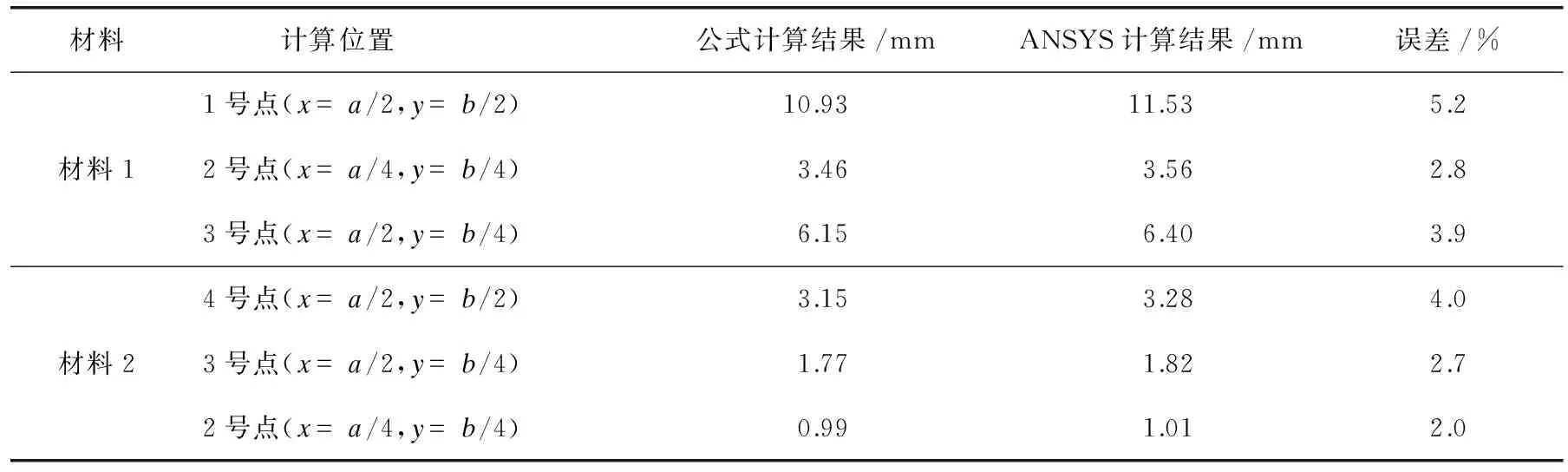
表2 公式计算结果和ANSYS计算结果比较(a=b)
2)当a=1.1b时,
分别计算材料1、材料2组成的板在(x=a/2,y=b/2)、(x=a/4,y=b/4)、(x=a/2,y=b/4)位置处的挠度值,并用有限元软件ANSYS模拟计算,得到的误差值见表3。

表3 公式计算结果和ANSYS计算结果比较(a=1.1b)
由表2、表3可知,采用本文公式计算的结果和ANSYS计算结果很接近,验证了该公式的可靠性。通过比较两表数据结果可以发现,有限元软件计算结果比本文公式计算结果偏大,主要是由于有限元软件在计算挠度时还考虑了板的剪切变形,而本文计算公式未考虑剪切变形。另外,由表2、表3和图2、图3的数据可以发现:在该板挠度越小的位置,计算公式的计算精度越高,这与本文中的直法线假定有一定关系,因为挠度越小该假定越可以得到满足;四边固支的双模量矩形板受均布荷载时,越到板中间位置挠度越大,因此该板和普通板一样,其中间位置的挠度在受均布荷载下时值得注意,不过由于该板的约束比四边简支和三边简支时约束强,因此前者的挠度比后者小;随着该板长与宽的比值增大,板的挠度减小,说明该板的刚度增加了。
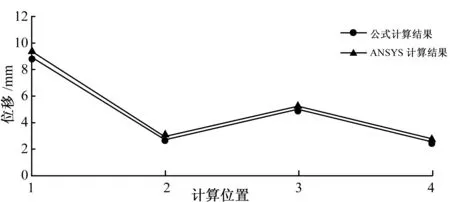
图2 材料1公式计算和ANSYS计算比较(a=b)
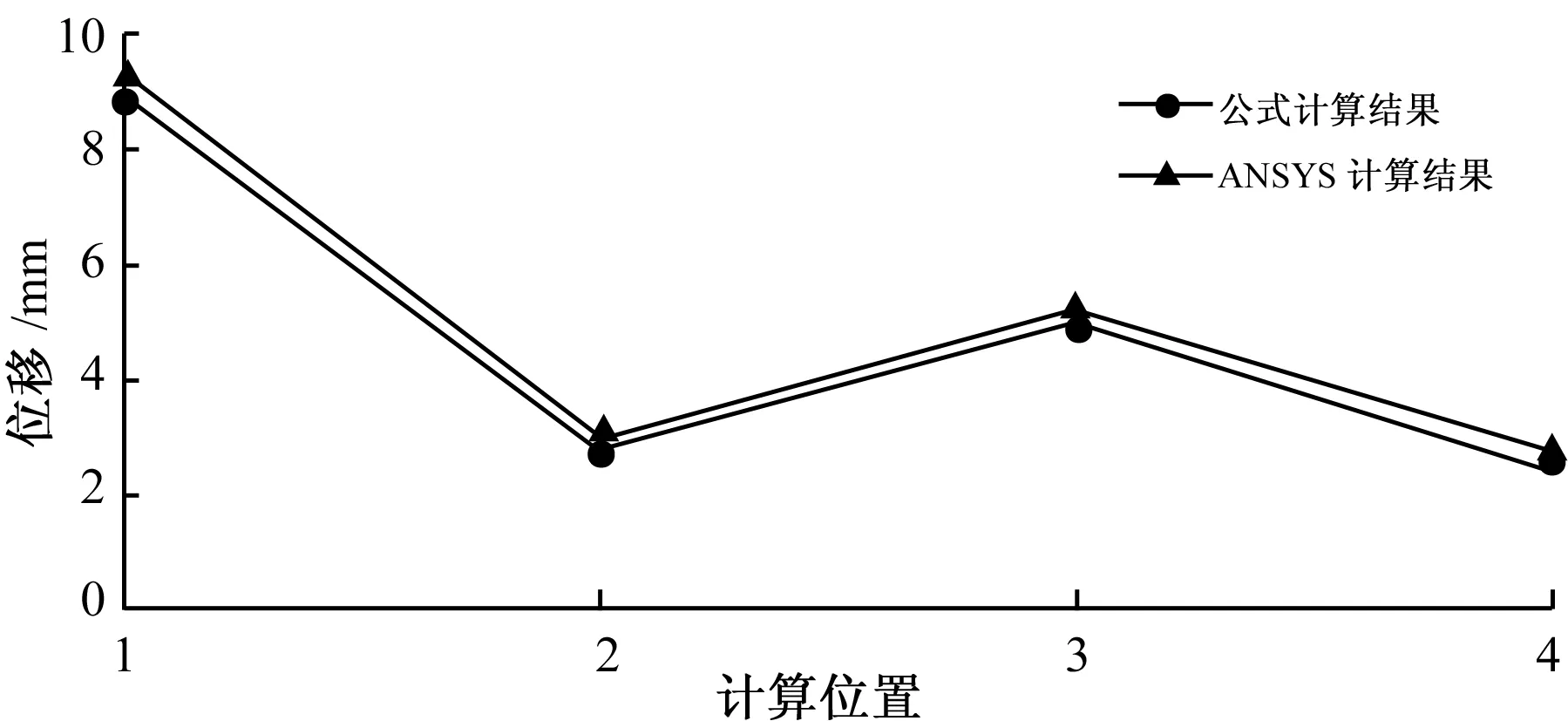
图3材料1公式计算和ANSYS计算比较(a=1.1b)
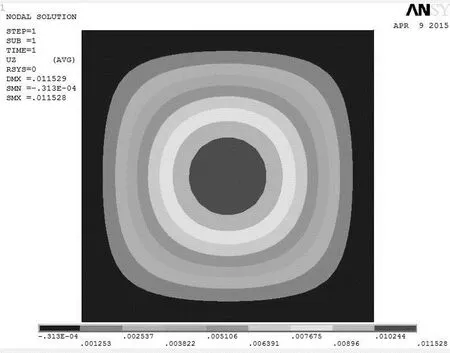
图4 平面外的位移云图
若忽略双模量的影响,假设a=b,按公式ω(a/2,a/2)=0.001 26qa4/D,取表4中材料3计算,得板中心挠度为6.98 mm。若考虑双模量影响,采用材料1的参数,由ANSYS结果(图4)得板中心挠度为11.53 mm,误差约为40%。显然,当拉压模量差异很大时,在实际的计算中不能忽略双模量的影响。
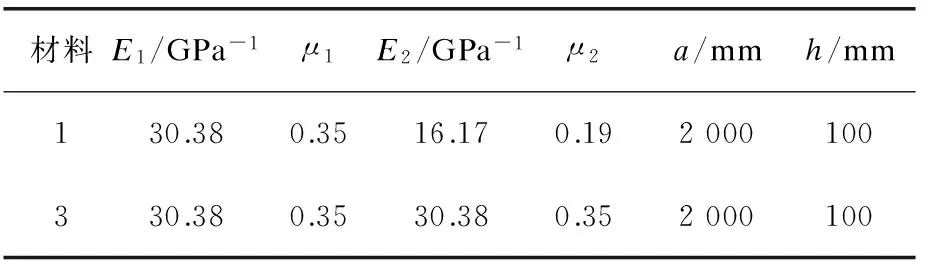
表4 材料和板的参数
4 结论
1)ANSYS计算结果和文中公式的计算结果非常接近,说明本文的计算结果具有可靠性,计算该类双模量板时可以采用该计算公式;当拉压模量差异很大时,如果按照相同的弹性模量计算,计算误差会很大,因此在实际的计算中遇到这类材料不能忽略双模量对内力位移的影响。
2)在相同材料的情况下,四边固支的双模量矩形板的挠度越小,该公式计算的精度相对越高;随着该板长与宽的比值增大,该类型的板的刚度在增加。
[1]罗战友,夏建中,龚晓南.不同拉压模量及软化特性材料的柱形孔扩张问题的统一解[J].工程力学,2008,25(9):79-84.
[2]赵慧玲,叶志明.拉压不同模量弹性问题[J].上海大学学报(自然科学版),2014,20(5):550-558.
[3]何晓婷,陈山林.不同模量弹性力学问题研究进展[J].重庆建筑大学学报,2006,27(6):136-141.
[4]蔡来生,俞焕然.拉压模量不同弹性物质的本构[J].西安科技大学学报,2009,29(1):17-21.
[5]王蔚佳,邹文成,陈强.基于双模量理论的均布载荷下简支梁的解析解及数值分析[J].工业建筑,2013,43(6):56-59,89.
[6]姚文娟,叶志明.不同拉压模量连续梁的解析解[J].力学季刊,2011,32(1):68-73.
[7]姚文娟,蒋小芳.拉压不同模量弯压柱的有限元数值解[J].南昌大学学报(工科版),2005,27(1):40-45
[8]吴晓.用 Kantorovich及Galerkin 联合法研究双模量板的弯曲[J].西安建筑科技大学学报(自然科学版),2012,44(4):457-462.
[9]王磊.平行四边形板弯曲问题的康托洛维奇法[J].湖南大学学报(自然科学版),1983(4):36-46.
责任编辑:唐海燕
Bending Calculation of Bimodulous Rectangular Plate with Four Edges Clamped
ZHANG Peng,FAN Cunxin
(Key Laboratory of Structure Engineering in Jiangsu Province,Suzhou University of Science and Technology,Suzhou 215011)
10.3969/j.issn.1671- 0436.2015.06.001
2015-10-19
张鹏(1990— ),男,硕士研究生。
TU313.1
A
1671- 0436(2015)06- 0001- 06
