我国区域研发投入产出有效性研究

徐 磊，周 帆

(四川外国语大学 a.国别经济与国际商务研究中心;b.综合档案室，重庆 400031)

一、引言

研究与开发(Research＆ Development，R＆D)活动是一个国家或地区科技进步及经济发展的主要推动力，因此各国及地区都试图通过加大R＆D投入力度来促进科技进步及经济发展。近年来，我国提出建设创新型国家的奋斗目标，研发投入呈现迅猛增长趋势，已从1990年的125.43亿元增长到2012年的10298.41亿元;研发人员数量从1990年的61.71万人增长到2012年的461.7万人;R＆D支出占 GDP的比例由2000年的0.9%提高到2012年的1.98%①数据来源于相关年度的《中国科技统计数据》。，并且首次超过欧盟28国1.96%的总体比例。然而，在充分肯定我国研发投入非凡成就的同时，更应清楚地意识到与发达国家之间的巨大差距。世界银行数据显示，2012年美国、德国、日本及韩国的研发投入强度分别为 2.79%、2.92%、3.34%及4.36%，远远高于我国的研发投入强度，甚至高于《国家中长期科技发展规划纲要》设定的到2020年达到2.5%的目标。在当前我国研发投入依然有限的情况下，如何利用较少的R＆D投入实现最大的经济效益和社会效益就显得尤为重要。这不仅是研发投入产出问题，更是科技资源的区域配置问题。由于我国社会经济发展存在较大区域差异，所以，从区域层面考察我国R＆D效率问题更为合理。［1］因此，从区域层面实证测度我国研发投入产出效率，对于客观评估我国各地区研发投入的相对有效性，实现我国科技资源区域最优配置，以提高整体研发效率并最终促进我国经济增长具有重要的现实及理论意义。

二、文献综述

效率一般可以采用参数法及非参数法两种方法进行测度，随机前沿分析法(SFA)属于参数法。近年来，国内外基于SFA方法的技术效率实证研究比较深入。何枫等(2004)较早地引入SFA模型，对我国改革开放以来20年间的技术效率变迁进行测算，结果表明，我国平均技术效率水平稳步上升，但呈现东部沿海地区＞中部地区＞西部地区的格局。［2］安良同等(2006)基于调查问卷，指出我国小公司、中型公司、大公司的R＆D强度趋势存在着明确的倾斜的V型结构关系。［3］李平等(2007)的研究结果表明，中国自主创新能力的提升主要依靠国内自主R＆D投入，人力资本和知识产权保护对R＆D投入产出效率影响存在差异。［4］陈金丹(2008)用SFA方法测算了我国31个省份的R＆D效率，发现省域R＆D效率与经济发展水平并无必然的正向关系。［5］黄凌云和鲍怡(2009)借助SFA方法，研究表明我国制造业的技术效率逐年提高，FDI和国有程度高低对制造业技术效率分别存在正的和负的影响。［6］刁丽琳等(2011)运用SFA方法对全国28个省份技术效率及其科技环境影响因素进行估计，结果表明，中国技术效率东部和中西部两级分化严重，全国各地区的技术效率随时间推移呈下降趋势，政府科技投入与效率损失负相关。［7］朱承亮等(2012)采用SFA方法研究发现，中国R＆D效率整体较低，有较大的创新潜力;中国R＆D效率区域差异明显且呈现发散趋势;效率损失存在于专利成果市场化过程中。［8］

另一种是非参数法，数据包络分析法(DEA)是常见的非参数估计法，DEA方法同样广泛应用于有关R＆D效率的研究中。刘顺忠和官建成(2002)运用DEA方法分析我国各地区创新系统的特点，并将我国各地区的区域创新系统进行分类。［9］Revilla等(2003)则用 DEA 方法评价了公共与私立研究机构的合作R＆D绩效。［10］梁莱歆等(2006)的研究表明，R＆D效率与企业规模存在一定联系，并指出采用DEA方法进行企业效率评价时，评价指标的选取直接决定着结果解释的合理程度。［11］龙勇和李薇(2008)将DEA方法引入到多时段生产效率变化指数模型，结果表明，与竞争对手合作实施R＆D能够在较大程度上提高组织的总体研发效率，促进产业技术水平升级。［12］Sueyoshi等(2009)应用 DEA － DA(DEA判别分析)模型对日本机械工业和电力设备工业的 R＆D支出效果进行评价。［13］张海洋(2010)把DEA模型引入全要素R＆D效率估算框架，对1999～2007年省级大中型工业全要素R＆D效率及其组成全要素R＆D资本效率和全要素R＆D人员效率的变化特点和影响因素进行了分析。［14］王晓红等(2010)通过构建 DEA 模型，实证分析表明，“十五”期间我国各省份的R＆D效率整体处在下行区间，且省份间的差异先扩大再缩小，整体差异较为显著。［15］进一步地，吴和成等(2010)指出，我国“十五”期间有60%以上的制造行业R＆D投入资源未能得到有效利用，R＆D效率呈现出波动变化。［16］胡象明和李心萌(2012)指出，我国不同产业领域的R＆D活动投入产出效率不同，并且区分了不同产业的技术效率和规模效率。［17］韩东林和张琼芝(2012)基于DEA模型，评价了2009年我国省域规模以上工业企业的R＆D效率，结果表明，2009年各省份规模以上工业企业的R＆D效率普遍不高，大多数省份存在 R＆D投入冗余和不足问题。［18］

以上文献分别采用SFA法及DEA法，从不同角度及层面对R＆D效率进行了实证研究，为相关研究奠定了坚实的基础。然而，由于DEA法及SFA法各自具有自身的特点及适用的领域，鲜有研究同时采用两种方法对R＆D效率进行测度。实际上，这两种方法已经开始被用到同一领域进行其他效率的测度，实现非参数方法和参数方法的优势互补。有鉴于此，本文尝试同时使用SFA法及DEA法对中国区域R＆D效率进行测度，并对两种方法的测度结果进行对比分析，考察这两种方法在我国区域R＆D效率测算中的实用性，期望得到R＆D效率变化的基本规律，反映省际R＆D技术效率的真实水平及区域差异，为政府决策提供实证参考。

三、理论框架与数据说明

(一)模型设定

1.SFA 模型

借鉴 Battese 和 Coelli(1992)［19］模型的思想，结合柯布－道格拉斯生产函数，利用SFA法对我国各地区研发效率进行测度，模型的具体形式为：

其中，Yit为i省份t时期的R＆D产出，用该省份第t+1年的专利申请授权量表示，即假设我国研发投入产出的滞后期为1年;Kit为i省份t时期研发资本的投入，用该省份第t年R＆D经费支出表示;Lit为i省份t时期研发人员的投入，用该省份第t年研发人员的全时当量表示;TEit为 i省份 t时期的研发效率;β0为截距项，β1、β2、η和γ为有待估计的参数;Vit－Uit为误差项，其中Vit为随机误差项，Vit∈iid并服从N(0，)分布，Uit为无效率部分，Uit≥0，反映那些在 t时期仅仅影响i 省份的随机因素，Uit∈iid服从在零处截断、均值为u、方差为的半正态分布，同时Vit与Uit相互独立;第三个式子定量描述了时间因素对Uit的影响。γ是Vit中无效率所占的比例，借此可以判断模型设定的合理性。如果γ=0，表明实际研发效率与可能的最优研发效率的差距主要来自不可控制的白噪音误差，即说明样本中各省份的研发投入都位于最优产出水平上，没有必要使用SFA 方法，而直接用OLS方法即可。

2.DEA模型

Charnes等(1977)提出了DEA的原始模型C2R，［20］该模型假定在规模报酬不变的情况下评价各决策单元(Decision Making Units，DMU)的相对有效性，不能很好地区分出有效(即效率值为1)DMU之间的差异，因此本文采用超效率DEA模型，［21］对我国各省份的研发效率进行测度，具体模型如下：

其中，θ0为所评价的第 j0个决策单元(DMU)的效率值，xjoi为其投入向量，yj0为其产出向量;xji表示第j个决策单位DMU中第i个投入向量，实际上本文只有研究资本及研发人员两种投入指标，yj表示第j个决策单位DMU的产出向量，λj为新构造一个有效决策单元(DMU)组合中第 j个决策单元(DMU)的权重向量，和分别为按该权重计算的决策单元(DMU)组合中的投入指标和产出指标向量。

(二)数据来源及处理

SFA及DEA两种测度方法中使用的所有数据来源于历年的《中国科技统计年鉴》、《中国统计年鉴》、《中国科技统计数据》、中国科学技术部网站及国家知识产权局网站，其中各省份每年的R＆D经费支出按照 GDP平减指数折算为2004年的基准价格。

四、实证结果分析

(一)SFA模型估计结果分析

运用Frontier 4.1软件对SFA模型进行估计，结果见表1和表2。从表1可以看出：(1)γ的值为正(0.841)，且LR单边检测误差值大于显著性概率为1%的卡方临界值，γ=0的假设被拒绝，存在技术非效率项u，这说明我国R＆D活动存在着效率损失，因此使用SFA模型是适宜的。(2)超对数柯布－道格拉斯生产函数自变量系数 β1=0.307，β2=0.683，劳动的产出弹性大于资本的产出弹性。实际上，R＆D投入是资本和人员投入的结合，相比于资本投入，R＆D人员劳动稍显重要，这也意味着劳动者素质的提高对于推动R＆D效率具有更重要的实际意义。(3)η=0.038，这表明各省份的无效率将随着时间的推移而加速下降，即各地区的研发效率呈上升趋势。

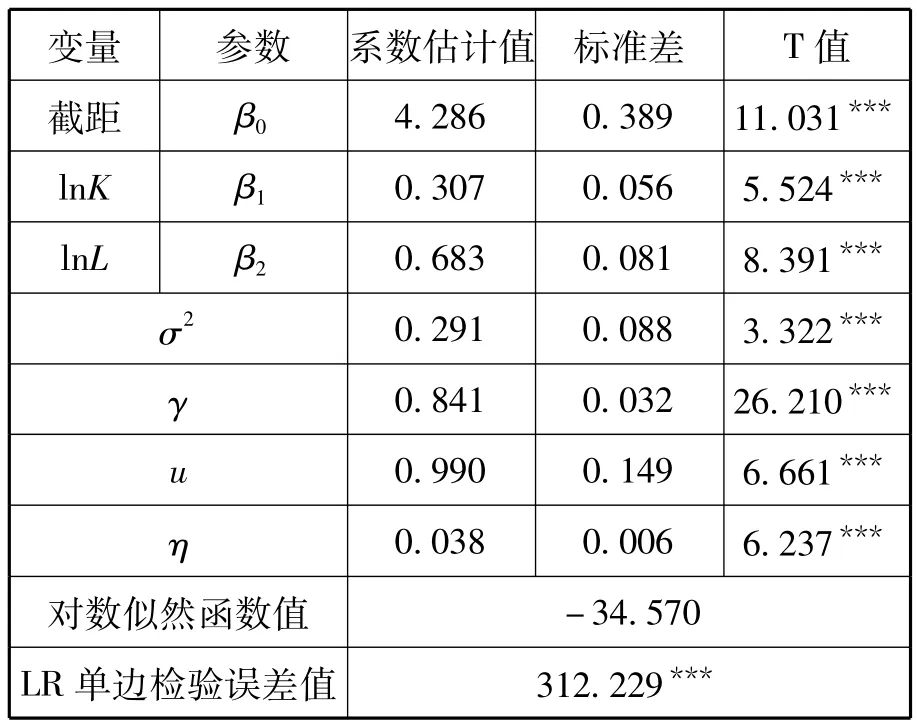
表1 SFA模型参数估计值

从表2可以看出，各省份技术效率逐年提高，效率均值由2004年的0.332逐年上升到2012年的0.417。31 个省份中，上海、江苏、浙江、福建、山东、广东、海南、重庆及新疆等省份的效率均值分别为 0.511、0.397、0.904、0.521、0.462、0.853、0.671、0.495 及 0.547，均高于平均技术效率值0.377;而其他省份均低于这个均值。在4个直辖市中，只有上海和重庆高于平均技术效率值，其中北京最低，均值只有0.238。就经济区域结构而言，东南沿海地区中，山东、江苏、上海、浙江、福建、广东及海南等省份技术效率值均高于均值;中部地区技术效率普遍低于均值;西部地区有重庆和新疆技术效率高于均值，这与我国多年来在经济科技基础相对薄弱的西部地区推行大开发战略，技术“后发优势”有所显现所致，西部地区超过了中部地区，呈东部＞西部＞中部的格局，这说明中部地区R＆D效率提高相对较慢。

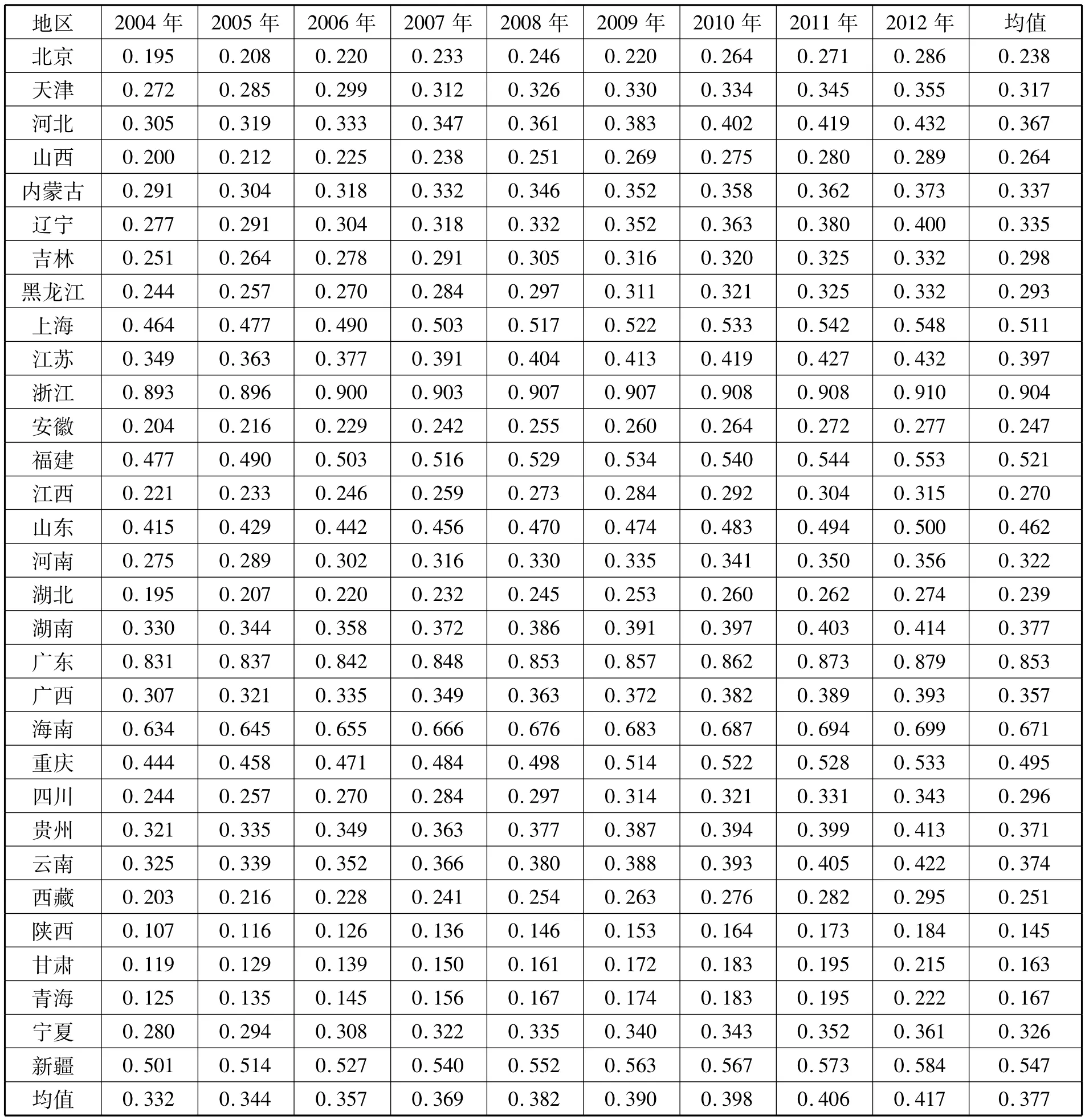
表2 省际2004～2012年R＆D活动的效率统计(SFA模型)

(二)DEA模型估计结果分析

用DEAP 2.1软件对DEA模型进行估计，结果如表3所示。各省份的技术效率并不是逐年提高的，而是呈现波动上升趋势。2004～2012年效率均值分别是 0.471、0.461、0.46、0.494、0.466、0.442、0.463、0.493 和 0.515。在 31 个省份中，上海、江苏、浙江、福建、山东、河南、广东、广西、海南、重庆、贵州、西藏、新疆等省份的效率均值分别为 0.622、0.576、0.978、0.487、0.521、0.484、0.887、0.554、0.679、0.670、0.664、0.659 和 0.799，均高于平均技术效率值0.474;而其他省份均低于这个均值。在4个直辖市中，只有上海和重庆高于平均技术效率值，其中北京最低，均值只有0.241。就经济区域结构而言，东南沿海地区中，山东、江苏、上海、浙江、福建、广东、海南等省份技术效率值均高于均值;中部地区普遍低于均值，只有河南省的技术效率高于均值，这说明中部地区R＆D效率提高相对较慢;西部地区有重庆、贵州、西藏和新疆技术效率高于均值，西部地区的表现超过了中部地区，也呈现东部＞西部＞中部的格局。

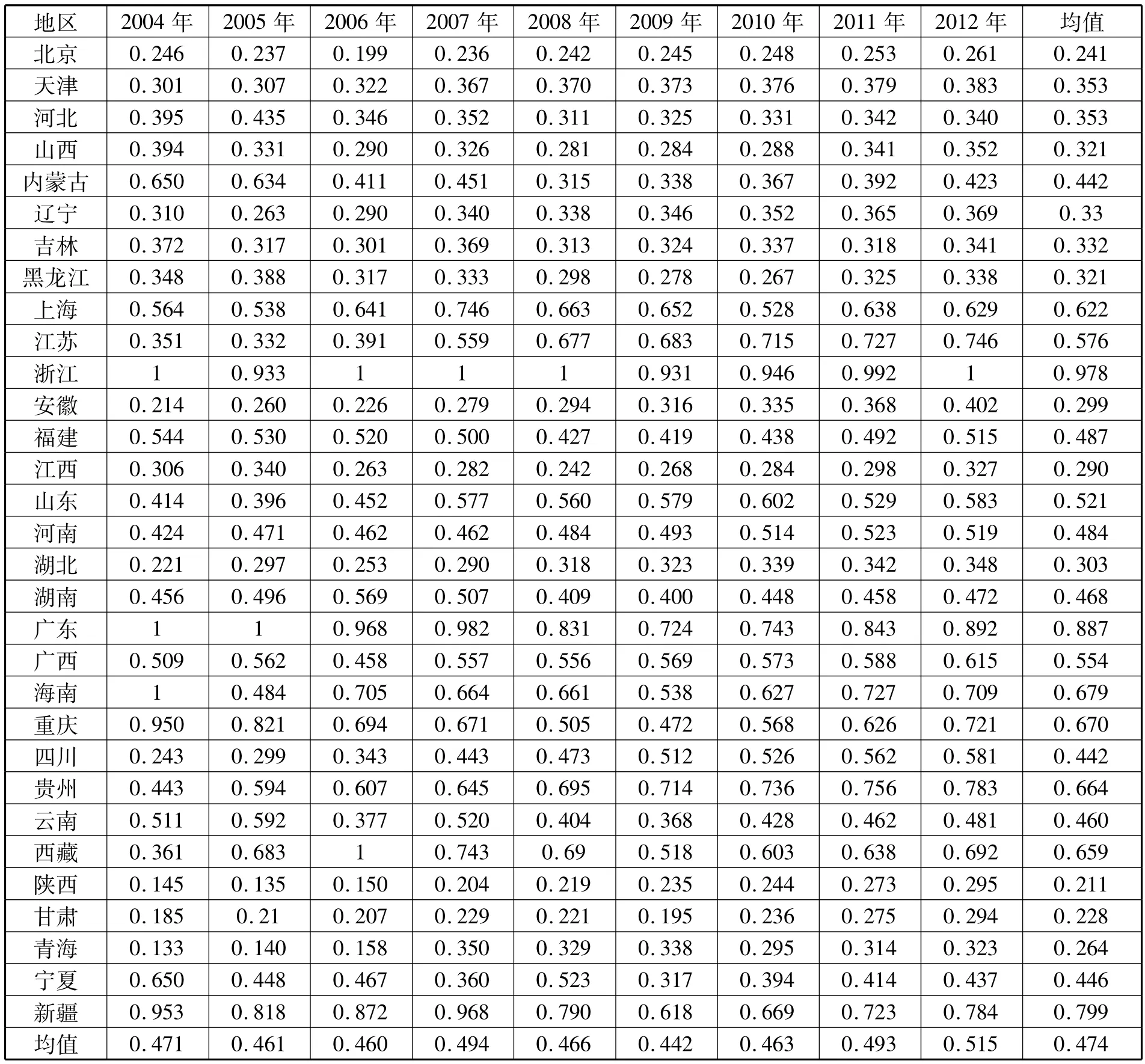
表3 省际2004～2012年R＆D活动的效率统计(DEA模型)

(三)SFA方法和DEA方法的比较分析

通过比较两种方法的测度结果可以发现：(1)两种方法估计出来的结果总体上具有方向一致性。但使用SFA方法，各地区的研发效率随时间呈稳定上升趋势，而使用DEA方法得出的效率结果出现了波动，效率值排名也出现一定的差异。(2)两种方法得出的结果接近，DEA方法比SFA方法得出的结果要略大。(3)从结果来看，除上海、浙江、广东、江苏、福建等经济较发达省份外，其他地区的研发效率都比较低，表明我国研发效率还有很大的提升空间(与1相差甚远);使用两种方法测度的技术效率值总体上都呈现出东部＞西部＞中部的格局。以上结果充分证明这两种方法都是我国区域研发效率的有效测算方法。尽管如此，虽然本文使用的数据相同，但两种方法的测算结果确实存在一定差异，究其可能的原因有多种。孙巍(2000)认为，差异主要在于这两种方法在模型、前提假设和统计方法上的不同，［23］具体而言，SFA模型因设定了具体的函数形式可能带来局限性，而DEA模型避免了模型设定的误差。［24］除了模型的不同，程慧平(2013)指出，SFA考虑了影响技术效率的随机因素，而DEA侧重分析了不同省份的相对技术效率水平，从而引起结果不同。［25］另外，张宇青等(2013)还指出，SFA类似于回归分析，能够在效率测算的同时分析出各大变量在整体上如何影响产出水平。［26］而针对本文的情况，效率测算结果的差异，可能是因为在实证中，SFA使用面板数据测算得出的是各地区各年度的研发效率，而DEA使用的是截面数据，在对每年各省份数据经过一次计算之后，得出的是各省份在本年度的研发效率。

(四)SFA方法和DEA方法的OLS估计

为了进一步分析两种方法所得效率值之间的关系，将使用SFA方法测算的技术效率值作为被解释变量，DEA方法测算的技术效率值作为解释量，对两者进行普通最小二乘法回归分析。结果如表4所示。

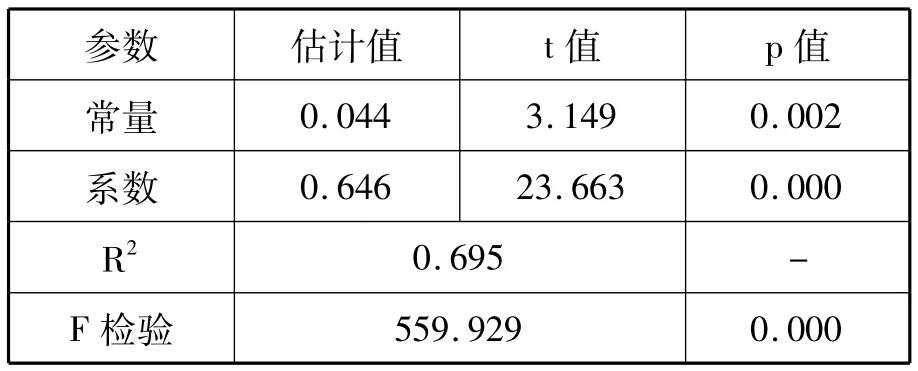
表4 SFA方法和DEA方法的OLS估计(d.f=246)

由表4可以看出，方程判定系数 R2为0.695;F检验值为 559.929;方程截距项为0.044，显著性水平为 0.002;自变量系数为0.646，显著性水平为0。这充分说明本文采用的两种方法计算出来的效率值之间存在着很强的正相关性。令TESFA和TEDEA分别为使用SFA方法和DEA方法测算的效率值，则拟合的回归方程为：

五、结论

以2004～2012年间全国31个省份的面板数据为基础，同时利用SFA及DEA两种效率测度方法实证分析我国各区域研发投入产出的有效性。得出以下结论：(1)使用SFA方法，我国各地区的研发效率随时间呈稳定上升趋势，R＆D活动存在着效率损失，在超对数柯布－道格拉斯生产函数中，劳动的产出弹性大于资本的产出弹性，意味着劳动者素质的提高对于推动R＆D效率具有重要的实际意义;而使用DEA方法得出的效率结果呈现出波动上升趋势。(2)两种方法测度出来的效率值结果总体上具有方向一致性，但效率排名具有一定差异;DEA方法比SFA方法得出的结果略大，并且两种方法所得技术效率值之间存在着正相关关系。(3)技术效率呈现区域不平衡，除上海、浙江、广东、江苏及福建等经济较发达省份外，其他地区的研发效率都比较低，表明我国研发效率还有很大的提升空间(与1相差甚远);使用两种方法测度，技术效率值总体上都呈现出东部＞西部＞中部的格局。

［1］Li X.China's Regional Innovation Capacity in Transition:An Empirical Approach［J］.Research Policy，2009，38(2):338－357.

［2］何枫，陈荣，何炼成.SFA模型及其在我国技术效率测算中的应用［J］.系统工程理论与实践，2004，(5):46－50.

［3］安良同，施浩，Ludovico Alcorta.中国制造业企业R＆D行为模式的观测与实证——基于江苏省制造业企业问卷调查的实证分析［J］.经济研究，2006，(2):21－30.

［4］李平，崔喜君，刘建.中国自主创新中研发资本投入产出绩效分析——兼论人力资本和知识产权保护的影响［J］.中国社会科学，2007，(2):32－42.

［5］陈金丹.基于SFA方法的我国各省市R＆D有效性研究［J］.商业经济，2008，(8):26－27，65.

［6］黄凌云，鲍怡.制度特征、FDI对我国制造业技术效率的影响——基于行业数据的分析［J］.经济学家，2009，(11):22 －29.

［7］刁丽琳，张蓓，马亚男.基于SFA模型的科技环境对区域技术效率的影响研究［J］.科研管理，2011，(4):143－151.

［8］朱承亮，师萍，安立仁.人力资本及其结构与研发创新效率——基于SFA模型的检验［J］.管理工程学报，2012，(4):58－64.

［9］刘顺忠，官建成.区域创新系统创新绩效的评价［J］.中国管理科学，2002，(1):75－78.

［10］Revilla E，Sarkis J，Modrego A.Evaluating Performance of Public－private Research Collaborations:A DEA Analysis［J］.Journal of the Operational Research Society，2003，54(2):165－174.

［11］梁莱歆，张焕凤，袁艺.基于DEA的企业R＆D有效性研究［J］.科研管理，2006，(6):68－73，143.

［12］龙勇，李薇.竞争性战略联盟中合作R＆D效率的DEA分析［J］.科研管理，2008，(4):76－81.

［13］Sueyoshi T，Goto M.Can R＆D Expenditure Avoid Corporate Bankruptcy?Comparison between Japanese Machinery and Electric Equipment Industries Using DEA － discriminant Analysis［J］.European Journal of Operational Research，2009，196(1):289－311.

［14］张海洋.中国省际工业全要素R＆D效率和影响因素:1999－2007［J］.经济学(季刊)，2010，(4):1029－1050.

［15］王晓红，陈浩，孙玮.我国“十五”期间R＆D效率的省域研究［J］.科研管理，2010，(5):185－191.

［16］吴和成，华海岭，杨勇松.制造业R＆D效率测度及对策研究——基于中国17个制造行业的数据［J］.科研管理，2010，(5):45－53.

［17］胡象明，李心萌.基于DEA模型的中国高技术产业大中型工业企业R＆D效率的实证研究［J］.东北师大学报:哲学社会科学版，2012，(3):35－38.

［18］韩东林，张琼芝.我国工业企业R＆D投入产出效率的省际差异——基于第二次全国R＆D资源清查数据［J］.技术经济，2012，(11):31－35.

［19］Battese G.E.，Coelli，T.J.Frontier Production Functions，Technical Efficiency and Panel Data:With Application to Paddy Farmers in India［J］.Journal of Productivity Analysis，1992，(3):153 －169.

［20］Charnes A，Cooper W W，Rhodes E.Measuring the Efficiency of Decision Making Units［J］.European Journal of Operational Research，1977，2(6):429－444.

［21］Andersen P，Petersen N C.A Procedure for Ranking Efficient Units in Data Envelopment Analysis［J］.Management Science，1998，39(10):1261 －1264.

［22］Kodde D A，Palm F C.Wald Criteria for Jointly Testing Equality and Inequality Restrictions［J］.Econometrica，1986，54(5):1243－1248.

［23］孙巍.生产资源配置效率——生产前沿理论及其应用［M］.北京:社会科学文献出版社，2000.

［24］万兴，范金，胡汉辉.江苏制造业TFP增长、技术进步及效率变动分析:基于SFA和DEA方法的比较［J］.系统管理学报，2007，(5):465－471.

［25］程慧平.基于DEA和SFA方法的信息服务业技术效率研究［J］.科学学与科学技术管理，2013，(4):28－34.

［26］张宇青，易中懿，周应恒.我国省际R＆D活动效率评价研究:基于DEA和SFA模型［J］.科学管理研究，2013，(4):90－93.