基于频率特性搜索的伺服系统谐振控制
2015-06-26熊琰李叶松
熊琰,李叶松
(华中科技大学自动化学院,湖北武汉430074)
1 引言
在工业应用中,伺服传动系统一般采用传动杆、齿轮、同步带等机械传动装置来驱动工作台。为了获得伺服系统的最佳转矩传递特性,在设计控制器的过程中,必须考虑这些机械传递部件的特性[1-3]。在连接电机和负载的机械传动装置中,降低伺服系统动态特性的主要因素是机械装置的传动刚度,刚度过小会导致机械谐振频率与伺服系统的速度闭环带宽重叠,系统会出现不稳定,甚至损坏机械传动装置。在轧机、传送带、机械手臂、造纸机等伺服系统的工业应用中,机械谐振已经成为影响系统特性的主要因素之一。
国内外学者提出了多种控制策略来抑制系统的机械谐振。基于状态变量反馈是抑制机械谐振的一种有效的方法[4-5],伺服系统的状态变量通过观测器观测得到,然后利用极点配置的方法设计速度控制器的参数。但是在实际应用中,高带宽的状态观测器会放大伺服系统的测量噪声,而较小的观测器带宽会降低估算的精度。因此,状态观测器较少应用于具有高频谐振的系统中[6]。
通过在线对电机转速反馈和转速给定的差值进行FFT 变换,辨识得到伺服系统的谐振频率,然后设计自适应陷波滤波器是另一种简单有效的方法[7-8]。但是,通过差值的FFT变换只能检测得到系统的谐振频率,并不能检测得到系统在谐振频率处的幅度增益和谐振带宽,所设计的陷波滤波器不能很好地抑制机械谐振。利用正弦信号作为速度环给定,求得谐振频率处的反馈转速和给定转速幅值的比值可以获取系统在谐振频率的幅度增益和带宽[9-10]。但是,在机械谐振频率与略低于速度环穿越频率时,电机振荡的频率高于机械谐振频率,会导致设计的陷波滤波器抑制机械谐振失败[11]。另一方面,一般的陷波滤波器只是在频率响应上减小了谐振频率处的幅度增益,并不能与谐振环节完全相抵消,影响了系统的动态响应特性[12]。
本文首先通过动力学方程对伺服机械谐振系统进行建模,分析了系统机械谐振的频率特性。然后提出了一种通过分割搜索区间的迭代搜索算法,该算法能准确获取伺服机械谐振系统的频率特性。在搜索完成后,利用系统的频率特性设计和优化陷波滤波器的参数,从而抑制伺服系统的机械谐振。仿真和实验证明,所提出的搜索算法方法能够准确获取伺服机械谐振系统的频率特性;设计的陷波滤波器不仅较好地抑制了系统的机械谐振,而且改善了系统的动态响应特性。
2 伺服系统机械谐振模型的建立与分析
典型的伺服系统由控制器、电机、机械传动装置和负载组成。其中,控制器控制电机输出转矩,输出的转矩通过齿轮,同步带,丝杠等机械传动装置进行有效传递,从而驱动负载运动。
建立图1所示的简化物理模型对伺服机械谐振系统进行描述。图1 中,n 为等效机械传动机构的个数;ωm和θm分别表示电机转速和电机位置;ωn和θn分别是负载的转速和位置;Te是电机输出转矩,Tsn表示传动机构的转矩;Jm和Jn分别是电机侧等效转动惯量和等效负载转动惯量;Ksn和Kwn分别表示等效传动机构的刚度和粘滞阻尼系数。通常,伺服机械谐振系统的等效机械传动机构的个数n为1或者2,谐振系统也分别被称为二质量系统和三质量系统[13]。

图1 伺服谐振系统的简化物理模型Fig.1 The simplified physic model of servo resonant system
为了方便分析,忽略电机受到的摩擦转矩、传动机构的间隙和传动机构的粘滞阻尼,建立动力学方程对伺服机械谐振系统进行数学描述:
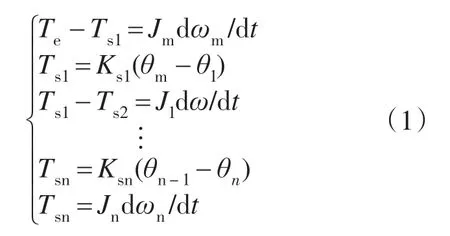
利用上述方程可以推导出伺服机械谐振系统的传递函数:
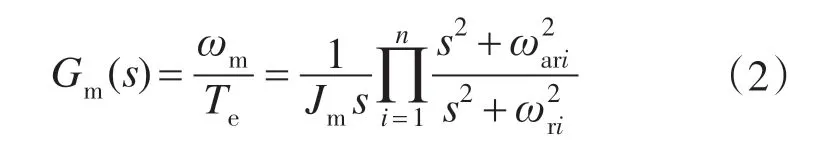
引起伺服系统谐振的机械谐振环节的传递函数为

以二质量系统为例,其传递函数的参数与机械参数有如下关系:

类似的,三质量系统的传递函数的参数与机械参数的关系为
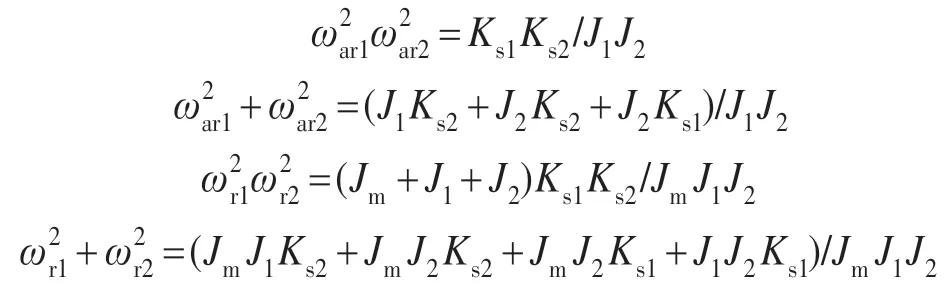
对式(2)进行频域分析,可以获取伺服机械谐振系统的频率特性,图2 给出了二质量系统和三质量系统的幅频特性。可以看出,二质量系统具有一对谐振频率和反谐振频率;三质量系统具有两对谐振频率和反谐振频率。在反谐振频率处,系统幅度增益较小;在谐振频率处,系统幅度增益较大。因此,当机械谐振频率小于速度环的截止频率时,谐振频率点处的增益会导致电机转速产生机械振荡。
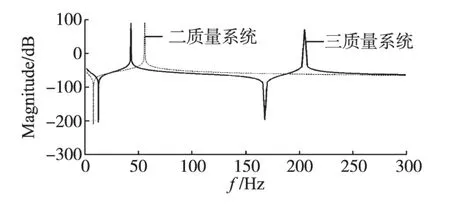
图2 二质量系统和三质量系统的幅频特性Fig.2 The magnitude-frequency characteristic of threemass system and two-mass system
为了抑制伺服系统的机械振荡,在伺服控制器中加入低通滤波器、陷波滤波器等方式都是比较有效的手段,要设计这些滤波器,需要准确检测出系统的频率特性。
3 系统谐振频率特性的搜索
在实际伺服系统中,速度控制器存在输出限幅,因此,在忽略掉控制器积分项在高频下的作用时,速度环控制器的描述函数可以用下式表示:

式中:kp为速度环控制器的增益;d为速度环控制器线性区域宽度。
由式(4)可知,在2A≥d时,-∞<-1/N(A)≤-1/kp。设伺服系统电流环等效传递函数为Gc(s),当Gc(s)Gm(s)的奈奎斯特曲线与-1/N(A)存在交点时,伺服系统会以该交点对应的频率产生持续的振荡。Gc(s)Gm(s)的伯德图如图3 所示,在图3 中,系统穿越-180°的频率即为奈奎斯特曲线与-1/N(A)交点处的频率,由于该频率大于谐振频率,因此对转速进行FFT变换检测得到的频率并不是实际的谐振频率。

图3 机械环节和电流环的伯德图Fig.3 The bode diagram of mechanical part and current loop
为了避免速度环穿越频率的影响,本文利用频率在线变化的多频率正弦电流信号作为电流环给定,搜索伺服机械谐振系统的频率特性,搜索算法控制结构见图4。

图4 频率特性搜索的结构图Fig.4 The structure of searching for frequency characteristic
3.1 多频率正弦转矩电流信号
频率在线变化的多频率正弦转矩电流信号是由多个不同频率的正弦信号组合而成,设频率的搜索范围为[flow,fup],包含的不同频率的正弦信号个数为n0,每个正弦信号间的频率间隔fd为

则多频率正弦电流信号可以用下式表达:
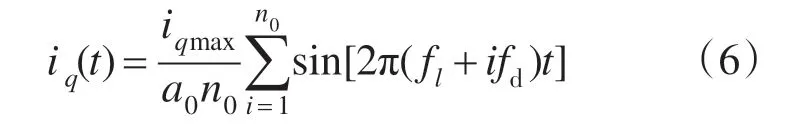
式中:iqmax为电机转矩电流限幅值;a0为调整系数。
通过调节a0保证电机转速在安全运行范围内。
3.2 基于分割搜索区间的谐振频率特性的搜索
利用式(6)所示的多频率正弦电流信号激励系统,对电机转速和反馈转矩电流在线进行采样和存储。由式(2)可以得到在频率f处,谐振环节的幅度增益K与转矩电流,电机转速的关系:
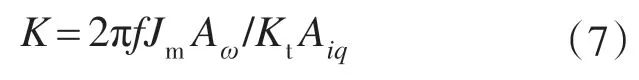
式中:Kt为电机转矩系数;Aω,Aiq分别为频率f 处系统的电机转速和转矩电流的幅值。
根据图2,可以得知在系统反谐振频率和谐振频率处,K 分别取到极小值和极大值。因此频率特性搜索的问题可以转换为在目标频率范围内寻找K的极大值和极小值,以及分别对应的频率和带宽。搜索谐振频率特性的流程如下:
1)根据控制对象初始化多频率正弦电流信号,确定flow,fup,n0,fd,iqmax,a0的值;
2)利用多频率正弦信号激励系统,对电机转速和转矩电流进行FFT变换,得到Aω和Aiq;
3)根据式(7)确定K 的极值点个数np和对应的频率fp。当np=0时,若当前转矩电流信号的频率间隔小于等于频率间隔阈值f1,则该区间收敛,否则,将该搜索区间平均分割为2 个子搜索区间。当np≥1 时,若当前转矩电流信号的频率间隔小于等于频率间隔阈值f2,则该子区间收敛,且极小值点对应反谐振点,极大值点对应谐振点;若当前转矩电流信号的频率间隔在f1与f2之间,可以根据fp将当前搜索区间分割为np个子区间:[fp_1-fd,fp_1+fd],[fp_2-fd,fp_2+fd]…[fp_np-fd,fp_np+fd];若当前转矩电流信号的频率间隔小于等于频率间隔阈值f2,可以根据fp将当前搜索区间分割为2np+1 个子区间:[flow,fp_1-fd],[fp_1-fd,fp_1+fd][fp_1+fd,fp_2-fd],…[fp_np+fd,fup]。在分割完成后,利用式(5)计算得到各个子区间的搜索频率间隔。
4)当仍存在不满足区间收敛条件的频率子区间时,继续重复2)、3)对频率子区间进行分割。否则,结束搜索,确定谐振频率和反谐振频率,并计算得到其增益和谐振带宽。
频率间隔阈值f1和f2的选取需要综合考虑收敛速度和精度的要求。选取较大的f1能有效提高不包含极值的子搜索区间的收敛速度;选取较小的f2则能有效提高包含极值的子搜索区间的搜索精度。
4 陷波滤波器的设计
4.1 陷波滤波器特性分析
无限冲击响应的陷波滤波器在陷波频率处具有较大的幅度衰减和较小的相位滞后,因此,它被广泛地应用到谐振抑制的控制结构中。典型的陷波滤波器的传递函数如下:

在ω0设计合理的时候,伺服机械谐振系统的谐振峰值可以被消除掉。陷波滤波器的带宽一般设计得很小,确保不影响系统在谐振频率附近的特性。但是,由于|GN(jω0)|=0,系统在加入传统陷波滤波器后在谐振点的幅度增益为负无穷大,因此,这种滤波器虽然抑制了机械谐振,但是也恶化了系统的动态响应特性;另外一方面,在实际系统中,机械谐振在谐振点附近对系统幅频特性的影响往往不是对称的,具有对称调整带宽的陷波器并不能完全抵消机械谐振对系统动态特性的影响。因此,可以利用下式的陷波滤波器进一步改善系统的幅频特性,降低谐振环节对系统动态性能的影响。

该滤波器的幅频响应特性见图5,陷波滤波器在谐振频率ω0=2πfr处的幅值增益和带宽分别为
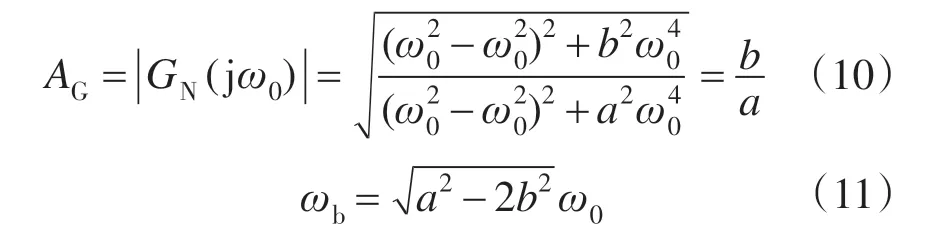
因此,可以根据搜索得到的伺服系统谐振特性确定a 和b,从而设计陷波滤波器,达到抑制伺服系统机械谐振的目的。

图5 陷波滤波器的幅频响应Fig.5 The amplitude-frequency response of notch filter
在上述分析中,尽管陷波滤波器在幅频特性上降低了系统的谐振增益,但是并不能完全抵消系统的谐振环节。所以,优化陷波滤波器的参数可以进一步改善系统的动态响应性能。
图6为机械谐振环节和陷波滤波器的零极点分布。可以看出,在理想情况下,调节b可以使陷波滤波器的零点与谐振环节的极点对消,降低谐振环节极点对系统的影响。

图6 陷波滤波器和谐振环节的零极点分布图Fig.6 The zero-pole of notch filter and resonant part
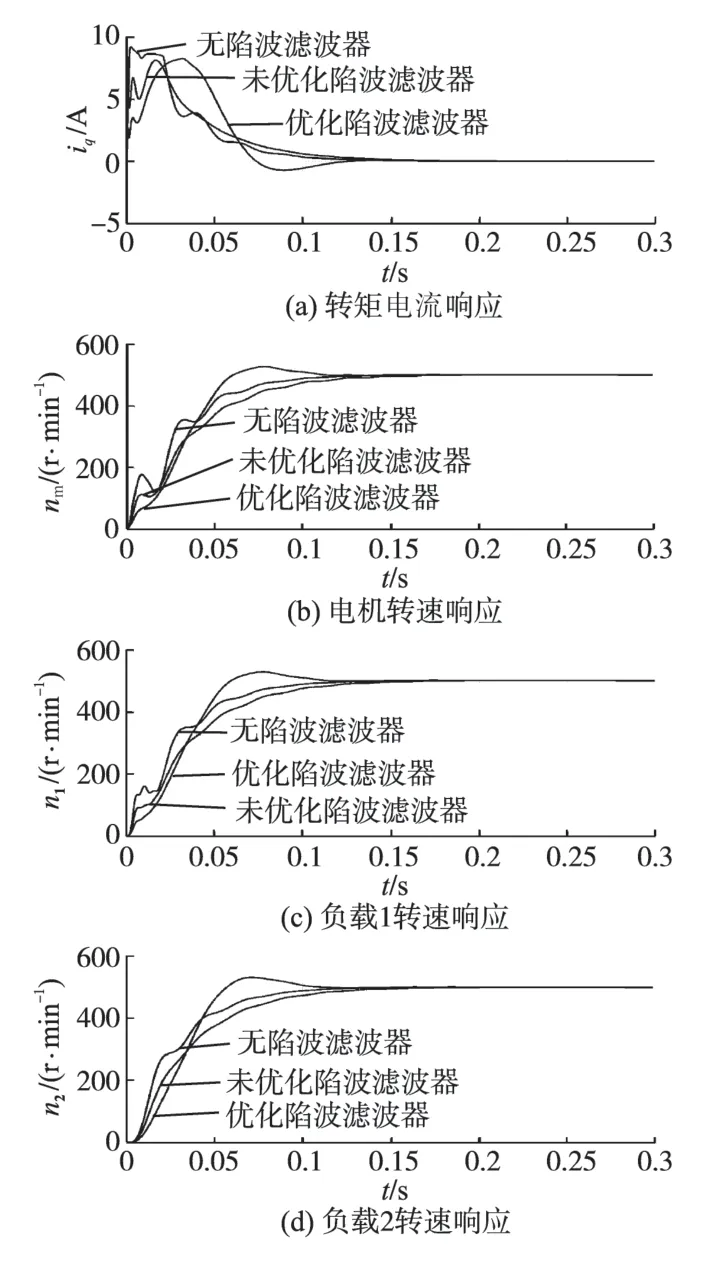
图6 为陷波滤波器GN(s)和机械谐振环节Gr(s)的零极点分布图。由式(9)可知,在0 一个极点会移动到P1点,该极点与谐振环节的零点到原点的距离相同,均为ωan。同时,另一个极点移动到P2点,与原点距离为ωn2/ωan≫ωan。图7为不同滤波器参数下,GN(s)Gr(s)的单位阶跃响应,其中,c1 图7 不同的滤波器参数下,机械环节的阶跃响应Fig.7 The step responses of mechanical part with different filter parameters 4.2.1 设计抑制机械谐振的陷波滤波器参数 根据谐振频率个数确定陷波滤波器个数n,通过在线搜索得到的谐振频率处的幅度增益和带宽,利用式(10)和式(11)推导出陷波器参数与谐振频率特性的关系如下: 4.2.2 优化陷波器参数改善系统动态响应性能 在Matlab/Simulink 仿真环境实现带有PI 结构电流控制器的伺服电机控制仿真系统,其中电流环的PI 参数采用极点配置的方式设计。仿真系统参数配置为:电机惯量Jm=0.004 3 kg·m2,负载惯量J1=0.001 kg·m2,负载惯量J2=0.01 kg·m2,传动刚度Ks1=1 000 N·m/rad,传动刚度Ks2=300 N·m/rad,粘滞阻尼系数Kw1=0.11 N·m·s/rad,粘滞阻尼系数Kw2=0.11 N·m·s/rad,负载侧摩擦转矩Tc=1.23 N·m,电机转矩系数Kt=2.35 N·m/A,电机额定电流In=8.5 A。 根据仿真模型的电气和机械特性初始化多频正弦转矩电流信号,确定频率搜索范围[flow,fup]为[0,300]Hz,包含的频率个数n0为10,频率间隔fd为30 Hz,频率间隔阈值f1和f2分别为10 Hz 和1 Hz。依据前述的搜索算法和陷波滤波器设计方法,对系统频率特性的搜索和机械谐振的抑制分别进行了仿真研究。图8为整个搜索过程中的反馈转矩电流。图9为多频正弦转矩电流信号的搜索范围的变化过程。由仿真结果可以看出,对搜索频率的范围更新4次后,搜索得到了系统谐振频率、反谐振频率、谐振频率处的幅度增益和带宽,搜索结果见表1。系统具有两对较高的谐振频率和反谐振频率。 图8 整个搜索过程中的电机转矩电流响应Fig.8 The simulated response of torque current of motor in the whole search procedure 图9 多频率正弦信号搜索范围的更新过程Fig.9 The updating process of search band of multi-frequency sine signals 表1 搜索得到的谐振频率特性Tab.1 The searched resonance frequency characteristic 根据搜索得到的系统频率特性设计和优化陷波滤波器,此时系统的响应如图10所示。电机转速响应和负载转速响应曲线表明陷波滤波器的加入能够较好地抑制伺服系统的机械谐振;同时,经过参数优化的陷波滤波器能平滑电机转速在动过程中的轻微抖动,从而进一步改善系统的动态响应性能。 在仿真基础上,搭建了由4 400 W 永磁同步电机和弹性传动机构组成的实验平台,其中,传动机构由弹性联轴器和同步带构成。伺服驱动器的主芯片采用TI 的TMS320F2812,三相逆变器的开关频率为10 kHz。电机的转速通过实验电机带有的2 500线增量式光电编码器获取。系统速度环的周期为0.2 ms。实验平台的电气参数和机械参数为电机惯量Jm=4.3×10-3kg·m2;电机转矩系数Kt=2.35 N·m/A;电机额定电流In=8.5 A。 图10 3种不同控制策略的伺服系统的响应Fig.10 Responses of servo system with three different control strategies 根据实验平台的电气和机械特性初始化多频正弦转矩电流信号,然后利用前述的迭代算法对系统的谐振频率特性进行搜索,搜索算法的参数与仿真参数一致,搜索过程中的电机转矩电流响应和电机转速响应如图11 所示。图12 为多频正弦转矩电流信号搜索范围的变化过程。由实验结果可以看出,对搜索频率的范围更新4 次后,搜索得到了系统谐振频率、反谐振频率、谐振频率处的幅度增益和带宽,搜索结果见表2。系统具有一对谐振频率和反谐振频率。利用系统的频率特性设计陷波滤波器对系统的机械谐振进行抑制,伺服系统的响应如图13 所示。 表2 搜索得到的谐振频率特性Tab.2 The searched resonance frequency characteristic 图11 在整个搜索过程,电机转矩电流响应Fig.11 The experiment response of torque current and speed of motor in the whole search procedure 图12 频率正弦信号搜索范围的更新过程Fig.12 The updating process of search band of multi-frequency sine signals 图13 3种不同控制策略的伺服系统的响应Fig.13 Responses of servo system with three different control strategies 由实验结果可知,陷波滤波器有效地抑制了系统的低频振荡;优化后的陷波滤波器能够消除电机在启动过程中出现的抖动,进一步改善系统的动态响应性能。 本文首先提出了一种迭代搜索算法获取系统频率特性,然后根据频率特性设计和优化陷波滤波器,实现了对伺服系统的机械谐振的抑制和动态响应性能的改善。迭代搜索算法能准确得到系统在设计陷波滤波器时需要的频率特性;设计得到的陷波滤波器在有效地抑制系统机械谐振的基础上,进一步改善了系统的动态响应性能。实验和仿真结果验证了算法的有效性。 [1]黄梁松,曲道奎,徐方,等.基于可调惯量比的伺服系统低频谐振控制[J].电气传动,2010,40(7):61-65. [2]杨明,郭少辉,郝亮,等.基于FFT 的PMSM 伺服系统在线定位末端抖动抑制技术[J].电气传动,2013(S):40-43. [3]胡清,童怀.伺服系统机械谐振问题的研究[J].电气传动,2000,30(3):7-11. [4]张瑞成,童朝南.基于状态观测器的轧机主传动系统机电振动控制研究[J].电气传动,2005,35(11):3-7. [5]王浩,郝亮,杨明,等.双惯量弹性系统状态观测器设计与实现[J].电气传动,2013(S):48-51. [6]Szabat K,Orlowska-Kowalska T.Performance Improvement of the Industrial Drives with Mechanical Elasticity Using Nonlinear Adaptive Kalman Filter[J].IEEE Trans.Ind Elec.,2008,55(3):1075-1084. [7]Levin J,Ioannou P.Multi-rate Adaptive Notch Filter with an Adaptive Bandwidth Controller for Disk Drives[C]// American Control Conference.2008:4407-4412. [8]Li G.A Stable and Efficient Adaptive Notch Filter for Direct Frequency Estimation[J].1997,45(8),2001-2009. [9]Lei Gu,Shan-ming Wan,Jicheng Yu,et al.A Novel Method for Shaft Torsional Oscillation.Suppression in Servo Systems[C]//Power Engineering and Automation Conference,2012:1-5. [10]Lee D H,Lee J H,Ahn J W.Mechanical Vibration Reduction Control of Two-mass Permanent Magnet Synchronous Motor Using Adaptive Notch Filter with Fast Fourier Transform Analysis[J].IET Electric Power Applications,2011,6(7):455-461. [11]Wang Wenyu,Xu Jinbang,Shen Anwen.Detection and Reduction of Middle Frequency Resonance for an Industrial Servo[J].Control Engineering Practice,2013,21(7):899-907. [12]杨辉,范永坤,舒怀亮.抑制机械谐振的一种改进的数字滤波器[J].光电工程,2004,12(31):30-39. [13]Koji Sugiura,Yoichi Hori.Vibration Suppression in 2-and 3-mass System Based on the Feedback of Imperfect Derivative of the Estimated Torsional Torque[J].IEEE Trans.Ind Elec.,1996,43(1):56-64.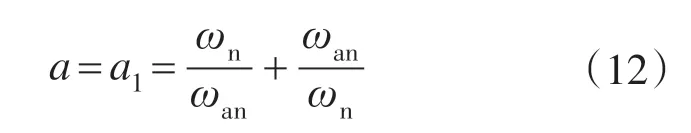
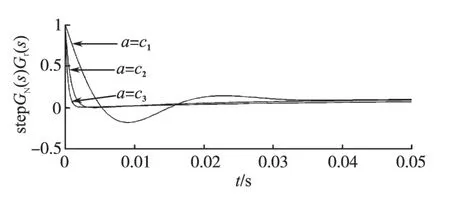
4.2 陷波滤波器的参数设计

5 仿真和实验结果
5.1 仿真结果



5.2 实验结果




6 结论
