基于MPPT的新型变步长增量电导法的研究

高嵩，罗浩，何宁，陈超波

（西安工业大学电子信息工程学院，陕西西安710021）

1 引言

世界能源危机的加剧，使得取之不尽的太阳能资源正在成为全球各国能源转型关注的焦点。太阳能发电系统最大功率跟踪（MPPT）作为光伏阵列的重要控制策略［1］。在很大程度上决定了光电转换效率。通过优化控制策略，使其既能减少对最大功率点的误判，又能实现跟踪速度和精度的提高。

传统的扰动观察法［2］、恒定电压法［3］和电导增量法［4］在工程实际中都存在各自的缺陷［5-7］。本文分析了光伏阵列的工作特性，将变步长与增量电导法相结合，从而减小了由于光照强度变化而产生的超调量和稳态误差，缩短了过渡过程时间，提高了控制精度。在Matlab/Simulink 环境下，利用S 函数对此新型变步长增量电导法设计方案进行了仿真，验证了该理论的正确性。

2 光伏阵列的数学模型

光伏电池可以等效看作一个电流为Ipv的恒流源和一个二极管D并联，Rs和Rsh分别表示电池内部串联和并联电阻。光伏电池阵列模型如图1所示。

图1 光伏电池阵列模型Fig.1 Photovoltaic array model

温度和光照两个影响光伏输出特性的重要因素作近似化处理。Ipv的值等于电池的短路电流。光伏电池阵列的I—U特性关系方程为

式中：I为光伏电池工作电流；Io为反向饱和电流；U 为光伏电池输出电压；q 为电荷常数；T 为绝对温度；A为光伏电池中半导体电池的P-N 结系数；K为波尔兹曼常数。

根据光伏阵列的数学模型，运用Matlab/Simulink进行仿真，图2a为在恒定光照强度1 000 W/m2的情况下，不同的温度所对应的P—U 特性曲线。图2b 为环境温度在恒定25 ℃的情况下，不同的光照强度所对应的P—U特性曲线。

图2 P-U特性曲线Fig.2 P-U Characteristic curves

从图2 可以看出，太阳电池阵列在恒定的温度和日照强度下具有唯一的最大功率点。然而在实际情况中，电池阵列的电压和电流随着温度和光照的变化也在不断发生着变化，导致最大功率点不能持续稳定在固定位置，光伏系统输出功率效率也会因此而降低。

3 常用算法原理分析

关于最大功率跟踪的方法很多，常用的有扰动观察法（Perturb&Observe algorithms，P&O）、恒定电压法（CVT）和增量电导法。下面将对这几种方法的原理和优缺点进行分析比较。

3.1 扰动观察法

扰动观察法也被称为爬山法，算法原理是光伏阵列在工作时，每隔一段时间给光伏阵列的输出电压一个微弱的电压扰动。通过检测光伏阵列的输出电压和电流，计算得到输出功率。再与上一时刻的功率进行比较，确定寻优方向。

3.2 恒定电压法

在外界环境条件变化不大的情况下，最大功率点基本固定在某一电压值附近，即最大功率点电压UM和开路电压UOC之间存在一种近似的线性关系表达式，即UM=KUOC，文献［3］给出了比例系数K的数值，恒定电压法通过不断的对光伏阵列输出开路电压UOC进行采样，然后利用比例系数K求得UM。

3.3 增量电导法

增量电导法是一种基于数学模型的精确寻优算法，其基本原理是通过判断输出电导的变化量和瞬时电导值的大小来决定光伏阵列输出电压变化方向。光伏电池输出功率P=U·I，故dP/dU=d（UI）/du=I+（dI/dU）·U 在最大功率点处，由于dP/dU=0，即I+（dI/dU）·U=0，U=Umaxx当dP/dU>0，即I+（dI/dU）·U>0，得U＜Umax。当dP/dU<0，即I+（dI/dU）·U＜0 得U＞Umax。增量电导法的光伏电池输出P—U特性如图3所示，其揭示了增量电导法应用的数学含义。

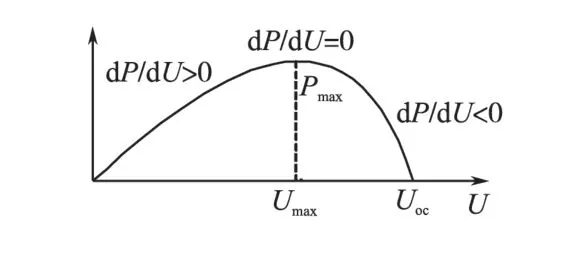
图3 增量电导法输出P-U特性Fig.3 Incremental conductance method output P-U

由图3可知，当外界环境条件一定时，光伏阵列P—U特性曲线存在唯一的最大功率点。

3.4 上述3种方法优缺点对比

扰动观察法由于需要通过不断的扰动来判定是否在最大功率点而因此无法稳定在该点处。恒定电压法的数学模型简单，但由于近似计算Um，对误差也会产生一定程度的放大，并且利用效率降低。增量电导法响应速度快，控制精度高，但是软件实现中对步长值的选择要求较高，否则难以发挥其高跟踪精度的优势。

4 新型变步长增量电导法

为了较好地解决上述问题，并且能够保证在外界环境变化时仍然能够比较平稳的实现最大功率跟踪，本文提出新型变步长增量电导法的理论。

新型变步长寻优最大功率点跟踪如图4解析所示。从图4中可以看出，光伏电池的P—U曲线是不对称的，功率从P1变化到Pm时工作电压从U1增加到Um。功率从P2变化到Pm时工作电压从U2减小到Um。可以看出：

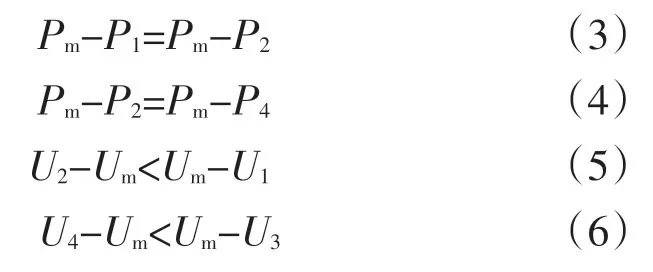
因而，在功率变化ΔP相同，跟踪步数也相同的情况下有：

图4 新型变步长寻优最大功率跟踪Fig.4 The new variable step size optimization maximum power tracking

将dP/dU 转化为I+（dI/dU）·U 的关于电流I和电压U的关系，根据dU和dI的关系，判断当前功率点所在位置在最大功率点Pmax的左侧还是右侧，距离最大功率点的远近，以及向最大功率点趋近的方式和步长值。该算法可以根据其所在位置距离最大功率点的远近，选择不同的步长值，并且在相同功率的情况下，从最大功率点的左右两侧分别向最大功率点趋近的步长也不相等，左侧步长大于右侧步长。

|dU|≤ε可近似认为dU=0，|dI|≤δ可近似认为dI=0。dU=0，dI=0 是一个范围很小的区域，可认为是达到最大功率点的区域。在dU≠0 的情况下，若I+（dI/dU）·U>0，以A·|dP/dU|为步长，趋向最大功率点，若I+（dI/dU）·U≤0，以B·|dP/dU|为步长，趋向最大功率点。在dU=0 的情况下，若dI>0以C·|dI|为步长，趋向最大功率点，若dI≤0，以E·|dI|为步长，趋向最大功率点。其中A，B 为|dU|>ε，在最大功率点左右两侧的步长缩放系数；C，E 为|dU|≤ε，最大功率点左右两侧趋向最大功率点的步长缩放系数。

新型变步长增量电导法算法流程如图5所示。

图5 新型变步长增量电导法算法流程图Fig.5 New variable step algorithm flow chart of incremental conductance method

5 验证实验

5.1 Matlab仿真

为了验证新型变步长增量电导法的理论分析，应用Matlab/Simulink对此方法进行仿真研究验证。本论文首先搭建了光伏太阳能电池板模型，然后搭建了Boost 升压电路，用S 函数编写了MPPT新型变步长增量电导法的算法，对IGBT进行控制，从而实现最大功率跟踪功能。其中，光伏阵列参数Um=35.2 V，Im=4.95 A，Uoc=44.2 V，Isc=5.2 A，a=0.015，b=0.7，Tref=25 ℃，Rs=2 Ω。Boost升压电路中电容C=450 μF，电阻R=12 Ω。选择16 位A/D 转换器对光伏阵列输出的电压和电流值进行采样，再经过输出的电压和电流值进行采样，经过运算放大，在DSPIC33FJ16GS502中对采集的信号进行处理。其中步长缩放系数A，B，C，E均由电压和电流的量程范围以及A/D转换器的精度所决定。其中A＞B，C＞E。M=A/B，N=C/E 的比例关系由P—U拟合曲线确定。系统的仿真模型如图6所示。

5.2 仿真验证和仿真结果对比

未介入最大功率跟踪（MPPT），温度25 ℃，光照强度由1 000 W/m2降到800 W/m2，再恢复到1 000 W/m2。功率仿真如图7所示。

图6 MPPT仿真模型Fig.6 MPPT simulation model

由图7 可以看出，未介入最大功率跟踪（MPPT），即便是在光照稳定的情况下，输出功率很不稳定而且谐波含量比较高。在光照强度发生变化时，过渡过程时间较长。

在MPPT 的控制中，运用传统增量电导法对于最大功率点进行跟踪，其光照强度由1 000 W/m2降到800 W/m2，再上升到1 000 W/m2。功率仿真如图8 所示。从中可以看出，介入普通增量电导法之后，波形较图7相比，输出功率较为稳定。但是光照变化，过渡过程时间还是偏长，谐波含量偏高。

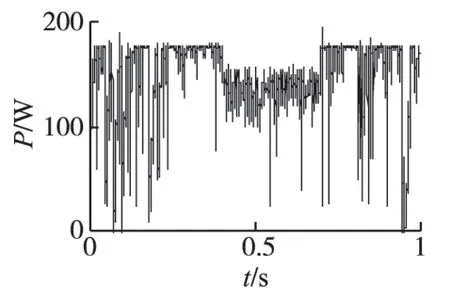
图7 未介入MPPT的功率仿真Fig.7 Did not intervene in MPPT power simulation

图8 传统增量电导法功率Fig.8 Traditional incremental conductance power

在MPPT 的控制中，运用新型变步长增量电导法对于最大功率点进行跟踪，温度恒定在25 ℃，其光照强度由1 000 W/m2降到800 W/m2再上升到1 000 W/m2。图9 是不同光强下功率、电压、电流跟踪效果图。功率仿真如图9a 所示，电压仿真如图9b 所示，电流仿真如图9c 所示。

由图9 可得，介入新型变步长增量电导法之后，当光照在1 000 W/m2时，过渡过程时间由原来的0.15 s 缩短到0.05 s，输出功率稳定在160 W，当光照在0.4 s突变为800 W/m2时经过短暂的0.02 s过渡时间，达到输出稳定，输出功率稳定在130 W。在0.7 s光照强度再次恢复到1 000 W/m2，经过0.05 s，功率恢复为160 W。电压在光照1 000 W/m2时为43 V，光照突变到800 W/m2时，电压经过0.02 s 稳定在40 V，光照再次跳变到1 000 W/m2，电压经过0.05 s 恢复为43 V。电流也是稳定在由3.7 A 变化到3.3 A，再变化到3.7 A。整个过程中超调量较低，谐波含量较低，功率、电压、电流输出稳定，符合工业现场应用条件。25 ℃条件下，对比各种控制方法在光照发生变化时，过渡过程时间如表1所示。

图9 不同光强下功率、电压、电流跟踪效果图Fig.9 The power，voltage and current under different light intensity tracking effect

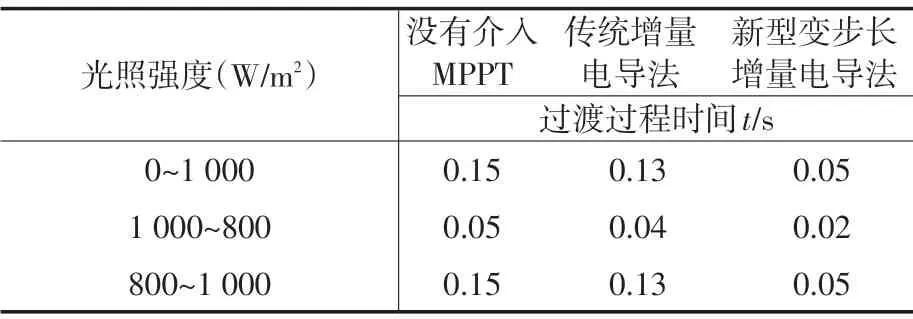
表1 过渡过程时间表Tab.1 The transition process time

为了更进一步验证此算法的正确性和对于环境的适应能力，仿真系统模拟外界环境温度为10 ℃和40 ℃，光照强度均由1 000 W/m2在0.4 s降为800 W/m2，再在0.7 s 降为600 W/m2，新型变步长增量电导法对于最大功率跟踪的情况。图10a为温度10 ℃时，输出功率仿真图；图10b为温度40 ℃时，输出功率仿真图。

图10 输出功率Fig.10 The output power

由图10可知，在0～50 ℃范围内，光照一定的情况下，温度越低，所对应的输出功率越高。这符合光伏的P—U特性曲线。从中也可以看出无论是在25 ℃标准状况环境下，还是在10 ℃，40 ℃，新型变步长增量电导法都可以高效率而且迅速准确的对最大功率点进行跟踪。

6 结论

通过对光伏阵列最大功率跟踪的理论分析，本文提出的“新型变步长增量电导法”满足光伏阵列的P—U 特性曲线要求，并由Matlab/Simulink 的仿真数据可以证明该方法对于光照的实时变化具有跟踪精度高，输出功率稳定等优点。对于较大范围内的温度变化，同样具有快速跟踪最大功率点，抗干扰能力强等特性。仿真和实验结果均保证了该方法的正确性和可行性。

［1］茆美琴，余世杰，苏建徽.带有MPPT 功能的光伏阵列Matlab 通用仿真模型［J］.系统仿真学报，2005，17（5）：1248-1251.

［2］吴理博，赵争鸣，刘建政，等.具有无功补偿功能的单级式三相光伏并网系统［J］.电工技术学报，2006，21（1）：28-32.

［3］李晶，窦伟，徐正国，等.光伏发电系统中最大功率点跟踪算法的研究［J］.太阳能学报，2007，28（3）：268-273.

［4］陈兴峰，曹志峰，许洪华，等.光伏发电的最大功率跟踪算法研究［J］.可再生能源，2005（1）：8-11.

［5］马桂龙，付青，陈淑华.基于自适应预测算法的光伏系统MPPT 技 术 研 究［J］.太 阳 能 学 报，2012，33（12）：2062-2067.

［6］刘栋，杨苹，黄锦成.一种光伏发电系统变步长MPPT 控制策略研究［J］.电气传动，2011，41（4）：35-38.

［7］潘雷雷，李国丽，胡存刚.新型占空比直接控制的光伏MPPT 研究［J］.电气传动，2011，41（7）：25-29.

［8］Hsu C Y，Wu H Y.A New Single-phase Power Filter with Reduced Energy-storage Capacity［J］.IEEE Proc，Electr，Power，1996，143（1）：25-30.

［9］Komurcugil H.Steady-state Analysis and Passivity-based Control of Single-phase PWM Current-source Inverters［J］.IEEE Transactions on Industrial Electronics，2010，57（3）：1026-1030.