基于扩展prony算法的小电流单相接地故障选线

张岭峰，唐麒皓，张庆华

(1.大庆油田有限公司电力集团电力营销公司，黑龙江 大庆 163000;2.东北石油大学 电气信息工程学院，黑龙江 大庆 163318;3.大庆采油三厂试验大队北十四聚合物配制站变电所，黑龙江 大庆 163000)

0 引言

由于中性点非有效接地系统发生单相接地故障时接地的电流一般不会超过10 A，所以又将其称为小电流接地系统。单相接地故障发生时，由于小电流接地系统的三相电压仍满足对称关系，使得系统能够继续供电。其较高的供电可靠性使其广泛地应用于110 kV及以下的配电网中［1］。

由于单相接地的短路电流很小，无法使过流继电器发生动作，因此小电流接地系统单相接地故障选线的实现是较难实现的。110 kV及以下的配电网中，单相接地故障在所有故障类型中是最容易发生的，约占80%左右。因此小电流接地系统单相故障选线的研究具有重大的应用价值［2］。到目前为止对于单相故障的选线主要方法有两类，一类是利用单一的特征量进行判断，它包括基于零序电流，负序电流和外加信号三种方法，这三种方法都不能准确的实现故障的选线，因此具有一定的局限性。另一类是将上述三种单一特征量进行组合，形成多重判据，因此大大提高了选线精度。

1 扩展prony算法的分析

以指数函数作为扩展prony算法的数学模型，其函数的离散形式如式(1)所示:

其中 bi=Aiexp(jθi)，zi=exp［(αi+j2πfi)Δt］。

Ai—幅值;θi—相位;αi—衰减因子;fi—震荡频率;Δt—采样间隔。

扩展prony算法的实现共有五步，方法如下:

(1)给出样本函数的定义式，如式(1)所示，

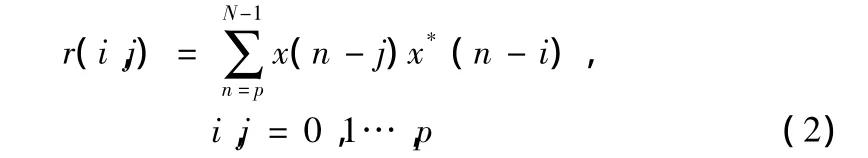
基于样本函数的定义式进行矩阵Re的构造

(2)利用奇异值分解总体最小二乘法(SVD-TLS)算法确定矩阵Re的有效秩p，并对衰减系数α1，…，αp进行总体最小二乘估计。

(3)对特征多项式1+α1z-1+…+αpz-p=0的根 z1，…，zp进行求取，并在条件下用公式i)，i=0，1，…，N-1 求得

(4)利用关系式(5)可以很容易地对b进行求取:

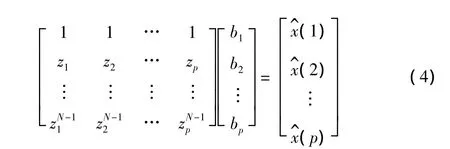
(5)用式(5)确定幅值 Ai，相位 θi，频率 fi和衰减因子 αi的值。

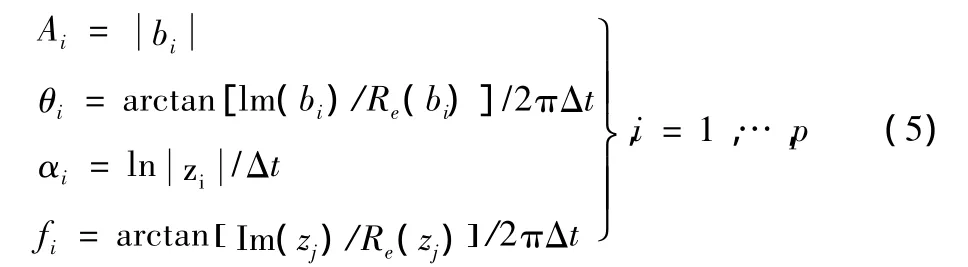
2 单相接地系统故障分析

2.1 单相接地稳态的特点

当电源和负荷中性点均不接地的系统正常运行时，系统每一相对地都存在等效值为C0的电容［3］。因为每一相都有相电压，随之会有一个超前90°的电流流入大地，因此流过三相对地电容的电流的和为零。当A相出现接地短路故障时，该相的对地等效电容和电压将为零，而正常工作的B、C两相的电压将为原来的倍。由图1不难看出，发电机 C0G，C0Ⅰ，C0Ⅱ、线路Ⅰ、Ⅱ的对地总电容如图中的电容所示。当线路Ⅱ的A相发生接地故障后，图1中“→”表示电容电流的分布。

图1 系统单相接地的电流分布图

图1所示的线路Ⅰ没有接地故障，线路Ⅱ的A相发生了接地短路故障，B、C两相的电容电流值和有效值分别如式(6)、(7)所示。这个电流还要从线路Ⅱ的A相流回系统，所以从A相流出的电流为它的负值。

因此在故障线路Ⅱ始端流过的零序电流值和其有效值如式(8)、(9)所示:

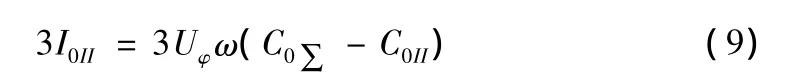
通过以上分析可以得出中性点不接地系统故障线路的零序电流为整个系统非故障元件对地电容电流的和，发生接地故障线路的电容无功功率是从线路流向母线，非故障线路则是从母线流向线路［4］。当线路采用经消弧线圈接地时，发生单相接地故障时系统电流的分布相比于中性点不接地系统有很大的变化。主要原因在故障点处有一个电感分量的电流，由于消弧线圈的补偿导致短路电流减小。且容性无功功率的流动方向和非故障线路的方向一致都是从母线流向线路。因此只能通过零序电流的暂态分量来确定故障线路。

2.2 单相接地过渡过程的特点

绝缘击穿是电网系统发生单相故障的主要原因［5］。中性点不接地系统的过渡过程的等效电路如图2所示。通过图2可以看出忽略Lk后，上述电路就是一个R、L、C串联回路，通过这个电路对暂态电容电流和零序电压u(t)的过渡过程进行分析。流过故障点电流的变化形式随网络参数R、L、C的变化而改变，当电流的过渡过程呈周期性衰减，当时，电流经非周期衰减而趋于稳态值［6］。由分析可知，小电流接地系统的零序电流的主要特征体现在电流的基频和自由振荡频率上［7］。扩展prony算法可以有效地分解出小电流自由振荡频率下的正弦函数，有利于故障确定和选线。

图2 过渡过程的等效网络

3 MATLAB仿真分析

用MATLAB建立仿真模型，线路模型采用Distributed Parameters Line模型，母线引出5条电压为10 kV的出线电源［8］，线路长度分别为L1=18 km，L2=20 km，L3=10 km，L4=16 km以及L5=6 km。线路的正序电阻、正序电感和正序电容分别为0.17 Ω/km、1.171 4 ×10-3H/km 和12.7 ×10-9F/km;零序电阻、零序电感以及零序电容值分别为0.228 Ω/km、3.095 6 ×10-3H/km 和7.751 2 ×10-9F/km。

当过渡电阻为0 Ω，线路1的末端在相电压为最大值时发生A相接地故障。从图3和表1可看出，故障线路上零序电流的基频和自由振荡成分的幅值均达到最大值，其相位与无故障线路相差约180°。因此可以对零序电流的基频和自由振荡成分的相位和幅值进行提取，相位与其他线路相差大于90°的线路即为故障线路。

表1 中性点不接地，接地电阻0 Ω

图3 中性点不接地，接地电阻为0 Ω时各线路波形

当过渡电阻的数值增加时，自由振荡成分将不会表现出明显特征。以100 Ω的过渡电阻为例，由图4和表2可以看出正常线路与故障线路的自由振荡成分的频率会有明显差别，故障线路的自由振荡和基频成分的幅值依然可以满足等于其余正常线路的幅值和。接入电阻的幅值增加到200 Ω时，扩展的prony算法依然可以保证零序电流基频成分幅值和相位的准确性，若继续增加接入电阻阻值则只能使用基频特征实现选线。

图4 中性点不接地，接地电阻为100 Ω时各线路波形

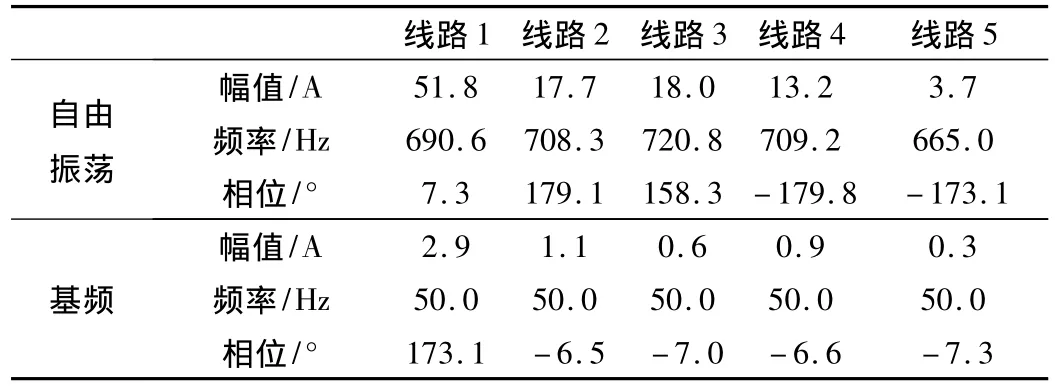
表2 中性点不接地，接地电阻100 Ω

4 结束语

通过对故障的特点进行详细的分析可以发现，小电流接地系统在发生单相接地故障时依然可以进行一段时间的稳定运行，这就为扩展prony算法的应用提供了可行性。利用扩展prony算法可以准确地对自由振荡和基频成分特征进行提取，并在一定程度上提高了抗干扰和噪声的能力。由仿真结果可以看出扩展prony算法可以有效地对单相接地故障进行准确地选线。

［1］邱世卉.一种新的配电网小接地电流故障选线监测方法［J］.科学技术与工程，2012，12(28):7402-7407.

［2］任建文，孙文武，周明，等.基于数学形态学的配电网单相接地故障暂态选线算法［J］.电力系统自动化，2008，32(1):70-75.

［3］尹德昌，赵峰.10 kV配电网单相接地故障选线与仿真研究［J］.科学技术与工程.2013，13(6):1609-1616.

［4］张新慧.基于Prony算法的小电流接地故障暂态选线技术［D］.济南:山东大学，2008.

［5］李冬辉，史临潼.非直接接地系统单相接地故障选线方法综述［J］.继电器，2004，32(18):74-78.

［6］贾鹏飞.基于MATLAB仿真的中性点不接地系统单相接地故障分析［J］.科学技术与工程，2012，12(33):9038-9041.

［7］李清.浅析线路微机保护装置中的小电流接地选线功能［J］.广西电业，2008，9(102):101-104.

［8］司春旺，宋家骅，张涛，等.基于暂态故障测度的小电流接地系统单相接地故障的选线方法［J］.吉林电力，2007，35(4):18-22.