百万千瓦汽轮发电机失磁异步特性研究
2015-06-26王道元徐余法梁旭彪钟后鸿
王道元,徐余法,梁旭彪,钟后鸿
(1.上海电机学院 电气学院,上海 200240,2.上海汽轮发电机有限公司,上海 200240)
0 引言
随着发电机单机容量日益增大、励磁环节日益复杂,发电机失磁故障的发生率高[1]。失磁故障主要包括部分失磁和完全失磁两种形式,其中部分失磁是指励磁系统实际提供的励磁电压少于发电机静稳极限所需的励磁电压;完全失磁则指发电机完全丧失励磁能力。而汽轮发电机失磁异步运行,是指发电机因某种原因失去励磁后,仍带一定有功功率以低转差并在电网中继续运行,这是一种非正常运行方式[2]。汽轮发电机失磁后允许在一段时间(一般为15 min~30 min)内异步运行,让机组运行人员在这段时间内查找失磁故障,排除故障,重新恢复励磁实现再同步,这对于提高电力系统的稳定性和发电机本身的安全稳定运行有着十分重要的作用。
文献[3]依据各模块处于稳态情况下的数学方程,基于MATLAB/Simulink软件工具搭建系统仿真图形,分析水轮发电机失磁故障下的动态特性;文献[4]基于不同模型的同步发电机,考虑多种非线性因素,利用有限元仿真,与数学建模仿真结果比对,得出更为准确的失磁仿真结果。文献[5]基于MATLAB/Simulink仿真软件,以软件本身的模块搭建单机无穷大系统,根据失磁故障模型,研究不同失磁情况下的发电机失磁异步运行过程。本文基于MATLAB/Simulink操作平台,考虑绕组间互漏抗的作用,建立六绕组的同步发电机数学模型,以模块化建模为基础,搭建发电机失磁异步运行仿真模型,分析失磁过程中的物理特性。
1 系统模型的建立
1.1 同步发电机的数学模型
1.1.1 同步发电机的基本组成[6]
同步发电机是旋转的铁磁性元件,绕组结构和动态性能均十分复杂,还包括原动机、调速器和励磁系统,因此应对其作较深入的分析,以便建立研究电力系统各种物理问题的同步发电机数学模型。
同步发电机坐标采用dq0坐标描述,如计及同步发电机转子的动态性能以及原动机、调速器和励磁系统的影响,则仿真计算中发电机的各部分关系如图1所示。
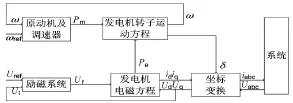
图1 发电机系统结构
1.1.2 同步发电机的数学方程
发电机失磁异步运行时,转子因切割气隙磁场而在转子铁芯中产生涡流,涡流的存在使磁通和电流集中在靠近表面[7],本文将考虑涡流损耗的影响,同时为保证建模的准确性,计及绕组间互漏抗的影响,采用六绕组PARK方程建立同步发电机数学模型。方程表示如下:
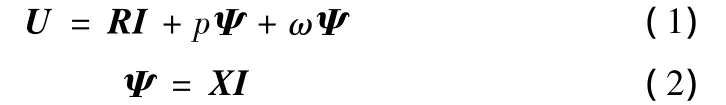
式(1)、(2)中 U、I、R、X、Ψ、ω 分别表示电压、电流、电阻、电抗、磁链和角速度的向量形式。
其中
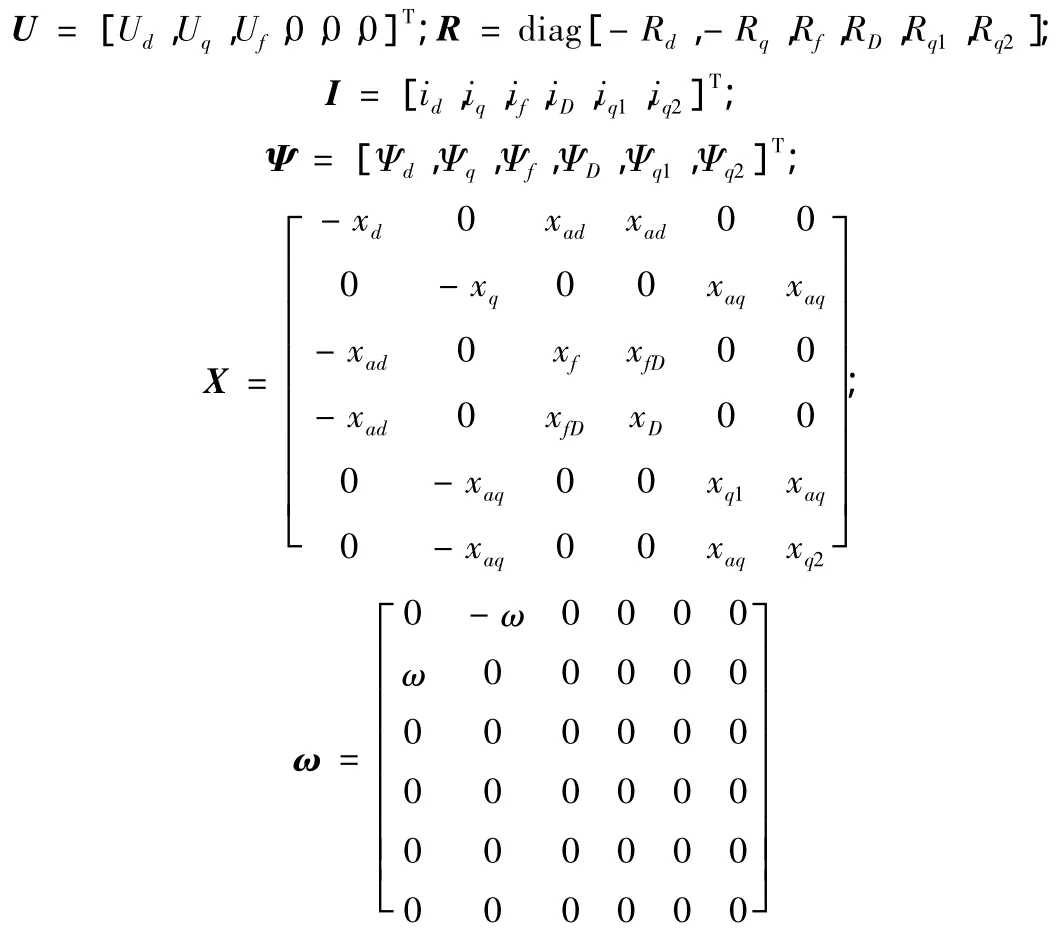
上述向量中的 d、q、f、D、q1、q2分别表示纵轴绕组、横轴绕组、励磁绕组、纵轴阻尼绕组、横轴阻尼绕组和横轴涡流绕组。文中所用各变量均以标幺值表示。
发电机电磁转矩方程为:
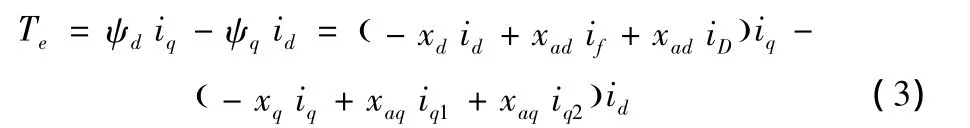
发电机转子运动方程为:
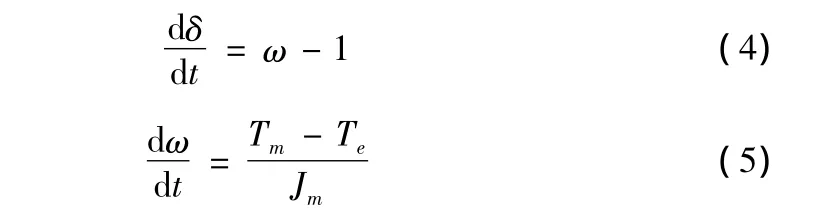
式中ω为转子机械角速度;Tm为原动机输入的驱动转矩;Te为发电机电磁转矩;Jm为机组转动惯量;δ为发电机转子功角。
利用上述数学方程,采用MATLAB/Simulink软件工作平台,依据U、I、溅方三者之间的方程关系搭建同步发电机数学模型如图2所示。
1.2 调速系统数学模型
本文采用文献[8]中所提供的调速系统传递函数框图,如图3所示。

图2 发电机数学模型

图3 调速系统数学模型
1.3 励磁系统的数学模型
本文所选用的励磁系统是由国际电气与电子工程师协会(IEEE)于1992年提出的。励磁系统数学模型框图如图4所示。
1.4 输电线路数学模型
考虑发电机为理想电机,运行过程中不计及谐波对输电线路的影响,忽略线路零序分量的影响,通过坐标变换得其数学方程为:
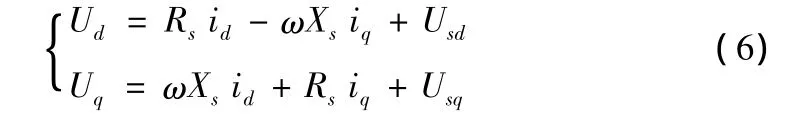
式中Us为电网电压(文中电压均以标幺值表示,故Us取1);Usd、Usq分别为Us在d轴、q轴上的分量;δ为发电机功角;Rs和Xs分别表示输电线路的等效电阻和等效电抗。
基于MATLAB/Simulink软件平台,依据各元件的数学方程和单机-无穷大系统示意图,以模块化建模的方法,搭建整个系统仿真模型,如图5所示。
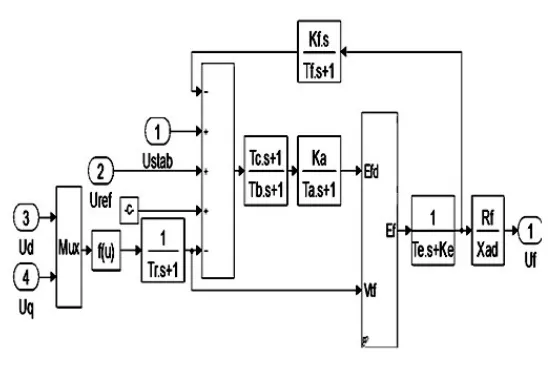
图4 励磁系统数学模型
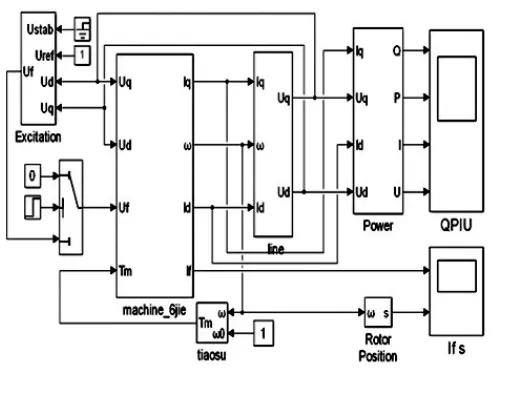
图5 系统仿真图
2 失磁故障类型
如图6所示为发电机励磁系统工作原理图。机组正常运行时,灭磁电阻Rm和分压电阻Rb不参与调节作用,即K1、K2闭合,K3、K4断开。当发生失磁故障时,根据电阻的调节作用和开关的动作情况,得到不同的失磁故障模型,分别建立励磁绕组部分失磁、开路失磁、经灭磁电阻闭合短路失磁故障类型。
Lfd为励磁绕组电抗;Rf为励磁绕组电阻;Rm为灭磁电阻;Rb为部分失磁工况仿真时的分压电阻。
(1)励磁绕组直接短路失磁时,开关K1、K3断开,K4闭合,使K4、Rf、Lfd组成闭合回路,此时励磁电压Uf为0,故可得励磁电压方程为:pΨf+Rfif=0
仿真过程中,故障发生时刻,直接将励磁电压Uf输入为0即可。
(2)励磁绕组开路失磁时,开关K1、K3、K4断开,K2闭合,发生故障时可看作突然向励磁绕组中串联一个无穷大电阻R∞,仿真中取值R∞=1 000 Rf,可得励磁电压方程为:pΨf+ ( Rf+R∞)if=Uf
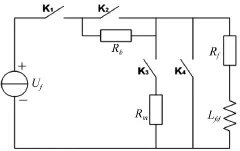
图6 失磁仿真模型
仿真过程中,故障发生时刻,将Rf+R∞等效为Rf代入计算。
(3)励磁绕组经灭磁电阻闭合短路失磁时,开关K1、K4断开,K3闭合,此时K3、Rf、Rm、Lfd组成闭合回路,仿真中取值Rm=5 Rf,可得励磁电压方程为:pΨf+ ( Rf+Rm)if=0
仿真过程中,故障发生时刻,将Rf+Rm等效为Rf代入计算。
3 仿真过程
本文采用百万千瓦火电两级汽轮发电机为例,极对数为1,功率因数为 0.9。利用上述建立的数学方程及Simulink软件搭建仿真模型,研究发电机在励磁绕组直接短路和开路两种故障情况下的失磁动态特性。假设失磁前发电机处于额定运行状态,1 s时刻发生突然失磁故障。
3.1 仿真波形
根据图6失磁故障类型,分别模拟仿真发电机励磁绕组短路和开路两种故障形式,仿真录取波形如图7、8所示。图形物理量均以标幺值表示。
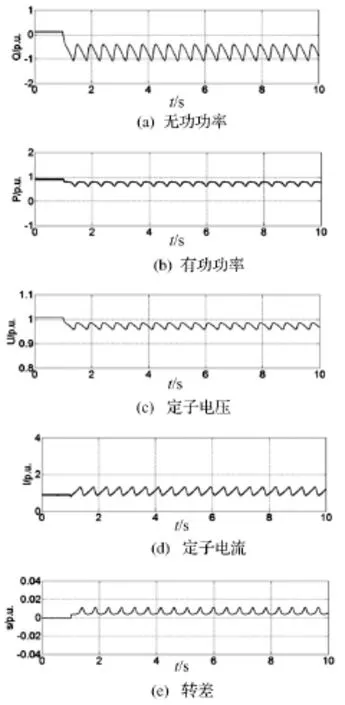
图7 励磁绕组开路失磁
3.2 结果分析
(1)综合图形得出:发生开路失磁时,发电机经过较短的时间进入异步运行;发生短路失磁时,发电机则要经过较长的时间转入异步运行。比较可得,开路失磁故障时,发电机可以迅速进入异步运行,降低了对发电机的危害程度,允许对外做功向电网输送能量。
(2)不管何种失磁方式,发电机的有功功率将减小,定子电压降低;随着励磁系统的励磁能力逐渐减弱,发电机将从电网吸收大量无功功率建立磁场,以实现定转子之间的有效联系,此时发电机的定子电流将增加,可能超过定子侧电流检测装置的允许值,而损坏定子端部绕组。
4 结束语

图8 励磁绕组短路失磁
本文采用百万千瓦火电两级汽轮发电机建立仿真模型,分析发电机励磁绕组处于开路和直接短路两种故障类型下的失磁异步特性。通过比较开路失磁和直接短路失磁两种情况,表明开路失磁时各物理量的变化范围小,允许异步运行,在实际的失磁故障中,可以选择向励磁回路中串联一个无穷大电阻使发电机进入开路失磁故障状态,此时发电机对电网继续输送能量,保证发电机与电网之间的运行稳定。
[1]张学庆,刘波,叶军,等.储能装置在风光储联合发电系统中的应用[J].华东电力,2010,39(12):1894-1896.
[2]汪耕,李希明.大型汽轮发电机设计制造与运行[M].2版.上海:上海科学技术出版社,2008.
[3]钟慧荣,周云海,钟军,等.基于MATLAB/Simulink的水轮发电机失磁动态过程仿真[J].水电自动化与大坝监测,2004,28(4):18-21.
[4]许国瑞,赵海森,宋美红.不同模型的同步发电机失磁异步运行分析[J].陕西电力,2013,41(3):32-35,45.
[5]张建涛,胡刚.汽轮发电机失磁异步运行仿真分析[J].上海大中型电机,2014,57(4):35-38.
[6]倪以信.动态电力系统理论和分析[M].北京:清华大学出版社,2002.
[7]杨嗣彭.同步发电机运行方式的分析[M].1版.成都:成都科技大学出版社,1989.
[8]黄家裕,陈礼义,孙德昌.电力系统数字仿真[M].北京:中国电力出版社,2003.
