基于空间几何模型的创意折叠桌设计加工参数分析
2015-06-24朱慧君朱晓煜吴诗行朱家明
朱慧君,朱晓煜,吴诗行,朱家明
(1.安徽财经大学工商管理学院安徽·蚌埠233030;2.安徽财经大学统计与应用数学学院安徽·蚌埠233030)
基于空间几何模型的创意折叠桌设计加工参数分析
朱慧君1,朱晓煜2,吴诗行2,朱家明2
(1.安徽财经大学工商管理学院安徽·蚌埠233030;2.安徽财经大学统计与应用数学学院安徽·蚌埠233030)
针对创意折叠桌的设计加工参数最优问题以及动态变化过程的分析,以将空间几何转化为平面几何为切入点,分别构建空间几何、稳定性分析以及图形拼接等模型,使用Matlab、Excel等软件编程,得到最优设计加工参数以及动态变化示意图,最后可根据顾客需求设计任意创意折叠桌。
折叠桌 空间几何 受力分析 灵敏度分析 Matlab
创意平板折叠桌设计出自荷兰设计师罗伯特之手,从错综复杂的自然形式中寻找灵感,能使一个平面表面能优雅的飞变成造型独特的家具,美观的直纹曲面外形,设计简约且实用,创新的铰链系统也保证了家具重量轻、易于变形、且坚固。这样一个有创意的家具给我们的生活带来了无限的乐趣,本文将通过分析折叠圆桌的设计原理,也尽力设计出更具有创意的作品,以满足更多顾客需求。
一、给定长方形平板尺寸下折叠桌的设计加工参数
给定长方形平板尺寸为120cm×50cm×3cm,每根木条宽2.5cm,连接桌腿木条的钢筋固定在桌腿最外侧木条的中心位置,折叠后圆桌的高度为53cm。建立空间几何模型[1]描述此折叠桌的动态变化过程,并在此基础上给出折叠[2]桌的设计加工参数(例如,桌腿木条开槽的长度等)和桌脚边缘线的数学描述。
(一)空间几何模型
1、模型的准备
首先,我们以折叠圆桌面的圆心为坐标原点建立空间直角坐标系如图1-1。由于折叠圆桌[3]的对称性,可通过分析圆桌处于第一卦限部分的结构来反映总体的变化情况。根据题中已知条件,将以桌面直径为50cm进行分析。
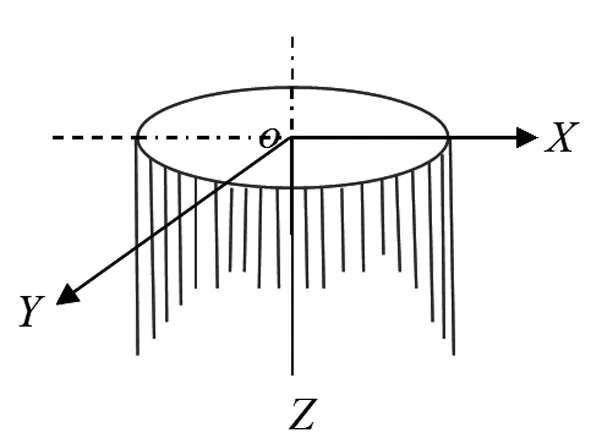
图1-1 空间直角坐标图

图1-2 圆桌实体图
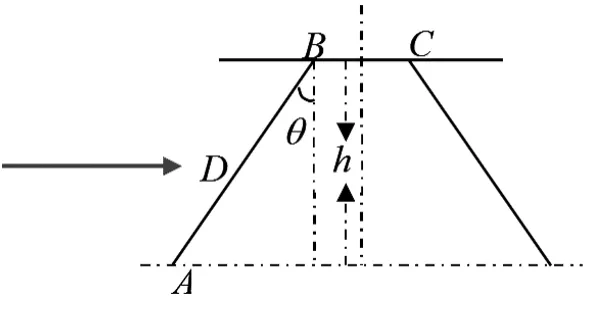
图1-3 切面图
由题目中已知条件及视频资料可以推算出:BC=8cm,AB=56cm,
其中D点为最外围桌腿的钢筋位置,同时也是钢筋在槽内滑动的轴点,轴点坐标为:
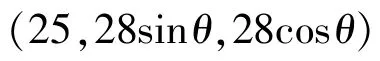
2、模型的建立
从最中间的桌腿沿x轴方向做切面,得到第一卦限部分切面图形如下图1-4。
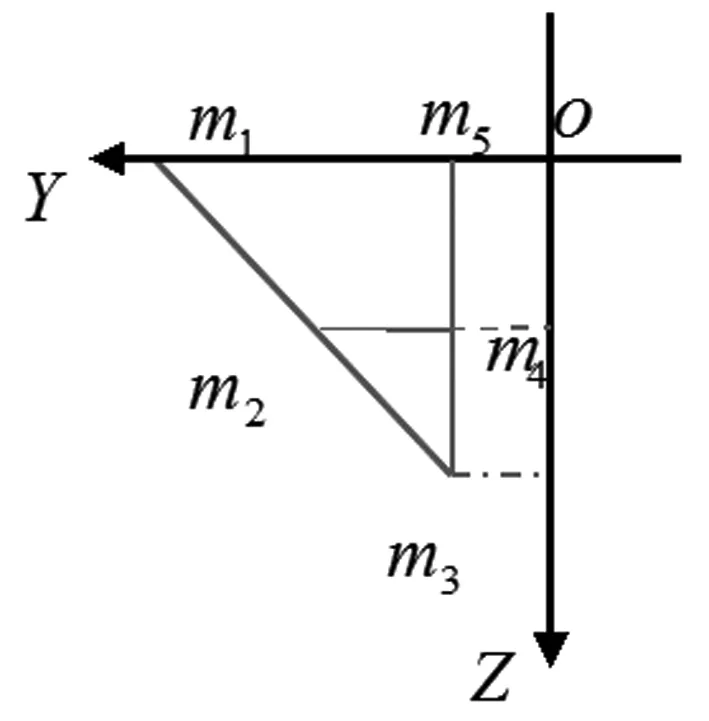
图1-4 平面直角坐标图
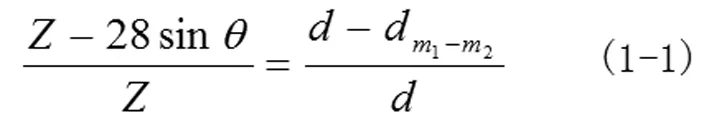
又因为、、三点都位于一条直线上,故有:

3、模型的求解
根据题目建立的直角坐标系,由于创意折叠桌的对称性,可通过对圆桌处于第一卦限部分的结构分析来反映总体的变化情况,故以第一卦限的十组数据为研究对象。为了方便计算,本文取每个木条与桌边切线线段的中点为坐标点,可知:
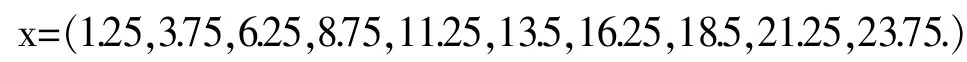
通过圆桌的圆形方程计算可得
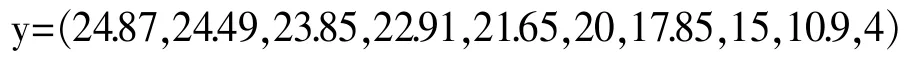
由题目中已知桌高:h=53cm,
其中dm1-m2是由m1、m2、的两点坐标求得,
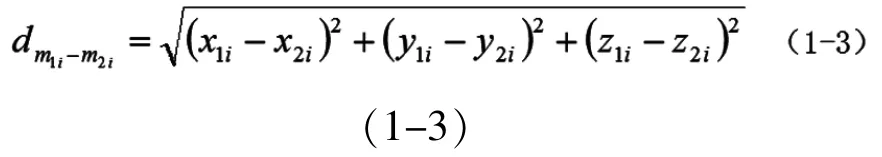
最后算出各桌脚对应的桌脚边缘线上点坐标值及其对应的槽长为表1-1。
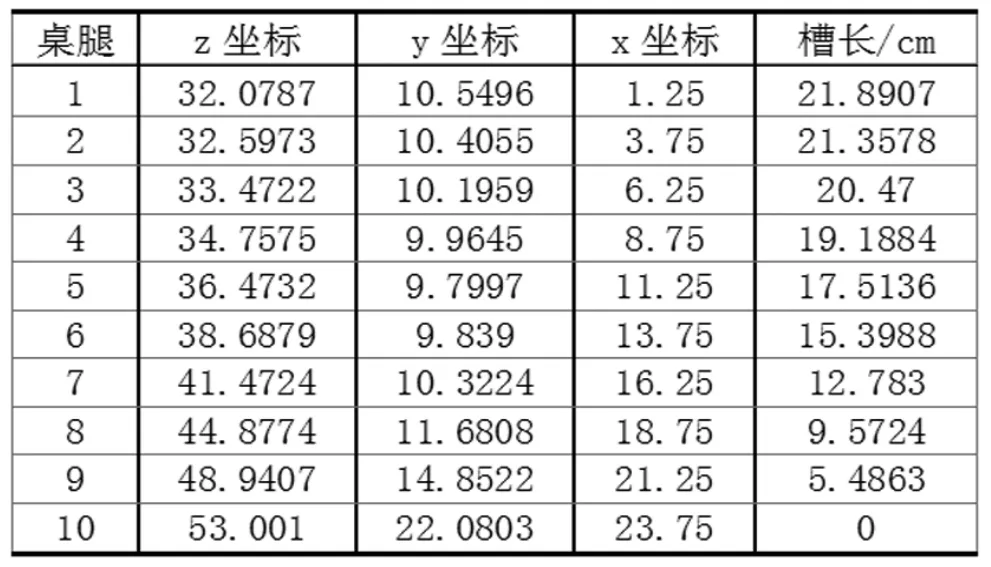
表1 -1各点坐标值及槽长
根据表1-1中桌脚边缘线上的点,在三维空间坐标系中绘制出桌脚边缘线的曲线图,如下图1-5。
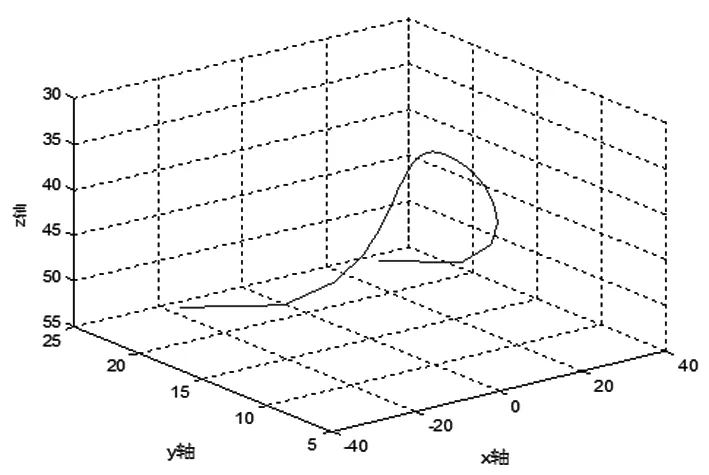
图1-5 空间桌脚边缘线

图1-6 x-z面投影
从图1-5中可以看出桌脚边缘线在空间中形态是:随着纵坐标的增加,竖坐标变化量在递增。再将空间中的桌脚边缘先投影在x-z面上,如图1-6所示,呈现出一条抛物线的形式。故桌角边缘线在空间中类似一条向x-z面渐近的抛物线。
再由求出的桌边各点坐标以及桌脚边缘线各点坐标,利用Matlab软件编程[4]可得创意折叠桌展开时的动态过程,如图1-7。
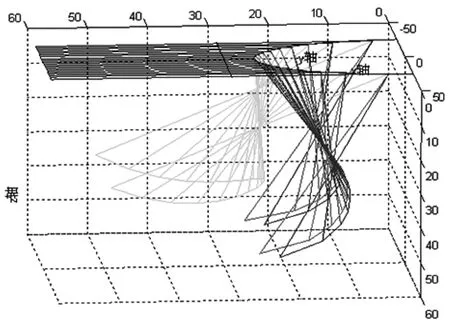
图1-7 折叠桌展开示意图
从图1-7可以清晰地看出创意折叠桌是如何展开的,并且可以看到每一根木条的变化趋势以及每个木条之间夹角的变化。即:中间木条与最初位置的夹角是从0°到90°再变成一个钝角;外侧木条与最初位置的夹角是从0°向90°靠近,但永远不可能达到90°。
二、任意给定折叠桌高度和圆形桌面直径下的最优参数设计
对于任意给定的折叠桌高度和圆形桌面直径的设计要求,讨论长方形平板材料和折叠桌的最优设计加工参数折叠桌的设计应做到产品稳固性好[5]、加工方便、用材最少。将对于桌高70cm,桌面直径80cm的情形,确定最优设计加工参数。
(一)问题的求解
已知桌面高度和桌面半径,通过将立体几何转化为平面几何的方法求出设计加工参数。再通过受力分析的方法得到折叠桌达到最稳固状态时对折叠桌相关参数的要求(比如夹角大小)。最后分析裁剪木条宽度与桌面宽度之间的比例关系以及平板材质对折叠桌加工方便和用材最少的影响。
2.1.1 折叠桌的稳固程度
(1)轴点受力平衡
从物理学知识可知当轴点处于受力平衡时,物体可以保持平衡状态,通过分别研究为任意值时的受力分析情况来确定折叠桌的稳固性最优的状态。为了便于受力分析,在图1-4的基础上将最短桌腿和最长桌腿在面上的投影集中在一张平面图上,即图2-1。
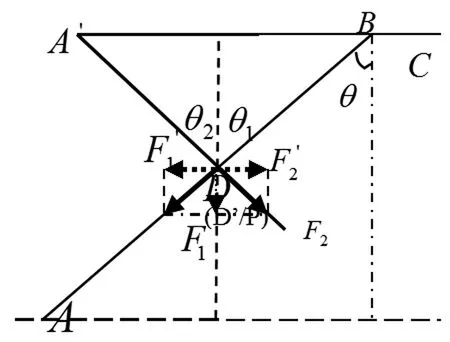
图2-1 受力分析图
又由力的合成与分解有:

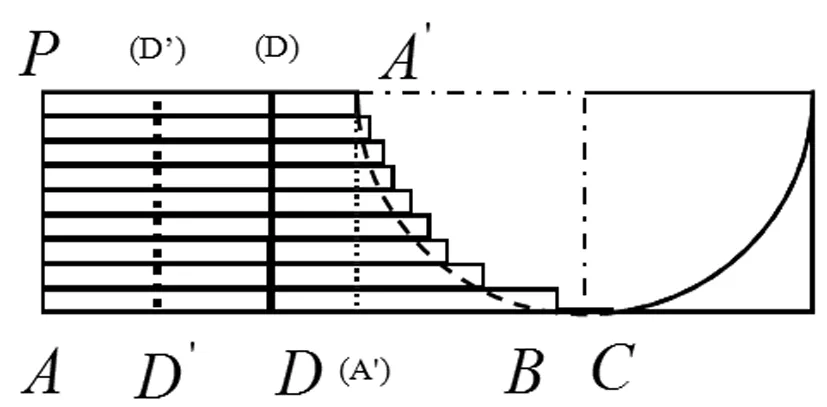
图2-2 折叠圆桌截取图
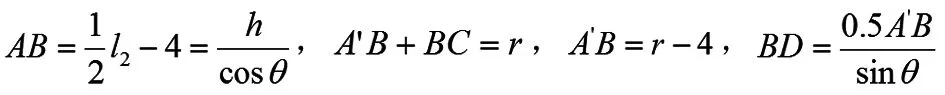
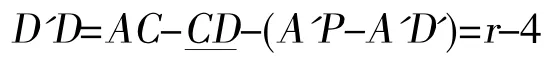
(2)物体的重心
结合物理学有关重心的知识,重心越低的物体,稳定性越高。本题中折叠桌的重心受桌子高度及槽长最大值的限制,不可能无限降低。要想重心达到可能范围内的最低点,需要使槽长尽可能长。由于槽长受到最短木条长度的限制,故槽长最大值为无限接近最短木条长度,即。但这是理想状态下,实际操作中求出的角度要略小。
要想稳定性达到最好,既要时受力平衡且左右分力较小,还要满足重心较低,故在理想情况下综合上述公式有:。
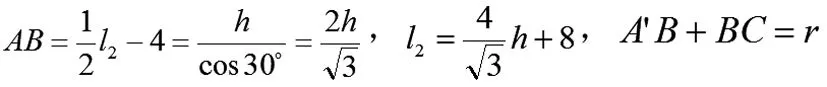
(3)给定数据代入模型求解
最后对于给出的桌面直径和折叠桌的高度,代入模型计算出折叠桌最稳定时:长方形平板长为cm,最短木条开槽长度为36cm,钢筋轴点到最外侧木条底端的距离与最外侧木条长度比为0.4454.
2、加工便利以及用材最少问题
加工便利和用材较少可以从平板被切割的条数的多少来研究。当切割的条数较少时,加工工序减少,用材耗用也减少。由于随着切割条数的减少,会使折叠桌的灵活性下降,但是要控制桌腿宽度与平板宽度的比例在一定的合理范围。
三、任意折叠桌设计
任意创意折叠桌设计,是本文的一次创新。想法的来源是对平面图形的分类,平面图形可分为由曲线和直线围城的平面,所以考虑任意桌缘形状是否可由曲线平面图和直线平面图大致拼接而成,因此我们设计了图形拼接模型。首先,根据问题一二分析已知曲线桌缘形状的折叠设计原理。其次,讨论直线桌缘形状折叠设计。最后,延伸到对任意桌缘形状的设计。
(一)折叠三角桌设计模型
1、模型的准备
针对由直线构成的桌缘形状进行折叠设计,将设计折叠三角桌,在一个三角形内分析如何设计折叠方式,对任意两条直线构成的角,在角内做圆,使圆与两直线相切,并且圆心位于该角的角平分线,沿相切点裁剪长方形木板,然后根据问题一二的参数设计,以及最优的稳定性状态,对木板沿直线边进行切割,最后,给出相应平板材料的形状尺寸和切实可行的最优设计参数,并描述动态变化过程。
2、模型的建立
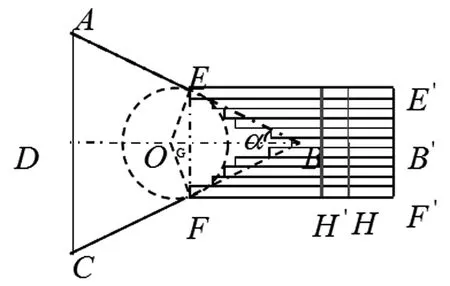
图3-1 三角形一角折叠设计原理图
在直角三角形中有,
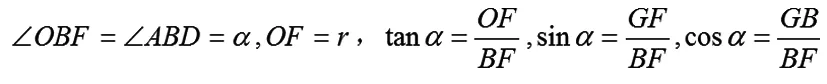
则有:
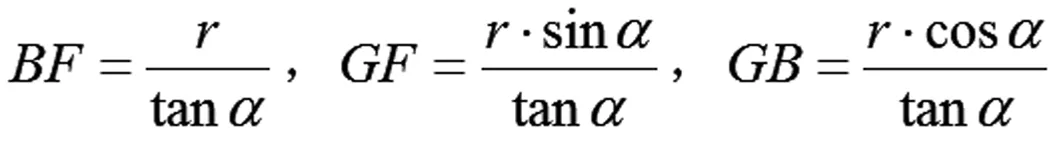
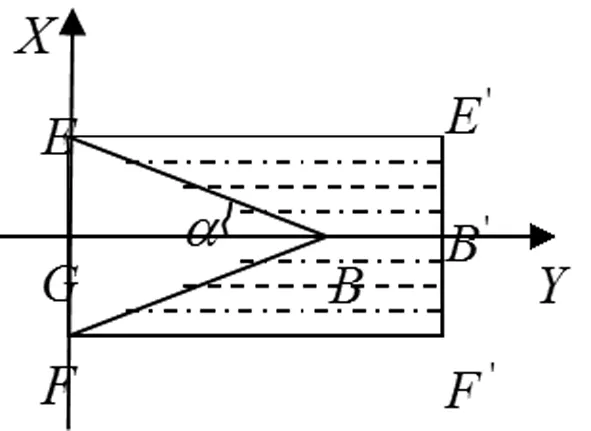
图3-2 平面示意图
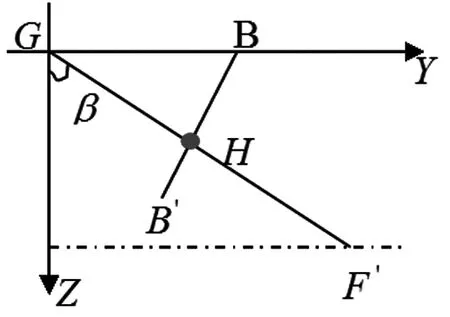
图3-3 平面示意图
结合图3-2和3-3,根据题目建立的直角坐标系,为了方便计算,本文取每个木条与桌边切线线段的中点为坐标点,且宽为的长形平板共分为条,故每一条木条的宽度为,则每个坐标点的横坐标(分别对应从最短木条到最长木条的横坐标)为:
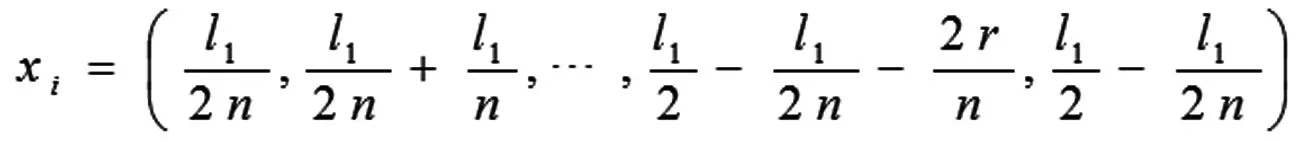
通过桌边方程,计算可得纵坐标为:
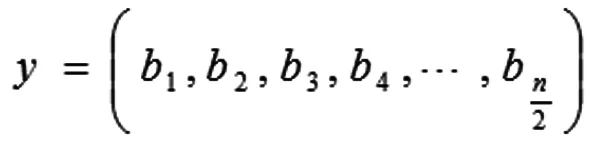
每一条桌腿的腿长:
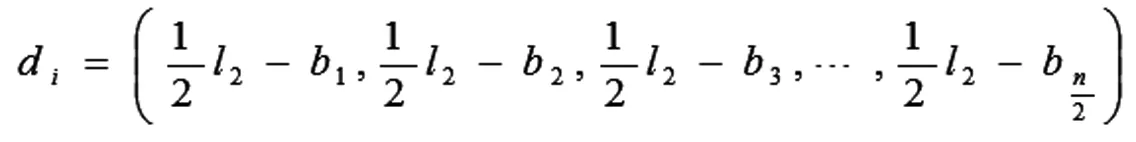
3、模型的求解
根据问题二槽长公式的推导过程,有:
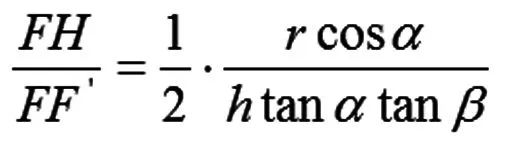
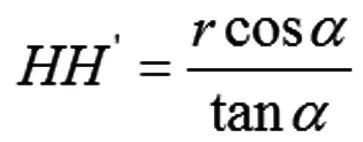
三角桌边折叠展开动态变化过程见下图3-4。
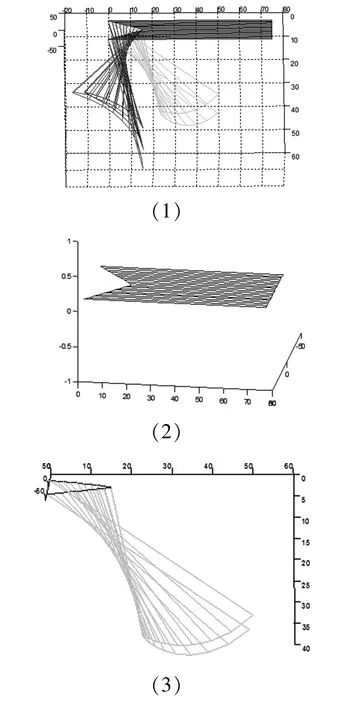
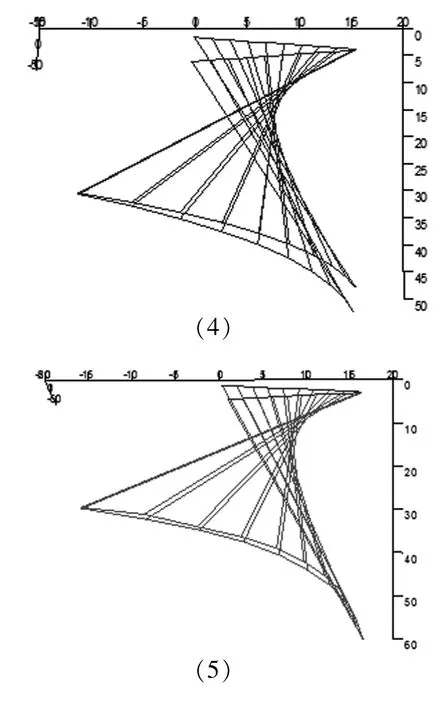
图3-4 三角桌边折叠展开动态变化过程示意图
(二)图形拼接模型——创意“蜜桃”折叠桌设计
1、模型的准备
结合上述问题分析,设计“蜜桃”平板折叠桌,首先,由于任意的桌缘边形大致可由直线边的平面和曲线边的平面拼接构成,对于“蜜桃”的桌缘边形,则可由菱形和半圆拼接而成,以知折叠桌高度,桌面边长及角度,可结合上述模型分析计算相应的设计参数。最后,针对任意桌脚边缘线问题,在合理的区域范围内针对顾客需求进行设计。
2、模型的建立与求解
(1)“蜜桃”桌缘边形的构成
本文设计的“蜜桃”桌缘边形大致由菱形和半圆拼接而成,如下图3-5所示。假设“蜜桃”折叠桌的高度为70cm,半圆和半径,菱形ABCD的各边边长为60cm,且∠ADC=120°。
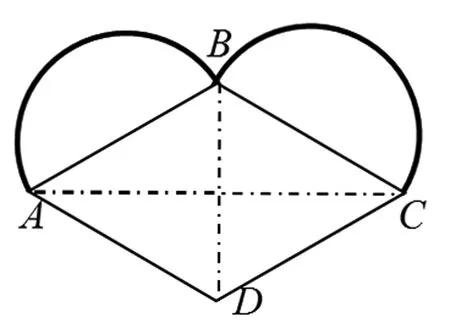
图3-5 “蜜桃”桌桌缘拼接图

图3-6 “蜜桃”折叠桌切割设计图
根据上述问题的相应参数求解过程,可求得该“蜜桃”折叠桌的相应设计参数值,如下表3-1。

表3-1 “蜜桃”折叠桌相应设计参数值
(2)任意桌脚边缘线的设计
对于任意桌脚边缘线的设计,在合理的区域范围内对桌腿木条进行剪裁以达到顾客的需求。针对区域范围的确定,将结合问题一对桌腿边缘线的求解,以折叠圆桌为例。结合图3-7和3-8,分析半圆桌桌腿边缘曲线和该曲线在x-y上的投影,可知该合理的区域为阴影面。
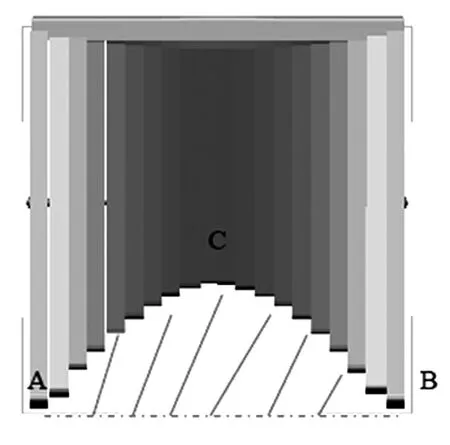
图3-7 半圆桌侧面实体图
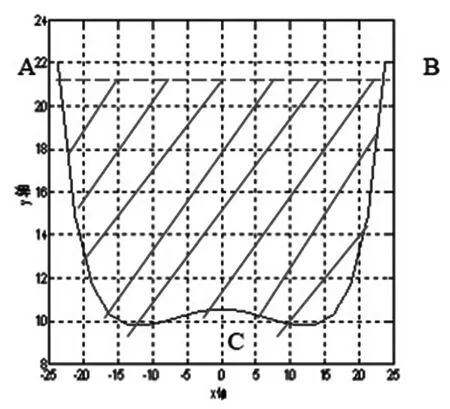
图3-8 桌腿边缘曲线x-y投影图
五、总结
作者还做了灵敏度分析,问题二中最终求的最优状态是开槽长度无限接近于最短桌腿长度,这是一种理想状态,实际中无法达到,即实际求得的角度要略小于。接下来讨论实际中角度略小的几种情况下设计参数的变化,计算结果如表5-1。
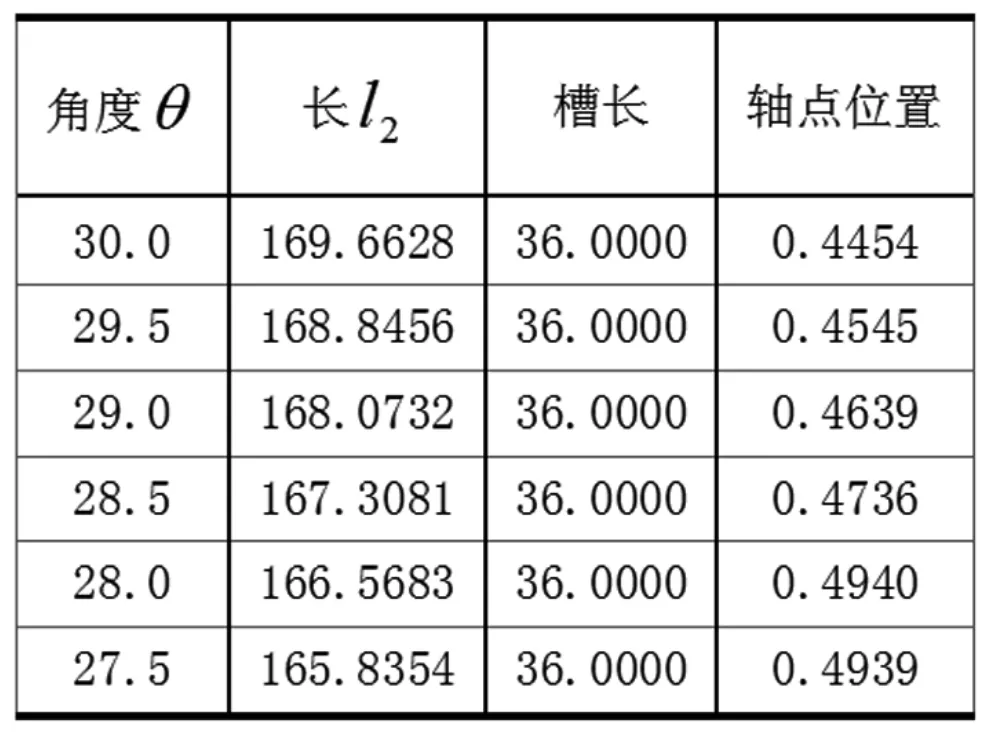
表5-1 不同角度下的设计参数
并且创新性提出图形拼接模型,可根据客户任意设定的折叠桌高度、桌面边缘线的形状大小和桌脚边缘线的大致形状,给出所需平板材料的形状尺寸和切实可行的最优设计加工参数,使得生产的折叠桌尽可能接近客户所期望的形状。
[1]杨桂元,黄己力.数学建模[M].合肥:中国科学技术大学出版社,2008.
[2]刘锡良,朱海涛.一种新型空间结构—折叠结构体系[J].工程力学,1996(03):497-500.
[3]颜卫亨,计飞翔,张茂功.折叠结构体系及类型[J].建筑科学与工程学报,2006.(04):70-73.
[4]吴礼斌.经济数学实验与建模[M].天津:天津大学出版社,2009.8.
[5]刘树青,吴金娇,汪木兰.基于有限元方法的剪式折叠结构力学特性分析[J].中国制造业信息化,2010,39 (15):51-53.
D18
A
1009-8534(2015)01-0069-05
2014-10-23
朱慧君(1996-),女,安徽东至人,安徽财经大学硕士。朱家明(1973-),男,安徽省泗县人,硕士,副教授,数学建模实验室主任,研究方向:应用数学与数学建模。
