基于四阶累积量的TAM算法电力系统谐波检测
2015-06-24余锦东徐明张春基程志友叶珊珊
余锦东,徐明,张春基,程志友,叶珊珊
(1、黄山市亿利工贸有限公司安徽·黄山242700;2、安徽大学电子信息工程学院安徽·合肥230601)
基于四阶累积量的TAM算法电力系统谐波检测
余锦东1,徐明1,张春基1,程志友2,叶珊珊2
(1、黄山市亿利工贸有限公司安徽·黄山242700;2、安徽大学电子信息工程学院安徽·合肥230601)
谐波检测是电力系统中无功补偿和谐波滤除等电能质量分析与控制的前提。本文结合四阶累积量和TAM算法,提出基于四阶累积量的TAM算法电力系统谐波检测。本文方法以信号空间为模型,首先用盖氏圆检测出信号源数,然后利用四阶累积量定义的矩阵代替传统二阶多信号分类法中的自相关矩阵做特征分解,将特征值对应的特征向量分为信号子空间和噪声子空间,再结合信号子空间和噪声子空间的正交性以及子空间的旋转不变性,估计出信号的频率。最后采用总体最小二乘法(TLS)计算得到信号的幅值。通过MATLAB软件仿真实验验证和实际电力系统数据分析表明该方法能有效地抑制高斯噪声,精确度高、抗噪性强,具有一定的应用价值。
四阶累积量 TAM 谐波检测
引言
随着经济的快速发展,电力电子产品爆炸式地应用于工业控制领域中,电能质量问题也越来得到人们的重视,其中最为突出的是谐波“污染”问题。因此,如何保证电压质量、降低电流谐波成为了输配电技术中亟待解决的问题[1]。
谐波抑制的首要关键问题是谐波电流的检测,它是进行无功补偿和抑制谐波等电能质量分析与控制问题的前提,因而,采用一种行之有效的谐波电流提取方法成了电力系统电能质量控制的第一步。当前,比较常用的几种检测方法,因为其基于的理论侧重点不同,因而或多或少会存在一些缺陷。如模拟带通滤波器的方法,它对硬件电路参数设计要求较高,虽实时性好,但是其检测的效果往往不如人意[2];基于瞬时无功功率理论的各类检测方法被广泛应用于各种场合,其检测精度高,实时性较好,但是对电网电压的锁相问题一直没有得到很好的解决[3];基于傅里叶变换理论的算法在每一周期里均需严格采样,其计算量比较大,实时性差[4]。基于小波变换的检测方法目前研究的比较多,但是小波变换仅仅是针对谐波信号的低频段进行了处理,其高频段的分辨精度较差,因此对于高次谐波的检测效果不是很好[5-6]。基于神经网络(Neural Network,NN)的方法[7]存在实时性好,分离精度高等优点,但是在实际运用中需用到很多的训练样本,其样本的确定目前并没有一种比较规范的方法。Pisarenko[8]的分离方法需要利用检测信号前面的一定先验知识,因此无法针对于实时的谐波信号进行有效的检测。
在实际的电力系统各类工况下,其噪声频谱分布是相当复杂的,而对于一个不具有高斯特征的噪声信号来讲,它的一阶、二阶等低阶累积量显然不能够很好地把信号的统计特性描述出来。研究表明[9-10][12-13],采用高阶累积量的形式不仅可以获得比二阶累积量更好的性能,而且能将二阶累积量不能描述费高斯信号的统计特性问题给解决了。本文结合盖氏圆方法、TAM(Toeplitz Approximation Method)算法及四阶累积量(Fourth-Order Cumulants,FOC)方法的优点,提出了一种基于FOC的TAM电力系统谐波检测方法(FOCTAM)。首先采用了盖氏圆方法来确定了一组阵列接收信号里面的谐波信号源的个数,然后用SVD的方法对四阶累积矩阵进行分解,由此得到了信号子空间和噪声子空间,由矩阵论可知,这两个子空间具有正交性和旋转不变性的特征,因此可以估计信号的频率,由总体最下二乘法[11]来确定各频率下的谐波幅值。由理论分析及仿真结果可以看出,本文所提出的方法估计精度比较高,实时性好,具体有一定的应用前景。
一、谐波检测原理
(一)信号模型
假设某周期信号x(t)以fs的采样频率进行采样后得到的形式如下式:

其中,s(n)是不含有噪声的原始信号,H为谐波的次数,υ(n)为所含有的高斯白噪声信号,fi为第i个正弦波信号的频率,Ai为第i个正弦波信号的幅值。
则接收信号模型的矩阵形式为
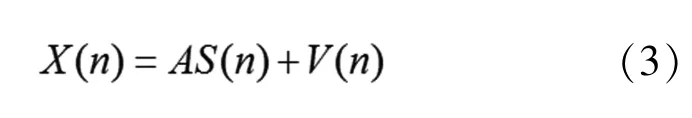
得到:
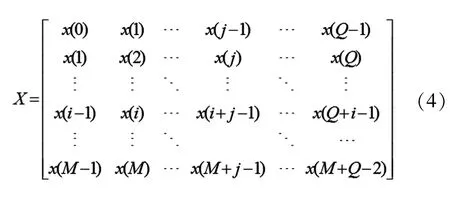
式中,M和Q的和为采样点的总数目。
(二)盖氏圆方法确定谐波源数目
当要采用四阶累积量TAM算法从某信号中分离出谐波分量时,能够准确判断出信号的谐波源数目是首先要解决的一个难点。而在实际的工业现场中,信号的谐波源数一般都是未知的,当所估计的谐波信号源数目和真实的谐波信号源数目不等时,前面所说的信号子空间和噪声子空间将不会完全地正交,从而导致真实信号的估计精度大大降低。在本文中,采用了盖氏圆的方法来估计出谐波信号源的数目这种方法一个显著的优点是它不需先验的知识,它采用盖氏圆盘定理判断出个特征值的位置,由此估计出谐波信号源的数目。
对一个M*Q维的X,我们设它第i行第j列的元素为rij,令其第i行元素的绝对值之和如下∶可定义第i个圆盘Oi上所有点可以利用在复平面上的集合(Z)用下式表示:
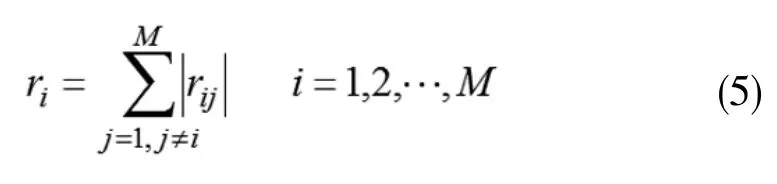

这个圆盘称之为盖氏圆盘。由盖氏定理可知,矩阵X的所有特征值均位于所有圆盘Oi的并区间内,每一个圆盘的圆心位于rii处,其半径为ri[12-13],这个半径被称为盖氏半径。对观察得到的信号的协防矩阵进行一次酉变换,这样能够使得信号的圆盘和噪声的圆盘分离出来,并且信号的圆盘的半径比较大,H个信号源所对应的特征值位于信号的圆盘覆盖的区域里,而噪声的圆盘的半径相对较小,个信号源所对应的特征值位于噪声的圆盘覆盖的区域里。利用数据协方差矩阵进行分块得到下式:
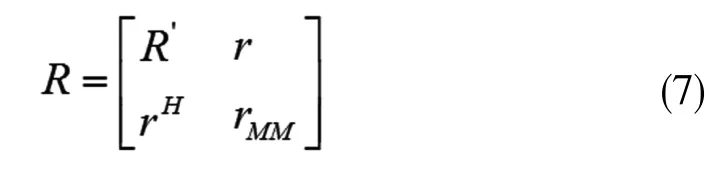
取M-1维方阵R’的特征空间重构酉变换矩阵T为:

酉变换之后的矩阵为:
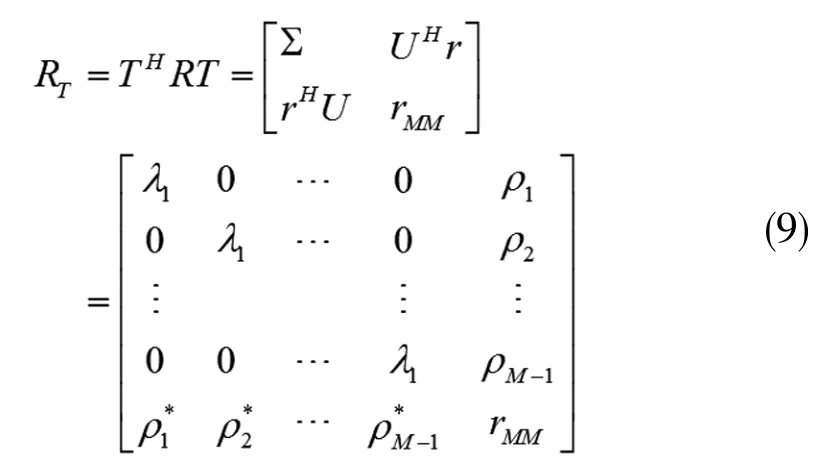

因此,盖氏圆的半径满足下式所示:
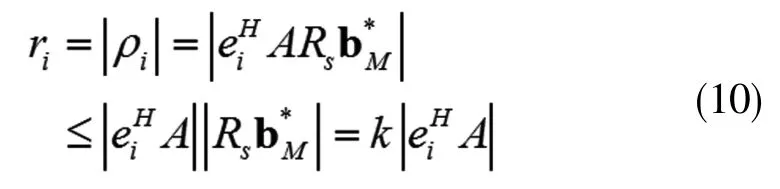
由此得到谐波信号源数目估计的式子如下:
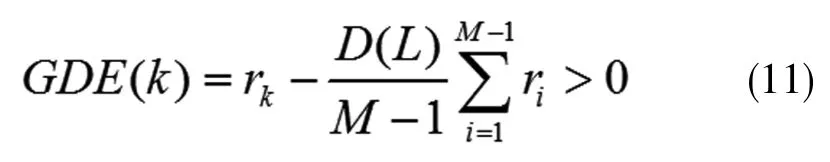
式中,D(L)为调制因子,它与快拍数有关,其一般的取值为0~1;k的取值范围为1~M-2。令k从小至大依次增大时,观察GDE(k)第一次出现负数的k为k0,可根据式H=k0-1来估计谐波信号源的数目。
(三)基于四阶累积量的TAM(FOC-TAM)算法
本文FOC-TAM算法利用了四阶累积量方法得到的四阶累积矩阵(R4)代替传统TAM算法中的协方差矩阵(R2)作特征值分解,然后从特征向量空间分离出信号子空间和噪声子空间,最后由向量空间正交性可以得到谐波信号源的功率谱及频率[14]。
对于零均值的信号源,阵列接收信号的协方差矩阵(R2)可表示为:

采用协方差矩阵来估计谐波信号源的方法的前提都是假定针对的对象是高斯信号,而其噪声为白噪声。在实际的工业现场中,一般不会这么理想,信号往往是非高斯的,加性噪声是有色的高斯过程,所以该方类方法只能取得次优的估计性能。由于非高斯的信号的四阶累积量往往含有大量的统计成分信息,所以采用四阶累积量矩阵的估计方法比协方差矩阵法有着不可比拟的优势。可设矩阵信号x(n)的四阶累积量如下式所示:

式中,cum{·}为随机过程的累积量;xki(i=1,2,...,4)为随机变量。
因为不同信号源具有相互的独立性,因此可将上式化简为:

式中:Ai(k)是第i个信号导向矢量的第k个元素,si(i=1,2,...H)为某一谐波信号源。γ4si为第i个信号的四阶累积量。
显然,四阶累积量cum{xk1,xk2,xk3,xk4}随着k1,k2,k3,k4的变化,共有M4个值。可以将四阶累积量的M4个值放入下面所定义的M2*M2矩阵R4[14]里面,得到:

其中:


对R4进行SVD分解可得:

频率参数的估计其中一个重要的环节便是信号子空间的划分。由得到的奇异值大小及其位置,可以将一个信号空间分别划分成信号子空间和噪声子空间。式(18)中,Σs表示由信号子空间的奇异值组成的对角阵,ΣN表示由噪声子空间的奇异值所组成的对角阵,不难看出,Σs的对角元素远大于ΣN的对角元素。
由旋转不变的定理可以由权矩阵Σs1/2重构一个新的矩阵D:

选择D1,D2为矩阵D的前L-1行与后L-1行。
则得到D1与D2的关系如下:

由(19)和(20)式得到下式:
上式中Us1为Us的前L-1行,Us2为Us的后L-1行。所以上式的最小二乘解为:
对矩阵F进行特征值的分解,便可得其旋转因子Φ,对角元素为φk,采样频率为fs,而谐波频率为:

由谐波信号的频率采用总体最小二乘的方法能够求出各个谐波频率下所对应的幅值。
二、仿真实验与结果分析
本文仿真实验所用的信号为:
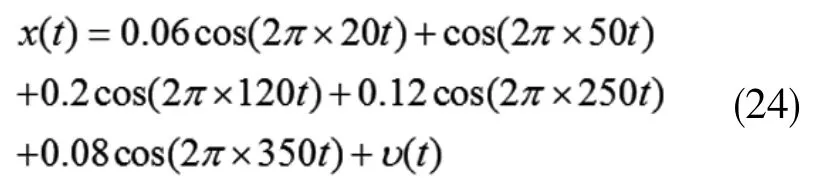
仿真中的采样频率为6400Hz。在仿真信号中,基波及5次和7次谐波频率相对应的幅值为0.12dB和0.08dB;20Hz的间谐波对应的幅值为0.06dB;120Hz的间谐波对应的幅值为0.20dB。为检验所提算法的鲁棒性,因此在仿真的信号里混入了信噪比SNR为30dB的高斯白噪声υ(t)。仿真信号0~0.1s的波形如图1所示。
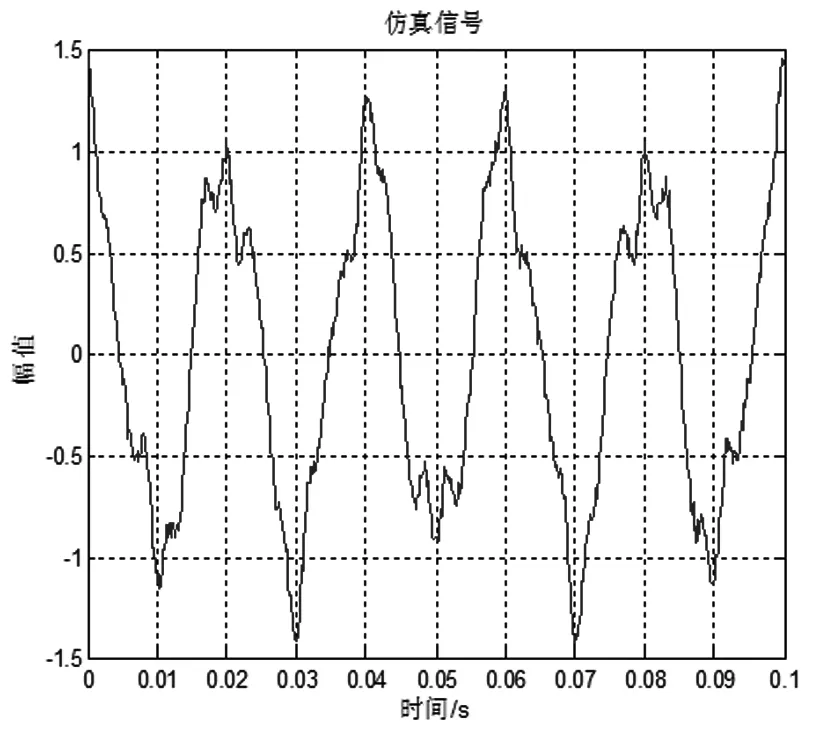
图1 仿真谐波信号波形图Fig.1 Waveform of the simulation signal
由盖氏圆的方法可以得出谐波信号源的数目是5,基于四阶累积量的TAM算法来分别提取出基波和各次谐波信号,得到的基波信号频率估计值为:50.0046Hz,幅值为0.9983;20Hz间谐波信号频率估计值为:20.0310Hz,幅值为0.0575;120Hz间谐波信号频率估计值为:120.2045Hz幅值为0.1873;250Hz谐波信号频率估计值为:249.9129Hz,幅值为0.1200;350Hz谐波信号频率估计值为:349.9791Hz,幅值为0.0695。仿真信号的频谱如图2所示。

图2 频率检测结果Fig.2 Frequencies estimated results
一般来说,总体相对误差能够反映出谐波检测的整体效果,因此本文利用总体相对误差来当做谐波检测效果评判标准。总体相对误差定义如下式:

式中,F(j)是仿真信号的频率(幅值)。F(j)’是经过算法分析得出的信号的频率(幅度的平均值),是各谐波的次数。
由于基于四阶累积量的ESPRIT算法具有不受阵列集合形状的限制的优点,因此其较传统的ESPRIT算法对模型误差这个指标具有鲁棒性[15]。为了能更进一步地验证所提算法的精确性,选用了如式(24)所示的仿真信号,将所提出的算法与文献[16]中基于四阶累积量的ESPRIT算法及基于四阶累积量的MUSIC算法进行比较,由此得到参数估计值及其相应的相对误差仿真结果如表1所示:
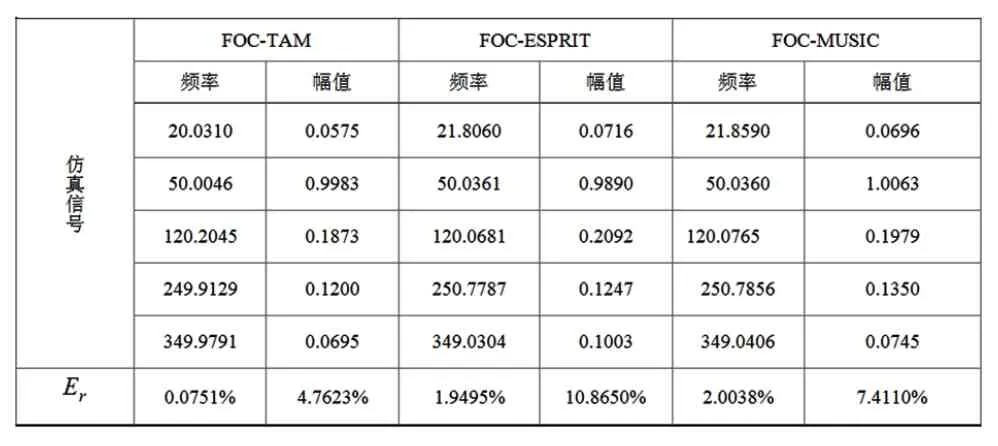
表1 本文算法和FOC-ESPRIT及FOC-MUSIC算法比较Tab.1 Comparison between the algorithm both FOC-ESPRIT and FOC-MUSIC
由表1可知,采用FOC-ESPRIT算法分析得到频率和幅值的总体相对误差分别为1.9495%和10.8650%;而FOC-TAM算法分析得到的频率和幅值的总体相对误差分别为0.0751%和4.7623%。再分别对比FOC-TAM算法与基于四阶累积量的MUSIC(FOC-MUSIC)算法,分别计算频率、幅值相对误差。以基波信号和20Hz的间谐波信号为例,基波信号FOC-TAM分析以后的估计结果是50.0046Hz,幅值为0.9983。FOC-MUSIC分析以后的估计结果是50.0360Hz,幅值为1.0063;而20Hz的间谐波信号分析以后的估计结果是20.0310Hz,幅值为0.0575。FOC-MUSIC分析以后的估计结果是21.8590Hz,幅值为0.0696。因此可知,FOC-TAM算法比传统的FOC-ESPRIT算法和FOC-MUSIC算法分析得到的结果更精确,误差更小。
分别设置不同的信噪比,采用以上三种算法对如式(24)所示的仿真信号来估计频率和幅值。图3和图4分别为频率误差、幅值误差与信噪比关系。由此可知,在不同的信噪比环境下,FOC-TAM,FOCESPRIT,FOC-MUSIC算法的分析出来的频率估计值相差不大,且随着信噪比降低,估计精度也随之下降,当SNR=15dB时,误差值为19.3383%。在使用FOC-TAM算法估计的幅值误差下,当信噪比较高时,FOC-ESPRIT算法估计结果是明显优于FOCMUSIC算法的。因此可以验证,FOC-TAM算法比FOC-ESPRIT、FOC-MUSIC算法有更好的抗干扰性,即使是在低噪声比的环境下FOC-TAM算法也能够较准确地估计出频率与幅值。

图3 频率误差Fig.3Frequencyerror
三、实时数据检测与结果分析
为了更进一步地验证所提出的算法在工业现场的可行性和优越性,提取某炼钢的电弧炉的A相电压数据,并采用FOC-TAM算法对所得到A相电压采样数据进行分析。图5为该炼钢厂电弧炉在1~1.2s时间范围内三相电压波形图,其采样频率为6400Hz。图6为通过FOC-TAM算法进行分析得到的A相电压频率检测结果。
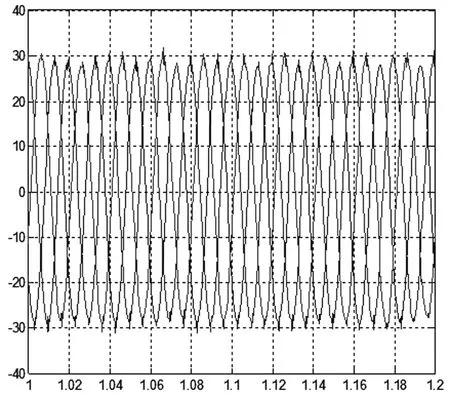
图5 实时信号波形图Fig.5Waveformofreal-timesignal

图6 FOC-TAM算法检测的频率检测结果Fig.6 Frequencies estimated results via FOC-TAM
由图6可以看出,A相电压波形有畸变,其波形信号含有丰富的高次谐波和间谐波。经过FOC-TAM算法将基波和幅值较大的各次谐波间谐波信号提取出来,可得:基波的频率为50.0030Hz,其幅值为0.3799。其他的谐波频率大小分别为:6.2874Hz,25.1299Hz,,72.5963Hz,92.2864Hz,108.3867Hz,143.3322Hz,249.7722Hz,299.3657Hz,349.4679Hz。对应的幅值(kA)分别为:0.1662,0.0170,0.06526,0.7577,0.0296,0.0179,0.026 0,0.0260,0.0110。实验结果表明该算法在实时数据处理上,具有一定的可应用性。
四、结论
本文将四阶累积量与TAM算法有机结合起来,形成一种新型的检测方法,并将该方法应用于电力系统的谐波检测。首先,本文用盖氏圆的方法估计出信号源数使该算法具有实用性,然后结合本文所提的算法来分析电力系统谐波,由此能较准确地计算出包含谐波、间谐波的幅值和频率等相关参数。仿真及实验表明,本文所提出的算法在相同的信噪比环境下,其检测效果均优于FOC-ESPRIT和FOCMUSIC,精确性更高,抗噪声性强,可应用于实时谐波信号的检测和分析。由此验证本文所提出的算法的正确有效性,可以为谐波、间谐波的分析提供一种新的工具。
[1]电网谐波治理和无功补偿技术及装备[M].北京:中国电力出版社,2004.
[2]Vlahinic,Dalibor,Dubravko.Measurementand analysis of harmonic distortion in power distribution systems[J].Electric Power Systems Research,2009,79(7): 1121-1126.
[3]梁志瑞,叶慧强,赵飞.电力系统谐波状态估计研究综述[J].电力系统保护与控制,2010,38(15):157-160.Liang Zhi-rui,Ye Hui-qiang,Zhao Fei.Overview on power system harmonic state estimation[J].Power System Protection and Control,2010,38(15):157-160.
[4]Sanoso S,Grady W M,Power E J,et al.Characterization of distributes power quality events with Fourier and wavelet transforms[J].IEEE Transaction on Power Delivery,2000,15(1):247-254.
[5]龚华麟,肖先勇.非线性度法在配电网谐波源探测中的应用[J].电力系统保护与控制,2010,38(8):30-34. Gong Hua-lin,Xiao Xian-yong.Application of nonlinearity degree method in harmonic source detecting in distribution network[J].Power System Protection and Control,2010,38(15):30-34.
[6]周林,夏雪,万蕴杰,等.基于小波变换的别波测量方法综述[J].电工技术学报,2006,21(9):67-73. ZhouLin,XiaXue,WanYun-jie,etal.Harmonic Detection Based on Wavelet Transform[J].Transactions of CHINAElectroTechnicalSociety,2006,21(9):67-73.
[7]张海燕.VSC-HVDC输电系统的模糊神经网络控制[J].电测与仪表,2010,47(07):34-41. Zhang Hai-yan.Fuzzy Neural Networks Controller for VSC-HVDCTransmissionsystem[J].Electrical Measurement&Instrumentation,2010,47(07):34-41.
[8]王志群,朱守真,周双喜,等.基于Pisarenko谐波分解的间谐波估算方法[J].电网技术,2004,28(15):2-77,82 Wang Zhi-qun,Zhou Shuang-xi,et al.Interharmonic estimationbyPisarenkoharmonicdecomposition method[J].Power System Technology,2004,28(15):72-77,82.
[9]Shi Z,Fairman F W.DOA estimation via higherorder cumulants:a generalized approach.1992 ICASSP,5, 209~212.
[10]Papadopoulos C K,Nikias C L.Parameter estimation of exponentially damped sinusoids using higher order statistics.IEEE Trans.on ASSP,1998,38(8):1424~1436.
[11]张滨生,喻乐,和敬涵,周文.基于快速TLSESPRIT的间谐波检测算法[J].电力自动化设备, 2011,31(2):26-31. Zhang Bing-sheng,Yu Le,He Jing-han,Zhou Wen. Inter-harmonic detection based on fast TLS-ESPRIT[J]. Electric Power Automation Equipment,2011,31(2):26-31.
[12]Wu H T,Yang J F,Chen F K.Source number estimatorusinggerschgorindisks[J].ProICASSP, Adelaide,Australia,1994,261-264.
[13]Wu H T,Yang J F,Chen F K.Source number estimator using transformed gerschgorin radii[J].IEEE Trans.on SignalProcessing,1995,43(6):1325-1333.
[14]王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社,2004. Wang Yong-liang,Chen Hui,Peng Ying-ning,et al.The theory and algorithms on the spatial spectrum estimation [M].Beijing:the press of QingHua University,2004
[15]唐建红,司锡才,彭巧乐.快速四阶累积量旋转不变子空间算法[J].西安交通大学学报,2009,43(6):88-92. Tang Jian-hong,Si Xi-cai,Peng Qiao-le.Estimation of signal parameters via rotational invariance techniques algorithm with speedy fourth-order cumulants[J].Journal of Xi'an Jiaotong University,2009,43(6):88-92.
[16]Roy R,Kailath T.ESPRIT-estimation of signal parameters via rotational invariance techniques.IEEE Trans.1989,37(7):984-995
TM12
A
1009-8534(2015)01-0061-06
2014-09-15
余锦东,黄山市亿利工贸有限公司职工。
