基于双曲正切函数的变步长凸组合最小均方误差算法

陈立伟， 谭志良， 崔立东

(军械工程学院静电与电磁防护研究所， 河北 石家庄 050003)

基于双曲正切函数的变步长凸组合最小均方误差算法

陈立伟， 谭志良， 崔立东

(军械工程学院静电与电磁防护研究所， 河北 石家庄 050003)

利用双曲正切函数对凸组合最小均方(Convex Combination of Least Mean Square, CLMS) 算法进行了改进，提出了Th-VSCLMS(Tanh Variable Step Convex Combined Least Mean Square)算法。理论分析表明：改进算法的性能优于普通的变步长算法。在不同信噪比下对VSLMS(Variable Step Least Mean Square)、CLMS、Th-VSCLMS算法进行了仿真对比分析，结果表明：Th-VSCLMS算法的收敛性、稳态性、抗扰动性、低信噪比的滤波效果、计算量均得到较好的改善，且其凸组合滤波结构优于单一滤波结构。

凸组合最小均方算法；双曲正切函数；拟合系数

最小均方(Least Mean Square，LMS)算法由Widrow和Hoff提出[1]，其收敛速度与步长成正比，稳态误差与步长成反比[2]。现有固定步长的LMS算法很难同时获得初始收敛速度与稳态误差均良好的性能，为解决二者的矛盾，许多变步长算法先后被提出，其中最具代表性的算法有：归一化最小均方(Normalized Least Mean Square,NLMS)算法[3]、改进的Sigmoid函数变步长LMS(Sigmoid Variable Step-size of Least Mean Square,SVSLMS)算法[4]、指数因子变步长LMS算法[5]等。变步长LMS算法虽然通过对算法步长的折中，使收敛速度和稳态误差基本都能满足实际应用的要求，但其对2种性能都有限制，因而也抑制了自适应滤波器处理信号的性能。

近几年，利用并行计算思想提出了凸组合最小均方(Convex Combination of Least Mean Square,CLMS)滤波器算法[6]。该算法将2个不同迭代步长的最小均方算法滤波器并联起来，其中：一个滤波器提高算法的收敛速度；另一个滤波器保证稳态性能。于霞等[7]提出了一种变步长凸组合最小均方(Variable Step-size Convex Combination of Least Mean Square,VSCLMS)滤波器算法，其利用变步长调整原则，将其中1个固定步长LMS算法滤波器改为变步长LMS(Variable Step-size of Least Mean Square, VSLMS)算法滤波器，该滤波器在收敛速度、跟踪性能、系统失调性等方面都有较大提高。本文利用双曲正切函数(Hyperbolic Tangen Function，Tanh)，作为其中快速LMS算法的步长函数来提高算法的收敛速度与稳态性，提出了Th-VSCLMS算法并通过仿真分析验证其性能。

1 VSCLMS算法

VACLMS算法滤波器原理[6]如图1所示。其中：wi(n)、yi(n)、ei(n)(i=1,2)分别为LMS滤波器的权重、输出和误差；λ(n)、yeq(n)、eeq(n)分别为VSCLMS滤波器的联合系数、输出和误差；u(n)为输入；d(n)为期望输入。

图1 VSCLMS算法滤波器的原理

变步长凸组合自适应滤波器克服了单一滤波器存在的不足，其采用2套完整的滤波器对信号进行处理，通过1个联合系数λ(n)来控制2个滤波器在整个滤波过程发挥作用的比例，使其在提高收敛速度或降低稳态误差时不降低另一方面的性能。

VSCLMS算法滤波器的等价权向量为

w(n)=λ(n)w1(n)+[1-λ(n)]w2(n)，

(1)

式中：λ(n)∈[0,1],

λ(n)=sgm[a(n)]=1/(1+e-a(n)),

(2)

其中，

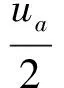
a(n-1)+uaeeq(n-1)[e2(n-1)-e1(n-1)]×

λ(n-1)[1-λ(n-1)],

(3)

为以最小均方误差为准则进行自适应的函数，符合LMS理论的鲁棒性[7]。式(3)中,ua为综合步长。

输出为

yeq(n)=λ(n)y1(n)+[1-λ(n)]y2(n)。

(4)

误差为

eeq(n)=λ(n)e1(n)+[1-λ(n)]e2(n)=

λ(n)[d(n)-w1(n)uT(n)]+

[1-λ(n)][d(n)-w2(n)uT(n)]=

d(n)-w(n)uT(n),

(5)

式中:

ei(n)=d(n)-wi(n)uT(n),i=1,2。

(6)

由算法的结构与原理可得：在收敛初始阶段，应利用较大步长的VSLMS滤波器(λ≈1，weq≈w1)；收敛到稳定阶段时，则利用较小步长的VSLMS滤波器，以确保误差更小(λ≈0，weq≈w2)。

2 Th-VSCLMS算法分析

2.1 凸组合滤波器结构的优越性

通常采用额外均方误差(Excess Mean Square Error, EMSE)来衡量滤波器的性能，并将其定义为滤波器在工作过程中除最小均方误差外的额外误差项。为便于分析凸组合算法优于其中任何单独的LMS算法，假设学习迭代次数n取其极限值∞，由于e(n)=ea(n)+e0(n),其中:ea(n)为先验误差;e0(n)为独立建模观测噪声[8]。则根据EMSE计算公式

(7)

(8)

可得各滤波器的EMSE。

定义基于ea(n)的综合EMSE为

(9)

由式(9)与Cauchy-Schwartz不等式可得：滤波器的综合EMSE不会同时高于单个滤波器的EMSE，即

Jex，1,2(∞)≤max{Jex，1(∞),Jex，2(∞)}。

(10)

由上述分析可知：凸组合自适应滤波器的EMSE优于组合中任何单一自适应滤波器的EMSE。

2.2 TH-VSCLMS算法

本文提出以Tanh为变步长自适应滤波器的步长因子，另一个为固定步长的自适应滤波器。TH-VSCLMS算法可表示为

u(n)=βtanh(α|e(n)|γ),

(11)

式中：β为控制步长函数的范围；α为控制步长函数的形状；γ为控制步长函数在误差接近0时底端的平滑程度。

图2为tanh函数与Sigmoid函数的拟合曲线。Sigmoid函数是变步长LMS算法中步长函数的标准，大部分变步长函数均基于此函数得来。

图2 tanh函数与Sigmoid函数的拟合曲线

由图2可知：tanh函数符合变步长函数的变化准则，即步长随误差的变化而变化。在收敛的初始阶段，滤波器要求较快的收敛性能，此时可将β设置为允许范围内的最大值(β≤1/λmax)；在收敛稳态阶段，步长逐渐变小，保证了较小的稳态误差，但在稳态阶段，由于被污染的噪声容易造成步长的波动，使算法的稳态性能下降，可利用CLMS滤波器的另一个固定步长的LMS算法来减小稳态性能的损失。

2.3 复杂度分析

从公式的复杂度分析可看出：与CLMS算法、VSLMS算法相比，Th-VSCLMS算法的计算量有相应增加，特别是与传统的VSLMS算法相比，增加更多；较大的计算量对其硬件实现提出了更高要求。但综合分析来看：Th-VSCLMS算法收敛速度较快，从而减小了算法的计算量，且快速的收敛性在许多情况下非常重要，如军用雷达需要在较短的时间内发现和跟踪目标；另外，该算法的凸组合结构有较好的抗干扰能力，能更好地保证通信信号的质量。

3 仿真分析

将Th-VSCLMS算法、CLMS算法、VSLMS算法用于干扰抵消仿真中，进一步验证Th-VSCLMS算法的性能。通过200次独立仿真并求其平均值。为了客观对比3种算法的收敛性与跟踪性能，设Th-VSCLMS算法的参数值为：β=3，α=500，u2=0.01,ua=20。CLMS算法、VSLMS算法的参数取值引用文献[6]中的参数值：VSLMS算法中，α=300,β=0.05；CLMS算法中，u1=0.1,u2=0.05,ua=20。

3.1 抗干扰性能仿真

设滤波器阶数为8；期望信号为正弦信号S(s=sin(0.01πt))与高斯白噪声U(均值为0，方差为0.1)的叠加；参考输入信号为与U成比例函数的高斯白噪声V,设相应信噪比SNR=10。为了更好地比较算法的跟踪性能，设迭代到1 500次时权值突变，得出如图3所示的收敛曲线。

图3 3种算法的收敛曲线比较

由图3可见：1)在第1次收敛时，Th-VSCLMS算法迭代到250次时即进入稳态收敛阶段，其他2种算法迭代到420次后才进入稳态收敛阶段，可见在初始收敛阶段，Th-VSCLMS算法以较少的迭代次数进入稳态，计算量较小，稳态误差最小，表明Th-VSCLMS算法无论在收敛速度还是在稳态误差方面都表现突出，CLMS算法与VSLMS算法收敛性与稳态性差别不大；2)在第2次收敛时，Th-VSCLMS算法的收敛速度更快，表明Th-VSCLMS算法的抗干扰性能最好，而CLMS算法与VSLMS算法相比，CLMS算法的收敛速度也有明显改善，表明凸组合结构较单一滤波器优越。

3.2 低信噪比下的性能仿真

比较3种算法在低信噪比下的性能，设高斯白噪声U的均值为0，方差为1，相应信噪比SNR=0。各算法的收敛曲线对比如图4所示。

图4 低信噪比下3种算法的收敛曲线

由图4可以看出：在低信噪比下，Th-VSCLMS算法仍具有良好的性能。

3.3 结果分析

1) 虽然Th-VSCLMS算法比CLMS算法、VSLMS算法要复杂很多，但其在收敛阶段的计算量小，其迭代次数仅为CLMS算法、VSLMS算法的3/5左右，因此较少的迭代次数使三者的计算量相差不大，走出了因其较高复杂度必然带来更大计算量的误区。

2) 凸组合结构的抗干扰能力较好。CLMS算法与VSLMS算法在第1次收敛时速度相同，但当权值突变后CLMS算法的收敛速度明显快于VSLMS算法，表明凸组合结构较优越。

3) 低信噪比下Th-VSCLMS算法在收敛性能和稳态性能方面依然优于其他2种算法。

4 结论

本文基于双曲正切函数改进了CLMS算法，提出了Th-VSCLMS算法，通过理论与仿真对比分析验证了该算法性能的优越性。但论文只是从理论与仿真层面验证了算法，算法的参数选择虽然基于大量的仿真数据和前人的结论，但不乏会出现误差，下一步将基于这2方面的问题对算法进行深入研究。

[1] 张立峰,张树群,雷兆宜，等.基于梯度向量的变步长LMS算法[J].科学技术与工程,2013,13(25):7538-7541.

[2] 吕春英,敖伟,张洪，等.一种新的变步长LMS算法[J].通信技术,2011,44(3):11-14.

[3] 曾召华,刘贵忠,赵建，等.LMS和归一化LMS算法收敛门限与步长的确定[J].电子与信息学报,2003,25(11):1469-1474.

[4] 高鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报,2001,29(8):1094-1097.

[5] 杨逸，曹祥玉，杨群，等.基于指数函数的归一化变步长LMS算法[J].计算机工程，2012，38(10):134-136.

[6] Arenas-Garcia J,Figueiras-Vidal A R.Steady-state Performance of Convex Combinations of Adaptive Filters[J].IEEE Signal Pressing,2005,4(4):33-36.

[7] 于霞,刘建昌,李鸿，等.一种变步长凸组合自适应滤波器及其均方性能分析[J].电子学报,2010,38(2):480-484.

[8] 苗俊，芮国胜，张洋，等.变步长凸组合LMS自适应滤波算法及分析[J].应用科学学报,2013,31(5):475-480.

(责任编辑: 王生凤)

A Convex Combination of Variable Step LMS Algorithm Based on Hyperbolic Tangent Function

CHEN Li-wei, TAN Zhi-liang, CUI Li-dong

(Institute of Electrostatic and Electromagnetic Protection, Ordnance Engineering College, Shijiazhuang 050003,China)

The Convex Combination Least Mean Square(CLMS) algorithm is improved by means of hyperbolic tangent function and the Tanh Variable Step Convex Combination Least Mean Square (Th-VSCLMS) algorithm is proposed accordingly. Theoretically, the improved algorithm is superior to conventional variable step algorithm, and VSLMS, CLMS and Th-VSCLMS algorithm are compared and analyzed at different SNR. Simulation results show that Th-VSCLMS is well improved at convergence, steady, anti-disturbance, filtering effect in the low SNR as well as computation, and the convex combination have better filter structure than a single filter structure.

Convex Combined Least Mean Square algorithm; hyperbolic tangent function; fit factor

1672-1497(2015)05-0094-03

2015-05-13

国防科技重点实验室基金资助项目(9140C87030413JB34001)

陈立伟(1990-)，男，硕士研究生。

TN713

A

10.3969/j.issn.1672-1497.2015.05.019