多轮独立驱动装甲车辆稳定性控制

张运银， 马晓军， 刘春光， 廖自力， 张同振

(1. 装甲兵工程学院控制工程系， 北京100072; 2. 石家庄机械化步兵学院训练部， 河北 石家庄 050083)

多轮独立驱动装甲车辆稳定性控制

张运银1， 马晓军1， 刘春光1， 廖自力1， 张同振2

(1. 装甲兵工程学院控制工程系， 北京100072; 2. 石家庄机械化步兵学院训练部， 河北 石家庄 050083)

为实现多轮独立驱动装甲车辆行驶稳定性控制，提出了1种基于G向量控制的驱动力控制方法，利用车辆的横向加速度信息对车辆的总驱动力矩进行了修正。基于2自由度车辆模型，从负载转移和纵向驱动力影响的角度分析了该稳定性控制方法的理论依据。基于人在环实时仿真系统进行了8×8轮毂电机驱动装甲车辆实时仿真实验，对该稳定性控制算法进行了验证，仿真结果表明：该控制方法能够有效增强对车辆横向运动的控制能力，提高车辆行驶稳定性。

电传动； 多轮独立驱动； G向量控制；实时仿真

与传统机械传动车辆集中式驱动相比，基于轮毂电机驱动的多轮独立驱动具有独特优势，各驱动电机的扭矩可以独立、精确地控制，为整车稳定性控制带来更多自由度。目前，对多轮独立驱动控制的研究主要集中在4轮独立驱动车辆，一般以横摆转矩控制为基础，根据各驱动轮状态[1-4]或车辆状态[5]，控制各驱动电机的输出，进而实现对整车稳定性控制。其控制特点是强调对单个驱动轮纵向驱动力的优化控制，缺乏对总体驱动能力的调节。文献[6-7]作者则忽略单个驱动轮控制的影响，基于双侧纵向驱动力控制的思想，提出了一种双重转向的控制策略，即在理论计算的横摆转矩需求基础上再增加适量横摆转矩，用于转向的转矩输出,仿真结果表明：双重转向控制减小了车辆在中、低速转向时的转向半径，能够提高车辆的转向性能。但此方法仅限于转向控制过程，并且过大的转向扭矩负载易使车辆底盘发生机械故障。国内关于8轮独立驱动控制车辆的研究极少，只有部分类似方案的简单动力学仿真[8]。

笔者以8×8轮毂电机驱动装甲车辆为研究对象，提出了一种基于G向量控制的顶层驱动力控制方法，利用车辆的横向加速度信息对车辆的总驱动力矩进行修正，进而实现对整车的稳定性控制，并基于人在环实时仿真系统进行实时仿真试验，对该稳定性控制算法进行验证。

1 G向量控制

G向量控制基本规则可以表示为[9-11]

(1)

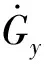
G向量控制规则可由图1形象表示:当车辆开始转向时，车辆整体纵向速度减小，驱动性能适当降低；当达到稳定转向时，横向加加速度为0，车辆速度趋于恒定；当车辆转向轮回正时，车辆开始加速，车辆纵向加速性能恢复；当车辆转向轮完全回正时，横向加加速度为0，车辆速度恢复到转向前的状态。

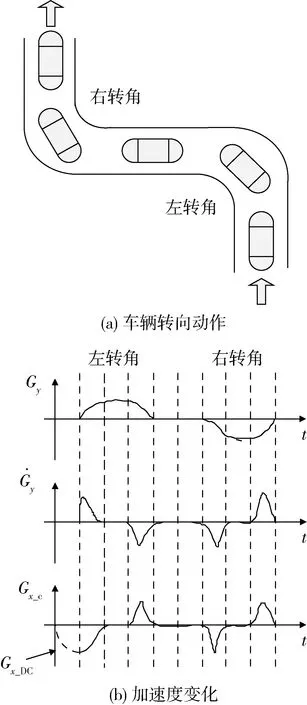
图1 G向量控制规则

根据车辆油门踏板信号解算出基本的总需求驱动力矩Tref为[12]

(2)

式中：κ为油门开度，κ∈[0,1]；ni为电机i(i=1,2,…,8)的当前转速；Tmax(ni)为电机i在当前转速下的最大输出转矩。

采用PI控制器计算车辆总需求驱动力矩修正量ΔT为

(3)

式中：Gx为纵向加速度；kp1和ki1分别为比例与积分系数。则最终车辆总需求驱动力矩T为

T=Tref+ΔT。

(4)

2 G向量控制可行性分析

忽略车辆的侧倾运动和俯仰运动，则车辆的运动可看作是刚体作平面运动。车辆平面运动方程可表示为[13-14]

(5)

式中：m为车辆质量；γ为横摆角速度；Iz为绕车辆垂向的转动惯量；Xf、Xr分别为前、后轮纵向牵引力；Yf、Yr分别为前、后轮横向力；lf、lr分别为车辆前、后轴到质心的距离。

2.1 负载相关性分析

轮胎侧偏刚度Kq与垂直载荷Wq关系可近似表示为

Kq=CWq,

(6)

式中：C为系数；q分别代表前(f)、后(r)轮。

考虑加速度影响下的载荷转移，前、后轮载荷Wf和Wr分别为

(7)

式中：g为重力加速度；l为前后轴距离；h为质心高度。

因此，前、后轮侧偏刚度Kf和Kr分别为

(8)

式中：Kf0、Kr0分别为前、后轮稳态侧偏刚度。

则前、后车轮的横向力Yf和Yr分别为

(9)

式中：Yf0、Yr0分别为前、后轮稳态横向力；αf、αr分别为前、后轮侧偏角。

从2个角度对式(9)进行分析：1)Yf和Yr恒定时，根据Gx来控制αf和αr，其与主动4轮转向的工作原理相类似，即欲增大Gx，需增大αf且减小αr；2)当αf和αr一定时，Yf和Yr直接受Gx控制。

将式(9)代入式(5)中进一步整理可得

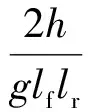
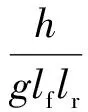
(10)

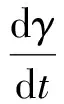
(11)

式中：Gy0、M0分别为稳态时的横向力和横摆转矩。

采用G向量控制，转向时，车辆减速，Gx<0；当转向稳定时，Gx=0；转向回正时，车辆加速，Gx>0。因此，在车辆减速过程中，车辆的横向运动和横摆运动被加强，操控性能得以提高；当转向达到稳定时，转向操控性能回归正常水平；在转向轮完全回正、车辆直线行驶时，横向力和横摆运动减弱，车辆保持直线运动方向的能力增强。

2.2 纵向牵引力相关性分析

总的纵向牵引力X可近似表示为

X=mGx，

(12)

前、后轮纵向牵引力Xf、Xr分别为

(13)

式中：η为比例系数，且η∈[0,1]。

假定轮胎与地面之间的摩擦因数为μ，则轮胎与地面的摩擦力Fj为

Fj=μWj。

(14)

由摩擦圆理论[15-16]可知：轮胎纵向力Xj与横向力Yj的关系为

(15)

因此，可以通过Xj来修正式(9)计算所得的Yj(在2.1节中，没有考虑纵向牵引力的上限问题)。修正值Yj-X可表示为

(16)

对式(16)中的平方根取适当的估值，则式(9)可进一步表示为

(17)

实际上，按照一般的车辆参数进行计算，式(17)的方括号部分将一直为正且小于1，无论Gx取何值(Gx≠0)，与式(9)相比，Yf和Yr都处于减小趋势。因此，Xf和Xr变化会导致Yf和Yr减小，具体表现为:因Xf和Xr增大或减小而使Gx为正或负时，Yf和Yr都会减小;减少量直接受Gx变化量控制,特别是μ较小时，Yf和Yr的变化幅度将明显增大。

由上述分析可知，由Gx变化引起的Yj的改变表现在2个方面：1)垂向负载转移引起的横向力增强；2)纵向牵引力的存在导致横向力作用减弱。例如：即使η=1(纵向牵引力全部分配到前轮)，此时只有Yf才有减弱的趋势；当因Xf变化导致Wf减小时，Yf急剧减小，同时Wr增加，Yr得到加强。在此过程中，Yj的具体变化量可以通过改变Xj来调节，因此G向量控制能够提高车辆的稳定性。

3 人在环实时仿真平台

人在环实时仿真系统的总体结构如图2所示。

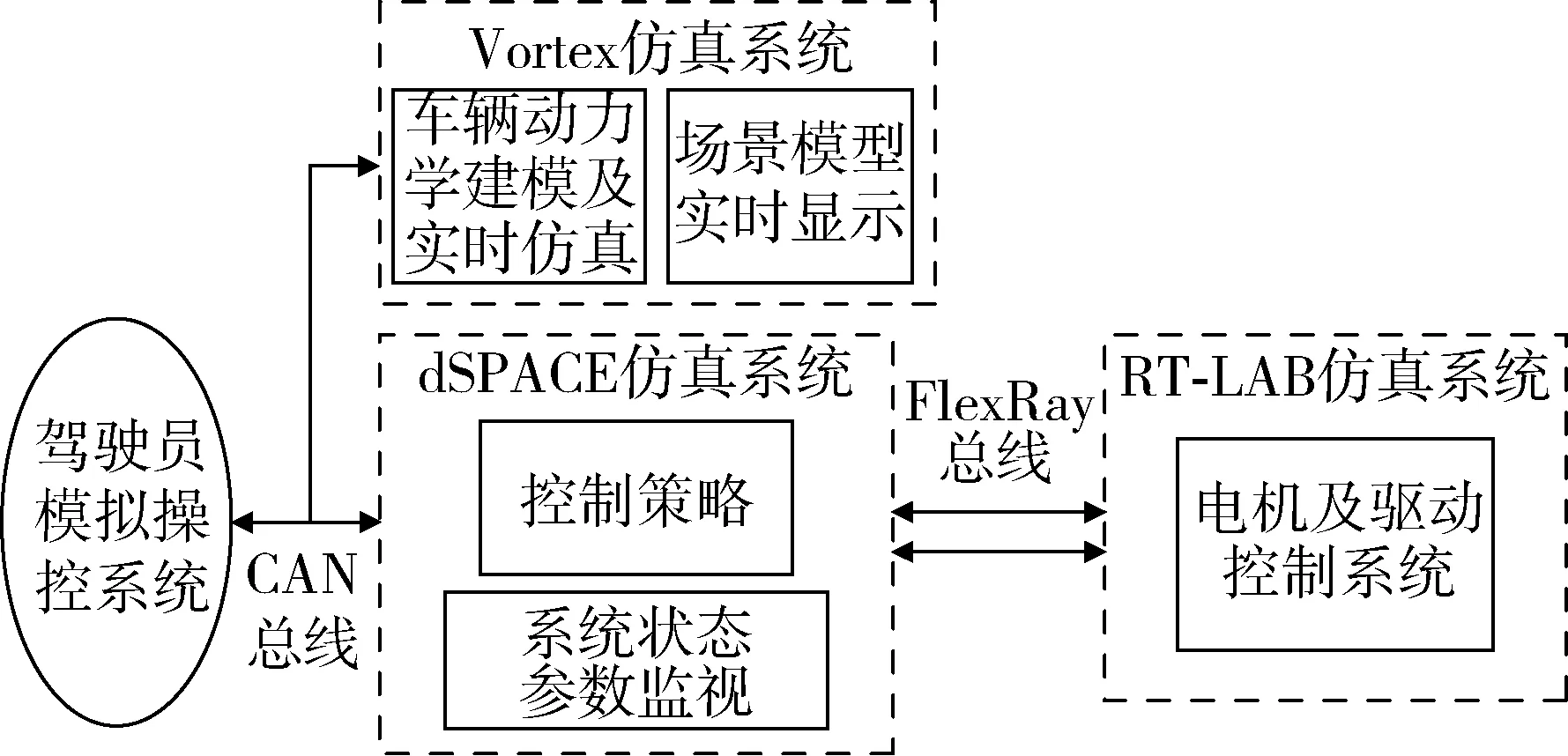
图2 人在环实时仿真平台的总体结构

该系统主要包括4部分：1)驾驶员模拟操纵系统，主要用于采集驾驶员的加速、制动及转向等操控信号；2)dSPACE仿真系统，主要用于车辆行驶控制策略的实时仿真；3)RT-Lab仿真系统，主要用于电机及其驱动控制系统实时仿真；4)Vortex仿真系统，主要用于车辆动力学实时仿真。

实时仿真平台同时采用CAN总线和FlexRay总线，以满足不同控制对象的通讯实时性要求。其中：在驾驶员模拟操控系统、Vortex仿真系统及dSPACE仿真系统间采用CAN总线连接；dSPACE仿真系统与RT-LAB仿真系统间采用FlexRay总线连接。

实时仿真平台具体工作原理为：dSPACE仿真系统根据驾驶员控制指令及车辆状态反馈信息，进行既定车辆行驶控制策略的解算，得到驱动电机给定转矩；RT-LAB仿真系统在接收到转矩给定指令后，结合当前转速信息，经过解算后给出电机实际转矩输出；各驱动电机实际转矩输出值经过折算后作为车轮驱动力矩，在Vortex仿真系统中，直接加载到车辆模型的驱动轮，经过动力学解算后，反馈车辆状态信息；同时，构建仿真场景，实时显示整车运动过程，并利用dSPACE图形界面功能设计整个系统运行状态参数显示界面。

4 实时仿真试验及分析

仿真试验车辆为8×8轮毂电机驱动电传动装甲车辆，车辆及电机驱动系统部分参数如表1所示。

4.1 行驶控制过程分析

蛇行试验是评价车辆稳定性的重要试验，可以考查车辆在接近侧滑或侧翻工况下的操纵性能，以及综合评价车辆的行驶稳定性。试验时，油门踏板开度固定为70%，车辆由静止直线加速至约50 km/h时，分别在无控制和G向量控制2种模式下进行，其方向盘行程变化曲线如图3所示，可见2种控制模式下方向盘转向信号基本一致：在10～15 s期间方向盘右转向，15～20 s期间保持方向盘行程不变，20～25 s期间方向盘回转;在30～35 s期间方向盘左转向，35～40 s期间保持方向盘行程不变，40～45 s期间方向盘回转。

表1 车辆及电机驱动系统部分参数

图3 2种控制模式下方向盘转向行程变化曲线

图4 2种控制模式下总转矩系数变化曲线

图5、6分别为无控制、G向量控制时，各驱动电机给定转矩随时间的变化曲线，可知：1)无控制时，各驱动电机给定转矩完全一致(曲线重合)，并且随车速变化而变化；2)当采用G向量控制时，各驱动电机给定转矩完全一致(曲线重合)，但在转向时，其随图4中的总转矩系数相应变化，符合该控制方法对转矩的控制规律。

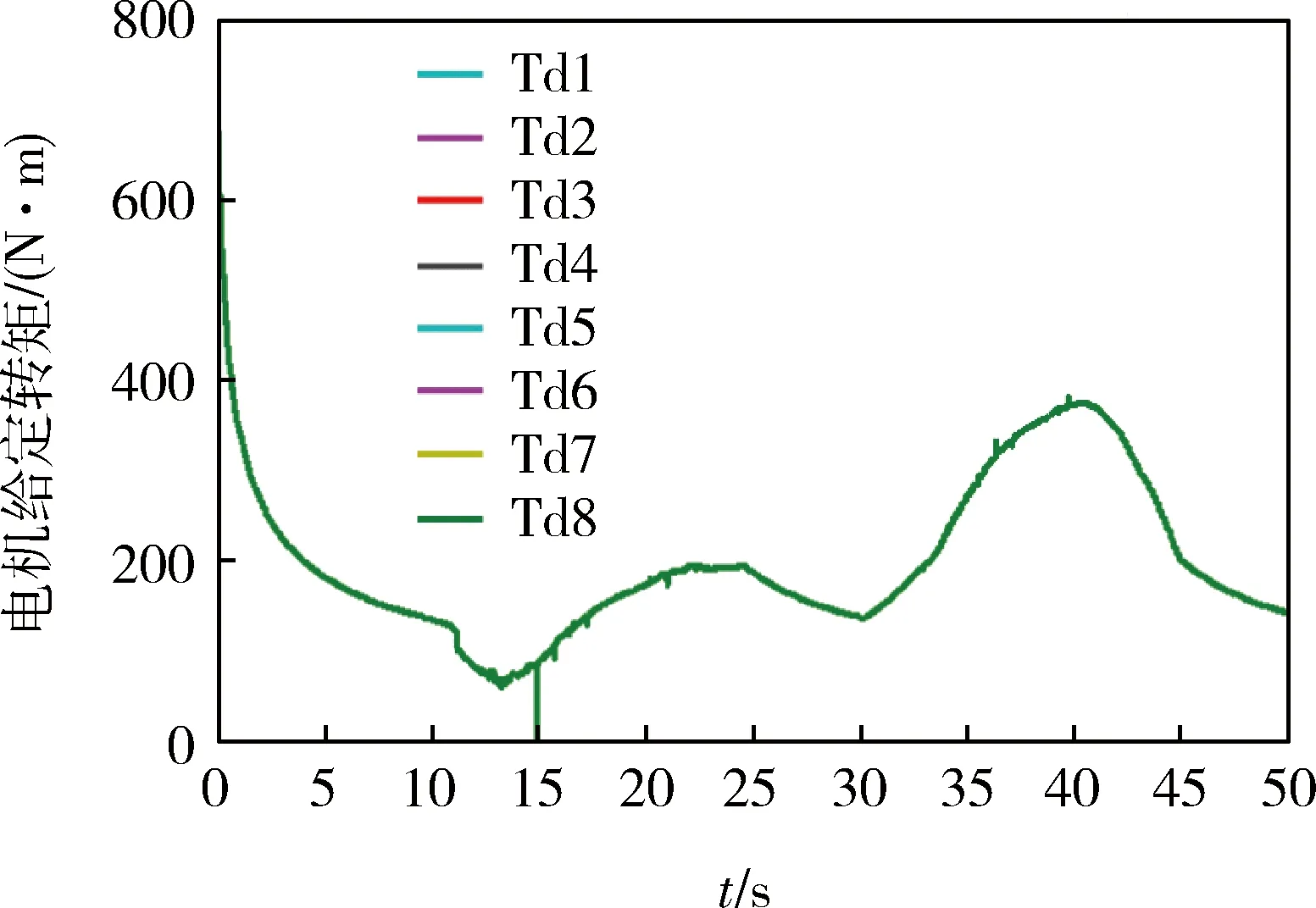
图5 无控制时各驱动电机给定转矩变化曲线

图6 G向量控制时各驱动电机给定转矩变化曲线

图7、8分别为2种控制模式下车辆纵向加速度及车速变化曲线，可知：1)方向盘开始转向时，车辆纵向加速度减小并变为负值，车速也开始降低；2)转向稳定时，车辆纵向加速度恢复到0附近，车速变化缓慢；3)方向盘回转时，车辆纵向加速度增大，车速也迅速增大；4)方向盘完全回正后，车辆纵向加速度减小，车速恢复到初始值(50 km/h)。转向过程中，纵向加速度及车速变化趋势符合图1中G向量控制规则。此外，图7中，虽然右转向2种控制模式下的纵向加速度差别不大，但左转向时的纵向加速度差距较大(最大差值为1 m/s2)，此时，图8中车速差距明显较大(36.5 s时最大为15 km/h)，降速幅度超过50%。

图7 2种控制模式下车辆纵向加速度变化曲线

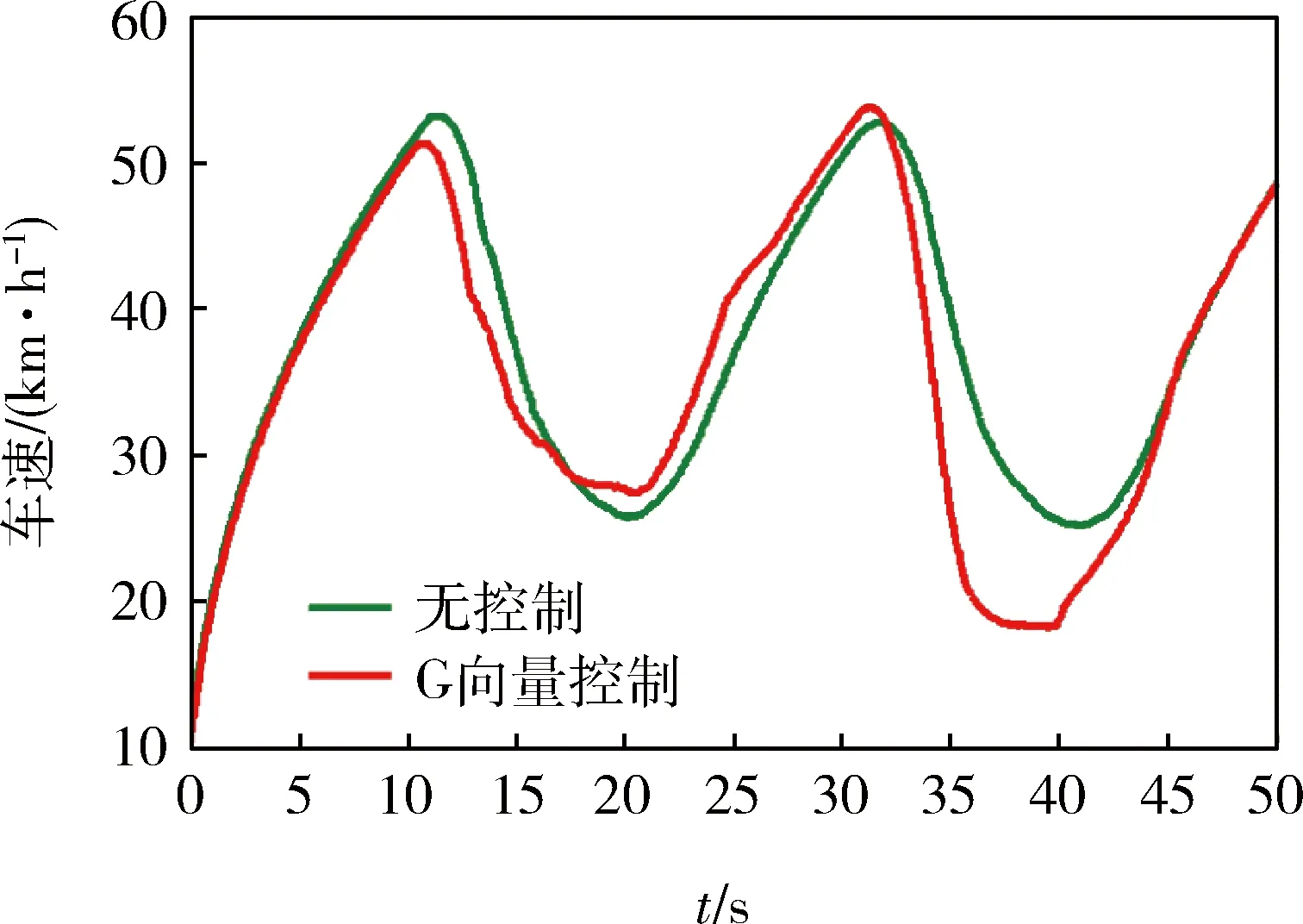
图8 2种控制模式下车辆车速变化曲线

4.2 行驶控制稳定性分析

车辆行驶控制稳定性可用横向加速度随时间的变化规律表示，如图9所示。可以看出：1)无控制时，车辆横向加速度较大，最大值接近10 m/s2；2)当采用G向量控制时，车辆的横向加速度减小，特别是在左转向36.5 s左右时，横向加速度由无控制时的5 m/s2减小到1.5 m/s2。图10为车辆质心侧偏角变化曲线，可知：当采用G向量控制时，车辆质心侧偏角明显减小，其峰值降低接近50%。图11为横摆角速度变化曲线，可知：1)无控制时，车辆横摆角速度变化剧烈，与理论横摆角速度差距较大，特别是当左转向37 s时，超过理论值一倍；2)当采用G向量控制时，车辆横摆角速度基本能够稳定跟随理论参考值，误差值相对较小。总体而言，G向量控制能够提高车辆稳定性。

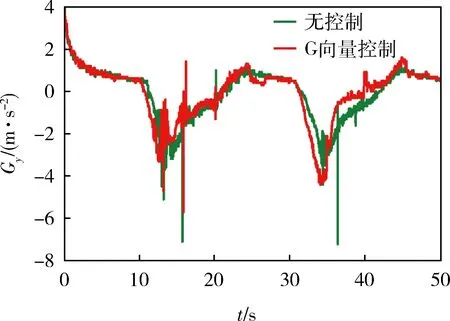
图9 横向加速度变化曲线

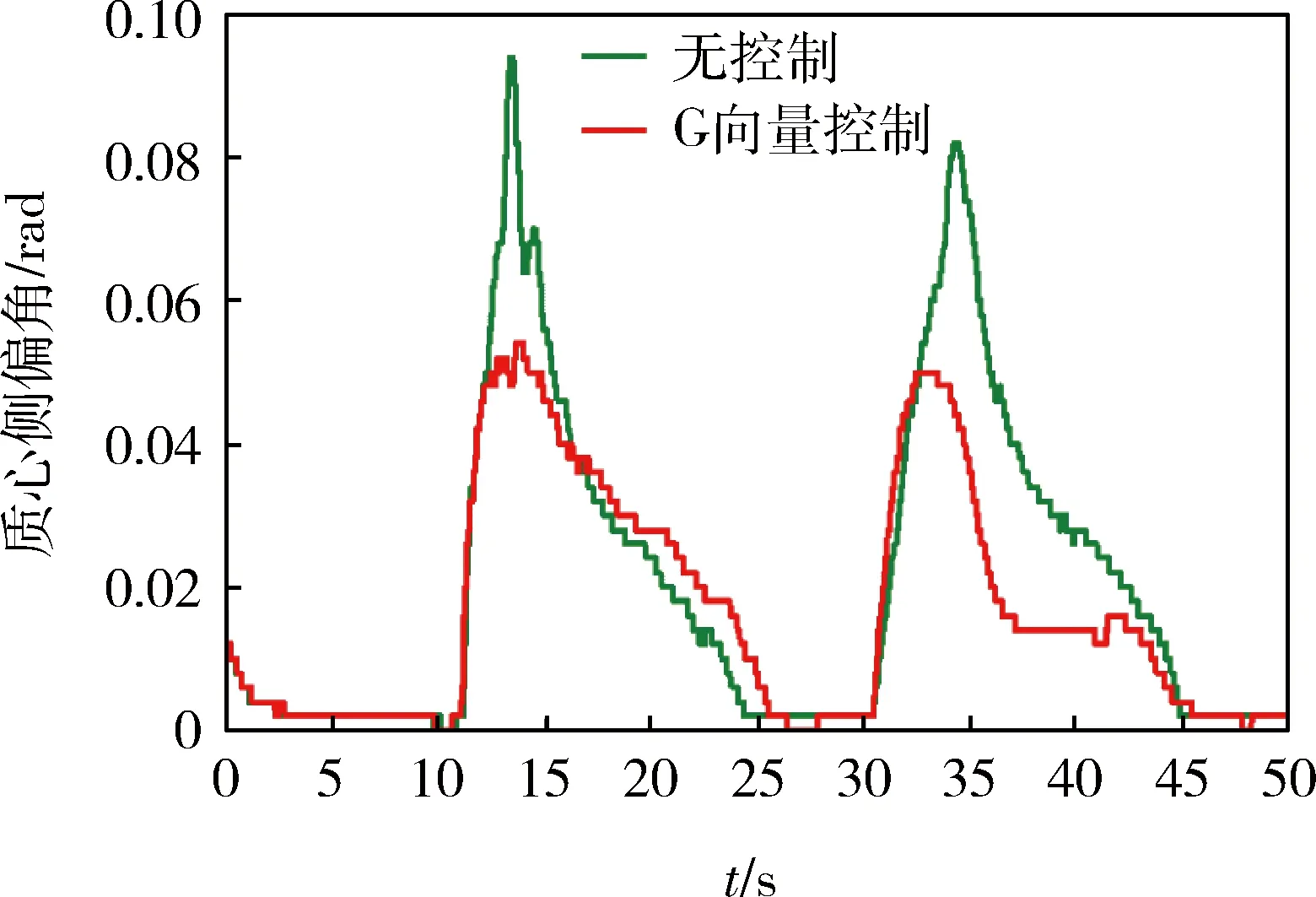
图10 质心侧偏角变化曲线

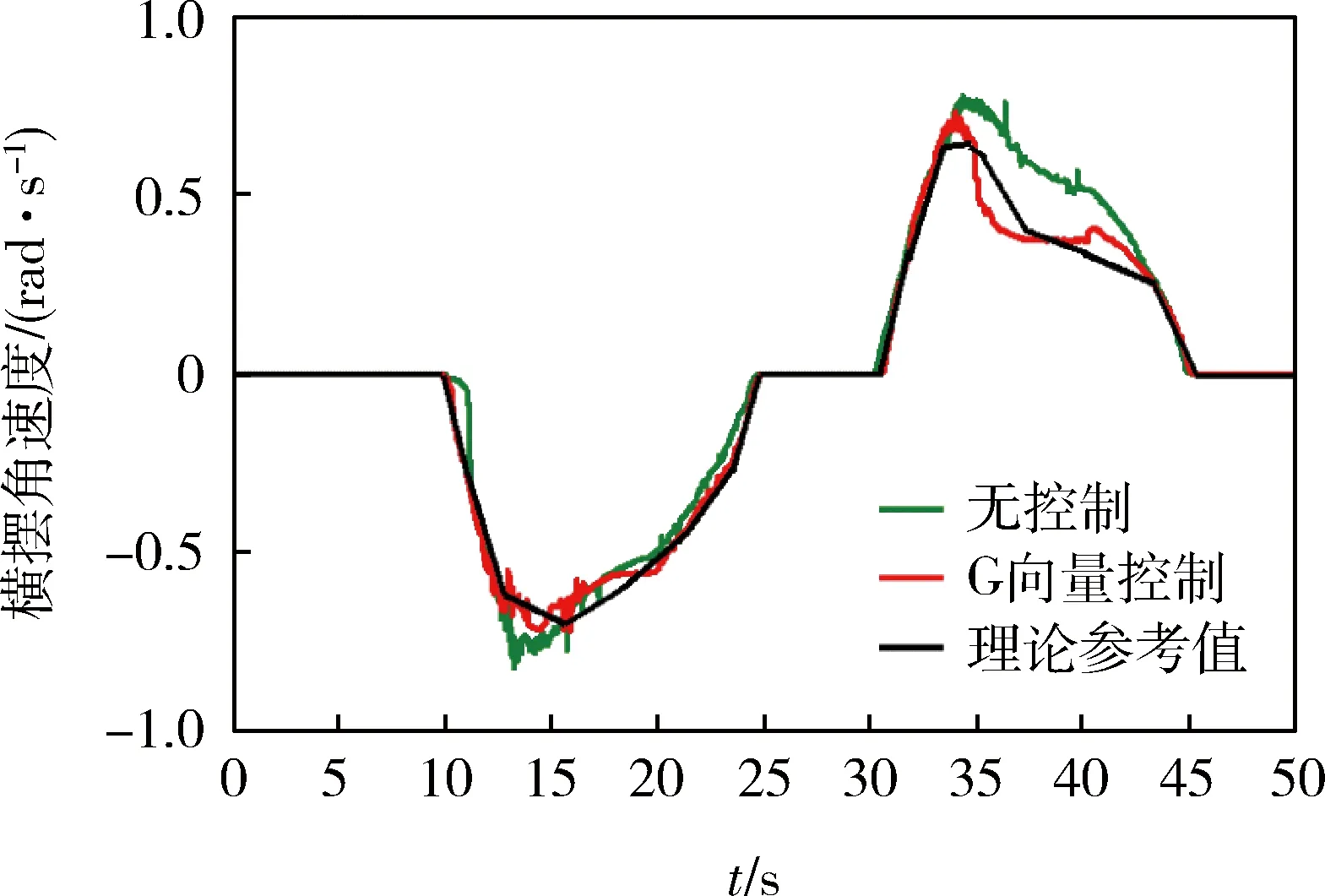
图11 横摆角速度变化曲线

5 结论

本文针对8×8轮毂电机驱动装甲车辆，提出了一种基于G向量控制的多轮独立驱动车辆行驶稳定性控制方法，利用车辆的横向加速度信息调节总驱动力矩,并基于车辆2自由度模型分析了G向量控制的理论依据，通过人在环实时仿真系统进行了实时仿真试验，仿真结果表明：G向量控制能够有效控制车辆的横向运动、抑制车辆的质心侧偏角，从而提高车辆横摆角速度跟随能力和车辆行驶稳定性。该控制方法为多轮独立驱动车辆的行驶稳定性控制提供了新的思路。后续将进一步研究对各独立驱动电机进行转向时的力矩控制，实现总驱动力矩优化控制与单个驱动轮纵向力优化控制相结合，进一步提高车辆的操纵稳定性。

[1] 熊璐，余卓平，姜炜,等.基于纵向力分配的轮边驱动电动汽车稳定性控制[J].同济大学学报，2010，38(3)：417-421.

[2] 邹广才,罗禹贡,李克强.基于全轮纵向力优化分配的4WD车辆直接横摆力矩控制[J]. 农业机械学报，2009，40(5)：1-6.

[3] Ge Y H，Chang C S.A Novel Yaw Stabilization Control System for In-wheel Motor Driven Electric Vehicle[C]∥Proceedings of 6th IEEE Conference on Industrial Electronics and Applications.Beijing:IEEE,2011:1293-1296.

[4] Song J G,Xu P P.The Research of Stability Performance of 4WD Vehicles Basing on Electric Wheels Torque Control [C]∥Proceedings of 2011 IEEE International Conference on Mechatronics and Automation. Beijing:IEEE,2011:354-358.

[5] Kanghyun N,Hiroshi F，Yoichi H.Lateral Stability Control of In-wheel-motor-driven Electric Vehicles Based on Sideslip Angle Estimation Using Lateral Tire Force Sensors[J].IEEE Transactions on Vehicular Technology，2012，61(5)：1972-1985.

[6] 范晶晶，罗禹贡，张海林,等.全轮独立电驱动车辆双重转向控制策略的研究[J].汽车工程，2011，33(5)：369-372.

[7] 苏建强，马晓军，项宇,等.电驱动装甲车辆双重转向控制联合仿真[J].火力与指挥控制，2014，39(11)：128-132.

[8] 刘明春，张承宁，王志福.8×8轮毂电机全轮驱动车辆动力学建模与仿真[J].北京理工大学学报，2014，34(2)：143-147.

[9] Yamakado M，Abe M.An Experimentally Confirmed Driver Longitudinal Acceleration Control Model Combined with Lateral Motion[J].Vehicle System Dynamics,2007, 46(s1):129-149.

[10] Yamakado M，Junya T.Improvement in Vehicle Agility and Stability by G-vectoring Control[J]. Vehicle System Dynamics, 2010, 48:231-254.

[11] Cong G, Mostefai L, Densi M, et al. Direct Yaw-moment Control of an In-wheel-motored Electric Vehicle Based on Body Slip Angle Fuzzy Observer[J].IEEE Transactions on Industrial Electronics, 2009(5):1411-1419.

[12] 苏建强. 8×8轮毂电机驱动装甲车辆行驶控制策略研究[D].北京：装甲兵工程学院，2013.

[13] 付皓. 汽车电子稳定性系统质心侧偏角估计与控制策略研究[D].长春:吉林大学,2008.

[14] Manfred M, Henning W.汽车动力学[M].4版. 陈荫三, 余强,译.北京: 清华大学出版社,2009：473-480.

[15] 袁忠诚.稳态轮胎模型研究[D].长春:吉林大学,2006.

[16] 张缓缓.采用电动轮驱动的电动汽车转矩协调控制研究[D].长春:吉林大学,2009.

(责任编辑:尚菲菲)

Stability Control of Armored Vehicles by Multi-wheel Independent Drive

ZHANG Yun-yin1, MA Xiao-jun1, LIU Chun-guang1, LIAO Zi-li1, ZHNAG Tong-zhen2

(1. Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 2. Department of Training, Shijiazhuang Mechanical Infantry Academy, Shijiazhuang 050083, China)

For stability control of armored vehicles by multi-wheel independent drive, a new kind of drive torque control method based on G-vector is given. The total drive torque is optimized using the vehicle lateral acceleration information. The control feasibility is proved by analyzing the effect of load transmission and longitudinal drive torque based on two-degree-of-freedom vehicle model. This control method is validated based on the driver in-loop real-time simulation system of 8×8 in-wheel motor drive armored vehicle. The simulation results show that the ability to control the lateral motion of the vehicle is improved effectually and the driving stability is improved.

electric drive; multi-wheel independent drive; G-vector control; real-time simulation

1672-1497(2015)05-0026-06

2015-03-30

军队科研计划项目

张运银(1987-)，男，博士研究生。

TJ81+0.34; TP391.9

A

10.3969/j.issn.1672-1497.2015.05.007