一类具反应扩散的捕食模型平衡态模式的定性分析
2015-06-23谢君辉刘婷婷
谢君辉,刘婷婷,孙 涛
(湖北民族学院 理学院,湖北 恩施 445000)
一类具反应扩散的捕食模型平衡态模式的定性分析
谢君辉,刘婷婷,孙 涛
(湖北民族学院 理学院,湖北 恩施 445000)
研究了一类具反应扩散的捕食-食饵模型,运用分歧理论讨论了该模型平衡态半平凡解的局部分支解的存在性,进而,给出了该问题正平衡解存在性的充分条件.
捕食模型;反应;扩散;平衡态
生物数学是生物学与数学之间的学科,它应用数学方法研究和解决生物问题,并对与生物有关的数学方法进行理论研究.捕食-食饵模型是生物数学中的一类重要模型,关于捕食-食饵模型,人们不仅考虑空间分布均匀的常微分方程模型,而且,而且也考虑空间分布不均匀的偏微分方程模型,即具反应扩散的捕食模型.利用反应扩散方程组来研究生物模型,已经成为偏微分方程的一个重要研究方向,同时也成为生物学发展的一个趋势[1-7].由于反应扩散方程组解的长时间行为与其相应的平衡态问题密切相关,因此,确定反应扩散方程组平衡解的定性性质是后续研究的首要环节和任务.
本文就如下捕食模型进行研究:

上述两个模型中,Ω⊂Rn(n≥2)为有界开区域,边界∂Ω充分光滑,λ,μ,a,b,c均为正常数,u,v分别表示在一定的范围Ω内食饵和捕食者物种的密度.本文中,限定μ>0,表明捕食者还有其他的食物来源为HollingIV类功能反应函数(又称Monod-haldance函数).此外,从生态学角度来看,齐次Neumann边界条件表明系统是封闭的.
模型(1)描述在一个封闭的环境里,食饵与捕食者相互影响的关系.模型(2)则刻画在这样的一个封闭环境中,捕食者和食饵的数量能否达到某个共存平衡态.
1 主要结论及证明
引理1[7](基本的分歧定理) 设X,Y为Banach空间,U=S×V为R×X中的开集,f∈C2(U,Y)且f(λ,0)=0,又L0=D2f(λ0,0),L1=D1D2f(λ0,0)满足下列条件:
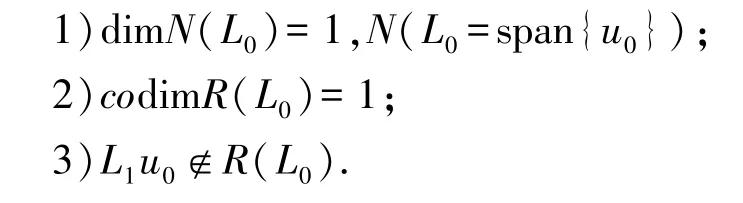
则存在δ>0和C1连续曲线(λ,φ):(-δ,δ)→R×Y使得对任意.而且存在(λ0,0)的领域,使得f的零点或者在这条曲线上,或者为(λ,0).
定理1 假设μ>λ,则模型(2)存在正解(u,v)>(0,0).
证明 首先令μ>λ,将λ取为分歧参数,由半平凡非负解{λ,0,θ[μ]}构造出方程的解,其中θ[μ]为问题:

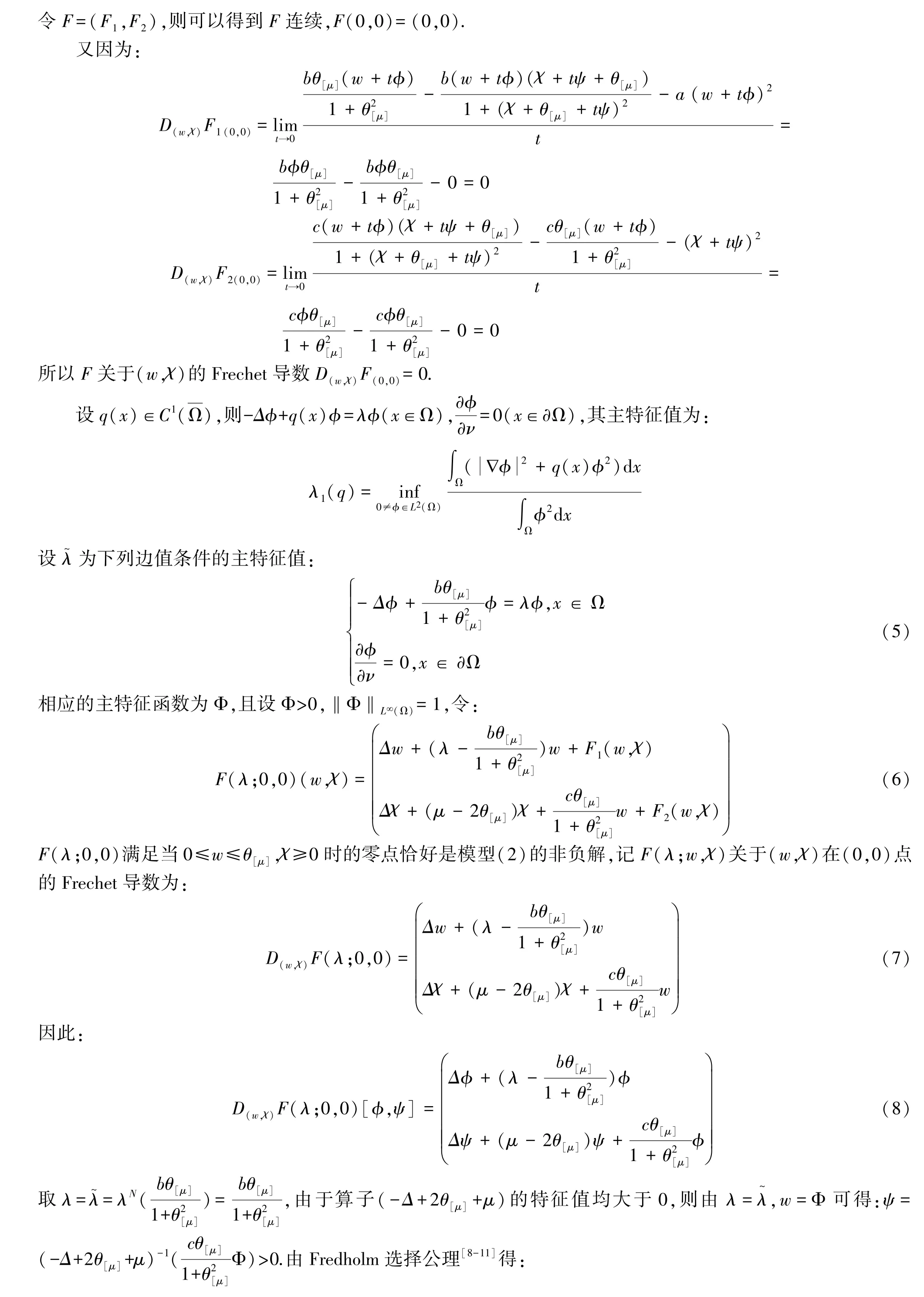


同样有:存在充分小δ>0及C1连续曲线(-δ,δ):→R×Z λ(0)=λ~,φ1(0)=φ2(0)=0且(λ(s);w(s),χ(s))=(λ(s);w(φ+φ1(s)),s(ψ+φ2(s)))满足(λ(s);w(s),χ(s))=0,其中 X=Z⊕span{(φ,ψ)}.因此(λ(s);U(s),V(s))(|s|<δ)是模型(2)的分歧解,其中U(s)=s(φ+φ1(s)),V(s)=s(ψ+φ2(s)).若取0<s<δ,则它恰好为模型(2)的正解,且在分歧点{μ~;θ[λ],0}附近的非平凡负解要么在分支{(λ;0,θ[μ]),λ∈R+}上,要么在{(λ(s);U(s),V(s)),0<s<δ}上,即定理1得证.
[1]郭改慧,李艳玲.B-D反应项的捕食-食饵模型的全局分支及稳定性[J].应用数学学报,2008,31(2):30-40.
[2]郭改慧,吴建华.一类捕食-食饵模型正解的存在性和唯一性[J].武汉大学学报:理学版,2008,54(1):9-14.
[3]吴婷.一类带B-D反应项的捕食食饵模型的解的研究[D].长沙:湖南师范大学,2012.
[4]Peng R,Wang M X,Chen W Y.Positive steady of a prey-predator model with diffusionand nonmonotone conversion rate[J].Acta Math Sin,2007,23(4):749-760.
[5]Peng R,Shi J P,Wang M X.Stationary pattern of a ratio-dependent food chain model with diffusion[J].SIAM J Appl Math,2007,67(5):1479-1503.
[6]肖学良,雒志学,张宇功.一类具有Holling-Ⅱ型功能反应的食饵-捕食者模型的定性分析[J].西南民族大学学报:自然科学版,2013,23(3):190-194.
[7]毛月梅,马小箭.一类具有阶段结构的捕食开发模型的动力学行为[J].延边大学学报:自然科学版,2013,39(2):108-11.
[8]叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1994:118-134.
[9]郭大钧.非线性泛函分析[M].济南:山东科技出版社,2003:42-77.
[10]曾宪忠.带有第三边值的捕食模型的正稳态解的存在性[J].应用数学学报,2006,29(5):801-820.
[11]叶其孝,李正元,王明新,等.反应扩散方程引论[M].2版.北京:科学出版社,2011.
[12]Du Y,Sze-Bi Hsu.A diffusive predator-prey model in heterogeneous environment[J].J Differential Equations,2004,203:331-364.
[13]Zeng X Z.A ratio-dependent predator-prey system with diffusion[J].Nonlinear Anal:RWA,2007,8(4):1062-1078.
[14]彭锐,王明新.一个具有扩散和比例依赖响应函数捕食模型的定性分析[J].中国科学A辑:数学,2011,38(2):135-148.
[15]Zeng X Z,Liu Z H.Nonconstant positive steady states for a ratio-dependent predator-prey system with cross-diffusion[J].Nonlinear Anal:RWA,2010,11(1):327-390.
[16]Yang K.种群数学模型的基本性质[J].生物数学学报,2002,17(2):129-142.
[17]顾永耕,曾宪忠.被捕食者带有第三边值的捕食模型的正稳态解的存在性[J].数学物理学报,2007,A27(2):248-262.
责任编辑:时 凌
Qualitative Analysis of a Class of Predator Pray Model with Reaction Diffusion
XIE Junhui,LIU Tingting,SUN Tao
(School of Science,Hubei University for Nationalities,Enshi 445000,China)
In this paper,we study a class of predator-prey model with reaction and diffusion.By using the bifurcation theory,we discuss the existence of semi-trivial solution for local branch solutions of the steady states and give the sufficient conditions for the existence of positive solutions of the problem.
predator-prey model;reaction;diffusion;equilibrium
O029
A
1008-8423(2015)03-0247-05
10.13501/j.cnki.42-1569/n.2015.09.003
2015-06-16.
湖北省教育厅科学技术研究项目(B2015097);湖北民族学院博士启动基金(MY2013B019);湖北民族学院大学生创新项目(2014Z048).
谢君辉(1985-),女,博士,讲师,主要从事偏微分方程理论及应用的研究.
