基于多数包含关系的广义变精度粗糙集模型
2015-06-23黄卫华冯云再陆亚哲
黄卫华,冯云再,陆亚哲
(文山学院数学学院,云南 文山 663000)
基于多数包含关系的广义变精度粗糙集模型
黄卫华,冯云再,陆亚哲
(文山学院数学学院,云南 文山 663000)
通过分析Ziarko变精度粗糙集模型的不足,引入误差参数α(0≤α<0.5),定义了基于多数包含关系的广义变精度粗糙集模型;讨论了该模型中α上、下近似算子的性质;验证了当|RP(x)|·α=k时,广义变精度粗糙集模型退化为程度粗糙集模型;最后,举例说明了该模型在数据挖掘中的应用.
粗糙集;近似算子;多数包含关系;广义变精度粗糙集
1982年波兰数学家帕夫拉克提出的粗糙集理论[1]是按照等价关系来分类的,因而它的分类是精确的,即要么“包含”,要么“不包含”,而没有程度上的“包含”或“属于”,那么它所处理的分类就必须是完全正确的或肯定的.变精度粗糙集模型克服了以上局限,在分类过程中,变精度粗糙集模型允许等价类有一定的错误分类率,这是对经典粗糙集模型很好的推广.Pawlak粗糙集模型的这些缺点限制了它的广泛应用.为了弥补这些不足,许多学者从不同角度推广了经典粗糙集模型[2-7〛[8],定义了基于多数包含关系的广义变精度粗糙集模型,证明了当α=0时,模型退化为经典粗糙集模型;当|RP(x)|·α=k时,退化为一般关系下的程度粗糙集模型[9〛;当二元关系R为论域U上的等价关系时,模型退化为Ziarko变精度粗糙集模型.
1 预备知识
为了便于下文的论述及相关性质的研究,本节首先给出以下需要用到的一些基本概念.
定义1[9]设R⊆U×U是论域U上的任意二元关系,∀x,y∈U,若xRy,即(x,y)∈R,则称x是y的前继,y是x的后继,记Rs(x)={y∈U|xRy},Rp(x)={y∈U|yRx},分别称为x的后继邻域和前继邻域.
定义2[1]设U为非空有限论域,R是U上任意的二元关系,称A=(U,R)为广义近似空间.∀X⊆U,分别定义X关于广义近似空间A的上、下近似,正域,边界和负域为:
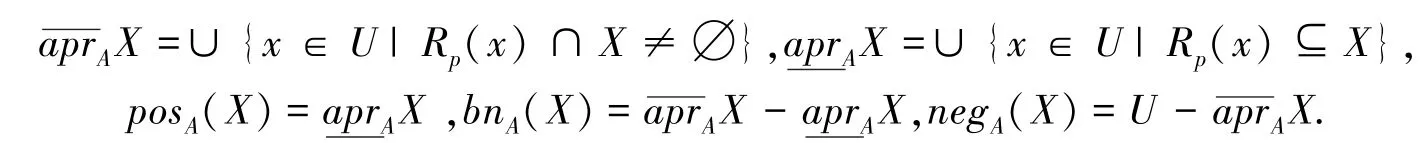
定义3[9]设A=(U,R)是一个广义近似空间,X(X≠∅)⊆U,k为非负整数,定义X关于近似空间A依程度k的下近似和上近似分别为:
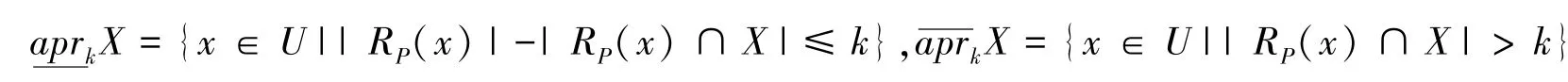
其中|RP(x)|表示集合RP(x)的基数.
定义4[8]设X是有限论域U的两个非空子集,R是U上任意的二元关系,若∀y∈RP(x),都有y∈X,则称X包含RP(x),记作X⊇RP(x).令:
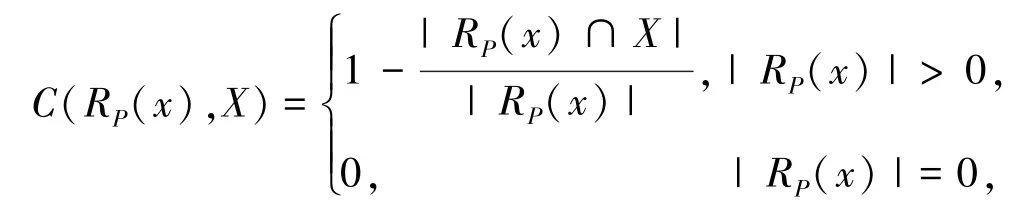
称C(RP(x),X)为集合RP(x)关于集合X的相对错误分类率.设,则一般关系下的多数包含关系定义为X
定义5[1]设(U,R)为近似空间,其中U为非空有限论域,R为U上的等价关系,U/R={E1,E2,…,En}为R的等价类构成的集合.∀X⊆U,0≤α<0.5,分别定义X的α上、下近似,边界和负域为:

定义6[9]设A=(U,R)是广义近似空间,其中U为非空有限论域,R为U上的任意二元关系,∀X⊆U,0≤α<0.5,定义X的α上、下近似,正域,边界和负域为:

2 主要结果
再证必要性:若C(RP(x),X)=0,则



[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.
[2]巩增泰,孙秉珍,邵亚斌,等.一般关系下的变精度粗糙集模型[J].兰州大学学报,2005,41(6):110-114.
[3]孙士保,姚磊磊,吴庆涛,等.变精度粗糙集模型及其应用研究[J].计算机工程与应用,2009,45(7):10-19.
[4]王兆浩,舒兰,丁修勇.几种粗糙集模型的推广研究[J].计算机工程与应用,2011,47(36):68-72.
[5]申锦标,吕跃进.变精度与程度粗糙集的一种推广[J].计算机工程与应用,2008,44(36):45-47.
[6]闫敏伦.新型变精度多粒化粗糙集模型[J].南京理工大学学报,2014,38(4):496-500.
[7]许韦,吴陈,杨习贝.基于相似关系的变精度多粒度粗糙集模型[J].科学技术与工程,2013,13(9):2517-2522.
[8]ZIARKO W.Variable precision rough set modle[J].Journal of Computer and System Sciences,1993,46(1):39-59.
[9]张文修,吴伟志.粗糙集理论与方法[M].北京:科学出版社,2001:55-56.
责任编辑:时 凌
Generalized Variable Precision Rough Set Model Based on the Majority of Inclusion Relation
HUANG Weihua,FENG Yunzai,LU Yazhe
(School of Mathematics,Wenshan University,Wenshan 663000,China)
To make up for the drawbacks of general relations of rough set model,we introduce error pa⁃rameter α(0≤α<0.5)and define the generalized variable precision rough set model based on the majori⁃ty of inclusion relation.The properties of α upper and lower approximation operators are discussed in the model.Meanwhile,if|RP(x)|·α=k,it is the degraded rough set model.Finally,examples are given to show that this model can be applied to data mining.
rough set;opproximate operator;majority of inclusion relation;generalized variable preci⁃sion rough set model
TP18
A
1008-8423(2015)03-0260-04
10.13501/j.cnki.42-1569/n.2015.09.006
2015-05-26.
国家自然科学基金项目(11361074);云南省教育厅基金项目(2015Y470);文山学院科研基金项目(14WSY01);文山学院重点学科数学建设项目(12WSXK01);文山学院高等代数精品课程.
黄卫华(1979-),女,硕士,讲师,主要从事信息代数、半群和粗糙集理论研究.
