曲线上的Frenet标架

包图雅，张 陆

（内蒙古民族大学数学学院，内蒙 古通辽 028043）

曲线上的Frenet标架

包图雅，张 陆

（内蒙古民族大学数学学院，内蒙 古通辽 028043）

利用施密特正交化方法求出了曲线上一点处的Frenet标架，并讨论了Frenet标架中三个基本向量的方向.

曲线；Frenet标架；基本向量；施密特正交化方法

曲线上的Frenet标架场对研究曲线一点邻近结构以及建立曲线论基本定理有着重要意义.例如，文献［1］中利用Frenet标架考虑了曲线的生成以及曲面间的保长变换的软件实现.通过Frenet标架场，E3中的一条正则曲线变成正交标架空间中的一条曲线［2］．

定义1［3］设曲线C：r＝r（t），a＜t＜b为C2类曲线，若对于曲线C上一点P（t＝t0）有r′（t0）≠0，则称该点为曲线C的正常点，当曲线C上每一点都是正常点时称曲线C为正则曲线．若对于曲线C上一点P（t＝t0）有r′（t0）×r″（t0）≠0，则称该点P（t＝t0）为曲线C的非逗留点．

本文中约定所讨论的曲线上的任意一点都既是正常点，又是非逗留点．

文献［2－4］中给出了弧长参数下曲线上一点的Frenet标架的定义，如下：

定义2［2－4］给定C2类曲线C上一点P（s），设曲线C的向量式参数方程为C：r＝r( s)，0＜s＜L（C），其中s为弧长参数．称为曲线上点P（s）处的单位切向量；称为曲线上点P( s)处的主法向量；称γ＝α×β为曲线上点P（s）处的副法向量；称两两正交的单位向量组α，β，γ为曲线上点P（s）处的Frenet标架.

文献［2－4］又给出了关于一般参数下曲线的Frenet标架.如下：

命题1［2－4］给定C2类曲线C上一点P（t），设曲线C的向量式参数方程为r＝r（t），a＜t＜b，其中t为一般参数，则Frenet标架中三个基本向量分别为：

虽然文献［2－4］中并没有给出该命题的证明过程，但从Frenet标架中基本向量的表示顺序可知命题1的结论是利用了副法向量其垂直于密切平面的性质得出的.文献［5］以一般参数t为中间变量并利用基本向量的定义以及向量函数求导法则给出了基本向量的表示.

命题2［6－7］（Gram－schmidt正交化方法） 设α1，α2，…，αr（r≤n）是欧式空间Rn中线性无关的向量组，则由如下方法：

本文将利用施密特正交化方法推导一般参数下曲线在一点处的Frenet标架中三个基本向量，并讨论基本向量α，β，γ的方向．

2 主要结果

定理1 给定C2类正则曲线C，设P（t）是曲线C上任意一点，而曲线C的向量式参数方程为：r＝r（t），a＜t＜b，其中t为一般参数，则Frenet标架中三个基本向量分别为：

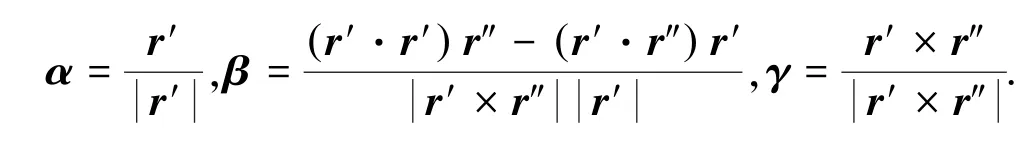
证明 由于曲线C是正则曲线，因此r′（t）≠0．又因为曲线没有停留点且是C2类的，从而r″（t）存在且r′（t）×r″（t）≠0成立，所以向量组是线性无关的向量组．由施密特正交化方法取′，再把ε1，ε2单位化，就可以表示出基本向量α，β，再利用向量积的性质可表示出γ．

接下来讨论三个基本向量的方向．由Frenet标架的定义以及向量积知识［8］可知三个基本向量中只要确定其中两个向量的方向剩下一个向量的方向可随之而定．文献［1］中定义切向量的方向与曲线的正向一致，因此本文中着重讨论了主法向量的方向．

定理2 给定C2类正则曲线C，设P（t）是曲线C上任意一点，而曲线C的向量式参数方程为r＝r（t），a＜t＜b，其中t为一般参数．则曲线上每一点处Frenet标架中主法向量β与曲线的向量函数的二阶微商r″（t）总是在切线的同一侧，并且主法向量总是指向曲线凹入的一侧．

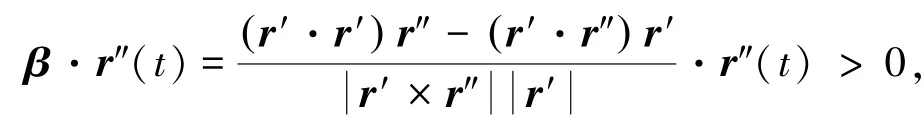
例1可以作为定理1和定理2的应用．

例1 求螺旋线x＝cost，y＝sint，z＝t在点（1，0，0）处的基本向量α，β，γ．

解 由所给曲线得r＝｛cost，sint，t｝，在点（1，0，0）处参数t＝0，可计算出：

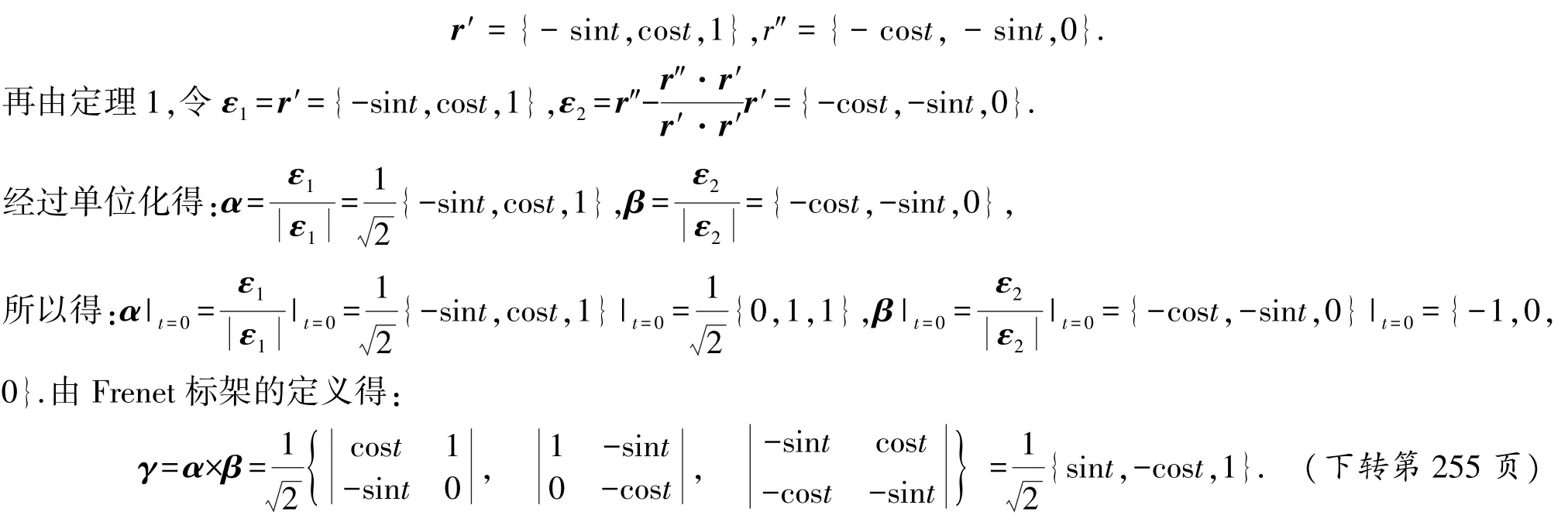
在上述例子计算过程中可观察到向量r″（t）与向量β相等，又由于r″（t）的方向指向曲线凹入的一侧，从而β的方向也指向曲线凹入的一侧．

［1］范荣辉，岳崇山.Frenet标架运动生成曲线与曲面间的保长变换的软件实现及思考［J］.唐山师范学院学报：自然科学版，2008，30（2）：26－29.

［2］陈维桓.微分几何初步［M］.北京：北京大学出版社，1990：10－24.

［3］梅向明，黄敬之.微分几何［M］.4版.北京：高等教育出版社，2008：13－36.

［4］吴大任.微分几何讲义［M］.北京：人民教育出版社，1959：13－52.

［5］岳崇山，刘建斌.关于曲线在一点的基本三棱形的探讨［J］.河北北方学院学报：自然科学版，2007，23（4）：15－18.

［6］华中科技大学数学系.线性代数［M］.3版.北京：高等教育出版社，2008：102－105.

［7］北京大学数学系.高等代数［M］.2版.北京：高等教育出版社，1988：367－370.

［8］吕林根，许子道.解析几何［M］.4版.北京：北京大学出版社，2006：47－51.

责任编辑：时 凌

Frenet Frame on a Curve

BAO Tuya，ZHANG Lu

（College of Mathematics，Inner Mongolia University for the Nationalities，Tongliao 028043，China）

In this paper we obtain Frenet frame by schmidt orthogonalization method and discuss the di⁃rection of three fundamental vectors in Frenet frame.

curve；Frenet frame；fundamental vector；schmidt orthogonalization method

0186.1

A

1008－8423（2015）03－0245－03

10.13501／j.cnki.42－1569／n.2015.09.002

2015－06－12.

内蒙古自然科学基金项目（2013MS0112）；内蒙古民族大学科学研究基金项目（NMDGP1416）.

包图雅（1980－），女（蒙古族），博士，副教授，主要从事微分几何研究.