平面上的广义Bonnesen型不等式

朱保成

（湖北民族学院 数学系，湖北 恩施 445000）

平面上的广义Bonnesen型不等式

朱保成

（湖北民族学院 数学系，湖北 恩施 445000）

研究了平面上的广义Bonnesen型不等式.获得了平面上Aleksandrov－fenchel不等式的加强形式，这些加强形式是经典Bonnesen型不等式的推广.更一步地，还得到了平面上Aleksandrov－fenchel不等式的上界结果，这些不等式都很好地刻画了凸集的相对均质积分的性质.

均质积分；Steiner公式；Bonnesen型不等式；Aleksandrov－fenchel不等式

设κn表示ℝn中所有紧致凸集所构成的集合，表示ℝn中所有凸体（具有非空内点的紧致凸集）的集合．设集合K⊂ℝn，它的体积（即n维Lebesgue测度）记为V（K）．令ωn表示n维单位球B的体积．凸集K和E的Minkowski和定义为K＋E＝｛x＋y：x∈K，y∈E｝，凸集K和实数t的Minkowski数乘定义为tK＝｛tx：x∈K｝．

设K1，K2，…，Km是ℝn中紧致凸集，K1，K2，…，λm≥0，则λ1K1＋λ2K2＋ ＋λmKm的体积是关于 λ1，λ2，…，λm的n阶齐次多项式，即：

其中系数V（Ki1，Ki2，…，Kin）是非负的且关于指标对称，称之为Ki1，Ki2，…，Kin的混合体积［1－3］．混合体积具有非常重要的单调性，即：令两凸集K，L∈κn满足K⊂L，而K2，K3，…，Kn∈κn是任意的凸集，则有：

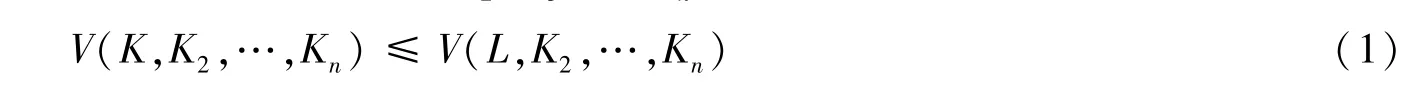
混合体积的另外一个重要性质是它的Minkowski线性性，即：∀K，L，K2，…，Kn∈Kn和A，p≥0，则有：

著名的Minkowski Steiner公式（或相对Steiner公式）事实上是外平行体K＋sE的体积关于s的n阶多项式，即：

其中系数Wi（K；E）称为K关于E的相对均质积分，它们是混合体积的特殊形式．特别地，W0（K；E）＝V（K）和Wn（K；E）＝V（E）．当E＝B时，式（3）右边的多项式就成了经典的Steiner多项式［4］，此时Wi（K；B）简记为Wi（K）并称为K的经典的i－阶均质积分［1－3］．在这种情况下，nW1（K）是K的表面积S（K）且W0（K）＝V（K），Wn（K）＝ωn．

K关于E的相对内半径r（K；E）和相对外半径R（K；E）分别定义如下：

当E＝B时，r（K；B）＝r（K）且R（K；B）＝R（K），分别是K的经典的内切圆半径和外接圆半径［1，5］．

在平面上内半径，外半径及均质积分由著名的Bonnesen型不等式相互联系在一起：设K∈κ2且∈，则有：

该式的证明是由Blaschke给出的［6］，而Bonnesen本人证明了当E＝B的情形［7］．这个不等式加强了Aleksan⁃drov－fenchel不等式，即式（4）加强了如下不等式的2维情形：设K∈κ2且∈，则有：

当K与E位势，即K＝λE＋x（λ≥0，x∈ℝn）时，等号成立．

事实上，不等式（5）就是著名的Aleksandrov－fenchel不等式的特殊形式.这些不等式都给出了相对均质积分的很好的性质，关于相对均质积分的研究可参看文献［8－12］，而这些不等式又是经典的Bonnesen型不等式的推广［7，13－20］.

将利用凸体的体积刻画平面情形的Aleksandrov－fenchel不等式的加强形式.为此，还需要下面的非常重要的命题．

命题1［6］设K∈κ2且∈κ20，则有：

此时，式（7）和式（8）的左边＝0＝右边，故当E＝B且K是一个圆盘时，不等式（7）和式（8）等号成立．将式（7）和式（8）两边同时相加，并平方可得：

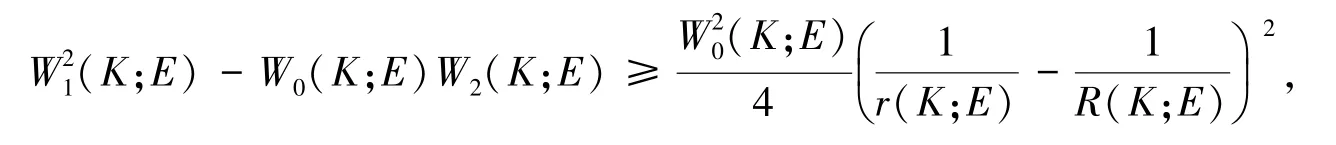
因为W0（K；E）＝V（K），故不等式（7）得证．

将式（7）的两边同时乘以R（K；E），式（8）两边同时乘以r（K；E），再相加可得：

当K与E位势时，式（10）和式（11）等号成立．

另一方面，因为：r（K；E）E⊂K⊂R（K；E）E，结合混合体积的单调性（式（1））和线性性（式（2））可得：

如同定理1的证明过程中等号成立条件的论述一样可知，当E＝B且K是一个圆盘时，式（12）和式（13）等号成立．综合式（10）～（13）即可证得引理．

定理2 在ℝ2中，设E是一个固定凸体及K是任意凸体，则有：

［1］Schneider R.Convex Bodies：The Brunn－MinkowskiTheory［M］.Cambridge：Cambridge University Press，1993.

［2］Gardner R J.Geometric tomography［M］.Cambridge：Cambridge Univ Press，1995.

［3］Gruber P M.Convex and Discrete Geometry［M］.Berlin Heidelberg：Springer，2007.

［4］Steiner J.Uber parallele Flachen［J］.Monatsber Preuss Akad Wiss，1840：114－118［Ges.Werke，Vol II（Reimer，Berlin，1882）245－308］.

［5］Bonnesen T，Fenchel W.Theorie der konvexen Korper［M］.Berlin：Springer，1974.English translation：Boron L，Christenson C，Smith B.（eds.）Theory of convex bodies.Moscow：BCS Associates，1987.

［6］Blaschke W.Vorlesungen iiber Integralgeometrie［M］.3rd edn.Berlin：Deutscher Verlag der Wis－senschaften，1995.

［7］Bonnesen T.Les problemes des isoperimetres et des isepiphanes［M］.Paris：Collection de monographies sur la theorie des fonctions，Gauthier－Vil⁃lars，1929.

［8］Henk M，Hernandez Cifre M A.Notes on the roots of Steiner polynomials［J］.Rev Mat Iberoamericana，2008，24：631－644.

［9］Hernandez Cifre M A，Saorin E.On the roots of the Steiner polynomial of a 3－dimensional convex body［J］.Adv Geom，2007，7：275－294.

［10］Hernandez Cifre M A，Saorin E.On inner parallel bodies and quermassintegrals［J］.Israel J Math，2010，177：29－48.

［11］Hernandez Cifre M A，Saorin E.Differentiability of quermassintegrals：A classification of convex bodies［J］.Tran Amer Math Soc，2014，366：591－609.

［12］Zhu B，Xu W.On the ith quermassintegral of inner parallel bodies（in Chinese）［J］.Sci Sin Math，2015，45：1687－1698.

［13］Bonnesen T.Ubereine Verscharfung der isoperimetrischen Ungleichheit des Kreises in der Ebene and auf der Kugeloberflache nebst einer Anwend⁃ung auf eine Minkowskische Ungleichheit fur konvexe Korper［J］.Math Ann，1921，84：216－227.

［14］Osserman R.Bonnesen－style isoperimetric inequality［J］.Amer Math Monthly，1979，86：1－29.

［15］Xia Y，Xu W，Zhou J，et al.Reverse Bonnesen style inequalities in a surface XE of constant curvature［J］.Sci China Math，2013，56：1145－1154.［16］Xiong G，Cheung W，Li D.Bounds for inclusion measures of convex bodies［J］.Adv Appl Math，2008，41：584－598.

［17］Zeng C，Ma L，Zhou J，Chen F.The Bonnesen isoperimetric inequality in a surface of constant curvature［J］.Sci China Math，2012，55：1913－1919.［18］Zhang G.Geometric inequalities and inclusion measures of convex bodies［M］.Mathematika，1994，41：95－116.

［19］Zhou J.On Bonnesen－type inequalities［J］.Acta Math Sinica（Chinese Series），2007，50：1397－1402.

［20］Zhou J，Ren D.Geometric inequalities－from integral geometry point of view［J］.Acta Math Scientia，2010，30：1322－1339.

责任编辑：时 凌

The General Bonnesen－type Inequalities on Plane

ZHU Baocheng
（Department of Mathematics，Hubei University for Nationalities，Enshi 445000，China）

This paper studies the general Bonnesen type inequalities on plane.We get the stronger Alek⁃sandrov－fenchel inequalities on plane，which are extensions of the classical Bonnesen type inequalities. Moreover，we also give the upper bounds for the Aleksandrov－fenchel inequalities on plane.

quermassintegral；Steiner formula；Bonnesen－type inequality；Aleksandrov－fenchel inequality

01841

A

1008－8423（2015）03－0241－04

10.13501／j.cnki.42－1569／n.2015.09.001

2015－07－16.

国家自然科学基金项目（11501185）；恩施州科学技术局项目（恩州科业［2014］21号）；湖北民族学院博士启动基金项目（MY2014B001）.

朱保成（1980－），男，博士，讲师，主要从事积分几何与凸几何分析的研究.