正交各向异性磁电弹性圆板的哈密顿体系方法

王莉娜，何文明

(温州大学数学与信息科学学院，浙江温州 325035)

正交各向异性磁电弹性圆板的哈密顿体系方法

王莉娜，何文明

(温州大学数学与信息科学学院，浙江温州 325035)

基于哈密顿体系求解方法，针对具有轴对称性的正交各向异性磁电弹性圆板的弯曲问题进行求解．解决问题的基本思路为：首先将该问题的基本方程导入哈密顿体系，得到哈密顿方程；然后研究哈密顿方程的零本征值对应的本征解；最后得到原问题的解析解．与该问题的其它求解方法相比较，哈密顿体系方法具有明显的优越性．

正交各向异性；哈密顿体系方法；本征解；磁电弹性圆板

随着各种各样智能材料的不断涌现，人们对压电材料和压磁材料的研究更为深入，尤其是将压电和压磁材料有机结合起来的复合材料更是引起了广大学者的极大关注．早在1972年，Van Suchtelen就指出，压电和压磁材料的结合会导致新的材料特性即磁电耦合效应的出现[1]，随后，于1974年，Van Run和Van Den Boomgaar等学者对BaTiO3-CoFe2O4压电、压磁复合材料进行了测定，得到该材料具有非凡磁电耦合效应的结论[2]．之后，这种具有独特非凡的磁电耦合效的智能材料在工程中得到了广泛应用．在弹性力学中，求磁电弹性圆板的解析解是一个经典问题．文献[3]给出了横观各向同性层合圆板轴对称弯曲问题的解析解，文献[4]得到了弹性薄板混合边界问题的解析解，文献[5]用边界积分法分析了薄圆板，文献[6-8]也用不同方法求得解析解．就作者所知，目前尚未有文献采用哈密顿体系方法对正交各向异性磁电弹性圆板的弯曲问题进行解析求解．本文将采用文献[9]提出的哈密顿体系方法，对正交各向异性磁电弹性圆板进行解析求解．具体思路为：首先将该问题的基本方程导入哈密顿体系，通过分离变量得到哈密顿方程；然后将原问题转变为哈密顿空间算子矩阵的本征问题，研究哈密顿方程的零本征值对应的本征解，再对本征解的各阶约当型分析求解，这样理性地推导下去；最后得到问题的解析解．哈密顿体系方法是一种普通、理性的方法，采用该方法求解具有明显的优越性．

1 正交各向异性磁电弹性圆板弯曲问题的基本方程

选取柱坐标（r,θ,z），其中r表示圆板的径向坐标，θ表示圆板的角度坐标，z表示圆板的对称轴，坐标原点在材料的对称轴中点处．材料厚度设为2h，直径设为2a．下面将给出正交各向异性磁电弹性圆板弯曲问题的基本方程．

应力平衡方程和电学、磁学方程为：

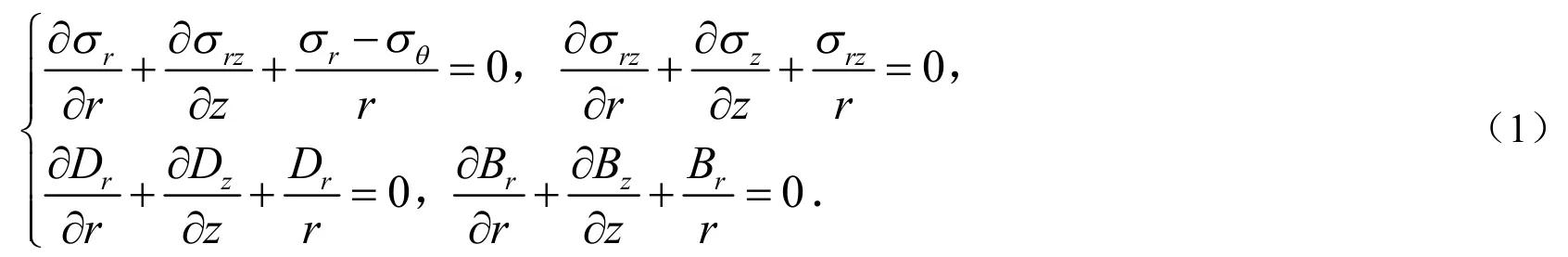
磁电弹性圆板的本构方程为：

其中，cij为弹性刚度系数，eij为压电常数，qij为压磁常数，βii为介电常数，dii为磁电常数，μii为磁性常数；Ei, Hi分别为电场强度和磁场强度；u, w为位移，Dr, Dz为电位移，Br, Bz为磁感应强度；φ, φ分别为电势和磁势；σij为应力，εij为应变．

由于本文研究的磁电弹性圆板具有轴对称性，故环向位移为零，且与环向有关的剪切力以及电位移和磁感应强度也为零．因此在本构方程和以后的计算中都不再考虑．

为简单起见，假设物体表面不受体力，也没有自由电荷与磁场作用．这样拉格朗日系统下的拉格朗日函数可以表示为：L（ u, w,φ, φ）=U（u,w,φ,φ），势能可由以下积分表示：

2 导入哈密顿体系

在对问题进行求解之前，首先通过勒让德变换给出该问题的哈密顿体系描述．令原变量q=｛u, w,φ, φ｝Τ，引入对偶变量p=｛p1, p2,p3,p4｝Τ，对偶变量可由以下方法获得：

由（1）式、（2）式和（7）式得：

3 问题的零本征解及其约当型

上面采用哈密顿体系方法给出了具有轴对称的正交各向异性磁电弹性圆板弯曲问题对应的方程．现在要在此基础上对该方程进行求解，采用的主要方法是分离变量法：令ν=ΨZ（ z ），其中Z（ z）是有关z的函数，Ψ是与z无关的2n维向量．将ν=ΨZ（ z）代入（9）式，得到：

这里λ是本征值，而Ψ是本征向量．

因为存在自由边界，原问题必然存在零本征解，而且零本征向量会存在阶数不同的约当型，不同形式的约当型解被赋予不同的物理意义．

3.1 零本征值本征解

当λ=0时，寻求其本征解，此时（10）式可变为：

求解上式，可得到零本征值的本征解：

对应的物理意义分别为：沿轴向的刚体平移、电势的整体移动、磁势的整体移动．

3.2 各阶约当型本征解

对于零本征解，有方程：

如果（13）式存在既符合问题的边界条件，同时也满足（14）式的本征解，那么就称其为零本征解的第n+1阶约当型解．这里要说明的是，第n阶约当型解都不是原问题的解，但是可以利用它们得到原问题的解．具体来说，原问题的解可以表示为：

1）一阶约当型解

利用方程（13）得到一阶约当型的控制方程为：

对该方程进行求解，得到：

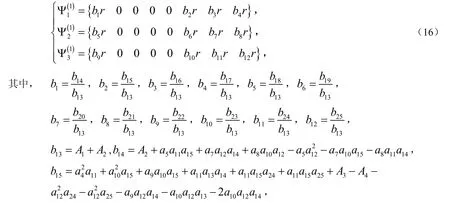
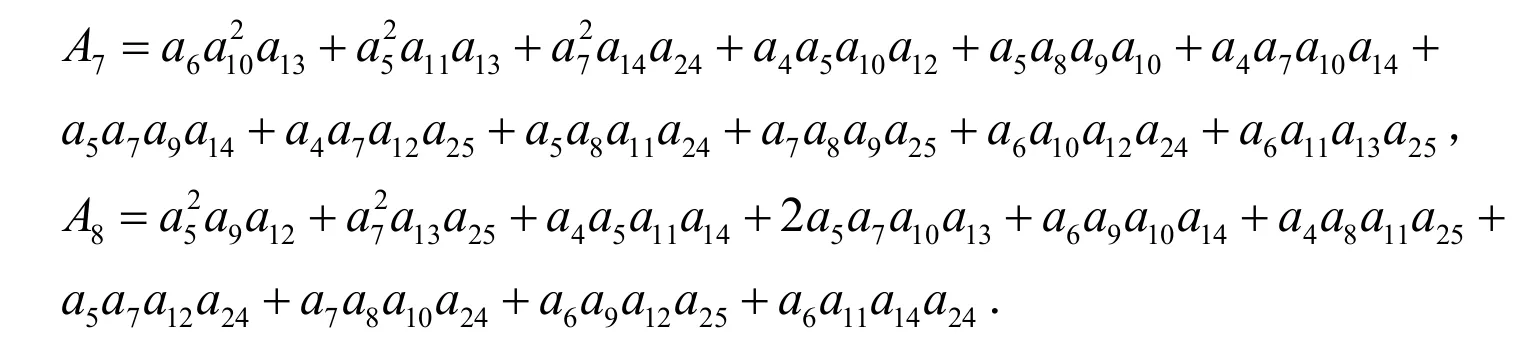
结合（14）式与（16）式，得到原问题的一阶约当型解为：

对应的物理意义分别为：均匀拉伸、均匀电场、均匀磁场．

2）二阶约当型解

二阶约当型解的控制方程为：

考虑到方程（18）的解不满足原问题的边界条件，其对应的约当型解链到此中断．

综上得到零本征值问题的所有本征解，也就是对偶方程的所有基本解向量，而它们覆盖了所有的圣维南解．

4 哈密顿体系方法的优越性

文献[6]提供了一种解析求解磁电弹性圆环板纯弯曲问题的方法，在该文献中讲到在势函数中，令D1j=0（j=1,2,3,4），可以平行推导出圆板r0=0的解析解．下面运用该方法直接给出圆板的解析解．边界条件为：

对应应力场的应力、电位移和磁感应强度分别为：

由（20）表达式看出，应力表达式与弹性力学中的表达式一样，纯弯曲问题不会引起电位移和磁感应强度的变化，但是电势和磁势却发生了变化，因此只要求解下面式（21）方程组求出C3j，再代入式（22）中即可得出位移、电势和磁势的显示表达式．

下面利用哈密顿体系方法求解文献[6]的问题．

其中η11,η12,η13为待定系数，由边界条件式（19）决定．

由（2）式及应变与应力的关系可得：

代入具体参数可以发现哈密顿体系方法和文献[6]给出的凑合法是吻合的，这两种方法最重要的区别是：哈密顿体系方法是通过给出材料所要研究问题的基本方程，导入哈密顿体系，再通过解哈密顿方程等的理性推导求得解析解；传统的凑合法则采用的是一种试探式方法，先假设出一个解，然后代入要解决的问题中，判断是否满足边界条件从而求得解析解．由此可以看出，哈密顿体系方法的优势在于它提供的是一种普通、理性的方法，并且可以满足边界条件．

[1] Van Run A M J G, Terrell D R, Scholing J H. An in situ grown eutectic magnetoelectric composite material. Part2: Physical properties [J]. J Mater Sci, 1974, 9: 1710-1714.

[2] Van Den Boomgaard J, Terrell D R, Bom R A J, et al. An in situ grown eutectic magnetoelectric composite material. Part1: Composition and unidirection solidification [J]. J Mater Sci, 1974, 9: 1705-1709.

[3] 盛宏玉. 弹性地基上自由层合圆板弯曲问题的解析解[J]. 岩土工程学报, 2000, 22(3): 323-326.

[4] 徐鹰. 弹性薄圆板混合边界问题的解析解法: 分区联合解法[J]. 南京航空航天大学学报, 1995, 27(3): 319-325.

[5] Celep Z. Circular plate on tensionless Winkler foundation1 [J]. Eng Mech Div, 1988, 114(10): 1723-1739.

[6] Nath Y. Large amplitude response of circular plates on elastic foundations1 Int [J]. Non-linear Mech, 1982, 17(4): 285-296.

[7] 陈江瑛, 侯鹏飞, 丁浩江. 磁电弹性圆环板的三个解析解[J]. 宁波大学学报: 理工版, 2002, 15(4): 8-21.

[8] 陈江瑛, 丁皓江, 侯鹏飞. 磁电弹性旋转圆环(圆盘)的三维分析[J]. 浙江大学学报: 工学版, 2003, 37(4): 440-444.

[9] 钟万勰. 弹性力学求解新体系[M]. 大连: 大连理工大学出版社, 1995: 12-19, 156-183.

Hamiltonian System Method of Orthotropic Magneto Electric-elastic Circular Plate

WANG Lina, HE Wenming
(College of Mathematics and Information science, Wenzhou University, Wenzhou, China 325035 )

Based on the Hamiltonian-system’s solving method, this paper mainly solves the problems of axial-symmetry perpendicular-anisotropy of magnetic-elastic circular-plate’s solution. The basic train of thought to solve this problem is as follows. First, the basic equations of the problem have to be guideded into the Hamiltonian-system to get the Hamiltonian-equation. Then, the Hamiltonian-equation’s zero eigen value is studied as well as its corresponding eigen solution vector. Finally, the analytic solution of the original problem is obtained. It is obvious that Hamiltonian-system method possesses the superiority compared with other solutions of solving meothods.

Orthogonal Anisotropy; Hamiltonian-system Method; Eigen Solution; Magnetoelectric-elastic Circular-plate

O24

A

1674-3563(2015)02-0019-09

10.3875/j.issn.1674-3563.2015.02.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2014-09-09

国家自然科学基金(11171257)

王莉娜(1989- )，女，山西阳泉人，硕士研究生，研究方向：计算机数学与复杂系统控制