空间分数阶扩散方程的Multiquadric拟插值解法

王自强,曹俊英,2*

(1.贵州民族大学理学院,贵州贵阳550025;2.厦门大学数学科学学院,福建厦门361005)

空间分数阶扩散方程的Multiquadric拟插值解法

王自强1,曹俊英1,2*

(1.贵州民族大学理学院,贵州贵阳550025;2.厦门大学数学科学学院,福建厦门361005)

基于拟插值算子对空间分数阶扩散方程构造了一个新的数值格式.首先在散落点上用三次Multiquadric(MQ)函数的平移构造了一个拟插值算子,分析了此拟插值算子的再生性、保形性和对分数阶导数的收敛性,最后利用上述拟插值算子并结合时间差分格式构造了空间分数阶扩散方程的计算格式.收敛性分析显示:当时间方向用Crank-Nicolson格式时,精度为O(Δt2+h4¯α),当时间方向用向后Euler格式时,精度为O(Δt+h4¯α),其中Δt为时间步长,h为空间步长.数值结果表明MQ拟插值方法是构造数值格式的一个有效工具.

Multiquadric拟插值;分数阶扩散方程;保形性;逼近性分析

由于径向基函数具有简单性、精确性、各向同性以及便于向高维问题的扩展等优点,越来越多的研究者用它们构造插值函数,得到了非常好的结果. Light[1]、Schaback等[2]分别在1992年和1996年用径向基函数来构造了一些插值函数.1971年Hardy[3]首次介绍了Multiguadric(MQ)函数.1982年Franke[4]指出:就精度、稳定性、有效性、内存要求和易于实现而言,MQ函数在29种散落数据插值格式中首屈一指.然而,当插值点数非常大时,插值矩阵可能病态.与插值相比,拟插值不但避免了病态问题,而且具有多项式再生性质和保形性质.基于拟插值方法的上述优点,研究者们如何对于非均匀数据构造出具有好性质的拟插值算子近来已经成为一个热门研究课题[5-7].由于MQ拟插值算子具有许多好性质,很多研究者开始利用MQ拟插值算子构造求解偏微分方程的数值格式[8-11].本文构造了一种MQ拟插值方法用它来求解空间分数阶扩散方程.该方法可以处理复杂的边界条件和初值具有散乱数据的情况.利用三次MQ函数的平移构造了一个高阶拟插值算子,然后将该拟插值算子用在分数阶导数上,并结合时间差分格式构造了空间分数阶扩散方程的计算格式.

1 基于MQ函数的拟插值算子的构造

假设f(x)充足光滑,我们利用MQ函数作为核函数,构造f(x)的一个拟插值算子ℜ(x),即采用函数的平移φj(x)=φ(x¯xj)作为一组基函数,其中c是形状参数且为正的常数,{(xj,为数据点,有:

其中:

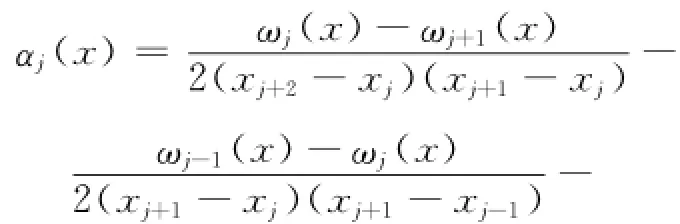
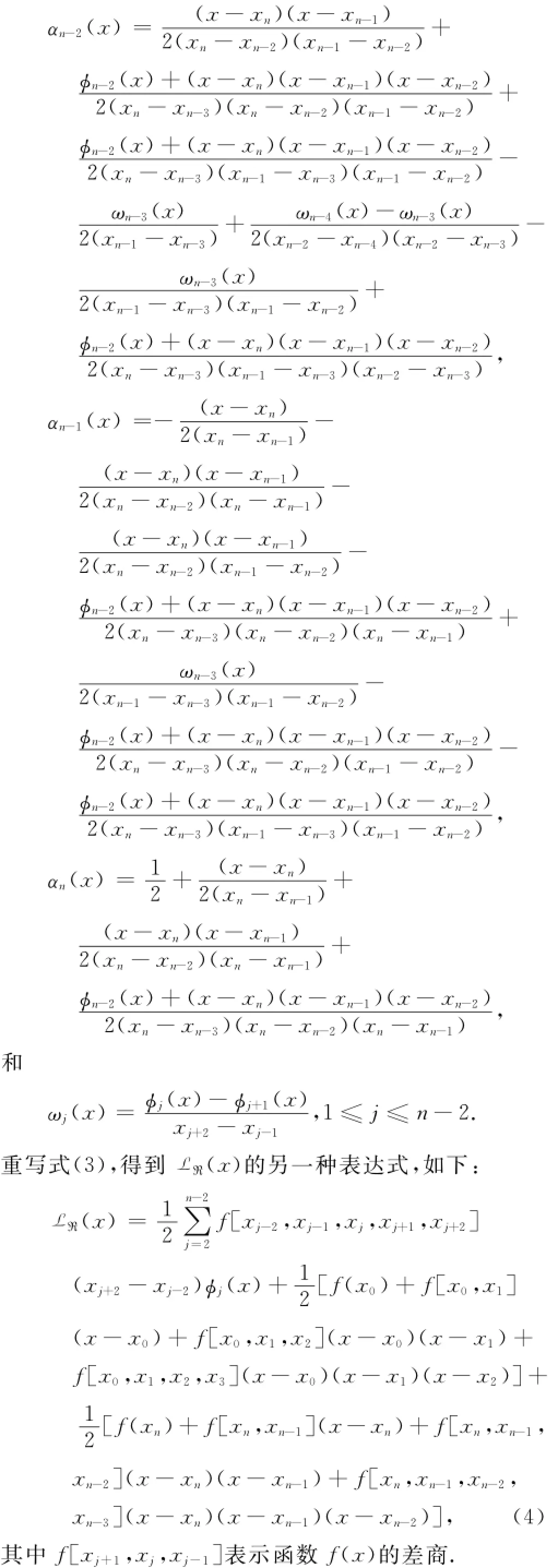
2 拟插值算子ℜ(x)的性质和逼近性

为了后面理论分析的需要,这里将引入文献[12]证明的一些拟插值算子ℜ(x)的多项式的再生性、拟凸性、三和四阶导数的凸性及其逼近性结果.

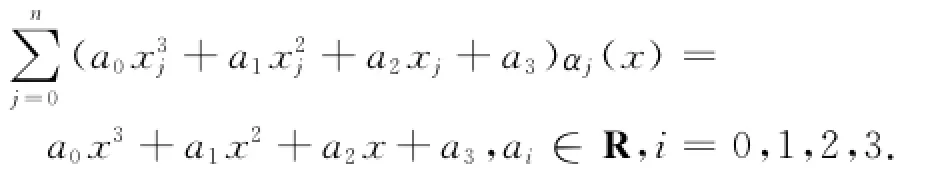
定理4 假设f(x)的三阶导数是Lipschitz连续,则当c=O(h2),拟插值算子ℜ(x)的逼近阶满足

3 基于拟插值算子的数值格式

在这里,将利用拟插值算子给出求解空间分数阶微分方程的数值格式.当1＜α＜2时,α阶Caputo导数,定义为:

定理5 设f(x)具有三阶导数Lipschitz连续,则α(1＜α＜2)阶分数阶导数的ℜ(x)满足:

证明 固定x∈[a,b],设p(y)是f(y)在点x的局部泰勒展开,亦即:

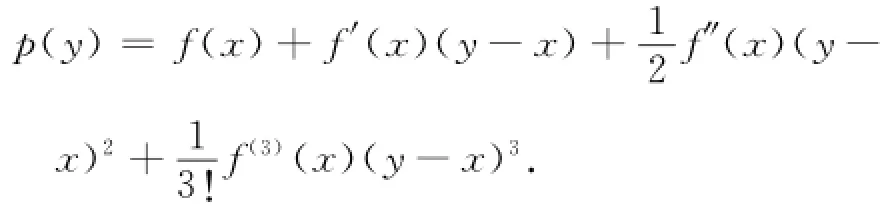
易知,p[xj¯2,xj¯1,xj,xj+1,xj+2]≡0,这里p[xj¯2,xj¯1, xj,xj+1,xj+2]表示p(y)的差商.根据定理1,得:

并且,

其中ξj∈(xj¯1,xj+2),ηj∈(xj¯2,xj+1).

引入j=0,…,n的特征函数

则有

其中Ci,i=0,1是与x和h无关的正常数.现在,我们得到了α(1＜α＜2)阶分数阶导数一个拟插值近似ℜ(x).显然,当时,收敛阶可以达到4¯α,定理证毕.

设Ω=[a,b],I=[0,T],记QT：=Ω×I,考虑如下一维的空间分数阶扩散方程(SFDEs):

满足下列初边值条件:

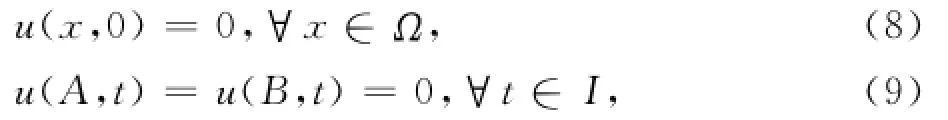
这里α∈(1,2)是空间分数阶导数的阶数.

在空间方向上,利用拟插值算子的二阶导数来逼近u″(τ,tk),因此

在时间方向上,用Crank-Nicolson格式和向后Euler格式,则有

定理6 (i)格式(10)的截断误差是O(Δt2+ h4¯α).(ii)格式(11)的截断误差是O(Δt+h4¯α).

4 数值算例

我们主要做两个方面测试,一方面,测试拟插值算子对函数的逼近性质.设f(x)=x4是被逼近函数,选择形状参数c和步长h,来测试拟插值算子ℜ(x)对被逼近函数的逼近度.在表1中,分别选取和c=0.1h,0.2h,0.5h,h,2h,计算.在表2中,分别取c=80h2,h=测试ℜ(x)当h变化时的收敛阶.为了简单起见,选择等距剖分的样点

通过分析表1的数值结果,发现拟插值算子的逼近性依赖于形状参数c和步长h.从表2中发现,当c= O(h),O(h1.5)和O(h2)时,拟插值算子ℜ(x)的收敛阶能够达到2,3和4.从图1中发现拟插值算子ℜ(x)能很好的逼近f(x).通过这些算例发现对拟插值算子数值结果和理论分析是非常吻合的.

表1 的逼近性Tab.1 The approximation capacity of

c h‖ℜ(x)¯f(x)‖∞1 10 7.105×10 1 ¯3 100 1 1 5010 7.420×10¯31 10 9.633×10¯31 1 20 10 1.763×10¯21 1 10 10 5.094×10¯21 1 5 ¯5 1 1 000100 9.846×10 1 1 100 1.028×10¯41 500 100 1.334×10¯41 1 200 100 2.425×10¯41 1 100 1 50100 6.796×10¯41 1 000 1.012×10 1 ¯6 10 000 1 1 000 1.057×10¯61 1 5 000 1 000 1.371×10¯61 1 2 000 1 000 2.493×10¯61 1 1 000 1 000 6.979×10 1 ¯6 500

表2 测的逼近阶Tab.2 The convergence order of

表2 测的逼近阶Tab.2 The convergence order of

c h‖ℜ(x)¯f(x)‖∞Rate 80 150.176 80 20 1 2 15 20 5.576×10¯24.003 3 8 1 2 1 2525 50 3.785×10¯22.015 3 65 50 1.530 81 50 50 5.036×10 1 ¯2 1.5 65 100100 6.293×10¯21 1.5 3.000 6

另一方面,测试利用拟插值算子构造的SFDEs数值格式的收敛性.考虑问题(7)～(9),其精确解为:

相应的右端项为:

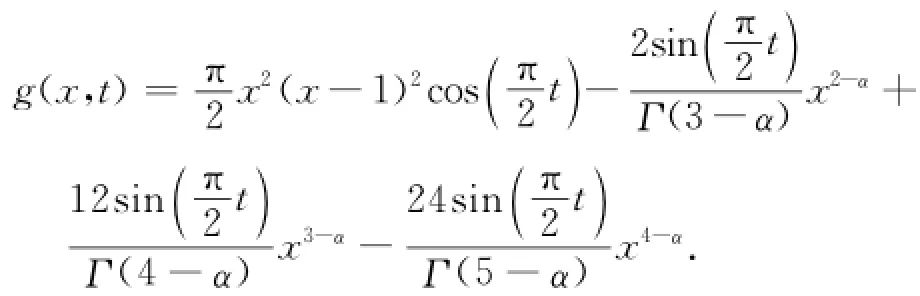
图1 取,函数f(x)=x4和它的拟插值ℜ(x)Fig.1 Function f(x)=x4and its quasiinterpolation operatorℜ(x)when

为了观察数值解逼近精确解的精度,计算了在L∞下的下面所有图和表的数值结果都是在Ω=[0,1]和T=1时得到的.

首先,研究空间方向的收敛精度.为此,取时间步长足够小使得其产生的误差不影响空间精度.表3显示了最大误差随不同的空间步长h和形状参数c的变化行为,并列出了相应的阶数.从表中看到,当1＜α＜2时,格式(10)和格式(11)的空间精度是4¯α阶.

其次,我们研究时间方向的收敛精度.表3显示了最大误差随不同的空间步长h和形状参数c的变化行为,并列出了相应的阶数.取Δt=h,从表中数据可以看出,格式(10)的时间收敛阶接近2阶.取Δt=h2,从表中发现格式(11)的时间收敛阶接近1阶.这些数值结果与理论分析相吻合.

最后,测试参数c对收敛性的影响.仅以格式(10)为例.图2表示,不同参数c下的L∞误差.从图2中发现数值解很好的逼近精确解.进一步地,我们发现当形状参数c变小时,误差也随着变小.

5 结 论

我们利用MQ拟插值方法求解空间分数阶扩散方程.首先,在散落点上利用三次MQ函数构造了一个拟插值算子,并分析了此拟插值算子的多项式再生性、保形性和对分数阶导数的收敛性.其次,利用上述插值算子并结合时间差分格式构造了分数阶扩散方程的计算格式.收敛性分析显示:当时间方向用Crank-Nicolson格式时,精度为O(Δt2+h4¯α);当时间方向用向后Euler格式时,精度为O(Δt+h4¯α).最后,数值结果表明MQ拟插值方法是构造数值格式的一个有效工具.

表3 空间和时间精度Tab.3 The spatial and temporal convergence rate of scheme

图2 ,不同参数c下的L误差∞Fig.2 The Lerrors when∞and different parameter c

[1] Light W A.Some aspects of radial basis function approximation[J].Approx Theory,Spline Functions and Applications,1992,356:163-190.

[2] Schaback R,Wu Z.Operators on radial functions[J].J Comput Appl Math,1996,73(1):257-270.

[3] Hardy R.L Multiquadric equations of topography and other irregular surfaces[J].J Geophys Res,1971,76(8): 1905-1915.

[4] Franke R.Scattered data interpolation:tests of some methods[J].Math Comput,1982,38(157):181-200.

[5] Ling L.A univariate quasi-multiquadric interpolationwith better smoothness[J].Comput Math Appl,2004,48(5/ 6):897-912.

[6] Beatson R K.Powell M J D.Univariate multiquadric approximation:quasi-interpolation to scattered data[J]. Constr Approx,1992,8(3):275-288.

[7] Zhang W,Wu Z.Some shape-preserving quasi-interpolants to non-uniformly distributed data by MQ-B-splines [J].Appl Math J Chinese Univ Ser A,2004,19(2): 191-202.

[8] Chen R,Wu Z.Solving hyperbolic conservation laws using multiquadric quasi-interpolation[J].Numer Methods Partial Differential Equations,2006,22(4):776-796.

[9] Tatari M,Dehghan M.A method for solving partial differential equations via radial basis functions:application to the heat equation[J].Eng Anal Bound Elem,2010,34(3): 206-212.

[10] Zhu C G,Wang R H.Numerical solution of Burgers′equation by cubic B-spline quasi-interpolation[J].Appl Math Comput,2009,208(1):260-272.

[11] Duan Y,Rong F.A numerical scheme for nonlinear Schrödinger equation by MQ quasi-interpolation[J].Engineering Analysis with Boundary Elements,2013,37 (1):89-94.

[12] 曹俊英.分数阶微分方程的高阶数值方法研究[D].厦门:厦门大学,2012.

Multiquadric Quasi-interpolation for Space Fractional Diffusion Equations

WANG Zi-qiang1,CAO Jun-ying1,2*
(1.College of Science,Guizhou Minzu University,Guiyang 550025,China; 2.School of Mathematical Sciences,Xiamen University,Xiamen 361005,China)

:In this article,we apply a new quasi-interpolation operator to solve the space fractional diffusion equation.We first construct a new univariate quasi-interpolation operator based on scattered points by cubic multiquadric functions.We discuss the polynomial reproduction,shape-preserving properties,and convergence for fractional derivative of this quasi-interpolation operator.Based on this quasi-interpolation,a spatial approximation is proposed to discretize partial differential equations.By combining the quasi-interpolation in space and finite difference schemes in time,we construct an efficient method to solve the space fractional diffusion equation. Numerical experiments show that the accuracy of our method is of order O(Δt2+h4¯α)if the Crank-Nicholson scheme is used,and order O(Δt+h4¯α)if Backward Euler is used,whereΔt is the time step size,and h is the space mesh size.Numerical results show that MQ quasi-interpolation method is an effective tool for constructing numerical schemes.

multiquadric quasi-interpolation;fractional diffusion equation;shape-preserving property;approximation capacity

O 241.82

A

0438-0479(2015)03-0358-06

10.6043/j.issn.0438-0479.2015.03.012

2014-03-31 录用日期:2014-08-25

国家重点基础研究发展计划(973计划)(2012(B025904));国家自然科学基金(11426074);贵州省科学技术基金([2014]2098,[2013] 2144);贵州省教育厅项目([2013]405)

*通信作者:caojunying1000@126.com

王自强,曹俊英.空间分数阶扩散方程的Multiquadric拟插值解法[J].厦门大学学报:自然科学版,2015,54(3): 358-363.

:Wang Ziqiang,Cao Junying.Multiquadric quasi-interpolation for space fractional diffusion equations[J].Journal of Xiamen University:Natural Science,2015,54(3):358-363.(in Chinese)