一种LDPC编码慢跳频系统迭代信道估计译码算法*

2015-06-23罗建，李炯

通信技术 2015年3期

关键词：错误率译码比特

罗建，李炯

(解放军理工大学通信工程学院，江苏南京 210007)

一种LDPC编码慢跳频系统迭代信道估计译码算法*

罗建，李炯

(解放军理工大学通信工程学院，江苏南京 210007)

低密度奇偶校验码(LDPC, Low Density Parity Check)的和积译码算法(SPA, Sum-product Algorithm)在加性高斯白噪声信道中具有很好的译码性能，但需要已知信道状态信息。提出了一种在部分频带干扰条件下LDPC编码慢跳频(SFH, Slow Frequency Hopping)系统的迭代信道估计译码算法。该算法利用迭代译码过程中产生的比特后验信息作为信道估计器的先验信息辅助信道估计，进而更新下一次译码的初始信息。仿真结果显示，该算法性能逼近已知信道信息时的性能，而且每跳所含的符号数很少,不需要插入导频，增大了传输功率效率。另外，相对于SPA算法运算量增加不大，实现简单。

低密度奇偶校验码和积译码算法慢跳频系统信道估计

0 引言

低密度奇偶校验码(LDPC)是一类由稀疏的校验矩阵定义的分组纠错码，由于其在采用和积译码算法(SPA)时，可以取得接近于香农极限的误码性能[1]，近年来受到广泛关注。目前国内外许多卫星跳频通信系统都采用了LDPC码编码方案作为技术标准。根据在每跳信号中是否加入导频符号，可将信道估计算法分为基于数据辅助的信道估计和基于非数据辅助的信道估计。文献[2]研究了LDPC编码慢跳频系统在BPSK相干解调时的抗部分频带干扰性能。它在每跳中加入导频符号用以信道估计。每跳中导频符号长度的选择对系统性能具有很大的影响。然而增加导频符号会降低通信系统的功率效率，减少导频符号又会降低估计精度。文献[3]在解调器和译码器之间增加一个信道估计器，它采用期望最大(EM，Expectation Maximization)算法，利用每次译码反馈的译码比特软信息得到信道估计值。这种算法具有很好的性能，在每跳包含一定数量符号的条件下与已知信道信息条件的方案性能非常接近。然而EM算法复杂度较高，不适于实际应用。文献[4]提出了一种简单的判断信道状态的干扰检测方法。该方法通过统计MFSK跳频系统中在某跳内平方率检测器输出的信号大于某门限值的个数来判决该跳是否被干扰，若个数大于某一门限值则认为该跳被干扰，否则认为该跳未被干扰。文献[5-6]研究了Turbo码慢跳频系统中的信道估计算法，并对Turbo译码算法进行了修改，在每次迭代中加入信道状态软信息的计算，而信道状态的先验信息都用前一分量译码器的输出信息代替，其估计性能也接近已知信道信息的情况，并且不需要加入导频。该方案相对于没有信道估计的系统，增加的计算量也不大，但是它需要两个分量译码器来实现信道状态与译码软信息的交互，不适于SPA译码的LDPC编码系统。文献[7]介绍了一种MPSK慢跳频系统部分频带干扰状态的判决方法。该方法先估计出每一跳内信息的方差，再用这一方差与某门限值进行比较，估计出该跳的干扰状态。由于最佳的门限值对系统参数和信道环境比较敏感，因此该方法存在一定的局限性，并且其是开环的，无法利用译码信息辅助估计。

文中对在部分频带干扰条件下的LDPC编码慢跳频系统的迭代信道估计译码算法进行了研究。提出一种将译码比特后验信息作为信道估计器的先验信息应用于信道估计中，形成一个闭环的联合信道估计译码方法。通过统计在某跳内经过干扰状态后验概率计算判决为被干扰的符号比例是否大于某一门限值来判决该跳是否被干扰，若个数大于某一门限值则认为该跳被干扰，否则认为该跳未被干扰。该方案无需插入导频，且具有接近已知信道状态方案的性能，相对于SPA算法增加的计算量也不大，易于实现。

1 LDPC编码慢跳频通信系统模型

在发送端输入信息经LDPC编码后依次进入调制器和跳频器，而后进入信道，并假设每跳的信息所经历的信道状态相同，即每跳全被干扰或全部未被干扰。在接收端，经解跳解调(假设已准确解跳同步)后输出的信号为

y=x+n0+nJ

(1)

式中,x表示调制后的符号；n0表示加性高斯白噪声信号；nJ表示部分频带干扰信号。解调信息y的概率密度函数为

(2)

(3)

式中,z=0表示未被干扰；z=1表示被干扰。和积译码器根据信道传递的初始信息进行译码，每次迭代计算得到信息比特软信息，将其作为信道估计所需的比特先验信息传输至信道估计器进行辅助信道估计。系统框图如图1所示。假设码组长度为N，每跳Nh个符号，则传输一个码组需要N/Nh跳。

2 迭代信道估计译码算法

LDPC码的译码算法是一种迭代算法，在初始时刻所有变量节点接收编码信道概率信息，而后开始迭代译码计算。迭代过程中，校验节点和变量节点之间相互交换信息。首先，每个变量节点将其可靠信息传送给每个与之相连的校验节点，这个可靠信息就是编码信道概率信息。然后，每个校验节点处理其得到的可靠信息，并将其传送给每个与之相连的变量节点，完成信息的一次交互。随后变量节点和校验节点依次处理对方获得的可靠信息并传递给对方，如此往复，经多次迭代达到译码迭代停止条件后，译码结束，输出译码结果。其原理图如图2所示。

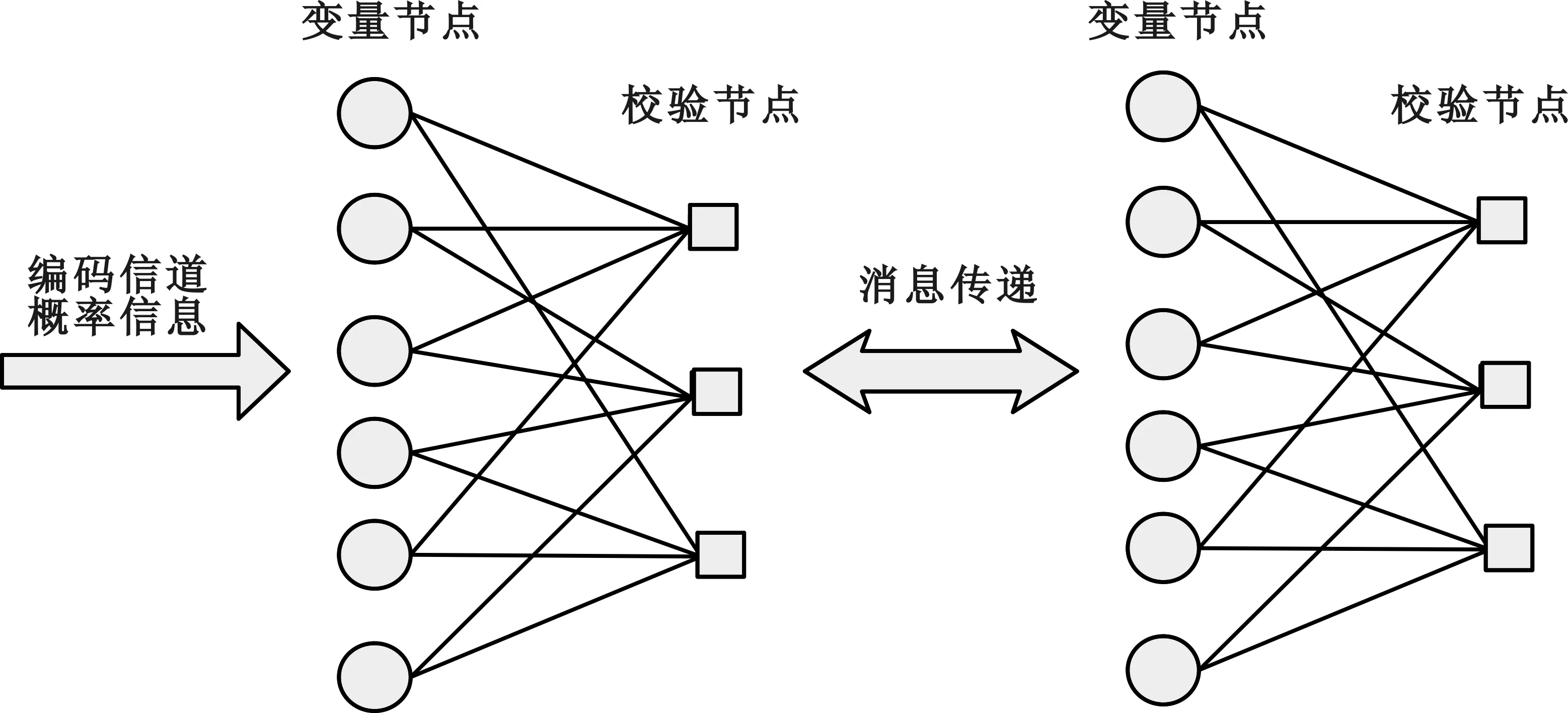
图2 LDPC译码算法原理

译码过程中需要使用外部信道信息的有两处，分别是译码信道概率信息初始化和变量节点的更新。由此可知信道概率信息始终贯穿于译码过程。文中提出一种利用每次译码迭代得到的比特软信息进行辅助信道估计的算法，用以更新译码初始化信息。更新规则如下：

由贝叶斯定理得第l次迭代第j跳第i个符号所受干扰状态的后验概率为

(4)

式中,j=1,2,3…N/Nh;i=1,2,3…Nh;p(l-1)(xji)表示第j跳第i个比特在第l-1次译码过程得到的后验概率。用下式判决该跳是否受到恶意干扰

(5)

式中

(6)

(7)

γ(0≤γ≤1)为门限因子；ρ为干扰因子。

根据判决结果即可对译码初始信息进行更新，具体操作如下

(8)

(9)

在变量节点进行更新操作时，将更新后的信道概率信息作为译码初始信息加入计算过程。由于每次迭代译码过程所得的比特信息可靠性不断增高，信道估计器用此软信息作为先验符号信息所得的符号干扰状态信息似然函数(式(4))的准确度也越来越高。在进行干扰状态判决时(式(7)、式(5))，可靠性也随之增高。

3 仿真分析

文中对LDPC编码慢跳频系统的迭代信道估计译码算法进行了仿真，仿真分析了门限因子γ以及每跳符号数对干扰检测错误率(漏检和虚警概率)和系统误码率的影响。仿真中使用码长为1 104，码率1/2，行重为3，列重为6的规则LDPC码。信源等概率分布。其中“SI”代表已知干扰状态信息，干扰状态的概率P(z=1)=ρ，P(z=0)=1-ρ。比特信噪比Eb/N0=20 dB，干扰因子ρ=0.6。

门限因子的选择对干扰检测判决的成功与否具有很大的影响。干扰因子取值过大，会产生误判，使受干扰的信号误判为未受干扰；干扰因子取值过小会使未受干扰的信号误判为受到干扰，进而影响译码初始信息的更新。图3和图4分别比较了在不同门限因子条件下干扰检测判决错误概率曲线和误码性能曲线。由图可以看出门限因子取值过大或过小均会产生较大的错误判决率和误码率。

图3 不同判决因子对干扰检测判决的影响(Nh=12，SJR=2 dB，4 000次独立仿真)

图5给出了每跳12个符号，门限因子取0.3，4 000次独立仿真，不同信干比条件下干扰检测判决错误率随译码迭代次数的变化曲线。第一次迭代处理时，比特先验信息设为等概率分布，首次判决的主要因素是似然函数的比值。在低信干比条件下似然函数在有无干扰时的差距较大，判决更为准确。在后续的迭代处理过程中，引入了译码比特软信息作为信道估计器的比特先验信息来计算符号受干扰状态后验概率(式(4))，由于随着迭代次数的增加，译码比特信息的可靠性也在增高，使得式(4)的计算更为可靠。干扰检测错误率会逐渐收敛至一个较小值，且信干比越高其收敛速度越快。

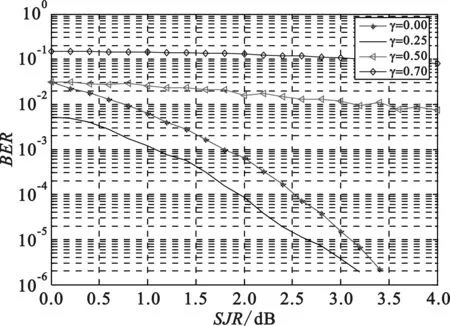
图4 不同判决因子对误码性能的影响(Nh=12)

由于低信干比时译码错误率较高，在计算时会受到影响，导致在判决干扰状态时出现错误(虚警或漏检)。随着信干比的增高似然函数在有无干扰时的差距逐渐减小，但译码信息可靠性在不断增高，能够有效修正判决结果。故而在似然函数差距和译码正确率之间有一个折中。所以图5中没有出现判决错误率随信干比增高逐渐变大或减小的趋势。

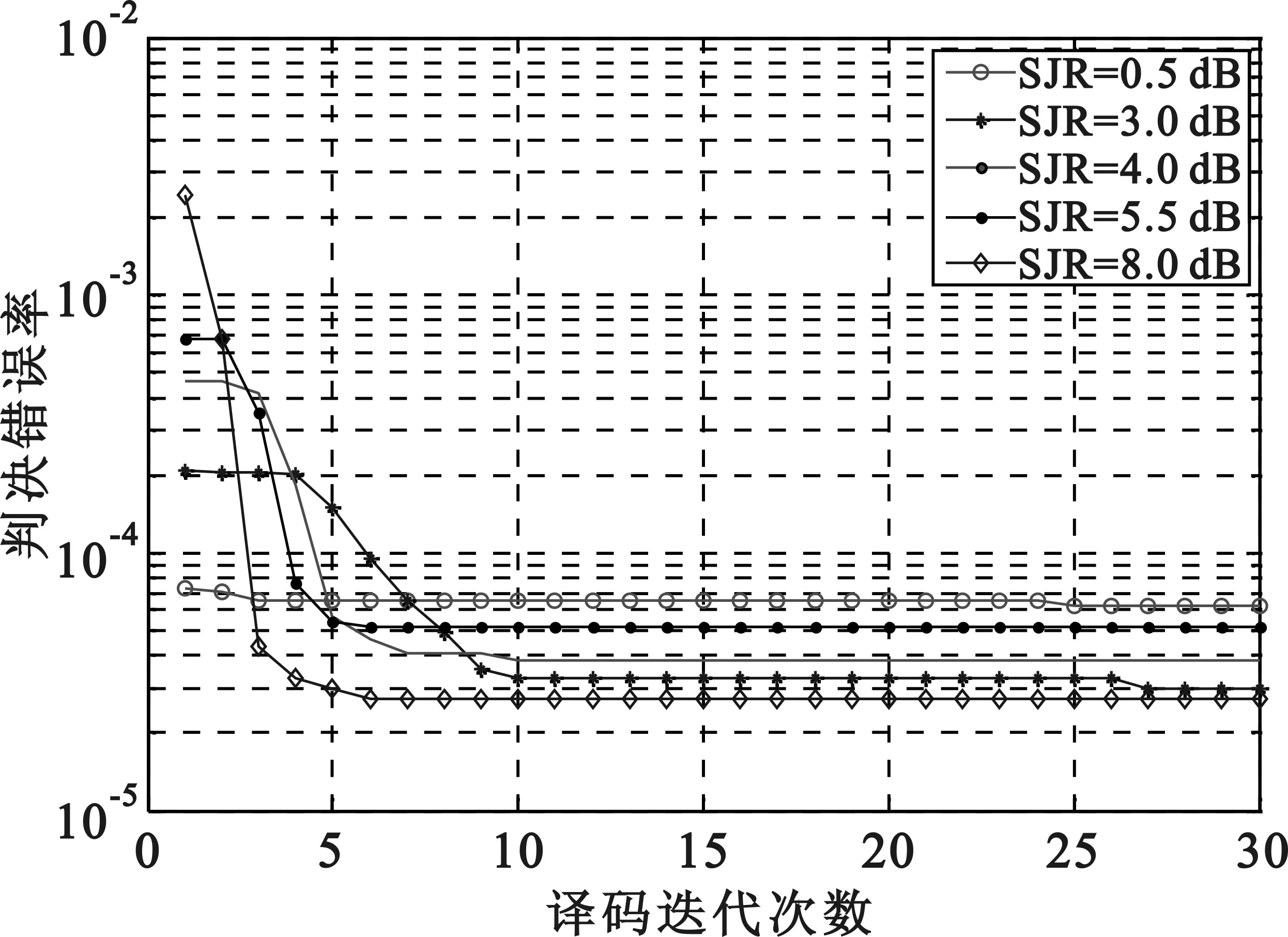
图5 不同信干比对干扰检测判决的影响

由式(5)可知文中提出的迭代信道估计译码算法是利用了基于统计的干扰检测判决方法。因此，每跳所含的符号数也是本算法所要考查的一个关键参数。图6给出了每跳不同符号数条件下干扰检测判决错误率随迭代次数变化曲线。由图6可以看出随着每跳符号数的增加判决错误率在减小，在每跳16个符号时译码第6次迭代判决错误率已达到一个很低的值。这说明每跳符号数越多统计越准确，干扰检测判决正确率越高。

图6 每跳不同符号数对干扰检测判决的影响(γ=0.25，SJR=2 dB，4 000次独立仿真)

图7比较了每跳不同符号数时采用文中提出算法的系统的误码性能，由图7中可以看出采用文中所提出的译码算法的编码慢跳频系统并不像传统跳频系统中那样每跳传输的符号数越少越好[8]。这主要是因为虽然每跳的符号数少时受干扰的符号数较少，但此时干扰检测错误率较高，因此在每跳符号数较少时误码率性能较差。采用文中算法与已知信道干扰状态信息相比较，每跳8个符号在误码率为10-4时，信干比相差2.5 dB左右。

图7 每跳不同符号数对误码性能影响(γ=0.25)

随着符号数的增加干扰检测判决正确率增高，误码性能逐渐逼近已知干扰状态信息条件下的性能。在每跳符号数增加到一定值时，误码率性能仍会以每跳传输的符号数的增加而减小这一规律出现。文中在每跳12个符号时误码性能已非常逼近已知状态信息条件下的性能。

4 结语

LDPC码的SPA译码算法具有很好的抗噪声性能，在加性高斯白噪声信道中具有能够逼近香农极限的特点，但是该算法对译码过程的初始信息非常敏感，需要知道当前的信道状态。文中研究了一种在部分频带干扰条件下的LDPC编码慢跳频系统的迭代信道估计译码算法。该算法将迭代译码过程中所产生的译码比特软信息反馈回信道估计器，作为发送比特先验信息重新辅助判决干扰状态信息，得到的干扰状态信息用以更新下一次迭代译码的初始信息。信道估计与译码交替进行，随着译码迭代次数的增加信道干扰状态趋于已知。该方法性能逼近已知信道信息的方案，且每跳所需的符号数较少。另外，该算法相对于SPA译码算法所增加的复杂度并不高，且不需要知道信道状态信息，故实现简单。

[1] MacKay D J C and Neal R M. Near Shannon Limit Performance of Low Density Parity Check Codes [J]. Electronics Letters, 1996, 32(18): 1645-1646.

[2] Andrew W, Wayne S. Interference Mitigation Frequency Hopped Spread-Spectrum Systems[C]// IEEE 6th International Symposium on Spread Spectrum Techniques and Applications. Beijing: IEEE, 2000:58-62.

[3] Torrieri D, Cheng S and Valenti M. C. Robust Frequency Hopping for Interference and Fading Channels [J]. IEEE Transaction on Communications, 2008, 56(8):1343-1351.

[4] ZHOU Z Q, LI S Q and CHENG Y F. Generation of Side Information for Fast Frequency Hopping in Partial-Band Jamming[C]// WiCOM 2010. Chengdu ,China: ISSN, 2010:23-25.

[5] KANG J H, Stark W. E. Turbo Codes for Non-Coherent FH-SS with Partial Band Interference [J]. IEEE Transaction on Communications,1998,46(11):1451-1458.

[6] 吴团峰，杨喜根.Turbo 编码GMSK信号准相干解调时的迭代信道估计和译码研究[J].通信技术，2006，27(07):23-28. WU Tuan-feng，YANG Xi-gen. Iterative Channel Estimation and Decoding Algorithm for Quasi-Coherent Demodulation of Turbo Coded GMSK Signals[J]. Communications Technology. 2006, 27(07),23-28.

[7] Philippe SEHIER, Pascal BRELIVET, Isab- lelle AUBRY. A New Jammer Estimation Method Adapted to FH-PSK Waveforms[C]// IEEE Military Communications Conference.1994. MILCOM’94. Boston, MA, USA: IEEE, 1994:1027-1031.

[8] GONG Chao, ZHANG Ying-xian, ZHANG Bang-ning, GUO Dao-xing. Performance of LDPC Coded SFH System with Partial-Band Interference[C]// ICWCA 2011. Sanya, China:Springer, 2012:145-155.

LUO Jian(1990-)，male，graduate student，majoring in communication anti-jamming.

李炯(1988—)，男，博士研究生，主要研究方向为无线通信和抗干扰。

LI Jiong(1988-)，male，doctoral postgraduate，mainly engaged in wireless communications and anti-jamming.

A Decoding Algorithm with Iterative Channel Estimation in LDPC Coded SFH System

LUO Jian, LI Jiong

(1.College of Communication Engineering, PLA University of Science and Technology, Nanjing Jiangsu 210007, China)

LDPC (Low Density Parity Check) code and SPA (Sum-Product Algorithm) both enjoy excellent decoding performance in AWGN (Additive White Gaussian Noise) channels, and however, channel state information is required. In this paper, a decoding algorithm with iterative channel estimation and partial band jamming in LDPC coded SFH system is proposed.In this algorithm,the bit posteriori information obtained from iterative decoding process is used as the assitant apriori information of channel estimator, and then updating the initial information in the next iteration process is updated. Simulation results indicate that the performance of the proposed algorithm is quite close to that of the algorithms with perfect estimation of channel-state information. What’s more, only a few symbols per hop are needed and no pilot carrier is required in this algorithm, thus it improves the efficiency of transmission power is improved. In addition, this algorithm is similar to the SPA algorithm in complexity, and therefore is easy to implement.

LDPC; SPA; slow frequency-hopping system; channel estimation

date:2014-10-10；Revised date：2015-02-06

TN92

1002-0802(2015)03-0306-05