一种混合混沌序列的研究*
2015-06-23张严平陆锐敏马世旺
张严平,陆锐敏,马世旺
(1. 解放军理工大学 通信工程学院,江苏 南京 210007;2. 南京电讯技术研究所,江苏 南京 210007)
一种混合混沌序列的研究*
张严平1,陆锐敏2,马世旺1
(1. 解放军理工大学 通信工程学院,江苏 南京 210007;2. 南京电讯技术研究所,江苏 南京 210007)
针对单一混沌映射产生的序列复杂度比较低的缺点,提出一种新的混合混沌序列产生方法。该方法主要是通过组合不同的混沌映射并且扰动混沌映射中的参数来产生混沌序列。对产生的序列进行了平衡性、随机性和相关性等分析,并将该序列作为扩频码用于直接序列扩频系统中进行仿真。仿真结果表明,这种混合混沌序列有较好的平衡性、随机性和相关性,证明了该序列作为扩频码的可行性。
混沌序列 改进型Logistic映射 Chebyshev映射 直接序列扩频
0 引 言
直接序列扩频通信系统由于其良好的抗干扰、多址、保密等性能已被广泛应用于通信、测控和导航等领域,是目前运用最为广泛的一种扩频通信系统。在直扩系统中,扩频码的选择直接影响到直扩系统的性能好坏,所以对于扩频码的研究一直是个热点。随着直扩技术的不断发展和需求的增加,传统的扩频码如m序列和Gold码因为其周期不长、数量有限等缺点已经无法满足大容量直扩系统的要求。而混沌序列可以产生大量且相关性良好的序列,因此近年来越来越受到重视。
目前,大部分的混沌序列主要是基于单一的混沌映射产生的,比较常见的混沌映射有Logistic映射、改进型Logistic映射[1]、Chebyshevy映射[2]和Tent映射。由此产生的混沌序列虽然实现比较简单,平衡性和相关性比较良好,可以作为扩频码应用于直接序列扩频系统之中,但是随着混沌理论研究的不断深入,基于单一混沌映射产生的混沌序列复杂度较低的缺点逐步显现出来。而在军事扩频通信中,复杂度低的序列容易被破解,所以复杂度高的序列具有较大的意义[3]。本文提出了一种将改进型Logistic映射和Chebyshevy映射组合并且通过改进型Logistic映射来扰动Chebyshevy映射参数的方法来产生混合混沌序列,这种方法提高了序列的复杂度,降低了被破解的可能性,同时该方法产生的序列平衡性、随机性和相关性等各项性能良好。
1 混合混沌序列的产生
1.1 改进型Logistic映射和Chebyshevy映射
改进型Logistic映射的表达式[1]为
(1)
式中,参数u的取值范围为[0,2],一般取2,当-1≤xn≤1时,映射会处于混沌状态,其概率密度函数[1]为
(2)
w阶的Chebyshevy映射的表达式[2]为
(3)
式中,当参数w≥2时,映射处于混沌状态,其概率密度函数[2]为:
(4)
改进型Logistic映射和Chebyshevy映射都是传统的一维混沌映射,由此产生的序列都有比较优良的性能,所以通过改进型Logistic映射和Chebyshevy映射的组合来构造混合混沌的模型。
1.2 混合混沌的模型
如图1所示,该混合混沌模型主要是由一个改进型Logistic映射和两个Chebyshevy映射组合而成,产生混合混沌序列的步骤如下:
1)改进型Logistic映射产生序列f1,通过f1来扰动Chebyshevy映射1中参数w,即w=4+f1。
2)Chebyshevy映射1产生序列,并二值量化为序列f2。
3)Chebyshevy映射2中参数设为4,即w=4,产生序列并二值量化为序列f3。
4)将序列f2和序列f3进行异或产生混合混沌序列f3。
通过以上步骤,可以产生混合混沌序列。
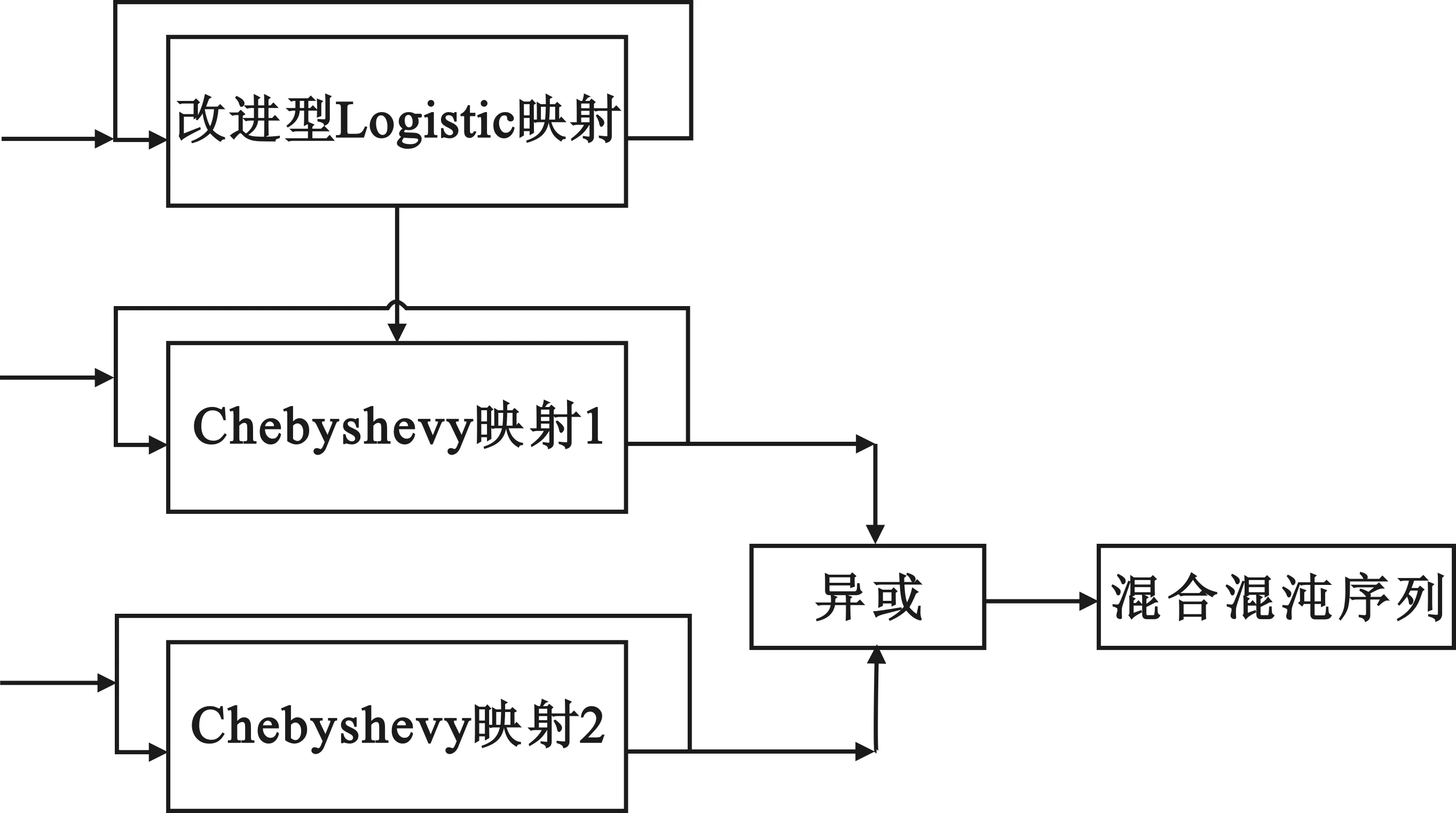
图1 混合混沌的模型
2 混合混沌序列的性能分析
2.1 初值敏感性分析
初值敏感性是混沌系统的一个很重要的特性,它是指混沌映射的初值即使存在很小的差异产生序列之间的差异也会随着迭代次数而呈指数增长,虽然产生的序列是由初始值和迭代函数所决定的,但是随着迭代次数的增加,所得的混沌序列与伪随机序列没有差别。
根据上文所述的混合混沌序列的产生方法,可以步骤2)中的Chebyshevy映射1产生的序列的初值敏感性来表征整个系统的初值敏感性。取初值分别为0.200 00和0.200 01,如图2所示为改进型Logistic映射的初值敏感性,图3所示为混合混沌的初值敏感性。从图2,图3中可以看出改进型Logistic映射在迭代十几次之后才能出现差异,而混合混沌序列在迭代七次就出现差异,说明混合混沌序列具有较为良好的初值敏感性和更大的初值空间。
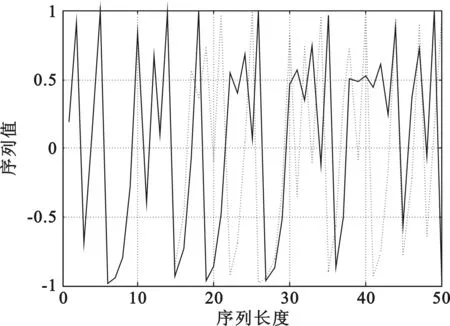
图2 改进型Logistic映射的初值敏感性
2.2 随机性分析
序列的随机性能是一个非常重要的特性,在直接序列扩频通信系统中,序列随机性能决定了系统的信息安全性能,序列随机性能越好,越接近于理想伪随机序列,系统的信息安全性就越高。因此对混合混沌序列进行随机性分析是非常有必要的。
本文对混合混沌序列进行随机性分析采用的是FIPS PUB 140-2标准[4],该标准的主要内容如下:
选取一个连续20 000比特长的0-1序列进行四项测试:
1)单位测试:统计这20 000比特长的序列中1的个数,个数应在9 725~10 275之间。
2)扑克测试:将这20 000比特长的序列分为5 000段,每段为4个比特序列,共有16种情况,统计这16种情况出现的次数x,然后计算f
(5)
f应在2.16~46.17之间。
3)游程测试:统计这20 000比特长的序列中所有长度的1的游程,应在表1所示的范围内。
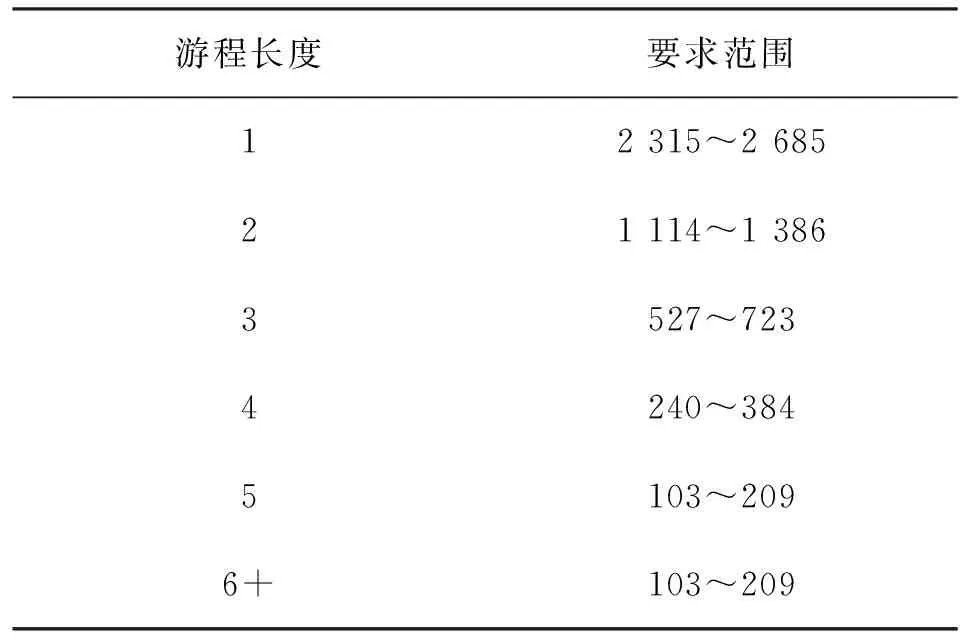
表1 游程测试规范
4)长游程测试:这20 000比特长的序列中没有长度超过25的游程。
表2为任意五组的混合混沌序列随机性测试结果,表3为任意五组4阶的Chebyshevy映射产生的序列随机性测试结果,由表2、表3可以看出,混合混沌序列在单位测试中表现出来的性能更加优良,扑克测试和游程测试性能则差不多,由此可以证明混合混沌序列具有良好的随机性。
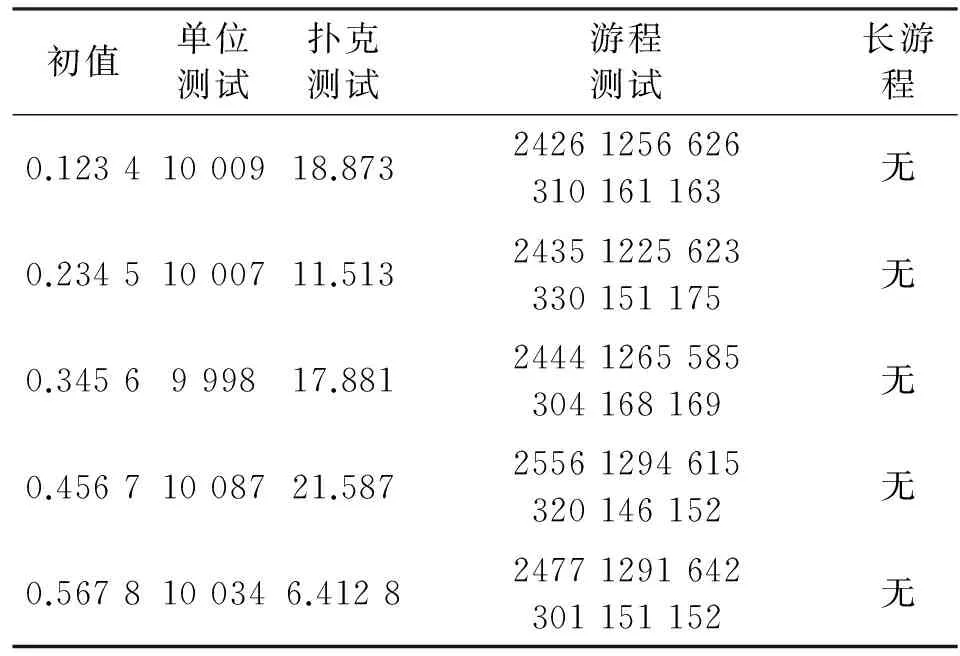
表2 测试结果
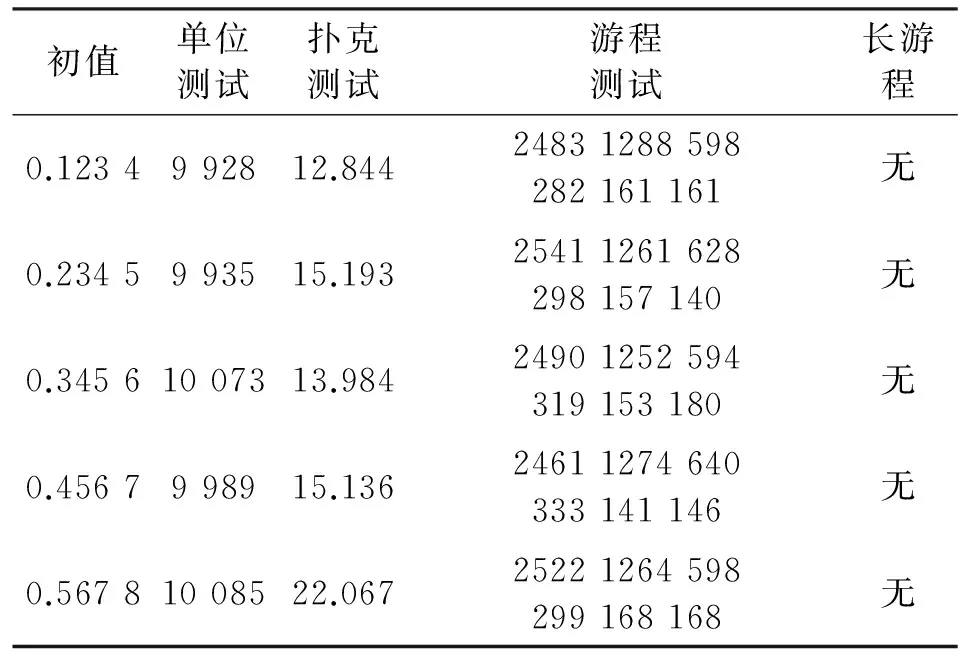
表3 测试结果
2.3 平衡性分析
在直接序列扩频通信系统中应选择平衡性较好的序列,因为序列的平衡性和载波抑制度有密切联系,平衡性差的序列会导致载波泄露,容易导致信息暴露,被截获、破解。
将混合混沌序列中0,1的个数分别用X,Y来表示,则序列的平衡度可以表示为
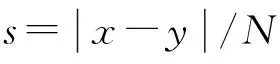
(6)
如图4所示,混合混沌序列的平衡度小于改进型Logistic映射产生序列的平衡度,并且随着序列长度的增加,混合混沌序列的平衡度逐步趋于0,这说明混合混沌序列具有良好的平衡性。
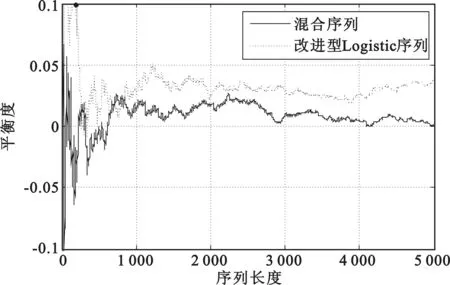
图4 平衡性
2.4 相关性分析
在直接序列扩频通信系统中,具有良好的相关特性的扩频码是至关重要的,对于直扩通信的性能具有决定性作用[5],自相关值需近似于δ函数,以利于扩频码的检测与同步,而互相关值需接近于0,以有效地抑制不同扩频码之间的干扰,这对直扩系统的多址应用十分重要。
如图5所示为取初值为0.200 00,序列长度为3 000时混合混沌序列的自相关值,图6所示为取初值为0.200 00与0.200 01,序列长度为3 000时混合混沌序列的互相关值。
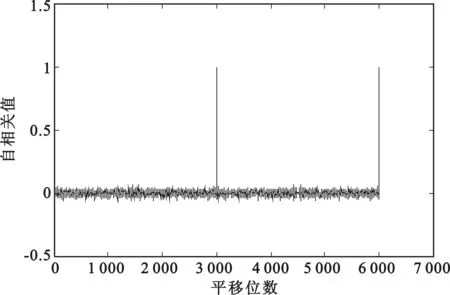
图5 自相关值
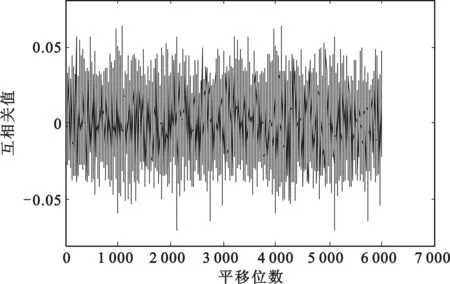
图6 互相关值
由图5、图6可知,混合混沌序列具有比较理想的自相关和互相关特性,符合作为扩频码在相关性特性方面的要求。
3 直接序列扩频通信应用仿真
为了进一步说明混合混沌序列作为扩频码的可行性,建立了直接序列扩频通信系统来进行误码率的仿真,其原理如图7所示。在此系统中,取扩频倍数为10,采用BPSK的调制和解调方式,信道为高斯白噪声信道,并与改进型Logistic映射产生的序列的误码率进行对比。
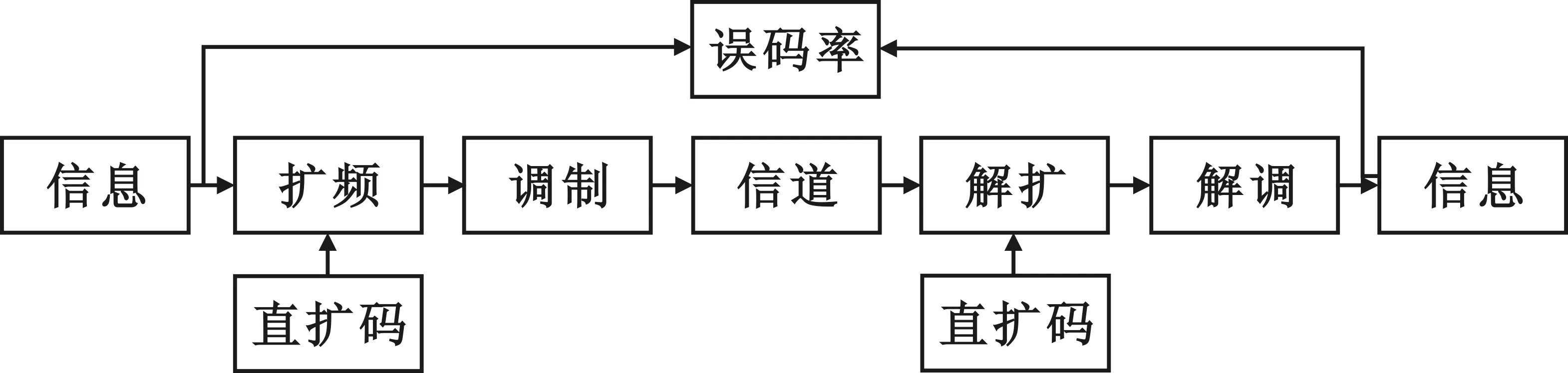
图7 直接序列扩频通信系统框
如图8所示为混合混沌序列和改进型Logistic映射产生的序列作为扩频码的误码率曲线图。
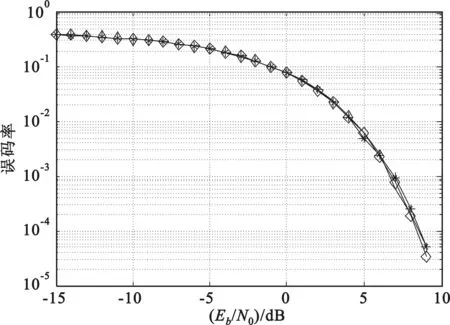
图8 误码率仿真
从图8中可以看出,混合混沌序列和改进型Logistic映射产生的序列具有差不多的误码率特性,且与理论值[6]相近,但与由于混沌序列的数目众多,可以进行优选来达到更好的效果[7]。
4 结 语
基于单一的混沌映射产生的序列虽然实现比较简单,平衡性和相关性比较良好,但由于复杂度低等缺点用于直接序列扩频通信方面会有被破解的风险。本文提出的混合混沌序列通过两种单一混沌映射的组合,与基于单一混沌映射产生的序列相比有效地提高了复杂度和保密性,并且混合混沌序列具有良好的平衡性、随机性和相关性等性质,可以满足作为扩频码的各项特性要求,是一种很有应用前景的扩频序列。
[1] 王亥,胡键栋.改进型Logistic-Map混沌扩频序列[J].通信学报,1997,8(08):71-77. WANG Hai, HU Jian-dong.The Improved Logistic-Map Chaotic Spread-Spectrum Sequences [J].Journal of China Institute of Communications, 1997,8(08):71-77.
[2] 雷利华,马冠一,蔡晓静等.基于Chebyshevy映射的混沌序列研究 [J].计算机工程,2009,12(24):4-6. LEI Li-hua, MA Guan-yi, CAI Xiao-jing, SHI Hu-li. Study of Chaotic Sequence based On Chebyshev Map [J]. Computer Engineering, 2009, 12(24):4-6.
[3] 黄乘顺,李星亮. 基于混沌的扩频通信系统及性能分析[J].通信技术,2008,41(12):37-39. HUANG Cheng-shun, LI Xing-liang. Spread-Spectrum Communication System and Its Performance Analysis based on Chaos [J].Communications Technology, 2008,41(12): 37-39.
[4] National Institute of Standards and Technology, FIPS PUB 140-2:Security Requirements for Cryptographic Modules[S]. Federal Information Processing Standards Publication,2001.
[5] 张邦宁,魏安全,郭道省. 通信抗干扰技术[M].北京:机械工业出版社,2006:63-64. ZHANG Bang-ning, WEI An-quan, GUO Dao-sheng. Anti-jamming Technologies of Communication [M]. Beijing: China Machine Press, 2006:63-64.
[6] 樊昌信,曹丽娜. 通信原理[M].北京:国防工业出版社,2007:206-207. FAN Chang-xin,CAO Li-na. Principles of Communications[M]. Beijing: National Defence Industry Press, 2007:206-207.
[7] 刘利,张建东,郑志军. 混沌扩频通信系统仿真[J]. 舰船电子工程,2010,10(30):75-77. LIU Li, ZHANG Jian-dong, ZHENG Zhi-jun. Simulation of Chaotic Spread Spectrum Communication System [J]. Ship Electronic Engineering,2010,10(30):75-77.
ZHANG Yan-ping, (1990-),male, M.Sci., majoring in satellite communication and spectrum spreading.
陆锐敏(1963—),男,研究员,主要研究方向为卫星通信;
LU Rui-min(1963-),male, research fellow, majoring in satellite communication.
马世旺(1989—),男,硕士,主要研究方向为卫星通信。
MA Shi-wang(1989-),male, M.Sci., majoring in satellite communication.
Discussion on Mixed Chaotic Sequence
ZHANG Yan-ping1, LU Rui-min2, MA Shi-wang1
(1.Institute of Communication Engineering, PLA University of Science & Technology,Nanjing Jiangsu 210007,China;2.Nanjing Telecommunication Technology Institute, Nanjing Jiangsu 210007,China)
Due to the deficiency of low sequence complexity generated by single chaotic mapping, a novel production method of mixed chaotic sequence is proposed. The mixed chaotic sequence is produced by combining different chaotic mappings and changing the parameter of chaotic mapping. Balance, randomness and correlation of the mixed chaotic sequence are analyzed, and this sequence, taken as spreading code, is simulated in direct sequence spreading system. Simulation result shows that this mixed chaotic sequence enjoys higher balance, better randomness and excellent correlation, and further verifies that this sequence could be taken as spreading code.
chaotic sequence; modified Logistic mapping; Chebyshev mapping; DSSS
date:2014-09-21;Revised date:2015-01-15
TN918
A
1002-0802(2015)03-0267-05

张严平(1990—),男,硕士,主要研究方向为卫星通信、扩频通信;
10.3969/j.issn.1002-0802.2015.03.005
2014-09-21;
2015-01-15
