公路隧道正台阶法施工错距优化及二衬支护时机优化
2015-06-21周亚鸿易秋娟
周亚鸿,易秋娟
(湖南省湘筑工程有限公司)
公路隧道正台阶法施工错距优化及二衬支护时机优化
周亚鸿,易秋娟
(湖南省湘筑工程有限公司)
隧道及地下空间工程给人们带来方便,但是,隧道在施工和运营过程中也出现了一些问题,特别是在浅埋等较差的工程地质条件下,问题尤为突出。为了更好地掌握隧道浅埋段的动态变形,及时反馈指导现场施工,优化支护结构,对公路隧道正台阶法施工错距优化及二衬支护时机优化进行分析。
隧道;数值模拟;二衬支护
1 工程概况
D隧道为双向分离式4车道公路隧道,行车速度设计值为50 km/h。左洞起止里程:ZK4+514~ZK5+062,长8 m,起止点高程分别为776.27 m、769.57 m;右洞起止里程:YK4 +498~YK5+053,长555 m,起止点高程分别为775.99 m、767.67 m。隧道为直线单向纵坡隧道,隧道左洞的坡度设计值是-1.22%,隧道右洞的坡度设计是-1.5%。隧道左线埋深最大值约为86 m,右线埋深最大约为87 m。洞身有存在几处埋深比较浅工段,最小埋深约为14 m。
2 上下台阶施工错距优化
2.1 数值模拟结果
在只考虑隧道开挖初期上下台阶错距对隧道稳定性造成的即时影响的情况下,文章选取12种不同的上下台阶施工错距,并应用FLAC3D对这12种工况模拟分析。通过研究,确定隧道围岩沉降与上、下台阶之间不同施工间距的关系。隧道拱顶沉降曲线,如图1所示。地表的最大沉降曲线,如图2所示。同样釆取12种不同的开挖错距施工时,隧道上台阶与下台阶之间不同施工间距对隧道围岩沉降的影响情况,见表1。
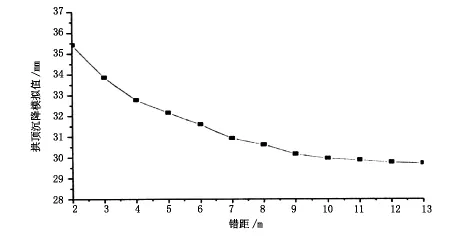
图1 拱顶沉降曲线
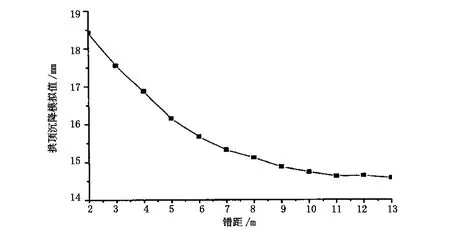
图2 随道地表沉降曲线

表1 不同错距随道变形值
2.2 数值模拟结果分析
根据图1、图2、表1可以得出以下结论。
(1)不同的上台阶与下台阶施工错距可能会导致不同的隧道变形量;随着上台阶与下台阶之间施工错距的增大,隧道围岩位移受影响程度变小,最后基本上不再发生变化。
(2)随上下台阶施工错距的增加,拱顶沉降量随时间累积而增大,而变形速率逐渐减小;上、下台阶施工错开距离从2 m增加到9 m的时候,即上下台阶错距增加了7 m的时候,隧道拱顶沉降最大数值从2 m时的35.42 mm减小到9 m时的30.16 mm,减小了5.26 mm(见表1);而施工错升距离从9 m增加到13 m时,即错距增加了4 m时,拱顶最大沉降量由9 m时的30.16 mm减小到13 m时的29.71 mm,洞顶沉降仅仅减小了0.45 mm;说明当上、下台阶施工错开距离大于9 m时,尽管上、下台阶错距增大,隧道拱顶沉降几乎不再发生变化。
(3)分析隧道地表沉降曲线,图2得出,地表沉降速率和影响程度伴随着隧道上台阶与下台阶掌子面施工错距的变大而渐渐变小。上台阶与下台阶掌子面施工错距大于10 m时,地表沉降基本上不再发生变化;掌子面错距从2 m增大到l0 m时,地表的沉降值增大了3.69 mm;而掌子面错距从10 m增大到13 m时,隧道顶部地表的沉降值增大了0.16 mm。这表明,施工错距大于10 m后地表沉降值只会发生很小的变化。
(4)掌子面错距大于10 m后,不能依靠扩大上下台阶掌子面的间距控制隧道拱顶以及隧道上方地表的沉降,追根究底,考虑到空间效应的情况下,上台阶与下台阶之间掌子面错开间距很大时,上台阶幵挖对下台阶幵挖产生的叠加效应非常小,上、下台阶开挖时相互之间产生的影响变小,控制围岩沉降变形已经几乎不再受到上台阶与下台阶之间的错距的影响。
(5)上台阶与下台阶之间的施工错距合理范围建议取值10~12 m。
3 二衬支护时机优化
3.1 变形速率准则
变形速率准则:根据《公路隧道施工技术规范》(GTGF60-2009)规定,当拱顶下沉〈0.07~0.15 mm/d,隧道适合施作二衬支护。隧道初期支护后,隧道岩土体的形变量随时间而逐渐变大,经过一定的时间,当时间为tl时刻,隧道变形量趋于某一定值yl;此后,随时间推移,变形速率减小,直至变形速率趋于零,拱顶的变形速率基本稳定在0.07~0.15 mm/d范围内,根据变形速率准则可以确定tl时刻为二次衬棚支护时机。以YK4+532为例,根据变形速率准则,并结合 D隧道现场监测数据,拱顶下沉速率〈0.07~0.15 mm/d时,该隨道断面二衬支护时机为25 d,距掌子面63 m。基于变形速率准则,ZK4+586、YK4+532、YK5+ 012、ZK5+034断面分别在27 d、25 d、22 d、21 d后适合施作二衬支护,故隧道二衬支护时机为21~27 d。
3.2 极限位移准则
极限位移准则:根据《锚杆喷射混凝土支护技术规范》(GB 50086-2009)规定,已产生的各项位移达到0.8~0.9倍的各项预计位移总量值(根据现场监测情况综合分析,取0.8倍的极限位移时施作二次衬挪)时,隧道适合施作二衬支护。文章根据隧道实测拱顶沉降数值,通过MATLAB软件对变形测试数据进行统计、回归分析后,采用指数函数y =Ae-B/x对拱顶沉降曲线进行拟合分析,求得位移回归方程。对D隧道ZK4+586、YK4+532、YK5+012、ZK5+ 034断面拱顶位移监测断面利用MATLAB软件进行回归分析。以ZK4+586为例,MATLAB分析拱顶沉降的极限位移公式:y=93.02e(-5.18/x),当X趋向无穷时,极限位移值为93.02 mm,其中拟合相关系数R=0.91,该断面二衬支护时机为隧道幵挖后第23 d,距掌子面58 m,具体见表2。
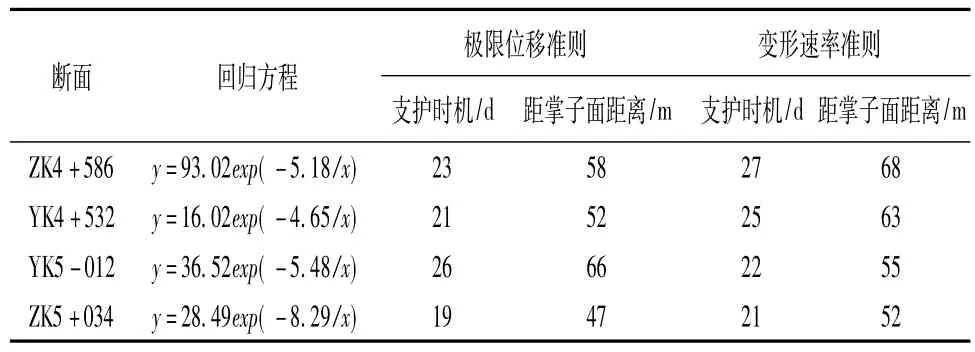
表2 隧道支护时机表
根据隧道极限位移准则,ZK4+586、YK4+532;YK5+012、ZK5+034断面分别在23 d、21 d、26 d、19 d后满足二衬支护条件,故二衬支护时机为19~26 d,距掌子面距离47~66 m。
4 结论
(1)不同的上台阶与下台阶施工错距会引起不同的隧道位移,随着上台阶与下台阶之间施工错距的增大,隧道围岩位移受影响程度变小。
(2)采用正台阶法的目的在于能在较短时间内形成支护整体,上台阶与下台阶之间的施工错距合理范围建议取值10~12 m。
(3)通过研究隧道在短时间内的不同施工错距对隧道进行了分析,事实上隧道开挖后,为了有效地利用岩土体的自稳性能,应及时形成初期支护体系。
(4)基于变形速率准则,建议二次衬砌最佳支护时机取初期支护后21~27 d;基于极限位移准则,建议二次衬砌最佳支护时机取初期支护后19~26 d。
[1] 陈秋南,包太.隧道工程[M].北京:机械工业出版社,2007:7-32.
[2] 何晖,赵敏,李宝平.土木工程测试技术[M].西安:西安工业大学出版社,2006.
U445
C
1008-3383(2015)10-0089-02
2015-01-05
周亚鸿(1978-),女,湖南望城人,工程师。
