FLAC3D中强度折减法确定掌子面极限支护压力
2020-06-05朱询泽
朱询泽, 李 斌
(武汉理工大学 交通学院,湖北 武汉 430063)
0 引 言
在隧道工程中,因地下水渗流引起的突水,突泥与塌方已经成为隧道灾害中最常见的两种灾害[1-3]。隧道开挖时,由于洞室围岩衬砌比较及时,且均为防水结构,掌子面作为唯一的透水面为地下水的渗流提供了通道,因此隧道里的涌水灾害大多发生在掌子面及其前方位置。特别是在隧道处于砂层或软弱围岩地层,发生涌水灾害时,往往会伴随着突泥和流砂等灾害,大幅度减弱掌子面的稳定性,使掌子面出现塌方。
目前对渗流作用下掌子面的稳定性已经有了大量的研究,对掌子面的研究主要有以下3种方式:①理论分析;②模型相似实验;③数值模拟方法。其中在掌子面极限支护压力的确定方法中理论分析相关的研究偏多,Leca E等[4]通过土体的三维极限平衡理论,得出了维持隧道掌子面稳定的支护压力的上限解和下限解。日本学者KANAYSU[5]对日本盾构隧道进行研究,提出了隧道开挖过程中对数螺旋线形楔形体破坏模型,并提出了该破坏模型的数值解——村山公式。Lee等[6]中以某隧道为工程背景,分析了渗流力对隧道开挖面的影响,建立了垂直条分几何模型。高健等[7]以广州地铁4号线某区间为工程背景,使用极限平衡法验证里垂直条分几何模型的正确性。吕玺琳等[8]通过对KANAYSU提出的村山破坏模型和极限分析上限法破坏模型进行对比研究,分别计算出两种方法下对应的掌子面极限支护压力数值解,并将支护压力表达式转化为三项叠加的形式。王浩然等[9]在吕玺琳研究的基础上提出了渗透作用下掌子面极限支护压力数值解的表达式。Shi等[10]在极限平衡理论的基础上,研究了矿山法隧道在富水地层施工时掌子面的破坏模型,并给出了相应的极限支护压力表达式。
但是,使用理论分析的方法确定掌子面极限支护压力有一定的局限性,首先理论分析方法计算掌子面极限支护力仅适用于单一简单地层,且极限支护压力的数值解与建立的数学模型有关,即使是同一种破坏模式,当数学模型发生变化,其数值解也会随之变化,导致计算出的掌子面支护压力也发生变化。随着计算机性能不断提高,使用数值模拟计算的方法不仅可以计算出复杂地层下的极限支护压力,且其结果较理论分析方法准确。本文将使用数值模拟软件FLAC3D中的强度折减法求解掌子面极限支护压力,并针对强度折减法计算时间较长的缺点提出一种可以快速确定掌子面极限支护压力的强度折减快速迭代方法。最后将强度折减法计算出的结果与收敛约束法和理论分析方法进行对比。
1 强度折减法确定掌子面极限支护压力
1.1 一般迭代方法
一般迭代方法是指使用强度折减法求解安全系数从而判断掌子面稳定性的分析方法。其核心理念是,通过对岩体力学性质指标(c、φ)进行折减,求出某一掌子面支护力作用下的安全系数,若此时求出的安全系数大于1,则认为掌子面稳定;若小于1,则认为掌子面失稳;当安全系数等于1时,则说明此时的掌子面支护力即为能够维持掌子面稳定性的极限支护力。当使用强度折减法确定掌子面极限支护力时,没有必要计算每一种支护力下对应的安全系数,如果使用“中值法”的思想,不断取掌子面破坏和稳定时分别对应的支护力的中间值,往往会取得事半功倍的效果。使用“中值法”求掌子面极限支护力的流程如图1所示,其过程如下:
(1)取一个较大的支护力F1使其对应的安全系数k1大于1,取一个较小的支护力F2使其对应的安全系数k2小于1。
(2)取支护力F3=(F1+F2)/2,计算出此时支护力F3所对应的安全系数k3。
(3)若F3所对应的安全系数k3大于1,则令支护力F1=F3、k1=k3;若F3所对应的安全系数k3小于1,则令支护力F2=F3、k2=k3。
(4)设ε为安全系数允许差值,若此时安全系数k1-1>ε,则重复操作(2)和(3);若k1-1≤ε,则认为此时的支护力F1即为极限支护力。
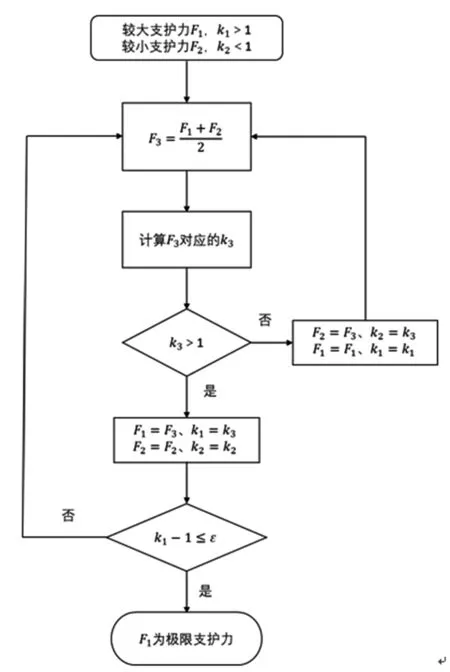
图1 一般迭代方法“中值法”求极限支护压力的流程图
1.2 快速迭代方法
使用FLAC3D 5.0中的强度折减法进行岩土剪切强度折减时,可以使用下面的命令流进行设置:
Solvefosbracketv1v2resolutionε
将FLAC3D 5.0里面进行强度折减的命令流中的两个初始折减系数v1、v2同时设置为1.0,即Solvefos bracket 1.0 1.0,此时对某一支护力下的隧道掌子面核心土进行强度折减,若此支护力下掌子面处于稳定状态即安全系数大于1,则系统会输出显示“Model is stable with reduction factor=1”,若系统输出显示为“Model is unstable with reduction factor=1”,则说明该支护力下掌子面处于失稳状态,发生坍塌。使用这种方法可以快速地判断在某一支护力下掌子面是否稳定,在FLAC3D 5.0中仅需进行一次强度折减就可以得到判断结果,不需要烦琐的循环折减。之后可以通过不断改变掌子面支护力,不断使用该方法进行稳定性判断,来寻找维持掌子面稳定的极限支护力,其流程如图2所示。
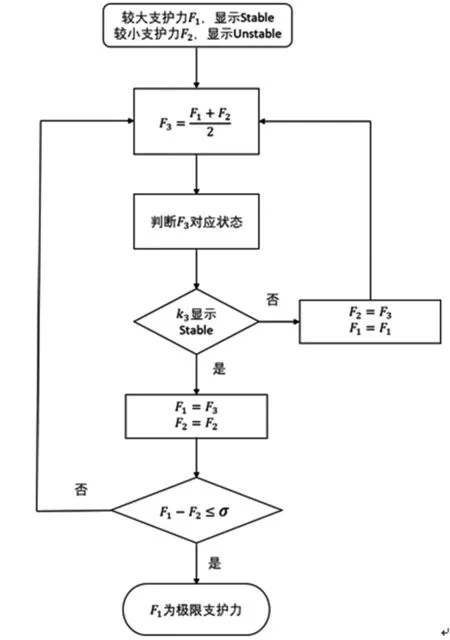
图2 快速迭代方法“中值法”求极限支护压力的流程图
强度折减快速迭代法中“中值法”选取掌子面支护压力的流程如下:
(1)取一个较大的支护压力F1使其输出显示的结果为Stable,取一个较小的支护压力F2使其输出显示的结果为Unstable。
(2)取支护力F3=F1+F22,计算出此时支护力F3所输出显示的结果。
(3)若F3所输出显示的结果为Stable,则令支护力F1=F3;若F3所输出显示的结果为Unstable,则令支护力F2=F3。
(4)设σ为支护压力允许差值,若此时支护压力F1-F3>σ,则重复操作(2)和(3),若F1-F3≤σ,则认为此时的支护力F1即为极限支护力。
快速迭代方法与一般迭代方法相比,快速方法省去了第一次“中值法”,将计算支护压力对应的安全系数这一过程进行了变换,从计算对应的安全系数变为了判断支护压力作用下掌子面是否稳定,极大地较少了计算机的计算量,较少了迭代次数,提高了工作效率。
2 掌子面极限支护压力的确定
使用软件FLAC3D进行三维数值模型。根据隧道开挖的尺寸,模型几何尺寸可以简化为:X×Y×Z=宽度×纵向×高度=66 m×60 m×42 m,隧道截面形状简化为圆形,直径为6 m。将衬砌设置为实体单元且不透水,隧道仅掌子面为自由透水面。隧道埋深为9 m,地下水位地面以下2 m渗透系数为1×10-4cm/s,模型尺寸和地下水位线分别如图3、图4所示。
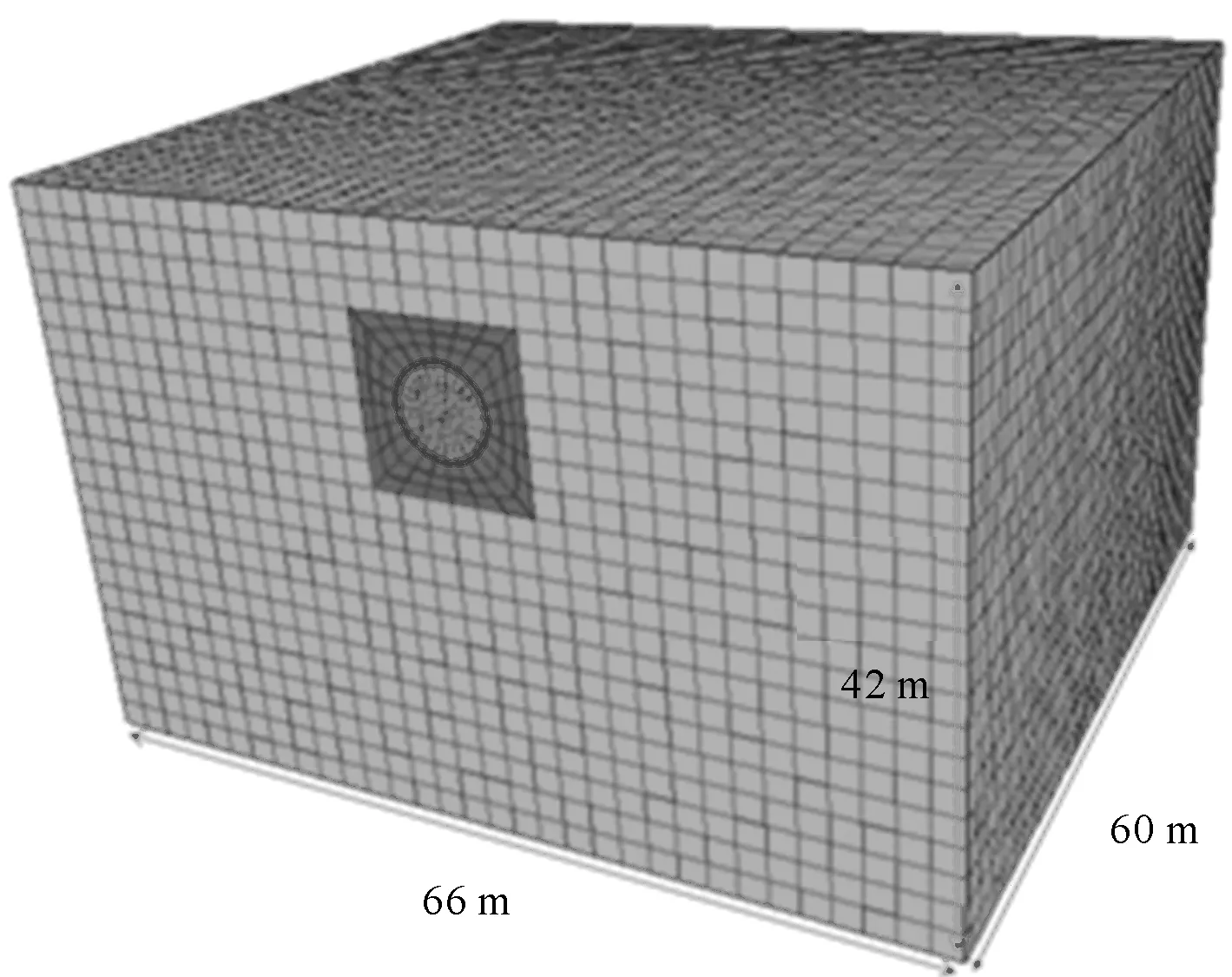
图3 模型尺寸示意图

图4 地下水位线示意图
围岩及衬砌的材料物理力学参数见表1。

表1 围岩及衬砌的材料物理力学参数
2.1 强度折减法一般迭代方法
基于“中值法”的思想使用FLAC3D中强度折减法一般方法进行安全系数求解,在本工况中将初始的较大支护力F1设置为100 kPa,较小的支护力F2设置为0,安全系数允许差值ε设置为0.01。其迭代过程见表2,需要说明的是,表中最后一项计算时间受模型网格数量和计算机处理器水平影响。
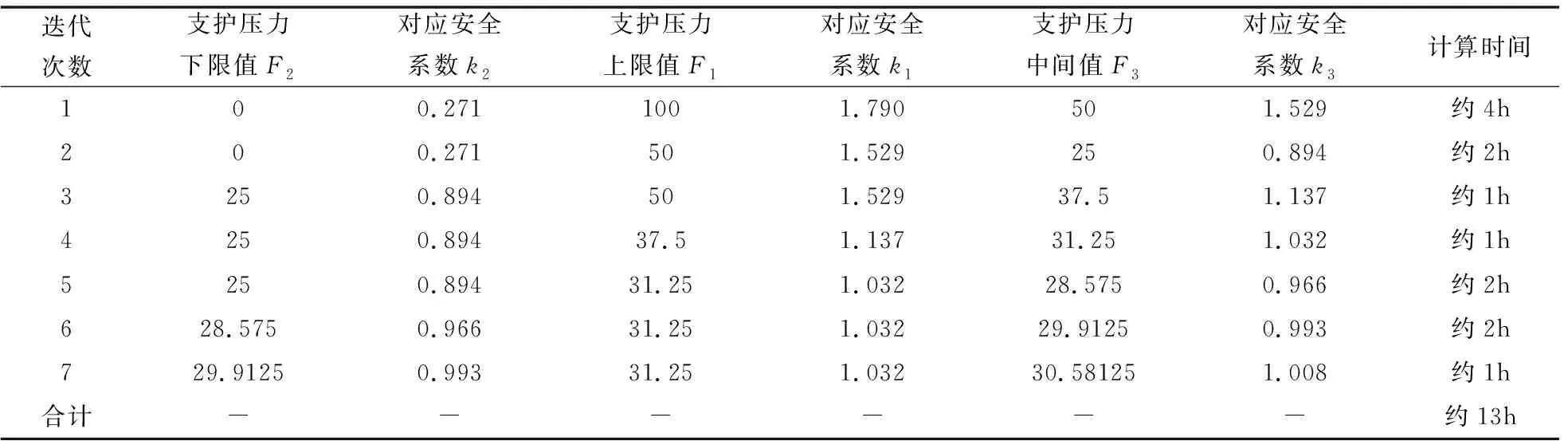
表2 一般方法求极限支护压力的迭代过程(单位:kPa)
从表2可以看出,掌子面支护压力为29.91 kPa时,对应的安全系数为0.993,小于1,此时掌子面处于失稳状态;支护压力为30.58 kPa时,对应的安全系数为1.008,与1之间的差值小于允许误差0.01,所以可以认为30.58 kPa即为该工况下掌子面的极限支护压力。与对掌子面应力应变曲线进行线性回归计算得到的极限支护压力28.86 kPa误差为5.96%。由此可见,使用强度折减法同样可以判断掌子面的稳定状态,且较收敛约束法可以更准确地计算出掌子面的极限支护力。
2.2 强度折减法快速迭代方法
基于强度折减法快速迭代方法求掌子面极限支护压力的过程,在本工况中,初始的F1和F2分别取100 kPa和0,支护压力允许差值σ为1 kPa。求解迭代过程及结果见表3。
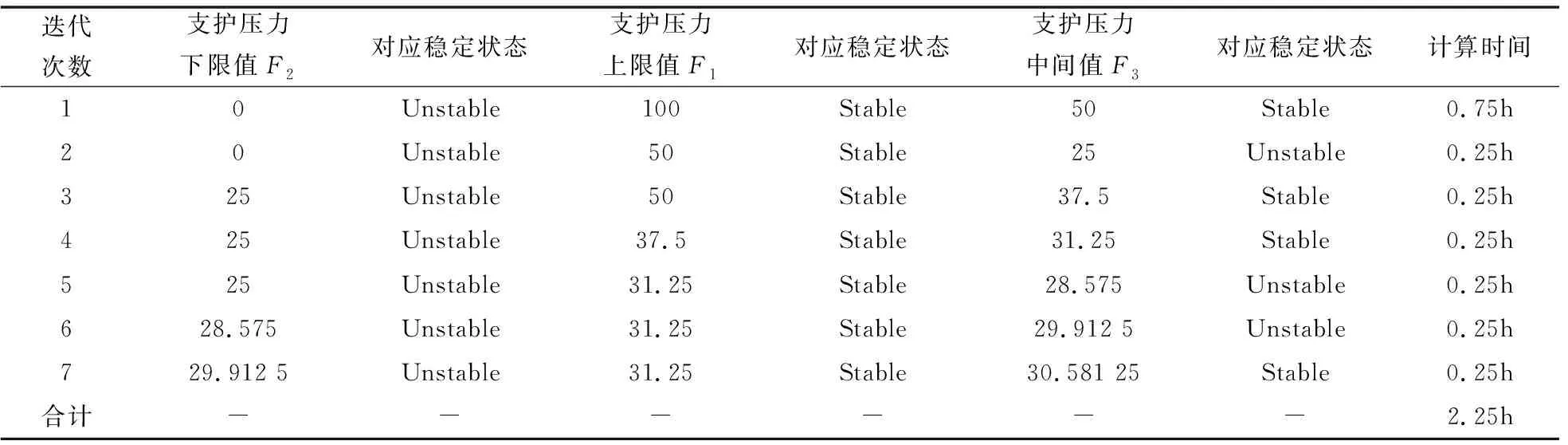
表3 快速迭代方法求极限支护压力的迭代过程(单位:kPa)
由表3可以看出,当“中值法”进行到第七次迭代计算时,此时支护压力下限值为29.912 5 kPa,中间值为30.581 25 kPa,分别对应着失稳(Unstable)和稳定(Stable)两种状态,且两者之间的差值为0.668 75 kPa,小于支护压力允许差值1 kPa,因此可以认为支护压力30.581 25 kPa即为该工况下掌子面极限支护压力。
对比两种强度折减法可以发现,在第一种方法中完成整个迭代计算所花的时间约为13 h,而在第二种方法中完成整个迭代计算所需时间仅为2.25 h,计算效率提高了将近80%。
3 对数值模拟结果进行验证
3.1 使用收敛约束法对数值模拟结果进行验证
隧道掌子面的失稳实质是掌子面上岩体的应力状态超过了其强度而发生的失稳破坏。当隧道掌子面处于极限平衡状态时,一些微小的扰动或改变,都会使打破掌子面的极限平衡状态,使掌子面发生不可逆转的变形,这种变形是掌子面极限平衡状态被破坏后的突变现象,所以掌子面挤出变形的突然增大可以作为掌子面是否稳定的判定依据。因此,基于上述理论对不同支护力作用下掌子面的挤出变形进行线性回归处理,当隧道进行开挖后,逐渐减少掌子面上的支护力,当出现支护力减少很少但是掌子面挤出位移突然增大的现象时,可认为此时掌子面处于极限支护状态,此时的支护力就为维持掌子面稳定的极限支护力。
隧道开挖过程中,围岩因为发生应力卸载,会出现朝向隧道洞室方向的变形。在模拟计算过程中,通过监控掌子面中心点的Y方向的位移,如图5所示,得出了掌子面挤出变形随掌子面支护力变化的曲线,如图6所示。
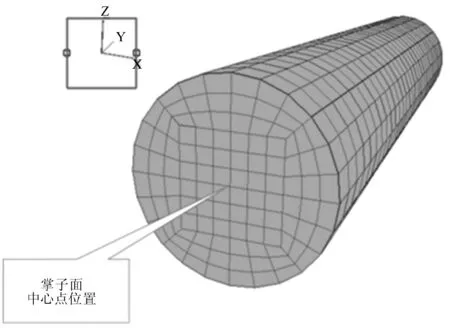
图5 掌子面监控点位置
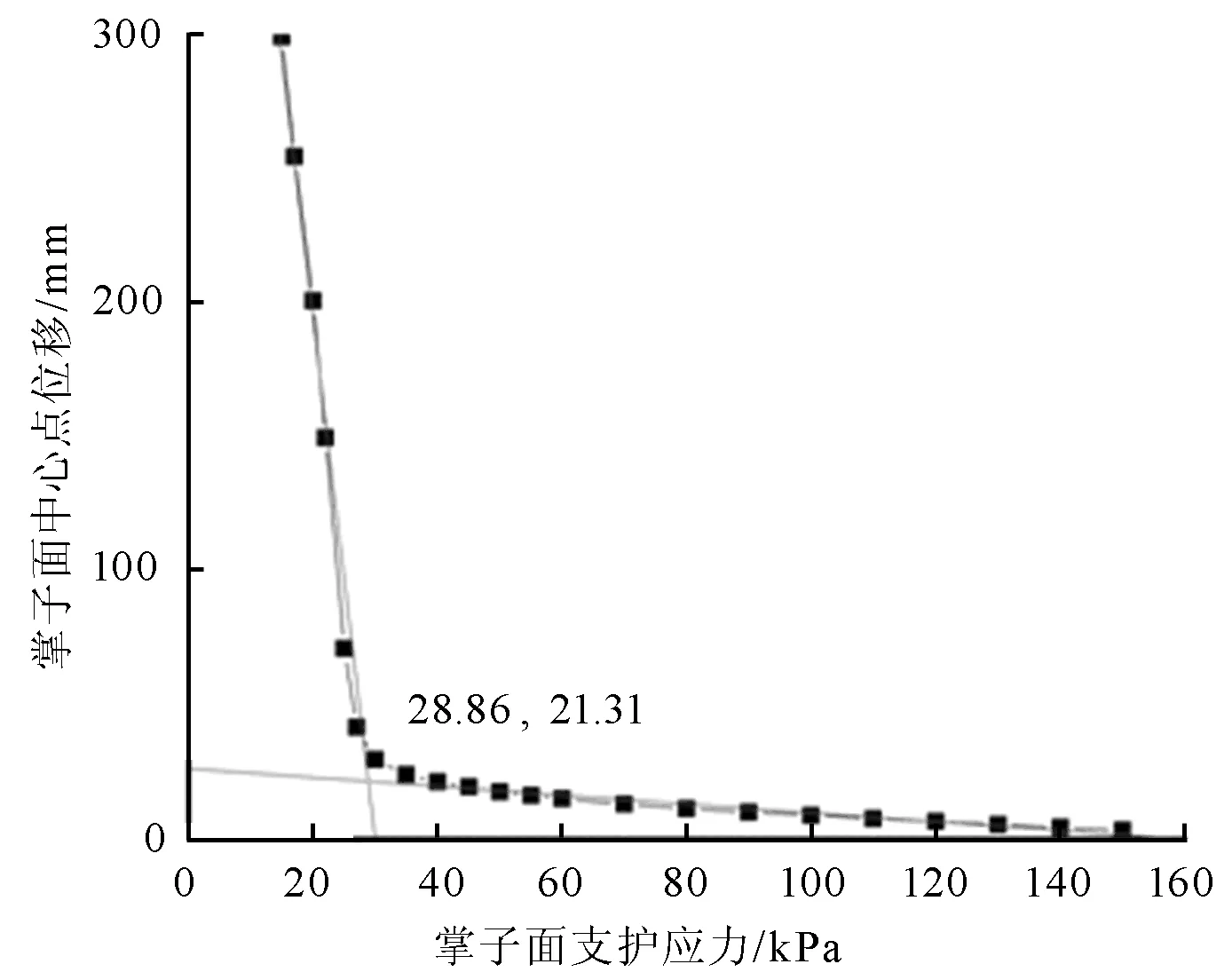
图6 掌子面挤出变形与支护压力的关系
由图6可知,掌子面的挤出位移随支护力的减小而增大,并存在突变现象,具有明显的阶段性。通过对掌子面应力应变关系进行线性回归确定图中的突变点,则突变点所对应的支护力即为极限支护力。线性回归方程组为:
{y1=630.996 42-21.125 66x
y2=26.021 19-0.163 24x
对方程组进行联立求解,得:
{x=28.86
y=21.31
横坐标即为此工况下的极限支护压力,约为28.86 kPa
3.2 使用极限分析上限法对数值模拟结果进行验证
在本节中将使用王浩然[9]提出的数值解对该工况极限支护压力进行数值计算,并将结果与强度折减法求得的掌子面极限支护压力进行比较。
在本工况中,砂层的内摩擦角为37°,隧道直径D为6 m,埋深C为9 m。可以计算出该工况下掌子面破坏模型的几何尺寸:
r0=Dsin(π/3-φ/2)cosφ·exp[(π/3+φ/2)tanφ]=0.075 6 m
h=r0cos(φ+π/12)sin(π/12+2φ)cosφ=2.85 m
lB={0(h-C≤0)
(h-C)[tan(π12+φ)+tanφ](h-C>0)
因为本工况中C=9 m,h-C≤0,所以
lB=0
根据几何尺寸,可以确定掌子面的破坏模型,如图7所示。

图7 渗流作用下掌子面破坏模型
根据公式极限分析上限法理论,可以得出掌子面上的极限支护力σt=33.026 kPa。
将4种方法求出的掌子面极限支护压力进行对比,其中,使用强度折减法求得的掌子面极限支护压力为30.58 kPa,使用收敛约束法求得的掌子面极限支护压力为28.86 kPa,使用极限分析上限法求解出的掌子面极限支护压力为33.03 kPa,3种方法求得极限支护压力误差在5 kPa以内,其中虽然极限分析上限法求解出的支护压力与收敛约束法求出的极限支护压力误差约为12.6%,但是考虑到两者之间的极限支护压力差值仅为4.17 kPa,可以认为这种误差是能够接受的。
4 总 结
本文介绍了通过数值模拟软件FLAC3D使用强度折减法确定掌子面极限支护压力的过程,并针对强度折减法计算时间过长这一缺点,提出了一种基于强度折减法快速计算掌子面极限支护压力的新方法,并结合案例,使用收敛约束法和理论分析方法中的极限分析上限法对强度折减法计算结果进行了验证。得出结论:
(1)使用强度折减法同样可以计算出掌子面极限支护压力,且相比较于收敛约束法和理论分析方法,强度折减法的计算结果更加准确。
(2)当不需要计算掌子面在各种支护压力下具体的安全系数时,可以通过对FLAC3D中的强度折减法进行设置,仅判断掌子面在各种支护压力下是否稳定,之后再使用“中值法”流程找出极限支护压力,这种方法相比传统的强度折减法,计算时间大幅缩减,计算效率大幅提高。
