曲面拟合法和梯度法相结合的图像亚像素配准算法*

刘红亮，陈维义，许中胜(.海军工程大学兵器工程系，湖北武汉430033；.海军驻中南地区光电系统军事代表室，湖北武汉430073)

曲面拟合法和梯度法相结合的图像亚像素配准算法*

刘红亮1，陈维义1，许中胜2
(1.海军工程大学兵器工程系，湖北武汉430033；2.海军驻中南地区光电系统军事代表室，湖北武汉430073)

针对传统亚像素配准算法存在精度不高、计算复杂的问题，提出了一种曲面拟合法和梯度法相结合的图像亚像素配准算法。采用9点相关系数曲面拟合法对图像进行粗配准，求得一个相对粗略的亚像素配准位置；在两幅图像中选取相同尺寸的子区图像，在粗略的亚像素配准位置基础上，采用梯度法最终获得精确的亚像素配准位置。不同平移关系下的样本图像亚像素配准对比实验结果表明，该算法实现了曲面拟合法和梯度法的优势互补，有效提高了图像配准的精度，最大配准绝对误差由0.17像素降低为0.02像素。

图像配准；亚像素；曲面拟合法；梯度法；泰勒展开

近年来，基于图像配准的测量系统在很多领域得到广泛应用，为了提高测量精度，除了采用更高分辨率和更大放大倍数的光学成像系统，还可以在现有光学成像系统的基础上对图像进行亚像素位移测量［1］。实践证明，在许多的情况下，整像素的位移测量很难满足实际的需要，亚像素配准技术是提高测量精度的一种有效的方法［2］。常用的亚像素配准算法主要有灰度插值法、曲面拟合法和梯度法等［3］。其中，灰度插值法是采用插值技术重构原始图像和待配准图像的亚像素灰度场，然后在插值后的新图像上进行相关搜索，最终获得亚像素级的配准精度。如果将插值步长改为0.1像素，就能得到0.1像素级别的配准精度。虽然这种算法的配准精度相对较高，但是配准结果受图像插值函数性能的影响很大，而且计算量很大，还容易受图像噪声的影响，应用效果并不理想，因而在实际中使用较少［4］。曲面拟合法和梯度法下文会详细介绍，此处不再赘述。

文献［5］和文献［6］分别对异源图像和SAR图像的配准问题进行了分析，但研究的侧重点在于图像像素级配准时的特征提取、相似性测度和搜索策略等方面，因此图像配准的精度有限。文献［7］针对行星中心定位问题提出了改进的亚像素边缘检测算法，并采用修正项以进一步提高亚像素边缘检测精度，研究思路对本文有一定启示。文献［8］提出了一种结合空域灰度投影和频域相位相关的亚像素图像配准方法，即在空域采用灰度投影算法对运动图像进行粗配准，在频域采用扩展的相位相关算法对图像进行精确配准；但是，这种方法的配准误差会随着两幅图像位移量的增大而越来越大。

本文算法具有从粗略到精确的特点，实现了曲面拟合法和梯度法这两种亚像素配准算法的优势互补，有效提高了图像配准的精度。

1 传统的亚像素配准算法

1.1 相关系数曲面拟合亚像素配准算法

曲面拟合法是在获得原始图像和待配准图像的整像素配准位置的基础上，利用整像素配准位置周围各点的相关系数矩阵进行二次曲面、高斯曲面或拉格朗日曲面拟合，然后通过求拟合函数的极值来获得相应的亚像素配准位置的方法。高斯曲面拟合或拉格朗日曲面拟合不仅需要较大的拟合窗口，而且可能产生较大的误差，因此实际中多采用二元二次多项式来拟合相关系数曲面［9-10］，相应的曲面拟合函数为:

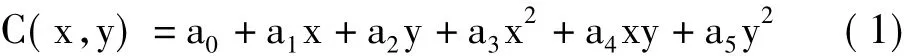
假定数字图像相关法搜索到的整像素配准位置为(x0，y0)，该点的相关系数用C(0，0)表示，其周围8点的相关系数依据相对位置关系，依次设为C(-1，-1)…C(1，1)，如图1所示。设

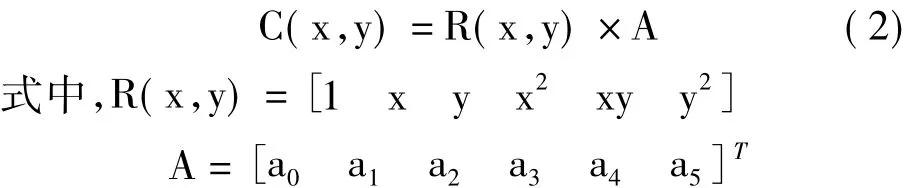
采用这9点相关系数拟合式(1)的二元二次曲面，将x=-1∶1，y=-1∶1分别带入R(x，y)和C(x，y)，用最小二乘法就可以得到该二元二次多项式的系数a0，a1，a2，a3，a4和a5。该曲面拟合函数的极值位置应满足方程组

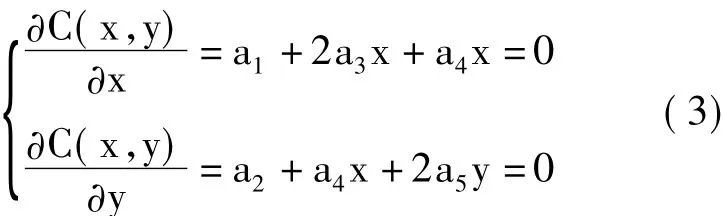
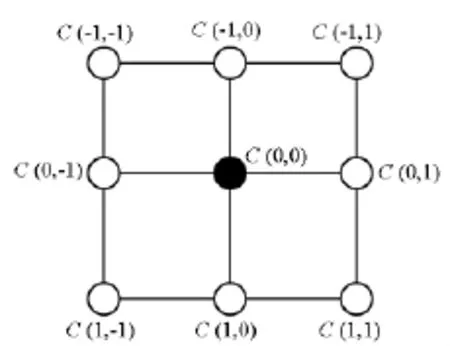
图1 相关系数曲面拟合法示意图Fig.1 Diagram of curved surface fittingmethod based on correlation coefficients

可以求出拟合曲面的极值点的位置为［11］

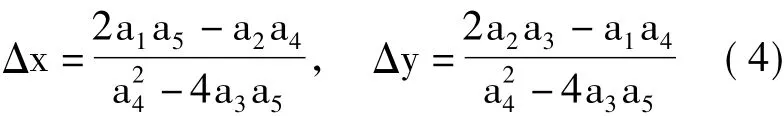
结合事先已求得的整像素配准位置(x0，y0)，两幅图像最终的亚像素配准位置为

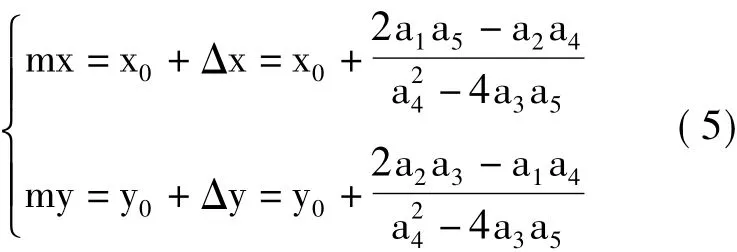
基于相关系数曲面拟合法的亚像素配准算法仅仅依靠整像素配准位置及其周围8点的相关系数即可迅速确定亚像素配准位置，因此具有计算效率高、抗噪声能力较强等优点，在实际中得到广泛使用。但是由于曲面拟合函数通常无法完全描述相关系数的分布特性，因而曲面拟合法获得的拟合结果就很难达到更高的精度要求，这又使它在高精度亚像素配准方面的应用受到一定的限制。

1.2 基于梯度的亚像素配准算法

基于梯度的亚像素位移算法最初是从光流计算中引入并应用到图像配准定位中的。该算法的基本思想如下:令f(x，y)和g(x*，y*)分别表示原始图像和待配准图像相应子区图像的灰度值。当子区图像足够小且作微小位移时，则该子区可以近似看作是刚体运动［12］。即

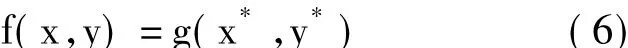
式中，x*=x+x0+Δx，y*=y+y0+Δy。x0，y0和Δx，Δy分别代表两幅图像相应子区图像在x，y方向的整像素位移和亚像素位移。梯度法就是利用原始图像和待配准图像相应子区图像的灰度值和梯度值建立目标函数，再对目标函数求极值来获得相应的亚像素配准位置的方法。

将g(x+x0+Δx，y+y0+Δy)在(x+x0，y+ y0)处分别进行一阶和二阶泰勒级数展开并舍去高阶小量，则有

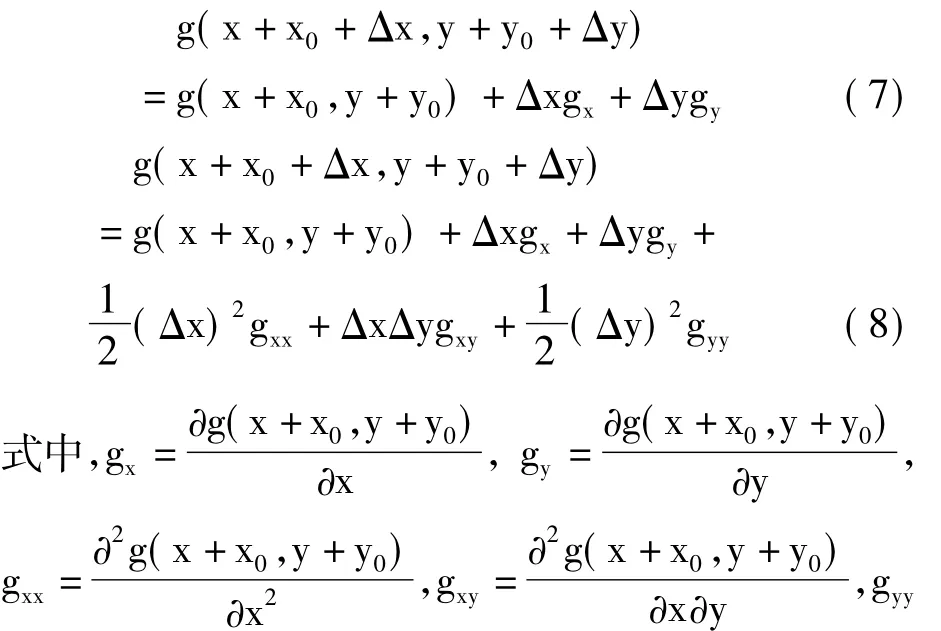
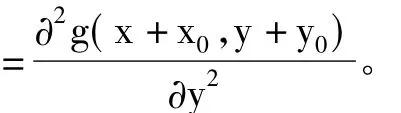
显然，二阶泰勒级数展开的算法复杂度要更高，计算量要更大。因此通常进行一阶泰勒级数展开［13］。式(7)、式(8)中梯度gx和gy的计算采用计算结果精确、性能稳定的Barron算子［14］

结合事先已知的整像素位移(x0，y0)，即可求得两幅图像的最终的亚像素配准位置。

基于梯度的亚像素配准算法有明确的数学原理和适中的算法复杂度，易于实现，配准精度高。但是该算法也有着明显的不足之处。在对g(x+ x0+Δx，y+y0+Δy)在点(x+x0，y+y0)处进行一阶泰勒级数展开时，由于忽略了高阶小量，引入的误差必将随着Δx，Δy的增大而增大，而使用计算精度更高的二阶泰勒级数展开又会导致计算量的增加［15］。也就是说，只有在亚像素位移Δx，Δy都较小(通常小于0.15像素)的时候，g(x+x0+ Δx，y+y0+Δy)的一阶泰勒展开误差才会较小，才能确保最终获得更为精确的亚像素配准位置。

2 曲面拟合法和梯度法相结合的亚像素配准算法

曲面拟合亚像素配准算法的计算效率高，应用广泛，但是很难获得高精度的亚像素配准结果；基于梯度的亚像素配准算法易于实现，求解效率也相对较高，但是亚像素配准精度受到泰勒级数展开误差(主要是展开阶数和展开位置)影响很大；由于忽略了高阶小量，只有在较为精确的展开位置上进行一阶泰勒展开时才能获得理想的亚像素配准精度。曲面拟合法和梯度法相结合的亚像素配准算法的基本思想就是充分发挥这两种算法的优点，首先采用曲面拟合法求得一个相对粗略的亚像素配准位置，再以此配准位置作为梯度法在一阶泰勒展开时的展开位置，从而减小泰勒展开的误差，最终获得一个精度大大提高的亚像素配准位置。

假定原始图像和待配准图像真实的亚像素配准位置为(x0+h，y0+k)，采用曲面拟合法求得的亚像素配准位置为(x0+Δx，y0+Δy)，显然，Δx和Δy是对h和k的良好估计。令s=x+x0+Δx，t =y+y0+Δy，对g(x+x0+h，y+y0+k)进行一阶泰勒展开并舍去高阶小量，有

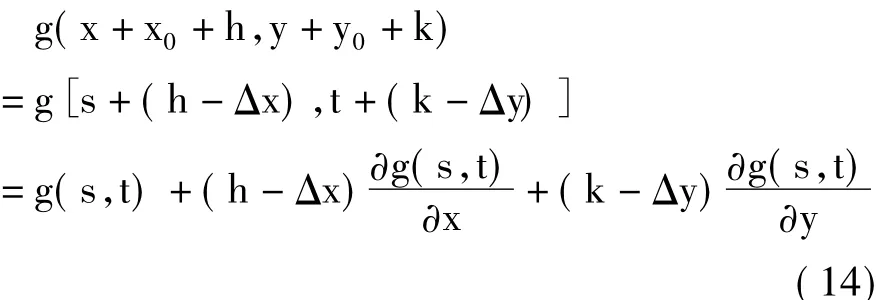
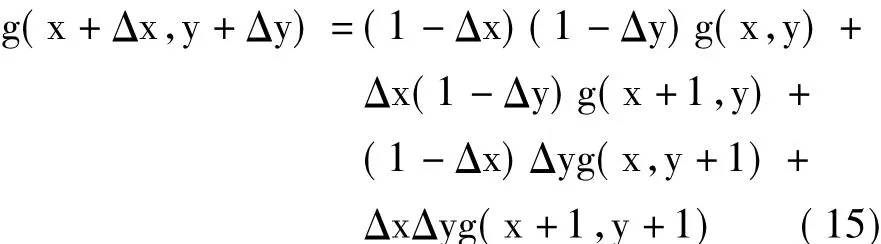
由于Δx和Δy是对h和k的良好估计，h-Δx和k-Δy相比于Δx和Δy就会小很多，相对于式(7)，式(14)就会在很大程度上减小一阶泰勒级数展开时的误差。令

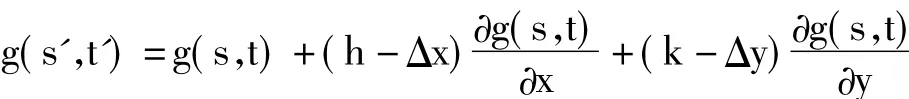
则新算法的目标函数为

结合事先已求得的(x0，y0)和Δx，Δy，即可求得两幅图像最终的亚像素配准位置(x0+h，y0+ k)。可见，曲面拟合法和梯度法相结合的亚像素配准算法是在整像素配准位置上采用曲面拟合法求得粗略的亚像素配准位置，再在该粗略的亚像素配准位置上采用梯度法求得精确的亚像素配准位置，新算法流程如图2所示。

图2 新亚像素配准算法流程Fig.2 Flow chart of the new sub-pixel registration algorithm

3 仿真实验与分析

3.1 测试图像的生成

原始图像来自车载成像设备获取的地面可见光图像，图像分辨率为1280×1920像素，位移图像通过对原始图像平移得到。通过对存在整像素平移关系的两幅图像做10倍下采样的方法，便可得到存在亚像素平移关系的原始图像和待配准图像［16］。

为方便计算，本文只对原始图像进行水平方向的平移操作。依次对原始图像进行步长为13像素的水平平移操作，一共生成10帧位移图像。相对于原始图像，第n帧位移图像的水平位移dx =1+13×(n-1)像素；再对原始图像和10帧平移图像做10倍下采样，便得到大小均为128× 192像素，平移关系依次为向右平移0.1，1.4，2.7，4.0，5.3，6.6，7.9，9.2，10.5和11.8像素的10帧位移图像。各帧位移图像的亚像素位移量如图3所示。

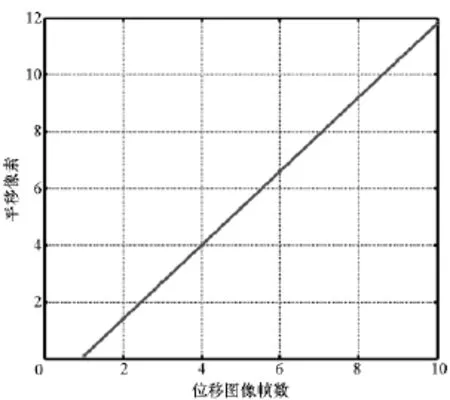
图3 图像间亚像素位移关系曲线Fig.3 Curve diagram of sub-pixel displacement

3.2 实验结果分析

采用数字图像相关法，可以轻易求得平移关系依次为0.1，1.4，2.7，4.0，5.3，6.6，7.9，9.2，10.5和11.8像素的10帧位移图像与原始图像的整像素配准位置依次为0，1，3，4，5，7，8，9，11和12像素。在事先获得整像素配准位置的前提下，我们分别采用曲面拟合法和梯度法对原始图像和10帧位移图像进行亚像素配准，配准结果见表1。显然，在使用梯度法求解亚像素配准位置时，位移图像正是以整像素配准位置作为其一阶泰勒级数的展开位置。

由表1可知，曲面拟合法和梯度法均可获得相对准确的亚像素配准位置。图4显示的是这两种算法的亚像素配准位置与真实平移关系的绝对误差。可见，当真实平移关系为0.1，4.0，7.9，9.2和11.8像素时，梯度法中一阶泰勒级数的展开位置(依次为0，4，8，9和12像素)与真实平移关系的差的绝对值较小(0～0.2像素)，因此，相比于曲面拟合法，梯度法的配准结果与真实平移关系的绝对误差就较小；当真实平移关系为1.4，2.7，5.3，6.6和10.5像素时，梯度法中一阶泰勒级数的展开位置(依次为1，3，5，7和11像素)与真实平移关系的差的绝对值较大(0.3～0.5像素)，因此，梯度法的配准结果与真实平移关系的绝对误差就相对较大，绝对误差的最大值为0.17像素。实验结果很好地验证了1.2节中的结论:只有在一阶泰勒级数的展开位置与真实平移关系的差的绝对值较小的情况下，位移图像的一阶泰勒展开误差才会较小，采用梯度法才能获得更加精确的亚像素配准位置。

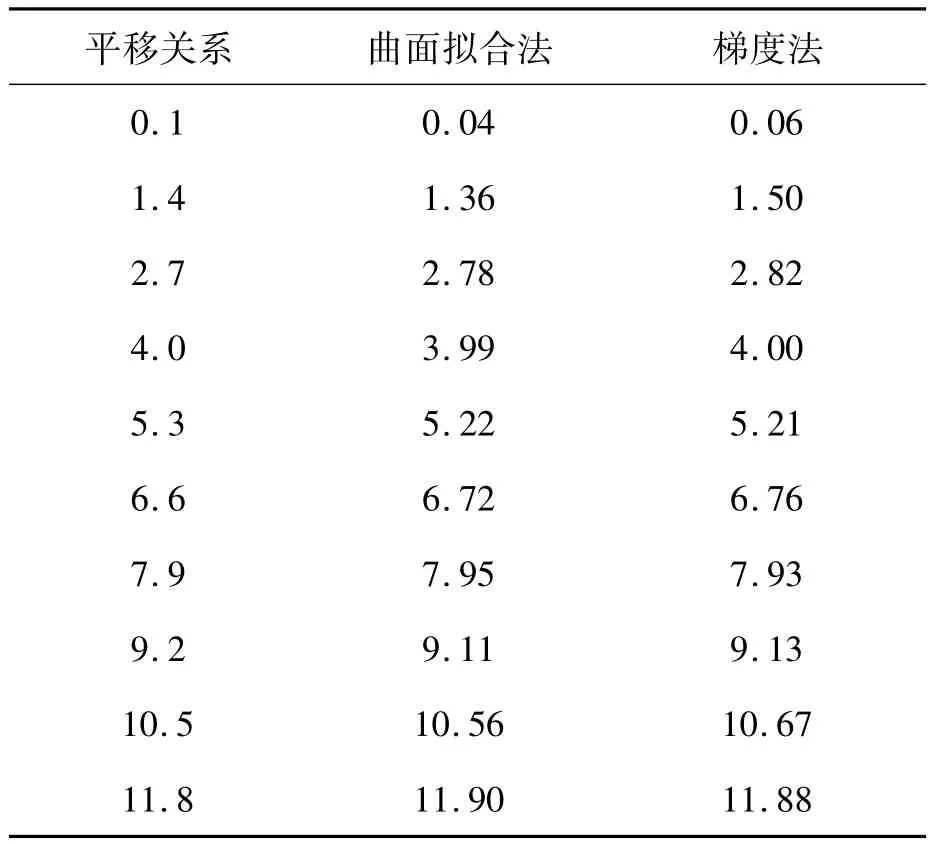
表1 传统亚像素配准算法结果Tab.1 Registration results of traditional algorithms

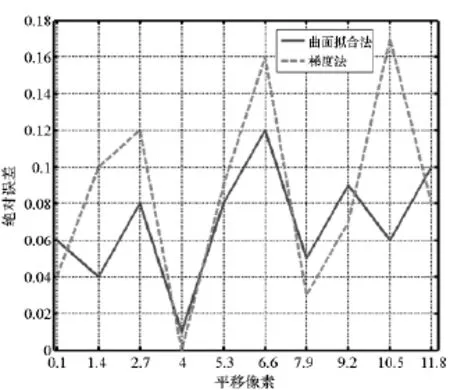
图4 传统亚像素配准算法的绝对误差Fig.4 Absolute error of traditional registration algorithms

相比于10帧位移图像与原始图像的整像素配准位置，相关系数曲面拟合法求得的亚像素配准位置与真实平移关系的差的绝对值(0.01～0.12像素)则要小很多，而曲面拟合法和梯度法相结合的亚像素配准算法正是以相关系数曲面拟合法的亚像素配准位置作为梯度法的一阶泰勒级数的展开位置，因此，采用曲面拟合法和梯度法相结合的亚像素配准算法必将获得更为精确的亚像素配准位置，新算法配准结果见表2。

曲面拟合法和梯度法相结合的亚像素配准算法尽管算法复杂度稍有增加，但是对比表2和图4不难发现，新算法具有更高的亚像素配准精度，配准结果与真实平移关系的绝对误差的最大值由传统亚像素配准算法的0.17像素降低为0.02像素，配准精度几乎提高了一个数量级。

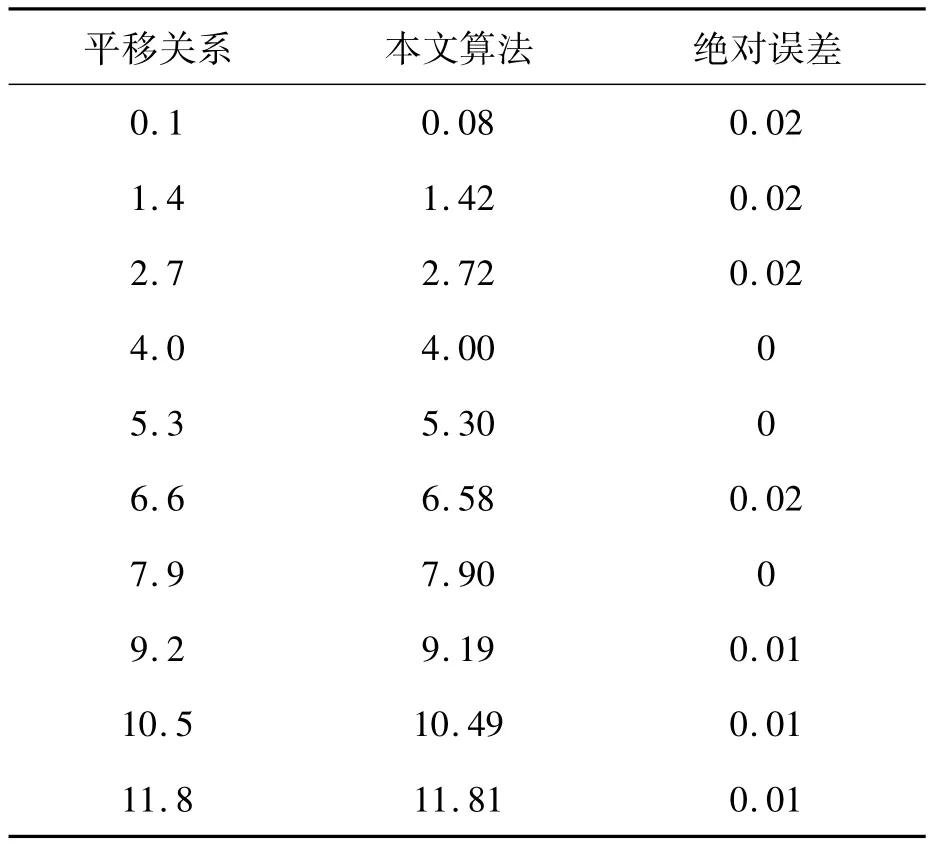
表2 本文亚像素配准算法结果Tab.2 Registration results of the proposed algorithm

4 结论

本文在分析传统图像亚像素配准算法局限性的基础上，提出了一种曲面拟合法和梯度法相结合的亚像素配准算法。新算法在曲面拟合法过程中采用9点相关系数拟合二元二次曲面，同时在梯度法过程中采用Barron梯度算子和双线性插值法，从而折中考虑了算法在精确性和实时性两个方面的性能；为减小梯度法在一阶泰勒级数展开时的误差，新算法将曲面拟合法求得的粗略的亚像素配准位置作为梯度法的泰勒级数展开位置，确保最终获得更为精确的亚像素配准位置；最后以地面可见光图像为测量对象，以曲面拟合法和梯度法为对比实验，对新的图像亚像素配准算法进行了实验验证。实验结果表明:曲面拟合法和梯度法相结合的亚像素配准算法尽管算法复杂度稍有增加，但是新算法实现了曲面拟合法和梯度法的这两种算法的优势互补，大大提高了图像配准的精度，最大配准绝对误差不足传统亚像素配准算法的八分之一；新算法在实时性和有效性方面达到了很好的平衡，具有很高的应用价值。

参考文献(References)

［1］Ma S P，Jin G C.New correlation coefficient designed for digital speckle correlation method(DSCM)［J］.Proceedings of SPIE-the International Society for Optical Engineering，2003，5058:25-33.

［2］Schneider SC，Rupitsch SJ，Zagar BG.Signal processing for laser speckle strain-measurement techniques［J］.IEEE Transactions on Instrumentation and Measurement，2007，56(6):2681-2687.

［3］张爱华，娄小平，吕乃光.数字图像相关中亚像素算法的比较［J］.北京信息科技大学学报(自然科学版)，2013，28(3):53-56.ZHANG Aihua，LOU Xiaoping，LYU Naiguang.Comparison of sub-pixel algorithms based on digital image correlation［J］.Journal of Beijing Information Science＆Technology University，2013，28(3):53-56.(in Chinese)

［4］Ma L，Zhou SS，He Z F，et al.Image sub-pixel recognition method for optical precise adjustment［C］//Proceedings of IEEE Conference on Measurement，Information and Control，2012:1439-1444.

［5］李想，雷志辉，朱宪伟，等.基于分割相似度的异源图像匹配算法［J］.国防科技大学学报，2013，35(6): 116-119.LI Xiang，LEI Zhihui，ZHU Xianwei，et al.Multi-sensor imagematching based on segmentation similarity［J］.Journal of National University of Defense Technology，2013，35(6): 116-119.(in Chinese)

［6］陈天泽，李燕.基于联合相似测度的SAR图像边缘点特征配准方法［J］.国防科技大学学报，2013，35(4): 67-73.CHEN Tianze，LIYan.The edge point registration method of SAR images based on the joint similarity［J］.Journal of National University of Defense Technology，2013，35(4): 67-73.(in Chinese)

［7］陈阔，冯华君，徐之海，等.亚像素精度的行星中心定位算法［J］.光学精密工程，2013，21(7):1881-1890.CHEN Kuo，FENG Huajun，XU Zhihai，et al.Sub-pixel location algorithm for planetary center measurement［J］.Optics and Precision Engineering，2013，21(7):1881-1890.(in Chinese)

［8］孙辉，李志强，孙丽娜，等.一种空域和频域相结合的运动图像亚像素配准技术［J］.中国光学，2011，04(2): 154-160.SUN Hui，LI Zhiqiang，SUN Lina，et al.Sub-pixel registration of special and frequency domains for video sequences［J］.Chinese Journal of Optics，2011，04(2): 154-160.(in Chinese)

［9］Shortis M R，Clarke TA，Short T.Comparison of some techniques for the sub-pixel location of discrete target images［C］// Proceedings of SPIE，1994，2350:239-250.

［10］潘兵，谢惠民，续伯钦，等.数字图像相关中的亚像素位移定位算法进展［J］.力学进展，2005，35(3):345-352.PAN Bing，XIE Huimin，XU Boqin，et al.Development of sub-pixel displacements registration algorithms in digital image correlation［J］.Advances in Mechanics，2005，35(3): 345-352.(in Chinese)

［11］Wei S D，Lai S H.Fast template matching based on normalized cross correlation with adaptive multilevel winner update［J］.IEEE Transactions on Image Processing，2008，17(11):2227-2235.

［12］Viola P，Jones M.Rapid object detection using a boosted cascade of simple features［C］.//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition，2001:511-518.

［13］Foroosh H，Zerubia J B，Berthod M.Extension of phase correlation to sub-pixel registration［J］.IEEE Transactions on Image Processing，2002，11(3):188-200.

［14］刘承兰，高勋章，贺峰，等.一种基于相位校正的InISAR图像配准新方法［J］.国防科技大学学报，2011，33(5): 116-122.LIU Chenglan，GAO Xunzhang，HE Feng，et al.A novel method for image registration in InISAR imaging based on phase correction［J］.Journal of National University of Defense Technology，2011，33(5):116-122.(in Chinese)

［15］Zhou P，Goodson K E.Sub-pixel displacement and deformation gradientmeasurement using digital image/speckle correlation［J］.Optical Metrology，2001，40(8): 1613-1620.

［16］李禄，范大昭.利用改进的相位相关算法实现影像亚像素匹配［J］.测绘科学技术学报，2013，30(6):597-601.LILu，FAN Dazhao.Application of sub-pixelmatching based on enhanced phase correlation algorithm［J］.Journal of Geomatics Science and Technology，2013，30(6):597-601.(in Chinese)

An image sub-pixel registration algorithm based on combination of curved surface fitting method and gradientmethod

LIU Hongliang1，CHENWeiyi1，XU Zhongsheng2
(1.Department ofWeaponry Engineering，Naval University of Engineering，Wuhan 430033，China；2.Navy Representative Office of Electro-Optics Systems in Zhongnan Area，Wuhan 430073，China)

In order to overcome the disadvantages of the low registration accuracy and the computational complexity of traditional algorithms，a new sub-pixel registration algorithm based on combination of curved surface fitting method and gradientmethod was proposed.Firstly，curved surface fittingmethod based on 9 correlation coefficientswasused to achieve the image rough registration.Secondly，subimageswere extracted from the reference images according to a predefined selection method.At last，gradientmethod based on the rough registration was proposed to achieve the accurate sub-pixel registration.Test results among experimental imageswith different translational relations show that the new algorithm has the advantages of both curved surface fitting method and gradient method，and greatly improves the accuracy of image sub-pixel registration.The maximum absolute error of registration accuracy is reduced from 0.17 pixel to 0.02 pixel.

image registration；sub-pixel；curved surface fittingmethod；gradientmethod；Taylor expansion

TP751.1

A

1001-2486(2015)05-180-06

10.11887/j.cn.201505028

http://journal.nudt.edu.cn

2014-10-12

国家部委资助项目(9140A09031213JB11123)

刘红亮(1986—)，男，河南邓州人，博士研究生，E-mail:lhl_hjgc@163.com；陈维义(通信作者)，男，教授，博士，博士生导师，E-mail:Fredchen118@sohu.com