圆周SAR与线性SAR成像特性分析与对比*

贾高伟，常文革(国防科技大学电子科学与工程学院，湖南长沙410073)

圆周SAR与线性SAR成像特性分析与对比*

贾高伟，常文革
(国防科技大学电子科学与工程学院，湖南长沙410073)

圆周合成孔径雷达因其独特优势已经成为雷达领域的研究热点。分析圆周合成孔径雷达与线性合成孔径雷达在成像区域大小、点散布函数特性、回波频谱特点、三维成像能力等方面的差异，凸显了圆周合成孔径雷达的成像特点。发现单航过圆周合成孔径雷达频域成像处理的难点在于其回波频谱的空变性。为提高频域成像处理的效率，分析了平面圆周合成孔径雷达与多航过圆周合成孔径雷达成像模式，并指出这两种模式易于在频域开展一致化处理。仿真试验证明了分析内容的正确性。

圆周合成孔径雷达；线性合成孔径雷达；回波频谱；点散布函数；三维成像

通过对感兴趣区域进行全方位长时间的观测，圆周合成孔径雷达(Circular Synthetic Aperture Radar，CSAR)具有二维超高分辨力、高信噪比以及能三维成像等突出优势［1-6］，已成为SAR领域的研究热点。目前，瑞典防务研究院［7］、法国宇航局［8］、德国宇航中心［9-11］及中国科学院电子所［12-13］已开展了圆周SAR的机载试验，初步验证了其独特优势。

就成像技术而言，目前圆周SAR的成像算法并不成熟。在机载试验中广泛采用的成像算法为后向投影算法(Back-Projection，BP)及其改进型快速BP算法［9］。BP算法的优点是处理过程简单，且对雷达轨迹的依赖性很低。近年来快速后向投影算法［9］(Fast Factorized Back Projection，FFBP)的出现较大地减小了BP算法的计算量并有力促进了其在实际系统中的应用。总的来讲，尽管人们可以利用BP算法获得圆周SAR相参积累结果，但却从未停止对具有更好效率的频域成像算法的探索。贾高伟等基于频域信号分析对圆周SAR的成像特性进行研究，这对开展圆周SAR的频域成像处理具有指导性作用。

线性轨迹SAR，包括条带SAR、聚束SAR、滑动聚束SAR等，在成像技术方面已日臻成熟［14］，相应的频域成像算法是人们最为常见和熟悉的SAR数据处理方式。贾高伟等通过对比圆周SAR与线性SAR的成像特性差异凸显了圆周SAR的成像特点。分析表明，单航过圆周SAR频域成像处理的难点体现在其回波频谱的空变性，这不利于在频域进行一致化处理以提高成像效率。为提高圆周SAR频域成像处理效率，贾高伟等从信号频谱分析的角度指出多航过圆周SAR成像模型易于在频域开展高效率成像处理，且具有三维精确成像的能力。

1 圆周SAR成像模型简介

圆周SAR的成像几何模型如图1所示，图1中雷达沿半径为R的圆周运动，方位向观测角为θ，雷达天线相位中心(Array Phase Center，APC)的三维坐标为(xr，yr，H)，其极坐标表示为(R cosθ，R sinθ，H)。

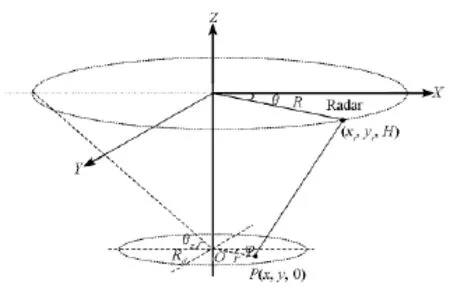
图1 圆周SAR成像几何Fig.1 Geometry of CSAR

在雷达运动过程中，雷达波束始终指向半径为Ra的成像区域。设定成像区域为水平地面，其中某一点目标P的坐标为(x，y，0)，其极坐标表示为(r cosφ，r sinφ，0)，O为坐标原点。θz表示场景中心点对应的雷达入射角。直观地，可以得到雷达APC同目标P之间的瞬时斜距为:

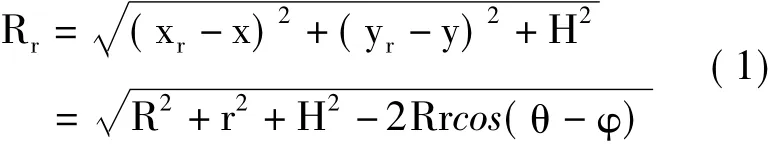
设雷达发射信号为线性调频信号(Linear Frequency Modulation，LFM):

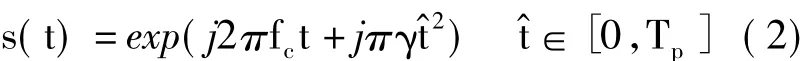
其中，fc和γ分别为LFM信号的载频和调频率，LFM信号的持续时间是Tp，t为时间变量，^t为快时间变量。针对点目标P，其雷达回波经快时间域匹配滤波后可以表示为:

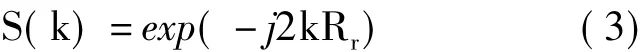
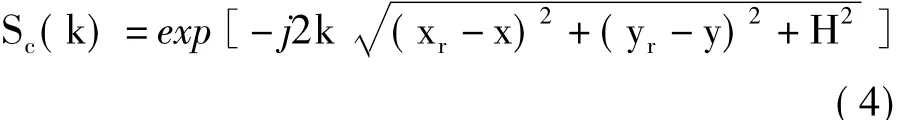
对于线性SAR(以条带SAR为例)，雷达APC同目标P之间的瞬时斜距可以表示为:

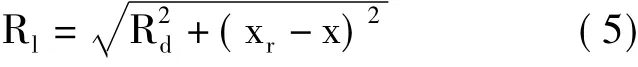
其中，Rd表示条带SAR雷达APC同目标之间的零多普勒斜距。类似于式(4)，可以得到条带SAR模式下目标P对应的雷达回波为:

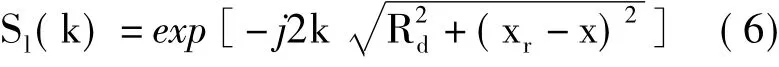
2 圆周SAR与线性SAR的差异

2.1 成像区域大小及数据处理平面的选择

以条带SAR为例，当雷达运行轨迹确定，其距离向的测绘带宽由雷达波束入射角以及波束俯仰宽度决定；方位向测绘带宽则没有限制。鉴于线性SAR系统可以涵盖单/双站SAR，为表述准确，文中线性SAR专指线性单站正侧视条带SAR。依据图1，圆周SAR工作模式下，当雷达运行轨迹确定，雷达有效观测区域的大小由“波足”决定:观测区域半径同载机飞行半径之间满足Ra≈R sin(Θw/2)，Θw为天线方位向波束宽度。对比发现，在雷达运行高度及入射角确定的情况下，圆周SAR对应的观测场景小于条带SAR工作模式的。

此外，对于线性SAR，人们通常选用斜距平面进行成像处理，且最终的雷达成像结果亦可以展现在斜距平面上。针对圆周SAR，其回波录取面不再是一个平面。为此，圆周SAR的成像处理结果一般呈现在水平平面，即为正射雷达图像。

2.2 频谱支撑域及点散布函数

由式(6)，可以获得线性SAR回波对应的相位历程为:

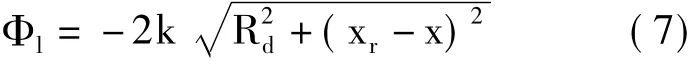
定义kR=2k为视线方向(Line Of Sight，LOS)的波数，ka表示线性SAR沿航向的波数，即为:

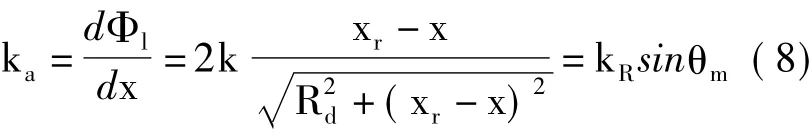
其中θm为线性SAR瞬时方位角。式(8)表明了ka的取值同目标方位向位置无关，这一特性被称为“方位不变性”。该特性有利于在多普勒频域开展一致化处理以提高成像效率。此外，式(8)表明线性SAR回波频谱支撑域的形状(kR，ka)= (2k，2k sinθm)为梯形，且与目标位置无关。

图2展现了大家熟知的条带SAR回波频谱支撑域，结合线性SAR知识［14］，可以得到二维波数的取值范围:

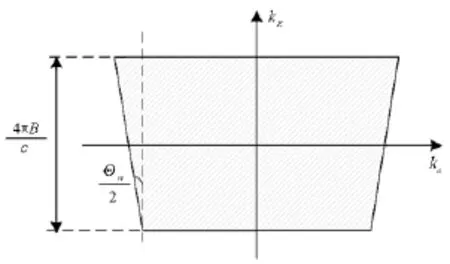
图2 线性SAR回波频谱支撑域Fig.2 Spectrum support domain of linear SAR

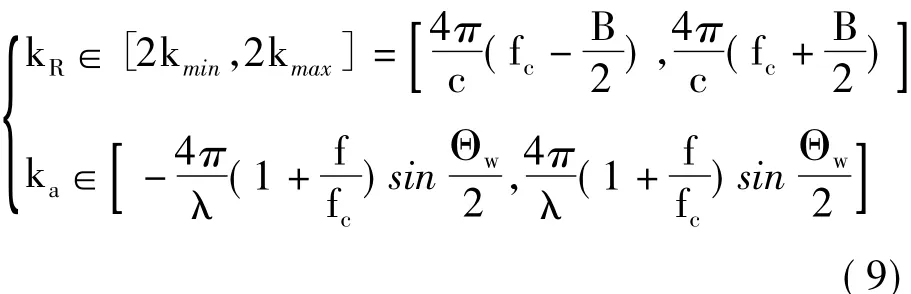
其中λ为载波波长。以距离向的频谱为例，其包络为矩形窗。基于傅里叶变换知识［14］，矩形窗函数的傅里叶变换对为sinc函数，即距离向点散布函数为sinc［πBt］，这表明距离向分辨率同信号带宽B相关，而点散布函数(Point Spread Function，PSF)对应的峰值旁瓣比、积分旁瓣比等均由sinc函数特性决定。类似地也可以得到方位向点散布函数的特性［14］。需要指出的是，线性SAR对应的回波频谱支撑域形状不会随着目标位置变化而变化，因而其点散布函数是唯一的。

针对单航过圆周SAR，设kx，ky分别表示目标P在x，y方向的波数。由式(4)得知圆周SAR的相位历程为Φc=

ρ的取值决定了圆周SAR在地平面波数支撑域的形状。观察式(11)得知ρ的取值同目标空间位置相关，即回波频谱支撑域的取值不再是恒定的，而是空变的。由此可知，单航过圆周SAR对应的频谱支撑域不再具有“方位不变性”且其点散布函数同样是空变的。

对于场景中心点，结合式(11)及式(12)，其频谱波数表示为kx=2k cosθzcosθ，ky=2k cosθzsinθ水平平面的径向波数ρ=2k cosθz。则地平面二维频谱支撑域呈标准圆环形，其中内圆的波数半径ρmin=2kmincosθz，外圆的波数半径ρmax=2kmaxcosθz。基于Hankel函数的傅里叶变换特性，半径为ρmax和ρmin的圆形频谱支撑域对应的傅里叶变换结果分别为和ρ，其中^r为水平面径向变量。由此得到标准圆环状频谱支撑域对应的点散布函数为:

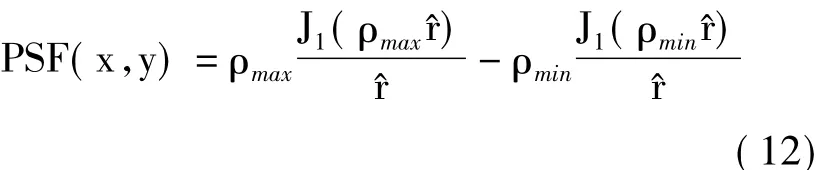
式(12)中J1(·)为1阶第一类贝塞尔函数。特殊地，当雷达发射的LFM信号的带宽为零，即为单频信号时，场景中心点对应的频谱支撑域由圆环变为圆周，且半径ρc=4πfccosθz/c。同样基于Hankel函数的傅里叶变换特性，得知此时场景中心点对应的点散布函数为:

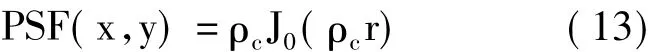
式(13)中J0(·)表示0阶第一类贝塞尔函数。由式(12)和式(13)可以得知圆周SAR工作模式下，目标二维分辨率同雷达波数相关，即同雷达发射电磁波的载频和带宽均有关，而不再仅仅取决于信号带宽，这是圆周SAR能够获取超高分辨率二维图像的原因。此外，圆周SAR对应的点散布函数特性，包括峰值旁瓣比、积分旁瓣比等，由贝塞尔函数特性决定，而不再是sinc函数。

然而，对于非场景中心点，人们难以得到其点散布函数的解析表达式，但可以采用数值分析的方法得到目标的点散布函数［15］。在圆周SAR的实际应用中，有必要对非场景中心点进行点散布函数的数值计算，以保证有效观测场景中所有目标具有相似的点散布函数特性。

2.3 单航过圆周SAR的三维成像能力

已知单航过线性SAR不具备高度维的分辨能力。而对于圆周SAR，基于单航过录取回波可以获取目标的高度信息。具体地，基于式(10)，可以得到圆周SAR工作模式下水平地面上目标P在高度维z的频谱分量:

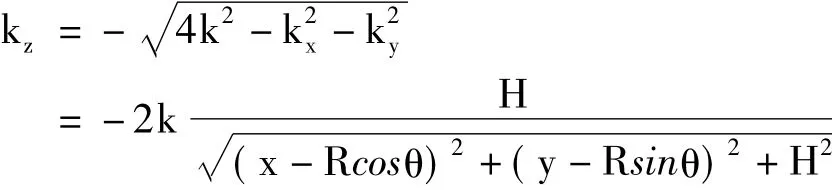
其中^θz(θ)表示目标P对应的雷达入射角。注意到^θz(θ)是观测角θ的函数，其变化范围可以如图3所示。

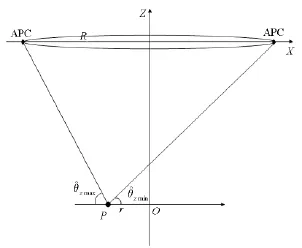
图3圆周SAR成像几何侧视图Fig.3 Side-view of the imaging geometry of CSAR

图3 给出了单航过圆周SAR雷达入射角的变化范围，图3中目标P距场景中心的径向距离为r，其对应的最大及最小雷达入射角分别为^θzmax和^θzmin:

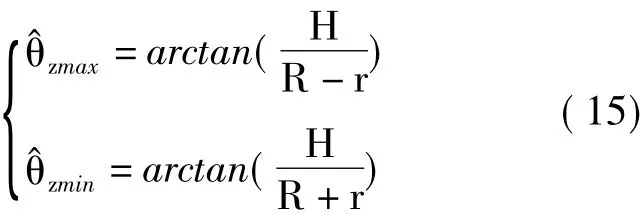
定义波数kz的带宽为Bz，观察式(14)，可知:

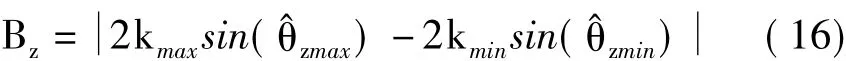
式(16)表明，对于非场景中心点，Bz始终大于零，故而无论雷达辐射信号为宽带信号或是单频信号，单航过圆周SAR对非场景中心点均具有高度维分辨能力。对于场景中心点，其对应的雷达入射角为恒定值θz。若雷达辐射信号为宽带信号且带宽为B，则场景中心点对应的高度维波数宽度为4πB sinθz/c，此时圆周SAR对其具有高度维分辨能力。若辐射信号为单频信号，则场景中心点对应的高度维波数宽度为零，圆周SAR对其不再具备高度维分辨能力。

经过本节分析，可以得到以下结论:

1)在雷达飞行高度及入射角确定的情况下，圆周SAR工作模式相比于线性SAR具有较小的观测范围；线性SAR的成像处理可以在斜距平面上进行；圆周SAR成像结果通常需要呈现在地平面，为正射成像处理。

2)线性SAR对应的点散布函数具有一致性，点散布函数特性由sinc函数决定；圆周SAR对应的点散布函数是空变的，其特性由贝塞尔函数决定。

3)线性SAR对应的频谱具有“方位不变性”，利于在多普勒域进行一致化处理以提高成像效率；单航过圆周SAR在水平地面对应的频谱支撑域是二维空变的，这为在频域开展高效率成像处理带来了挑战。

4)当雷达辐射信号为宽带信号时，单航过圆周SAR具备高度向分辨能力，但场景中不同径向距离处目标对应的高度向分辨率不同。

3 圆周SAR不同成像模型分析

在圆周SAR的成像特性中，如何克服空变频谱以提高圆周SAR频域成像处理效率已成为SAR领域的研究热点。对圆周SAR的成像模型进行调整，即可在频域进行一致化处理，进而提高频域成像算法的效率。本节分析了两种圆周SAR成像模型的调整方案。

3.1 平面圆周SAR

在H=0的情况下(或雷达运动平面等同于目标所在平面)，圆周SAR回波相位历史可以表示为:

观察得知此时水平地面的径向波数ρg=2k是一个恒定值，它表明此时圆周SAR在地平面的回波频谱支撑域是一个形状恒定的圆环，不再是空变的。因而此时圆周SAR的成像处理不再涉及空变处理，可以在频域进行一致化成像处理。但此时圆周SAR不再具备高度向分辨能力。总的来说，H=0条件下的圆周SAR具有相同的点散布函数且能够在频域进行快速成像处理，具有重要的理论意义。该成像模型不利于开展外场试验以实现大区域成像和监测，但在某些特殊领域具有重要意义，如医学成像以及高分辨率安检设备设计等方面。

3.2 沿不同高度平面的多航过圆周SAR

另一种更具有实际意义的圆周SAR模式即为多航过圆周SAR，图4给出了多航过圆周SAR的成像几何。

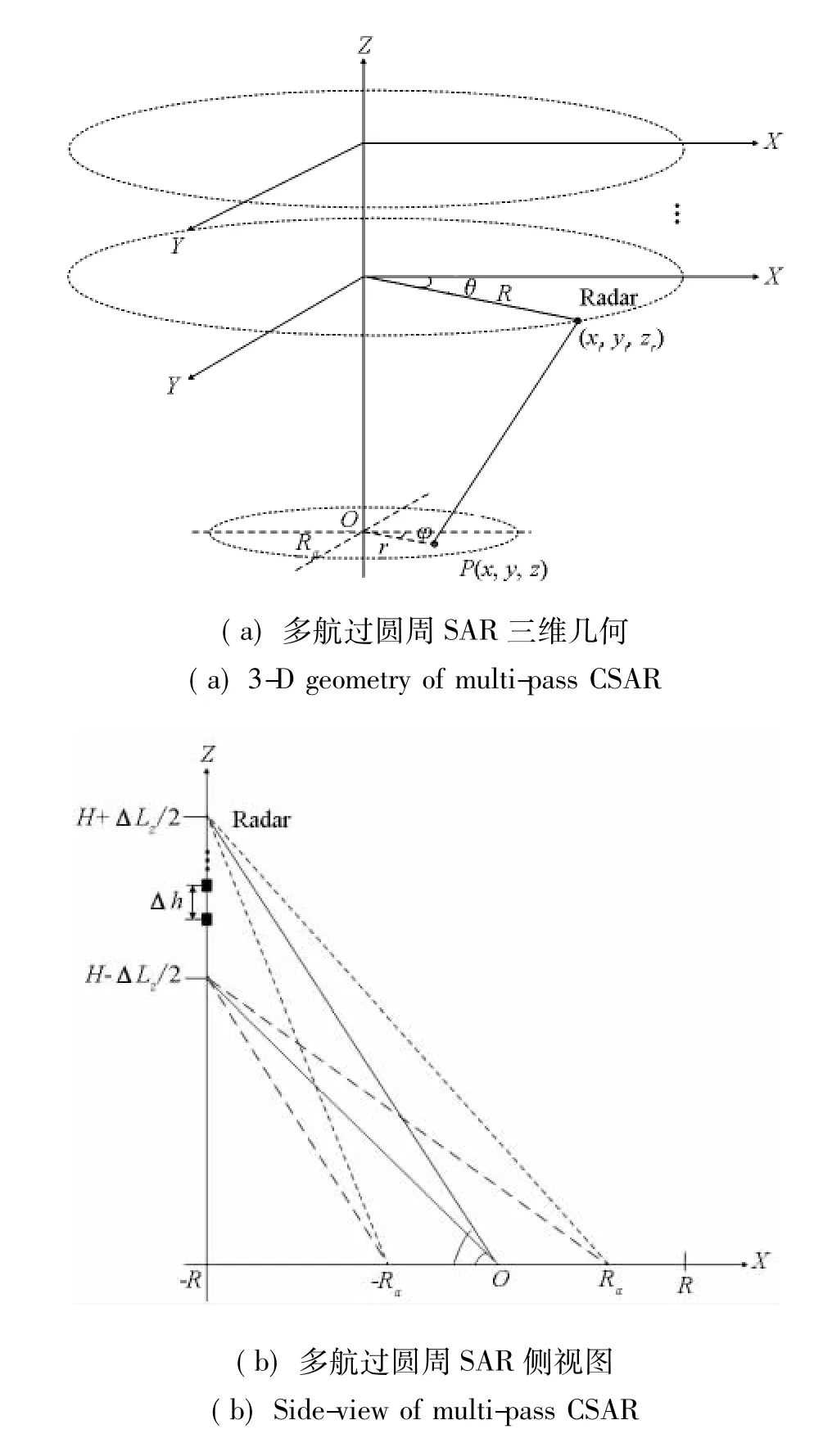
图4多航过圆周SAR成像几何Fig.4 Imaging geometry ofmulti-pass CSAR

图4 (a)为多航过圆周SAR成像示意图，图4(a)中参数定义同图1一致，只是雷达轨迹高度不再是恒定值H，而是多个等间隔排列的平行轨迹。不失一般性，此时目标P的坐标设为(x，y，z)。图4(b)为图4(a)的侧视图，高度维孔径长度为ΔLz，相邻两基线沿高度向的间隔为Δh。基于式(4)，对场景中任意非场景中心点目标P(x，y，z)，多航过圆周SAR对应的雷达回波可以表示为:

θc表示多航过圆周SAR模式下目标P处对应的雷达入射角，类似于图3，可以得到θc的变化范围，如图5所示。

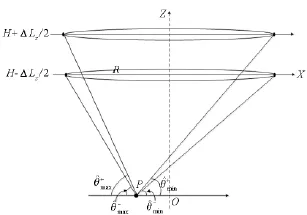
图5多航过圆周SAR雷达入射角示意图Fig.5 Incident angle according tomulti-pass CSAR

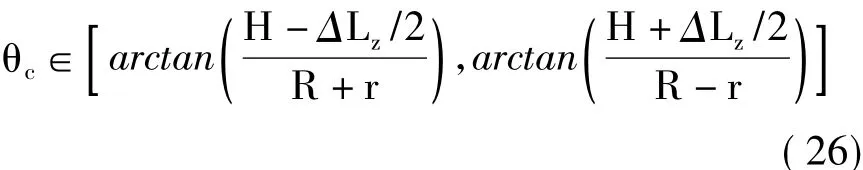
由此得到多航过圆周SAR对应的高度维波数宽度为:

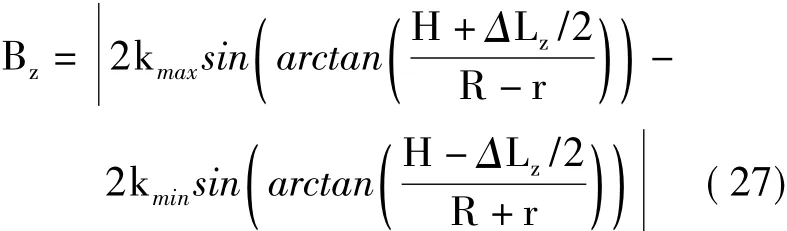
对比式(27)和式(16)，可知多航过圆周SAR对应的高度维波数宽度一直大于单航过圆周SAR，且无论发射信号为宽带信号还是单频信号，多航过圆周SAR对观测场景中任意位置的目标均具备高度维分辨能力。

观察式(27)，可以得知场景边缘处对应更大的高度维波数宽度，由此得到整个观测场景中高度维波束宽度的最大值为:

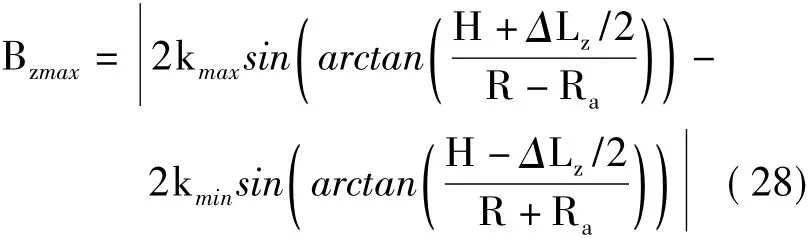
其对应的高度维采样间隔为2π/Bzmax，为避免高度维的混叠，对于多航过圆周SAR，其基线采样间隔需满足:

紧接着，对式(24)中的信号进行角度域的傅里叶变换，可以得到:

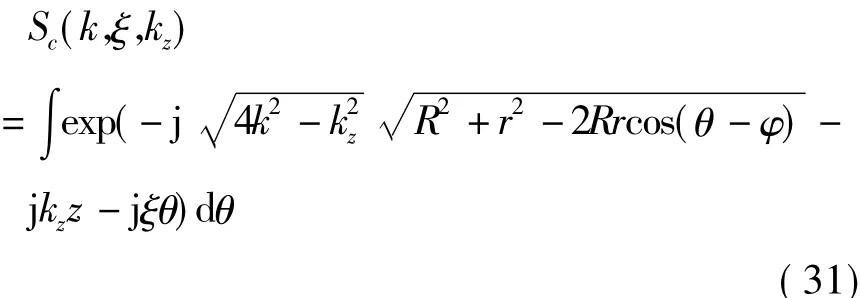
其中ξ表示角度域波数。基于驻定相位原理，可以通过求解式(32)来得到驻定相位点。

式(35)给出了多航过圆周SAR的三维频谱表达式。观察发现圆周SAR三维频谱由两部分叠加而成。这是由于圆周SAR角度域频谱变换中对应两个驻定相位点造成的。对于式(35)，构造匹配滤波函数: Hc(k，ξ，kz)

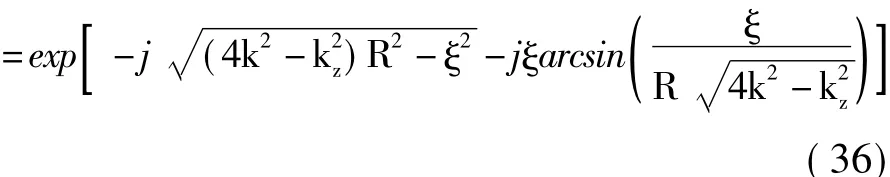
观察发现式(36)中匹配滤波函数同目标所在位置无关，是非空变的(这有利于在频域进行一致化处理，提高成像效率)。经匹配滤波后，得到:

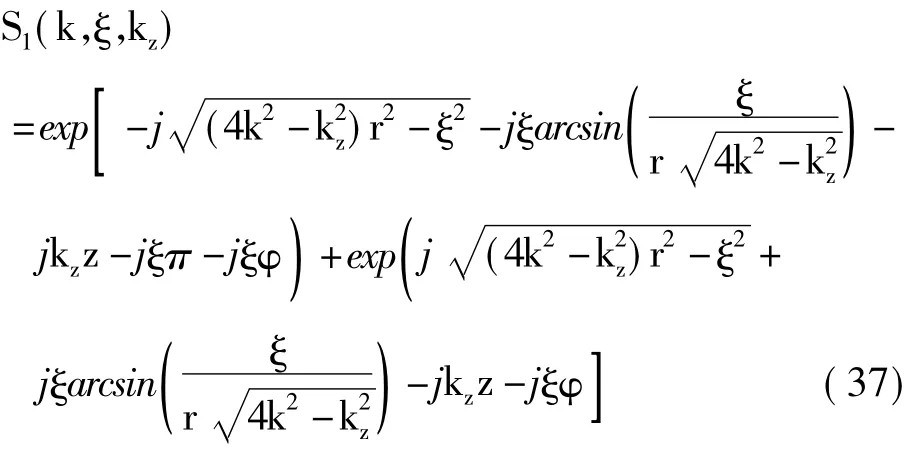
定义2kρ=并对式(37)进行角度域傅里叶逆变换，得到:

式(40)中三个指数项分别决定了目标在成像处理后的位置。对S3(kx，ky，kz)进行三维逆傅里叶变换，即可得到精确的圆周SAR三维成像结果。

事实上，类似于对式(10)的分析，多航过圆周SAR观测场景中不同目标的点散布函数仍是不同的。但在高度维频率域，却可以开展一致化匹配滤波，这大大提高了成像效率。

3.3 多航过圆周SAR仿真结果

鉴于多航过圆周SAR成像模式具有重要的实际应用价值，这里利用计算机仿真对其成像流程做出验证。三维成像处理运算量十分巨大，为减小运算量，选用小尺度的圆周SAR成像几何，具体参数见表1。

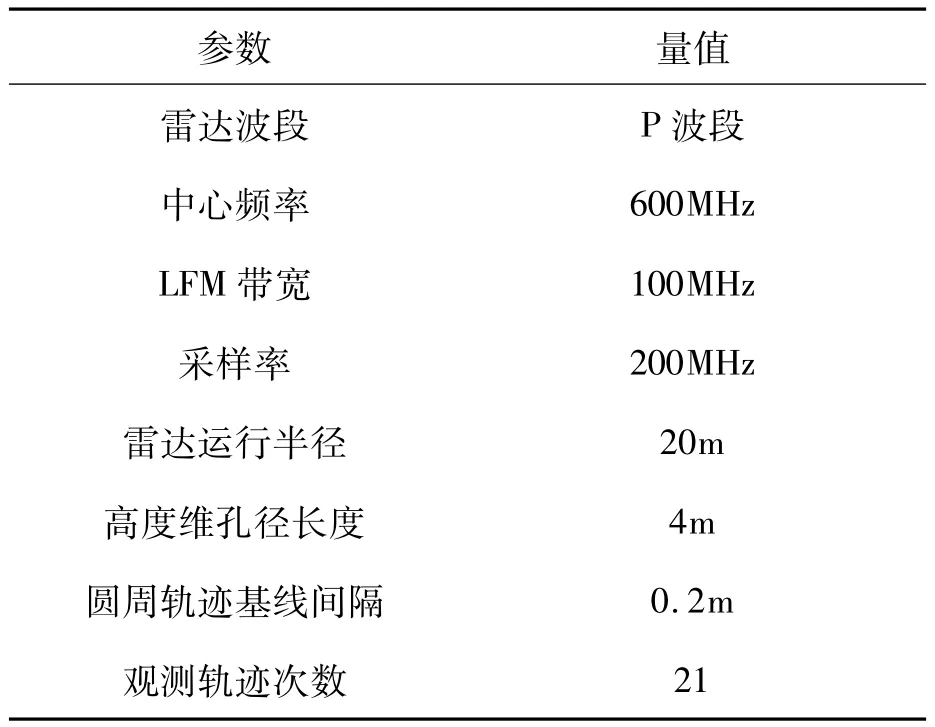
表1 多航过圆周SAR仿真参数设置Tab.1 Parameters ofmulti-pass CSAR

在场景布置方面，在观测场景内布置三个散射点，其三维坐标分别为(0，0，0)，(0，-0.5，1)和(0，0.5，-1)，单位均为m。利用3.2节阐述的成像处理方法，可以得到如图6所示成像结果。

图6给出了多航过圆周SAR对点目标的成像结果。图6(a)给出了三个点目标的三维成像结果，由于三维图像不易表达，针对点目标(0，0.5，-1)，分别沿y-z平面及x-y平面进行剖切，得到了其点散布函数在y-z平面及x-y平面的剖面图，分别如图6(b)及图6(c)所示。更进一步地，可以得到点散布函数沿x向，y向及z向的剖面图，分别如图6(d)、图6(e)、图6(f)所示。具体地，对点散布函数的特性进行了测量，得到了如表2所示的测量结果。

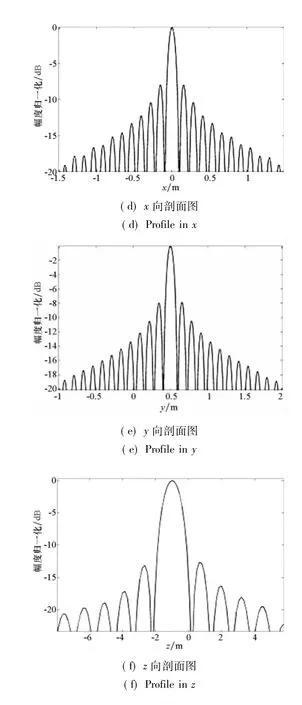
图6 多航过圆周SAR成像结果Fig.6 Imaging results ofmulti-pass CSAR

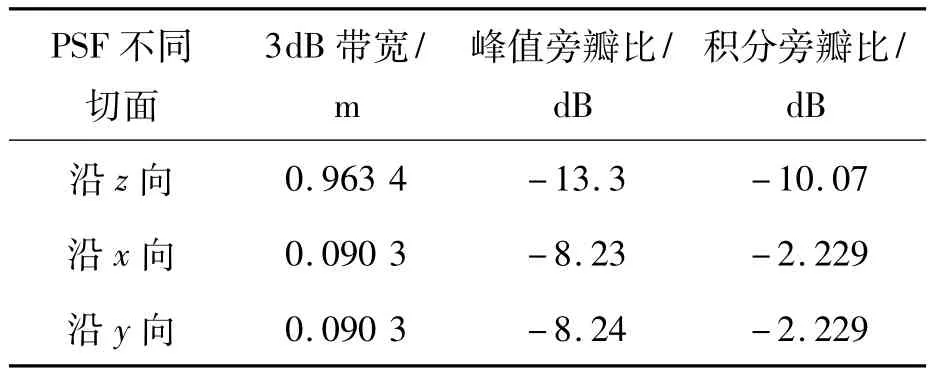
表2 目标点散布函数分析Tab.2 Quantitative analysis of point target

本节的分析及数值仿真表明，理论上，H=0圆周SAR以及多航过圆周SAR的频域成像处理是精确高效的。但在实际应用中，单航过/多航过圆周SAR面临的挑战包括运动误差、不同轨迹间非均匀间隔以及观测轨迹次数较少等因素。鉴于这些挑战同本文主旨有所区别，作者将在其他文章中对上述实际问题给出相应的处理方法。

4 结论

本文建立了圆周SAR信号模型，基于理论分析对比了圆周SAR同线性SAR在成像处理中的差异，凸显了圆周SAR的成像特性，包括二维超高分辨率、三维成像能力等；得知了圆周SAR对应的点散布函数是空变的，其频域成像处理的难点在于空变频谱不便于进行一致化处理，成像效率低。分析了平面CSAR和多航过CSAR两种成像模式，从理论上严格证明了这两种成像模式便于在频域开展一致化处理，成像效率高。该分析有助于了解圆周SAR成像特性并进一步地开发高效精确的圆周SAR频域成像方法。

References)

［1］Soumekh M.Synthetic aperture radar signal processing with matlab algorithms［M］.USA:Wiley-Interscience，1999: 486-552.

［2］Ishimaru A，Chan T K，Kuga Y.An imaging technique using confocal circular synthetic aperture radar［J］.IEEE Transactions on Geoscience and Remote Sensing，1998，36(5):1524-1530.

［3］Lin Y，HongW，Tan W X，etal.Extension of rangemigration algorithm to squint circular SAR imaging［J］.IEEE Geoscience and Remote Sensing Letters，2011，8(4):651-655.

［4］闵锐.机载SAR三维成像理论及关键技术研究［D］.成都:电子科技大学，2008.MIN Rui.Research on airborne SAR three-dimensional imaging theory and key technology［D］.Chengdu:University of Electronic Science and Technology of China，2008.(in Chinese)

［5］刘燕.高分辨率及新模式SAR成像算法研究［D］.西安:西安电子科技大学，2012.LIU Yan.Study on high-resolution SAR and new type SAR imaging［D］.Xi'an:XiDian University，2012(in Chinese).

［6］刘燕，吴元，孙光才，等.圆轨迹SAR快速成像处理［J］.电子与信息学报，2013，35(4):852-858.LIU Yan，WU Yuan，SUN Guangcai，et al.Fast imaging processing of circular SAR［J］.Journal Electronics＆Information Technology，2013，35(4):852-858.(in Chinese)

［7］Frolind P，Gustavsson A，Lundberg M，et al.Circular-aperture VHF-band synthetic aperture radar for detection of vehicles in forest concealment［J］.IEEE Transactions on Geoscience and Remote Sensing，2012，50(4):1329-1339.

［8］Palm S，Oriot H M，Cantalloube H M.Radargrammetric DEM extraction over urban area using circular SAR imagery［J］.IEEE Transactions on Geoscience and Remote Sensing，2012，50(11):4720-4725.

［9］Ponce O，Prats-Iraola P，Pinheiro M，et al.Fully polarimetric high-resolution 3-D imaging with circular SAR at l-band［J］.IEEE Transactions on Geoscience and Remote Sensing，2014，52(6):3074-3090.

［10］Ponce O，Prats P，Scheiber R，etal.Study of the3-D impulse response function of holographic SAR tomography with multicircular acquisitions［C］//Proceedings of 10th European Conference on Synthetic Aperture Radar，EUSAR，2014: 1-4.

［11］Ponce O，Prats-Iraola P，Scheiber R，et al.Polarimetric 3-D reconstruction from multicircular SAR at P-band［J］.IEEE Geoscience and Remote Sensing Letters，2014，11(4):803-807.

［12］洪文.圆迹SAR成像技术研究进展［J］.雷达学报，2012， 1(2):124-135.HONGWen.Progress in circular SAR imaging technique［J］.Journal of radars，2012，1(2):124-135.(in Chinese)

［13］林赟，谭维贤，洪文，等.圆迹SAR极坐标格式算法研究［J］.电子与信息学报，2010，32(12):2802-2807.LIN Yun，TAN Weixian，HONG Wen，et al.Polar format algorithm for circular synthetic aperture radar［J］.Journal of Electronics＆Information Technology，2010，32(12): 2802-2807.(in Chinese)

［14］保铮，邢孟道，王彤.雷达成像技术［M］.北京:电子工业出版社，2005.BAO Zheng，XING Mengdao，WANG Tong.The technology of radar imaging［M］.Beijing:Publishing House of Electronics Industry，2005.(in Chinese)

［15］Prats-Iraola P，Rodriguez-Cassola M，De Zan F，et al.Efficient evaluation of fourier-based SAR focusing kernels［J］.IEEE Geoscience and Remote Sensing Letters，2014，11(9):1489-1493.

Comparison and analysis of the imaging properties between circular SAR and linear SAR

JIAGaowei，CHANGWenge
(College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China)

With its intrinsic characteristics，circular synthetic aperture radar has lately become a particular interest to the radar community.The differences of imaging processing between the circular synthetic aperture radar and linear trajectory synthetic aperture radarwere compared and analyzed.The detailed comparisons containing the size of the observed area，the properties of the point spread function，and the properties of echo spectrum were carried out.Itwas learnt that the difficulty of the imaging processing of single-pass circular synthetic aperture radar lies on its space dependence.To overcome this difficulty，the plane circular synthetic aperture radar and multi-base line circular synthetic aperture radar imaging models were analyzed.Simulation testwas carried out and the corresponding results prove the proposed analysis is valid.

circular synthetic aperture radar；linear synthetic aperture radar；echo spectrum；point spread function；three dimensional imaging

TN957

A

1001-2486(2015)05-161-08

10.11887/j.cn.201505025

http://journal.nudt.edu.cn

2014-11-26

国家自然科学基金资助项目(61501477)

贾高伟(1989—)，男，河南周口人，博士研究生，E-mail:ji_as@126.com；常文革(通信作者)，男，教授，博士，博士生导师，E-mail:changwenge@nudt.edu.cn