改进多重信号分类算法的宽带频谱快速感知方法*

孙伟朝，王丰华，黄知涛，王翔(国防科技大学电子科学与工程学院，湖南长沙410073)

改进多重信号分类算法的宽带频谱快速感知方法*

孙伟朝，王丰华，黄知涛，王翔
(国防科技大学电子科学与工程学院，湖南长沙410073)

针对宽带频谱感知中采样率大、感知时间长的问题，在调制宽带转换器采样的基础上提出了一种改进多重信号分类算法的宽带频谱快速感知方法。调制宽带转换器对宽带频谱进行欠奈奎斯特采样，以最小描述长度准则估计信号个数，用改进多重信号分类谱估计信号位置。算法引入调整因子，使得多重信号分类谱中信号位置更为明显，降低了噪声的干扰。整个感知过程无须重构原始波形，无须计算频谱，大大降低了计算量，而且感知算法计算复杂度低，提高了感知效率。仿真结果表明，在低信噪比的情况下，该算法仍具有很好的检测性能。

宽带频谱快速感知；欠奈奎斯特采样；调制宽带转换器；多重信号分类算法

频谱感知广泛应用于认知无线电［1-2］、无线电监测与频谱管理等领域。随着现代通信技术的发展，宽带信号逐步成为一种常见的信号形式。对宽带频谱进行感知，过高的采样率和过大的数据量，对现有的模数转换器(Analog to Digital Converter，ADC)、处理器和存储设备等提出了巨大的挑战。

近年来，Mishali等提出的调制宽带转换器(Modulated Wideband Converter，MWC)系统［3］，以宽带频谱的稀疏性和压缩感知(Compressed Sensing，CS)理论［4］为基础，用远低于奈奎斯特采样速率的速率进行采样，可无损重构信号。该系统易于实现，硬件要求低，并能达到Landau最小采样速率［5］，因此，是一种有效的解决宽带频谱采样率过大问题的方案。

文献［6］利用欠奈奎斯特采样值重构平稳信号的功率谱，进行宽带频谱感知；文献［7］建立了一种空频2维压缩感知模型，提出相应的重构算法，通过寻找空间小波基的方法检测信号；文献［8-9］利用不同的重构算法对压缩后的信号进行重构，得到信号的功率谱。这些方法大都是通过重构接收信号，计算功率谱进行频谱感知。重构信号算法复杂度较高、运算量较大，用于频谱感知会引起较大的感知延迟。例如，认知无线电中出现感知延迟，甚至有可能给主用户造成干扰。

文献［10］利用多重集采样提出了一种宽带频谱感知方法，直接在时域利用MUSIC算法实现频谱感知。文献［11］也利用多重集采样，基于多重信号分类(Multiple Signal Classification，MUSIC)算法提出了一种动态门限搜索匹配的信号个数估计方法。但基于多重集采样的方法，要求时间延迟部分精确到其奈奎斯特采样周期量级，对于宽带频谱采样来说，保持各支路之间的精确时延是很困难的。

针对上述存在的问题，孙伟朝等在易于实现的MWC进行欠奈奎斯特采样的基础上提出了基于改进MUSIC算法的宽带频谱快速感知方法。

1 问题描述

稀疏多带信号是军事和民用通信领域经常遇到的信号类型［13］。假设接收信号x(t)是一个稀疏多带信号，带宽范围为［-fnyq/2，fnyq/2］，fnyq是其奈奎斯特采样速率。其频谱是由q个互不相交的子带Xi(f)(i=1，…，q)及对称的负频段子带组成，如图1所示。所有子带中的最大的带宽为B，子带最大个数N(N≥2q)，且有所有子带带宽之和远小于信号的奈奎斯特频率。

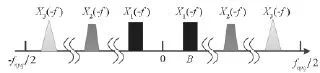
图1 稀疏多带信号频谱Fig.1 Sparsemultiband signal spectrum

整个频带等宽度划分为L个连续的窄带信道，每个信道宽度不小于B，信道序号为［1，…，L］。各子带Xi(f)所处的信道序号组成的集合称为支撑集［3］。

问题描述如下:预先不知道宽带频谱中信号子带位置的情况下，如何利用MWC得到的压缩采样点快速感知子带所处信道序号，即快速估计出支撑集。

2 MWC欠奈奎斯特采样

MWC采样结构如图2所示，共有m个通道，每个通道都包括一个混频器、一个低通滤波器和一个ADC。接收到的信号x(t)同时输入到m个通道，乘上一个周期Tp=1/fp的伪随机周期序列波形pi(t)，fp为周期序列波形的频率，且每路的伪随机序列互不相关。经过截止频率为1/2Ts的低通滤波器滤波，和采样率fs=1/Ts的ADC采样，得到压缩采样点yi［n］。

周期序列波形pi(t)按傅里叶级数展开［3］有

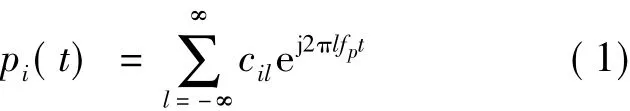
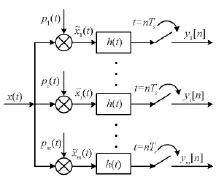
图2 MWC结构Fig.2 MWC structure

文献［3］中定理2给出了式(3)有唯一最稀疏解的充分条件。其中，要求m×L的系数矩阵A中任意2N列线性独立。

式(3)表示了压缩采样序列yi［n］与原始信号x(t)之间的关系，以及一个求欠定方程组最稀疏解的问题。在感知过程中，文献［3］提出了连续到有限(Continue To Finite，CTF)模块，把式(3)转化为多观测矢量(Multiple Measurement Vectors，MMV)模型，再利用压缩感知稀疏重构算法求解频率支撑集，如复杂度低、运行速度快的正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法［14］等。

3 宽带频谱快速感知算法

MUSIC算法是阵列信号处理中经典的信号参数估计方法。孙伟朝等本文借助阵列信号处理模型，对MUSIC算法进行改进，引入调整因子，比MUSIC算法具有更高的感知正确率。为表述方便，本文算法记为MUSIC_M。

3.1 子空间分析

根据式(3)，可得到带噪声的观测序列y［n］的频域表达式

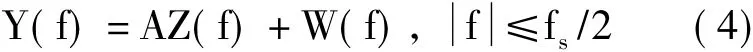
其中W(f)代表高斯噪声，其分布为N(0，σ2wI)，且与信号不相关。

观测矢量的自相关矩阵

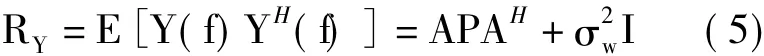
其中，E［·］是求期望，H表示共轭转置，P是信号矢量的自相关矩阵。对RY进行特征值分解，得到信号子空间Es和噪声子空间En。

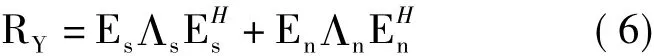
其中，Λs和Λn分别表示由信号和噪声的特征值构成的对角阵，Es和En是对应的特征向量矩阵。假定观测长度为K，自相关矩阵RY可通过式(7)估计。

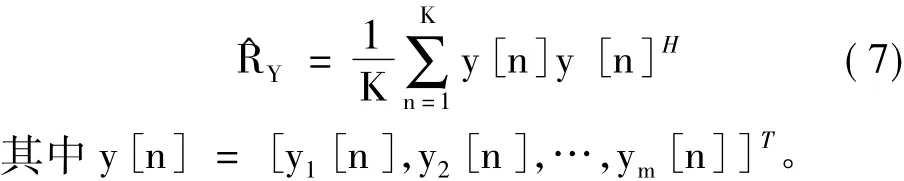
信号个数估计采用最小描述长度(Minimum Description Length，MDL)准则，MDL准则在决策过程中不需要人工参与，能够直接利用观测矢量计算出所含有的信号数目［12］，即信号个数的估计值q^。

3.2 改进的MUSIC算法

估计出信号个数q^之后，m-q^个小特征值即为噪声的特征值，对应的噪声特征向量矩阵E^n是其噪声子空间。MUSIC算法公式［10］为

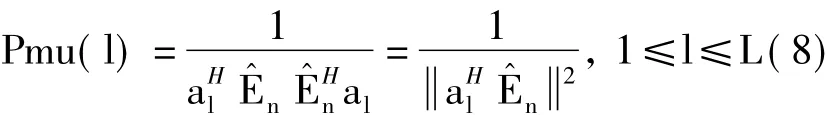
其中，·表示2范数，l是信道序号，al表示系数矩阵A的第l列。

由式(1)可得知，系数矩阵A与窄带远场信号的波达方向(Direction of Arrival，DOA)数学模型中的系数矩阵存在差异，矩阵各元素的模不恒定。因此，直接计算MUSIC谱易受到“噪声”干扰。而整个空间(噪声子空间和信号子空间)的MUSIC谱中包含了所有“噪声”信息，可以用来

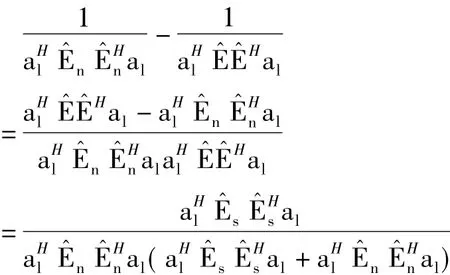
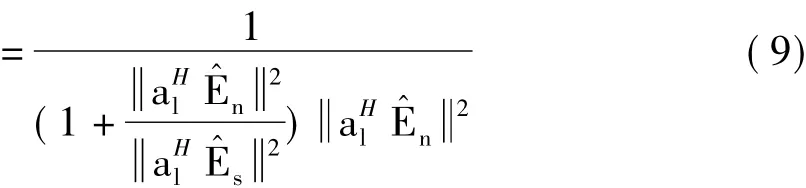
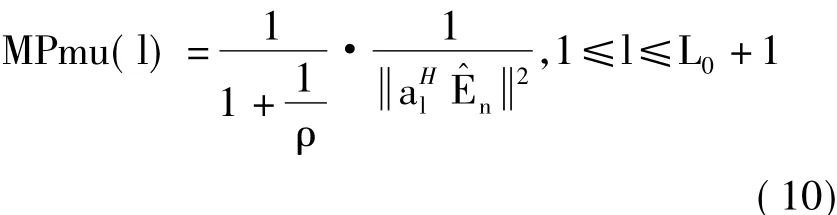
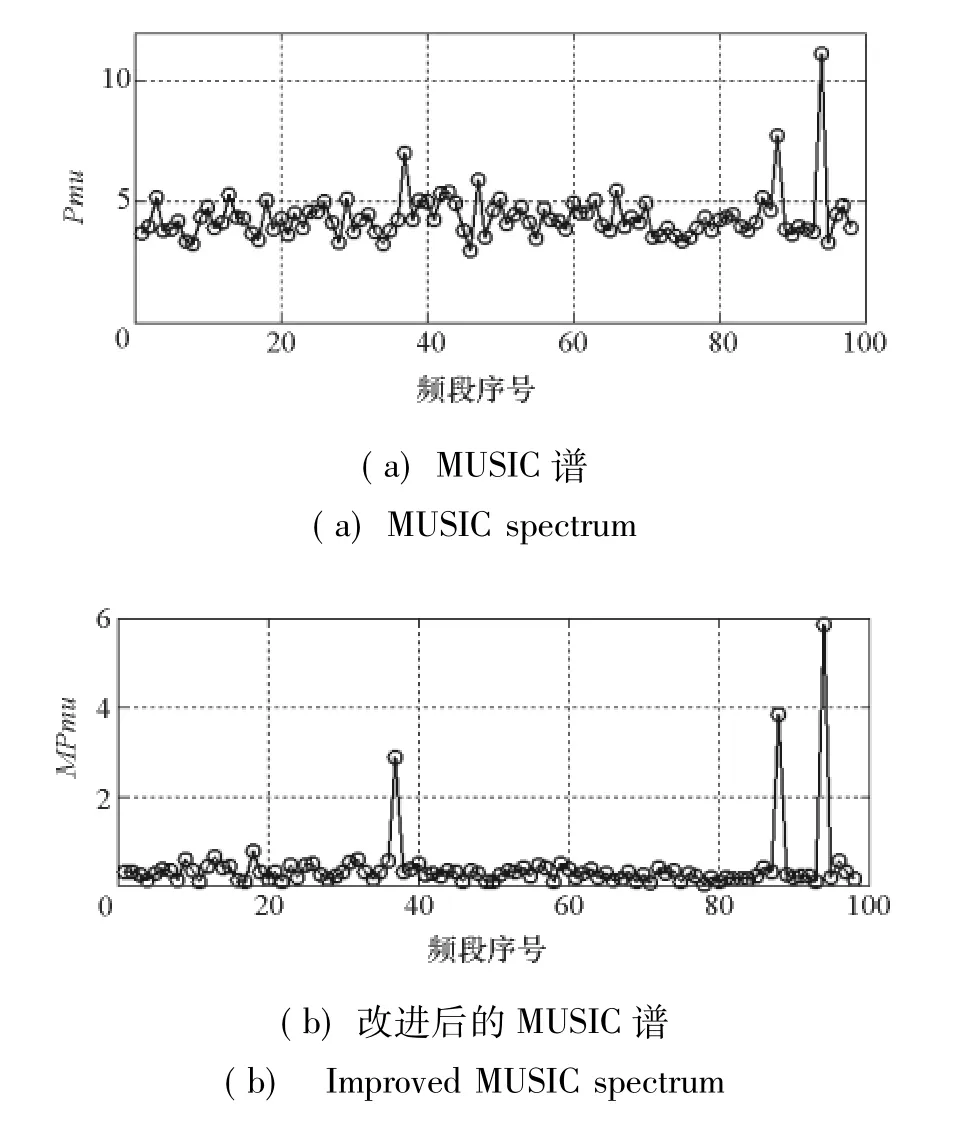
图3 信号支撑集为{37，88，94}时的MUSIC谱和改进后的MUSIC谱Fig.3 MUSIC spectrum and improved MUSIC spectrum with frequency support{37，88，94}

MUSIC_M算法的主要步骤为:

1)利用MWC对宽带模拟信号采样，得到压缩采样序列y［n］；

3)进行特征值分解，特征值按从大到小排序，得到特征值d和对应的特征向量矩阵E；

4)利用MDL准则估计信号个数^q；

5)利用式(10)计算谱MPmu；

3.3 算法复杂度分析

文献［15］也提出了基于MWC采样的宽带频谱感知方法。利用MDL准则估计信号个数，应用OMP算法感知频谱。下面把基于OMP的感知算法与MUSIC_M算法在计算复杂度方面进行分析比较。

3.3.1 基于OMP算法的宽带频谱感知复杂度分析

基于OMP算法的宽带频谱感知方法与MUSIC_M算法的计算量差异主要体现在OMP算法上。下面在文献［16］的基础上分析上述OMP算法的复杂度。

在第t次迭代中，OMP算法中计算选取与残差相关性最强的列的集合的复杂度为O(mLK)；然后更新残差Res(t)=V-(，Moore-Penrose伪逆()†=［(，维数为m×2t。而2t×2t的复矩阵求逆至少需要O［(2t)3］的计算量，那么上述求残差过程的计算复杂度为O［m(2t)K+m(2t)2+(2t)3］。因此，OMP算法中第t次迭代的计算复杂度为O［mLK+m(2t)K+m(2t)2+(2t)3］。

3.3.2 MUSIC_M算法复杂度分析

MUSIC_M算法与OMP算法相比，计算量的主要差别在于计算谱MPmu上。

谱MPmu共需计算L0+1=(L+1)/2个值，每个值中的计算复杂度为O(2m2+m)，的复杂度为O［2m(m-q^)+m］。那么，+1点的计算复杂度O［(L+1)(2m2+mmq^)］。可以看出，信号个数越多，计算量越小；当q^=1时，计算量最大，计算复杂度为O［2(L+1) m2］。根据文献［3］要求m≥4q^才能全盲恢复信号，当q^=m/4时那么L0+1点的计算复杂度的乘法次数最少，约为O［(L+1)(7/4m2+m)］。

3.3.3 算法复杂度比较

基于上述分析，表1给出了两种方法的计算复杂度比较。

表1 两种感知算法计算复杂度比较Tab.1 Computational complexity comparison of two sensingmethods

MWC中，L＞m≥4^q，采样长度K≥m。当^q≥2时，OMP算法的复杂度高于MUSIC_M算法，且随着信号个数的增加，其复杂度也会快速增加；而MUSIC_M算法的复杂度会随着信号个数的增加而降低。一般宽带频谱中的信号个数都会多于1个，因而，应用MUSIC_M算法比OMP算法能快速感知频谱。

4 仿真实验

稀疏多带信号由式(1)模型产生［10］。

其中:si(t)～N(0，实验中假设所有信号功率相同，即=σ2；h(t)为窄带低通滤波器；q表示信号个数；w(t)～N(0，)为加性高斯白噪声，带内信噪比SNR=σ2/。

设置信号的有效带宽范围为［0，500MHz］，即fnyq=1GHz，信号个数q=3，谱带数目N=6，选取通道数m=30，采样长度K=101；载频fi随机产生，各信号互不交叠，每个信号带宽都为B= 5MHz，选取信道数L=195。则每个通道的采样率fs=fnyq/L=5.13MHz，平均采样率mfs= 153.9MHz，只有奈奎斯特采样率的15.4%，大大降低了采样率，实现了低速采样。

每个信噪比下进行500次蒙特卡洛仿真实验，以式(12)～(13)所示的估计值的检测概率和虚警概率分析算法性能［15］。

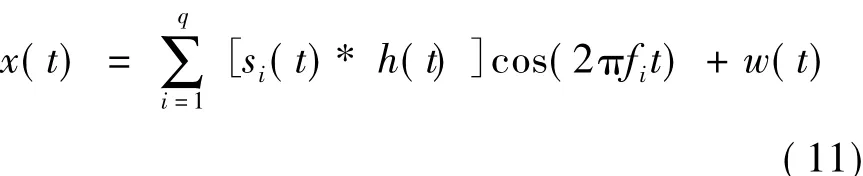
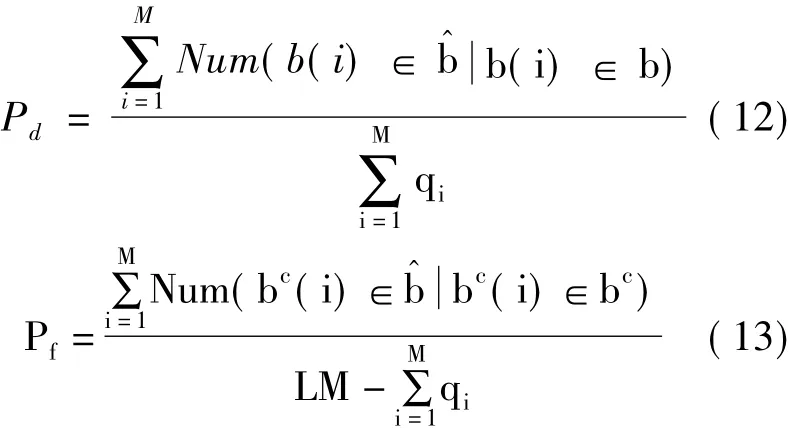
其中:qi表示第i次实验产生的信号个数；Num(b(i)b(i)∈b)表示一次实验中，实际支撑集b与估计支撑集中相同元素的个数；Num((i)∈i)∈bc)表示一次实验中，实际支撑集的补集bc与估计支撑集中相同元素的个数。

图4和图5分别给出了在不同信噪比下MUSIC_M，MUSIC和OMP算法的检测概率曲线和虚警概率曲线。由图4、图5可见:同信噪比下，MUSIC_M算法的检测概率比MUSIC算法的高，并且在15dB时接近于1；其虚警概率比MUSIC算法的低，并且在15dB时接近于0。同信噪比下，MUSIC_M算法的检测概率和OMP算法的基本一样，虚警概率也基本一样。

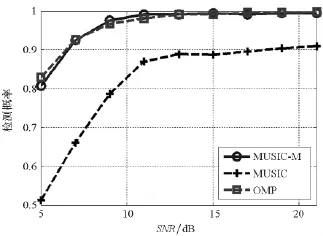
图4 MUSIC_M，MUSIC，OMP算法检测概率比较Fig.4 Detection probability comparisons between MUSIC_M，MUSIC and OMP

图6 给出了信号个数q从1增加到6时，MUSIC_M算法与OMP算法在所用的平均时间。从图6中可以看出，在信号个数多于1时，MUSIC_M算法的处理时间远低于OMP算法，而且不随信号个数的增加而增加。

5 结论

本文采用MWC采样来解决宽带频谱感知中的采样率过高和多重集采样等硬件难以实现等问题；用MDL准则估计信号个数，并引入调整因子改进MUSIC谱估计算法，来估计信号的支撑集，从而完成宽带频谱感知。与基于OMP的感知算法相比，MUSIC_M算法在不损失感知正确率的基础上，大大降低了算法复杂度，减少了感知时间，实现了宽带频谱快速感知。

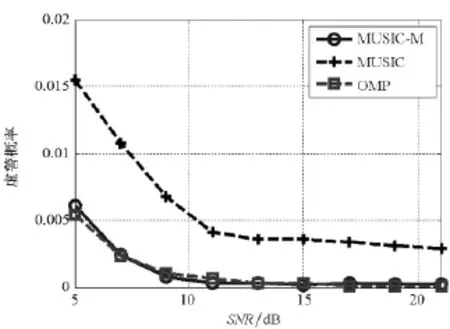
图5 MUSIC_M，MUSIC，OMP算法虚警概率比较Fig.5 False alarm probability comparisons between MUSIC_M，MUSIC and OMP

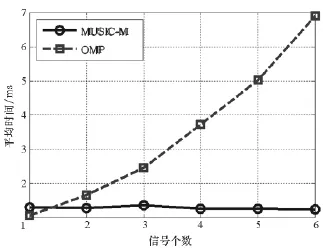
图6 信号数不同时MUSIC_M与OMP算法耗时比较Fig.6 Average time comparisons between MUSIC_M and OMP

References)

［1］Bao D，Vito L D，Rapuano S.A histogram-based segmentation method for wideband spectrum sensing in cognitive radios［J］.IEEE Transactions on Instrumentation and Measurement，2013，62(7):1900-1908.

［2］Sharma S K，Chatzinotas S，Ottersten B.Compressive sparsity order estimation for wideband cognitive radio receiver［J］.IEEE Transactions on Signal Processing，2014，62(19):4984-4996.

［3］Mishali M，Eldar Y C.From theory to practice:sub-Nyquist sampling of sparsewideband analog signals［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4(2):375-391.

［4］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［5］Landau H J.Necessary density conditions for sampling and interpolation of certain entire functions［J］.Acta Mathematica，1967，117(1):37-52.

［6］Cohen D，Eldar Y C.Sub-nyquist sampling for power spectrum sensing in cognitive radios:a unified approach［J］.IEEE Transactions on Signal Processing，2014，62(15): 3897-3910.

［7］王韦刚，杨震，胡海峰.一种宽带频谱检测的空域频域压缩感知方法［J］.电子与信息学报，2013，35(2): 255-260.WANGWeigang，YANG Zhen，HU Haifeng.A method of space-frequency compressed sensing on wideband spectrum detection［J］.Journal of Electronics＆Information Technology，2013，35(2):255-260.(in Chinese)

［8］Zhang Z H，Li H S，Yang D P，et al.Space-time Bayesian compressed spectrum sensing for wideband cognitive radio networks［C］//Proceedings of IEEE Symposium on New Frontiers in Dynamic Spectrum，2010:1-11.

［9］Wang Y，Pandharipande A，Leus A.Compressive sampling based MVDR spectrum sensing［C］//Proceedings of 2010 2nd International Workshop on Cognitive Information Processing，2010:333-337.

［10］Rashidi M，Haghighi K，Owrang A，et al.A wideband spectrum sensingmethod for cognitive radio using sub-Nyquist sampling［C］//Proceedings of Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop，2011:30-35.

［11］赵知劲，张鹏，尚俊娜，等.基于MUSIC算法的宽带频谱感知［J］.计算机工程，2012，38(13):83-92. ZHAO Zhijin，ZHANG Peng，SHANG Junna，et al.Wideband spectrum sensing based on MUSIC algorithm［J］.Computer Engineering，2012，38(13):83-92.(in Chinese)

［12］Wax M，Kailath T.Detection of signals by information theoretic criteria［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1985，33(2):387-392.

［13］杨鹏，樊昀，黄知涛，等.基于Sub-Nyquist采样的单通道频谱感知技术［J］.国防科技大学学报，2013，35(4): 121-127.YANG Peng，FAN Yun，HUANG Zhitao，et al.Singlechannel spectrum sensing technique based on sub-Nyquist sampling［J］.Journal of National University of Defense Technology，2013，35(4):121-127.(in Chinese)

［14］Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2007，53(12):4655-4666.

［15］赵知劲，张鹏，王海泉，等.基于OMP算法的宽带频谱感知［J］.信号处理，2012，28(5):723-728.ZHAO Zhijin，ZHANG Peng，WANG Haiquan，et al.Wideband spectrum sensing based on OMP algorithm［J］.Signal Processing，2012，28(5):723-728.(in Chinese)

［16］Sturm B L，Christensen M G.Comparison of orthogonal matching pursuit implementations［C］//Proceedings of 20th European Signal Processing Conference，2012:220-224.

W ideband spectrum fast sensing method based on improved multip le signal classification

SUNWeichao，WANG Fenghua，HUANG Zhitao，WANG Xiang
(College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China)

Aiming at the problem of exorbitant sampling rate and sensing time too long in wideband sensing，a wideband spectrum sensing method using improved multiple signal classification(MUSIC)based onmodulated wideband converter(MWC)was proposed.The MWC for sub-Nyquist sampling was used，the number of signals byminimum description length(MDL)criterion was estimated，and the signals’location using improved MUSIC was estimated.In the improved MUSIC，an adjustment factor was given，which enhanced the MUSIC spectrum at the signal’locations and reduced others，and the noise jam was restrained.An amount of calculations was reduced，because it neither needed to recover original wave，nor calculated PSDs in the whole process.The complexity of sensingmethod was small，so that it increased sensing efficiency.The results show a reliable detection even in low signal noise ratio.

wideband spectrum fast sensing；sub-Nyquist sampling；modulated wideband converter；multiple signal classification

TN911.7

A

1001-2486(2015)05-155-06

10.11887/j.cn.201505024

http://journal.nudt.edu.cn

2014-12-09

国家自然科学基金资助项目(61302141)

孙伟朝(1986—)，男，河南夏邑人，博士研究生，E-mail:sweichao1266@163.com；黄知涛(通信作者)，男，教授，博士，博士生导师，E-mail:taldcn@sina.com