正交频分复用/偏移正交振幅调制半盲信道估计*

李啸天，雷菁，刘伟，曹伟，李艳斌(.中国电子科技集团公司第五十四研究所，河北石家庄05008；.国防科技大学电子科学与工程学院，湖南长沙40073)

正交频分复用/偏移正交振幅调制半盲信道估计*

李啸天1，2，雷菁2，刘伟2，曹伟2，李艳斌1
(1.中国电子科技集团公司第五十四研究所，河北石家庄050081；2.国防科技大学电子科学与工程学院，湖南长沙410073)

非合作通信背景下，针对传统干扰近似法(IAM)进行正交频分复用(OFDM)/偏移正交振幅调制(OQAM)系统信道估计需要导频符号值作为先验信息的问题，提出一种基于OQAM符号特征的IAM(OCBIAM)估计算法。该算法利用IAM导频结构和OQAM实符号的有限集特征，将信道衰落系数幅度和相位分开估计，在仅获得导频位置而未知导频符号值的条件下实现了OFDM/OQAM系统半盲信道估计。并且证明了OCB-IAM算法由于利用接收符号的二阶统计量将高斯白噪声变为非随机的单音干扰，从而在中低信噪比条件下具有优于IAM算法的估计性能。仿真实验验证了理论推导的正确性和OCB-IAM算法的可靠性。

正交频分复用；偏移正交振幅调制；干扰近似法；盲信道估计；均方误差

正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术［1-3］利用各子载波之间的正交性实现了频谱效率的最大化，但需要插入循环前缀(Cyclic Prefix，CP)以对抗多径信道引起的码间串扰(Inter-Symbol Interference，ISI)［3-4］，从而降低了系统的频谱利用率。针对此问题，学者们提出了正交频分复用/偏移正交振幅调制(OFDM/Offset Quadrature Amplitude Modulation，OFDM/OQAM)技术［5-7］。该技术又被称为滤波器组多载波调制技术，可以克服传统OFDM技术在时频域上的资源浪费问题［8-9］。OFDM/OQAM技术通过设计具有良好时频特性的原型滤波器，仅在实部保证子载波之间的正交性，而将ISI与载波间干扰(Inter-Carrier Interference，ICI)集中在虚部，实现了无CP条件下无ISI，ICI的可靠传输。另外，通过合理设计原型滤波器可以保证各子载波频率响应具有更好的滚降特性，降低子载波之间的频谱泄露。由于具有上述优点，OFDM/ OQAM技术已成为IEEE802.22［9］、电力线通信［10］和认知无线电［11］等新型通信体制的备选技术标准，具有较大的研究价值。

OFDM/OQAM系统仅在实部保持正交的特性导致了各子载波信道估计的困难性，训练序列符号位置的虚部干扰将会严重影响估计性能。针对此问题，学者们提出了基于辅助训练符号的设计方案［12-13］、基于双训练符号的估计方法［14］与干扰近似法(Interference Approximate Method，IAM)［14-17］。相比之前两种算法，IAM算法具有更好的估计性能［14］，从而引起了学者的广泛关注。然而，上述三种方法或者要求发送端对训练序列进行设计，或者要求接收端知晓如训练序列符号值等发送端先验信息，因此不适用于如非合作通信等先验信息较少的环境。文献［18］提出一种基于OQAM符号协方差矩阵特征值分解的OFDM/OQAM系统半盲信道估计算法。该算法利用的是OQAM符号的统计特性，在接收样本符号个数较少时，协方差矩阵的估计误差会严重影响估计算法性能。另外，由于存在协方差矩阵估计和特征值分解等运算，因而算法的复杂度较高。

本文在分析IAM导频特征的基础上，提出一种基于OQAM符号特征的IAM(OQAM Characteristic Based-IAM，OCB-IAM)半盲信道估计算法。

1 OFDM/OQAM系统模型

1.1 OFDM/OQAM发送信号

OFDM/OQAM系统发送信号的等效基带连续时间模型为:

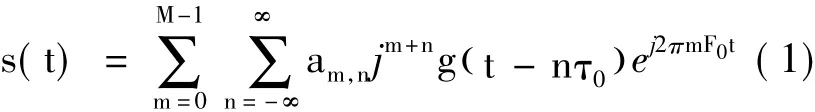
其中，j为虚数单位，m为频率序号，n为时间序号，M为子载波个数，F0为子载波间隔，τ0为OQAM符号周期，g(·)为原型滤波器冲激响应函数，am，n为时频点(m，n)上传输的实信息符号，称为一个OQAM符号。一个QAM符号的实部和虚部分别放在相邻的两个时频点上进行传输，这就是OQAM调制。设T0为复QAM符号周期，为保证相邻多载波符号之间没有重叠，须满足F0= 1/T0=1/(2τ0)。相比于传统OFDM系统以周期T0传输一个复QAM符号，OFDM/OQAM系统以周期τ0传输实OQAM符号，两者频谱效率相同。

相比传统OFDM系统模型，OFDM/OQAM系统模型中引入原型滤波器分量，通过合适控制原型滤波器参数使各子载波具有更好的频域特性，可以降低传统OFDM子载波在频域上sinc函数形式所带来的频谱旁瓣泄露。

设原型滤波器函数的频率偏移函数:

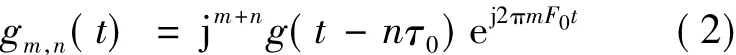
满足:

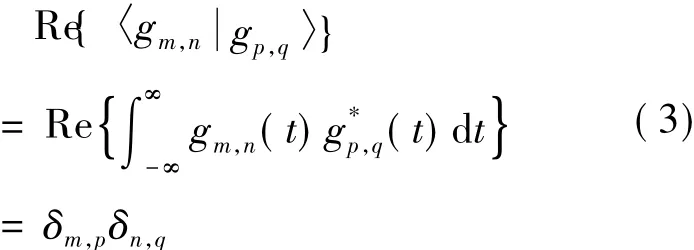
其中，Re{·}代表取实部。当且仅当m=p时，δm，p=1。若(m，n)≠(p，q)，则:

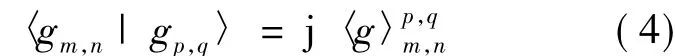
其中，〈g〉pm，，q

n为纯实数。从式(4)中可以看出，在不同时频点上，原型滤波器偏移函数在实部保持正交，因此利用仅在实部传输符号的OQAM调制方案，将不会产生ISI和ICI。相比于传统OFDM系统，节省了传输CP所需的带宽资源。

设计具有较好时频特性的原型滤波器可以保证上述正交性，在不失一般性的前提下，采用PHYDYAS项目中所采用的滤波器参数［11］，其原型滤波器频域参数见表1。

表1 PHYDYAS项目中原型滤波器频域参数Tab.1 Filter frequency coefficients in PHYDYAS project

其中，K为滤波器频域重叠系数，滤波器频域长度为2K-1，频域系数为［G3G2G1G0G1G2G3］。滤波器时域长度L=MK，时域冲激响应函数为:

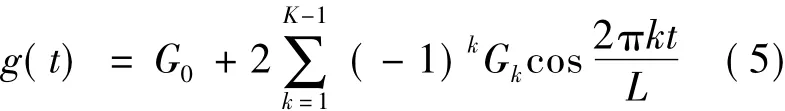
1.2 OFDM/OQAM信道估计问题

在多径衰落信道下，文献［14］中证明时频点(m0，n0)上接收符号为:

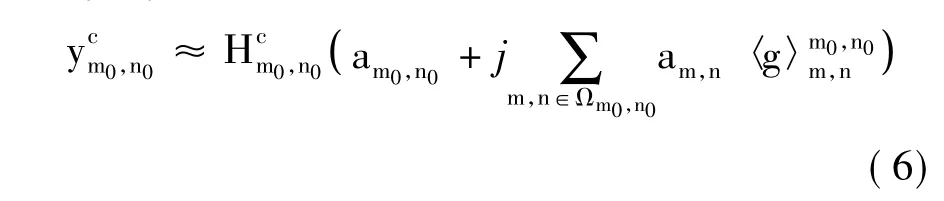
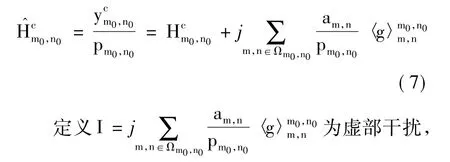
由于原型滤波器冲激响应函数为实函数，从式(1)中jm+n分量可以看出，在不同时频点，符号是实虚相间分布的，为了与PHYDYAS项目中参数相对应，同时更便于描述IAM算法，时频点(m0，n0)接收符号重新定义为:

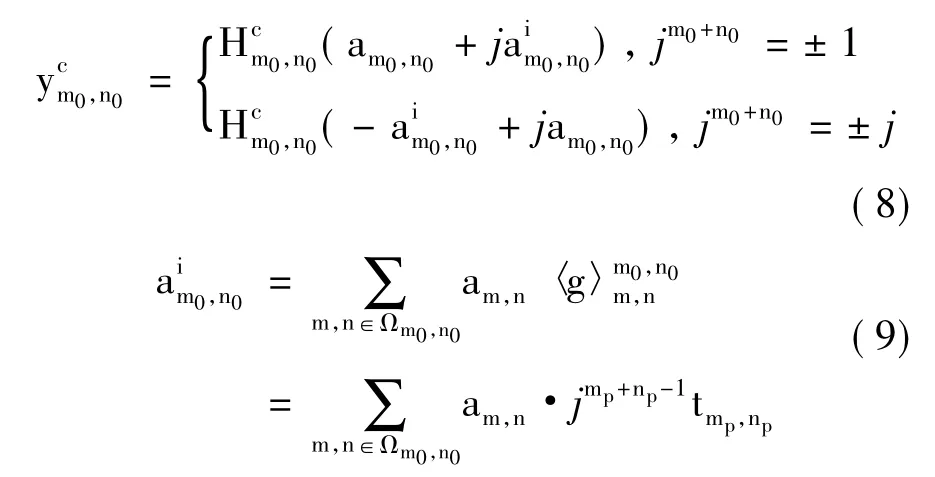
其中，mp=m-m0，np=n-p为原型滤波器虚部干扰响应，其值与原型滤波器系数有关。PHYDYAS项目中原型滤波器虚部干扰响应见表2。可以看出〈=对任意(mp，np)均为实数，可保证原型滤波器的实部正交性。

2 IAM算法

2.1 传统IAM算法

IAM算法是目前OFDM/OQAM系统中性能最好的信道估计方法［14］，其导频结构如图1所示。从图1中可以看出，导频符号为实OQAM符号，数值为±p，导频符号前后时隙符号置为0，以保证导频符号位置的虚部干扰仅来自于相邻子载波上的导频符号。图1中的导频符号是每两个正负相间分布的，目的是为了与原型滤波器中jm+n分量相对应，若p'=p或p'=-p，则p·jm+n=p'。

图1 IAM算法导频结构Fig.1 Preamble framework of IAM algorithm

设导频符号时域位置n=0，由于导频符号前后时隙符号为0，因此根据原型滤波器干扰系数容易计算jm0+n0=±1时导频符号位置的接收符号:

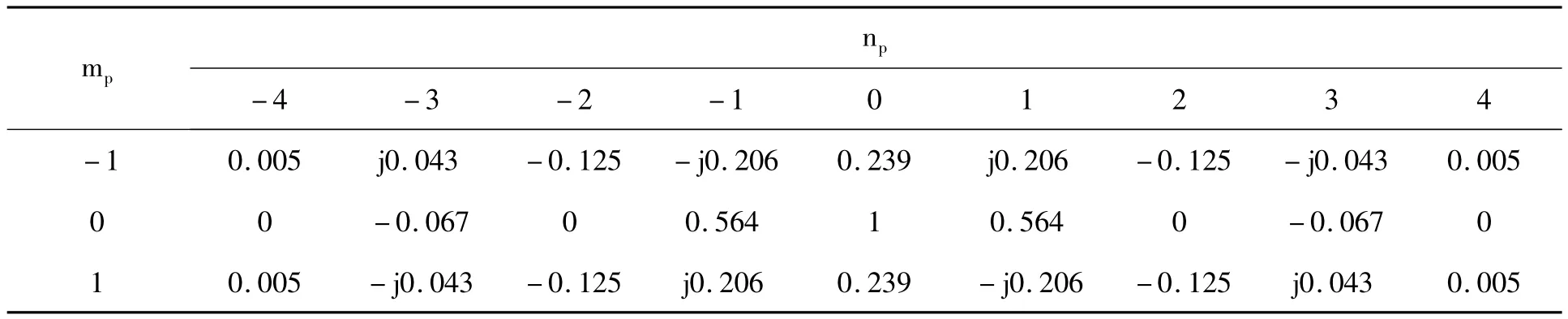
表2 干扰响应Tab.2 Impulse response

2.2 OCB-IAM算法

利用IAM算法进行OFDM/OQAM信道估计需要导频符号p的值作为先验信息，因此不适用于非合作通信等先验信息较少的条件。针对此问题，提出一种基于OQAM符号特征的IAM估计算法，该算法不需要利用p值，在仅获得导频位置的条件下，实现OFDM/OQAM信道估计。OCB-IAM算法将衰落系数的相位和幅度分开估计，设:

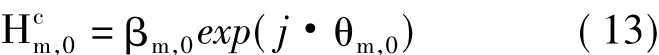
其中，βm，0为衰落系数的幅度，θm，0为衰落系数的相位。定义函数φ(·)为求相位。

首先估计θm，0。由于导频符号p为实数，容易得到θm，0的估计值:

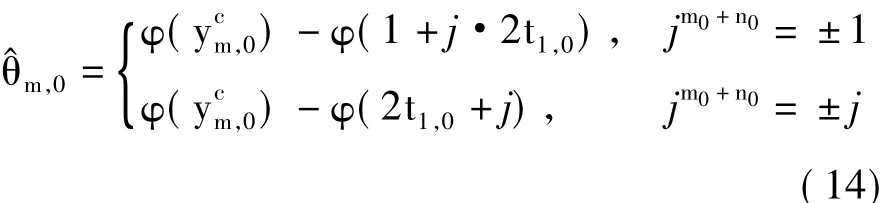
然后估计βm，0。对于子载波m上的信息符号am，n，根据式(8)定义:

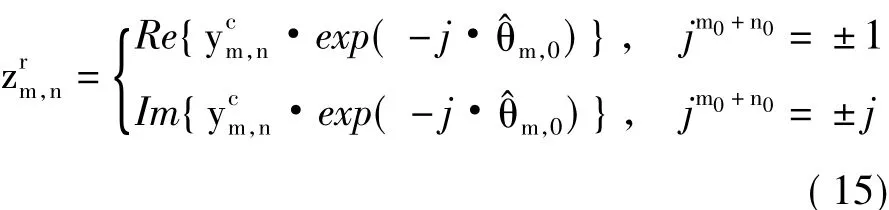
其中，Im{·}代表取虚部，上标r代表该变量为实数。消除接收符号中衰落系数的相位影响，则可得:

其中，am，n为OQAM符号。定义OQAM符号集A= {α1，α2，…，αS}，则可得OQAM符号的平均能量:

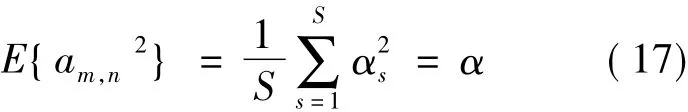
其中，E{·}表示求期望，则可得:

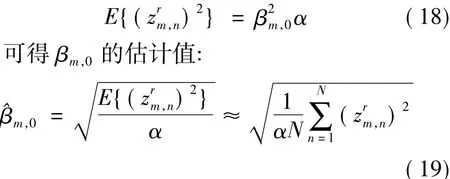
利用式(14)估计衰落系数相位θm，0时，默认p＞0，若p＜0，则估计值与真值之间存在180°的相位旋转，这就是盲信道估计的相位模糊问题，因此OCB-IAM算法要求导频符号p＞0。可以看出，对于IAM算法，导频符号正负对性能没有影响，为方便起见都会设其大于0，因此该条件一般情况下可以保证。

3 估计性能理论分析

本节从理论角度分析IAM算法和OCB-IAM算法的估计性能。考虑到式(10)和式(11)形式相同，仅以式(10)为例，在含噪情况下，式(10)可重写为:

下面分析OCB-IAM算法的估计性能，考虑到OCB-IAM算法将衰落系数的幅度和相位分开估计，因此分别分析幅度和相位的估计性能。容易得衰落系数的相位估计信噪比与IAM算法相同:

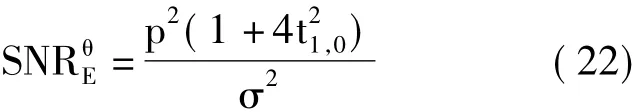
含噪条件下，式(16)可重写为:

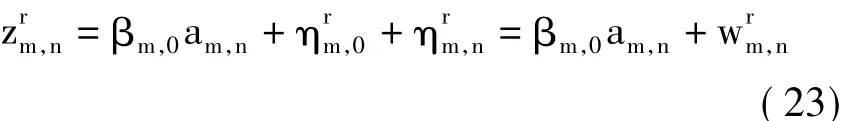
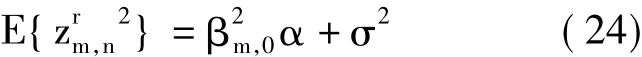
从式(24)可以看出，OCB-IAM算法求均方值的过程将方差为σ2的高斯白噪声转变为值为σ2的固定单音干扰。在此基础上可引出定理1。

定理1在信噪比与信干比相同条件下，含单音干扰的OCB-IAM估计算法均方误差小于含高斯白噪声的IAM估计算法。证明:定义两估计式:

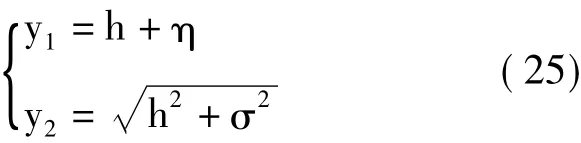
其中，h为信道衰落系数，η为零均值方差为σ2的高斯白噪声，为固定单音干扰，此时信噪比与信干比相同=y1为含高斯白噪声条件下h的估计值=y2为含单音干扰条件下h的估计值。可得两估计式的均方误差分别为:

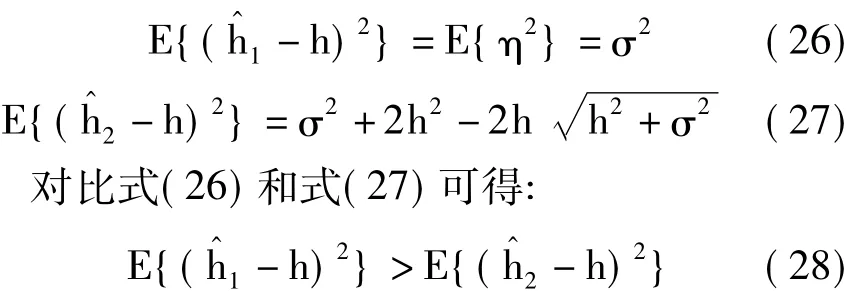
定理1证毕。

式(28)默认接收符号均方值可以精确获得，是一种理论极限情况。达到极限的条件是式(19)利用的信息符号无限多，N珋∞，即:

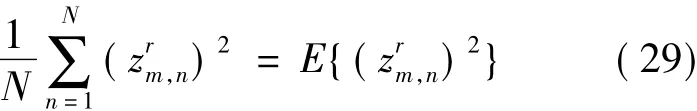
实际应用中，N越大，越接近理论极限。在中低信噪比条件下，σ2较大，式(26)与式(27)之差也就较大，OCB-IAM算法由定理1获得的性能改善影响将会大于均方值估计误差的影响和导频符号值不确定性的影响，因此OCB-IAM算法的估计性能优于IAM算法的。

4 数值仿真与结果分析

分别仿真利用文献［18］提出的算法、IAM算法与OCB-IAM算法进行OFDM/OQAM信道估计的均方误差性能和误比特率(Bit-Error Ratio，BER)性能，仿真条件见表3。其中信道采用IEEE802.22标准中的信道模型［14］。

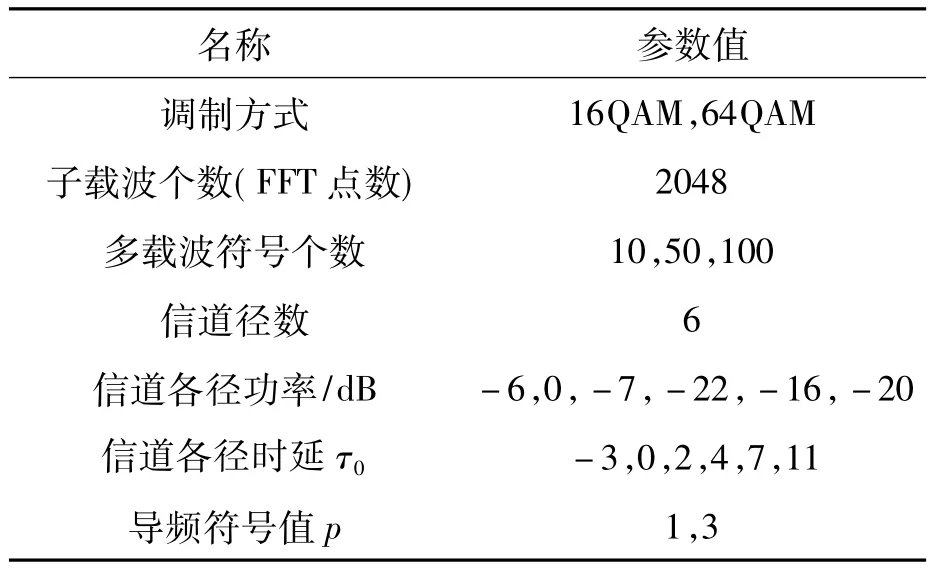
表3 仿真参数Tab.3 Simulation parameters

仿真中不同导频符号值p所要体现的是发送端不同导频符号值对估计算法性能的影响，OCBIAM算法本身不利用p值信息。

估计算法的均方误差性能利用蒙特卡洛仿真分析，设第l次仿真中第m个子信道衰落系数真值为估计值为，仿真次数NM=100，则均方误差值:

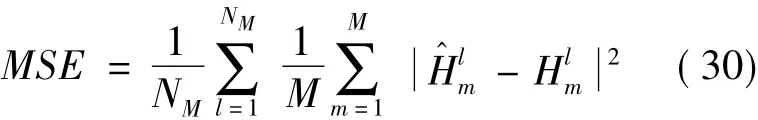
在均方误差性能仿真中，信道各径衰落将服从CN(0，1)的复高斯分布，以保证蒙特卡洛仿真的统计性。

图2为不同导频符号值p条件下文献［18］的算法、IAM算法与OCB-IAM算法MSE性能对比。仿真中设调制方式为16QAM，多载波符号个数N=100。从图2中可以看出，在高信噪比条件下，文献［18］所提出的算法具有较高的MSE平层，IAM和OCB-IAM算法估计性能明显优于文献［18］所提出的算法的。在中低信噪比条件下，IAM与OCB-IAM算法p=3时的MSE性能优于p=1时9.5dB(10lg(32/12)=9.5dB)，并且OCBIAM算法的性能均优于IAM算法的，验证了估计性能理论分析的正确性。在高信噪比条件下，IAM算法的均方误差仍随信噪比的增加线性下降。而OCB-IAM算法则遇到MSE平层，原因是此时定理1获得的性能改善影响将会小于均方值估计误差和导频符号值不确定性引起的不利影响，导致OCB-IAM算法性能无法再提升。

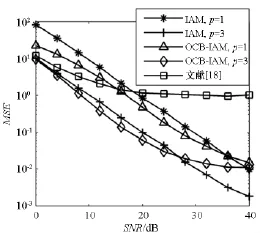
图2 不同p值条件下三种算法MSE性能对比Fig.2 MSE comparing of three algorithm with different p

设调制方式为16QAM，p=3，图3为不同多载波符号个数N条件下OCB-IAM算法MSE性能对比。从图3中可以看出，OCB-IAM算法在接收样本符号个数较少时仍能表现出良好的估计性能。中低信噪比条件下不同N时OCB-IAM算法估计性能基本相同，此时MSE曲线属于下降区域。高信噪比条件下N越大，估计性能越好，此时MSE曲线属于平层区域。因此在中低信噪比条件下可以利用较少的符号以提高算法效率，高信噪比条件下可以利用较多符号以提升估计性能。

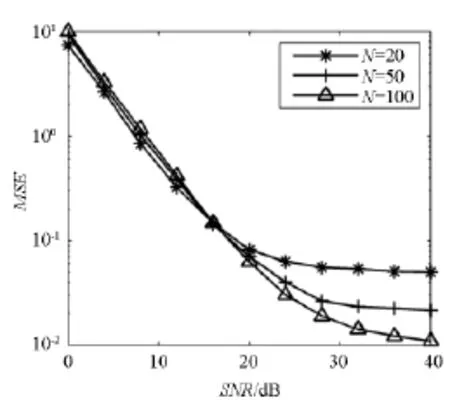
图3 不同N值条件下OCB-IAM算法MSE性能对比Fig.3 MSE comparing of OCB-IAM algorithm with different N

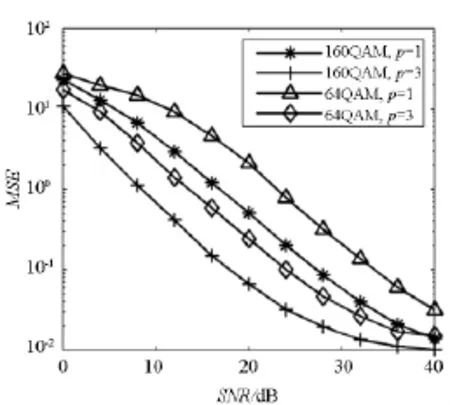
图4 不同p值、不同调制方式条件下OCB-IAM算法MSE性能对比Fig.4 MSE comparing of OCB-IAM algorithm with different p and differentmodulation mode

设多载波符号个数N=100，图4为不同调制方式和p值条件下OCB-IAM算法MSE性能对比。从图4中可以看出，16QAM调制方式时OCB-IAM算法性能优于64QAM调制时的。原因是16QAM调制时α=5；64QAM调制时α=(1+ 9+25+49)×2/8=21。可以看出两种调制方式下信噪比相同则衰落系数幅度估计性能相同。由于16QAM调制具有较小的α，因此具有较小的噪声功率σ2，此时衰落系数相位估计信噪比16QAM优于64QAM 6.2dB(10lg(21/5)=6.2dB)。

图5为不同导频符号值条件下文献［18］的算法、IAM算法与OCB-IAM算法BER性能对比。可以看出三种算法BER性能对比结果与MSE性能对比结果相同，原因不多做赘述。

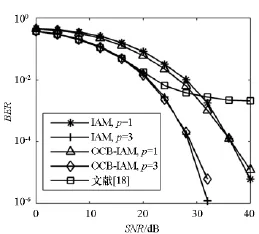
图5 不同p值条件下三种算法BER性能对比Fig.5 BER comparing of three algorithm with different p

5 结论

由于接收位置的被动性，非合作通信接收端所能够利用的先验信息比合作接收端少，并且往往具有更低的接收信噪比，因此先验信息较少且信噪比较低条件下OFDM/OQAM系统信道估计技术研究是一项很有意义的工作。在IAM导频结构的基础上，提出一种基于OQAM实符号有限集特征的OFDM/OQAM系统半盲信道估计算法。仿真实验验证了上述结论的正确性与OCB-IAM算法的可靠性。并且算法复杂度较低，易于实现。

References)

［1］Strohmer T，Beaver S.Optimal OFDM design for timefrequency dispersive channels［J］.IEEE Transactions on Communications，2003，51(7):1111-1122.

［2］王丽洁，唐艺，黄勤飞，等.协同OFDM放大前传空时编码系统中的功率分配［J］.国防科技大学学报，2012，34(3):142-147.WANG Lijie，TANG Yi，HUANG Qinfei，et al.The power allocation of cooperative OFDM-based amplify-and-forward STBC system［J］.Journal of National University of Defense Technology，2012，34(3):142-147.(in Chinese)

［3］李颖，魏急波.OFDM抗多径机理分析与系统仿真［J］.国防科技大学学报，2004，26(5):34-38.LIYing，WEIJibo.Analysis and simulation of the principle of antimultipath in the OFDM system［J］.Journal of National University of Defense Technology，2004，26(5):34-38.(in Chinese)

［4］Katselis D，Kofidis E，Rontogiannis A，etal.Preamble-based channel estimation for CP-OFDM and OFDM/OQAM systems: a comparative study［J］.IEEE Transactions on Signal Processing，2010，58(5):2911-2916.

［5］Le Floch B，Alard M，Berrou C.Coded orthogonal frequency division multiplex［J］//Proceedings of the IEEE，1995，83(6):982-996.

［6］Bölcskei H，Duhamel P，H leiss R.Orthogonalization of OFDM/OQAM pulse shaping filters using the discrete Zak transform［J］.Signal Processing，2003，83(7):1379-1391.

［7］Siohan P，Siclet C，Lacaille N.Analysis and design of OFDM/ OQAM systems based on filterbank theory［J］.IEEE Transactions on Signal Processing，2002，50(5):1170-1183.

［8］Farhang-Boroujeny B.OFDM versus filter bank multicarrier: development of broadband communication systems［J］.IEEE Signal Processing Magazine，2011，28(3):92-112.

［9］Schaich F.Filterbank based multi carrier transmission (FBMC)-evolving OFDM:FBMC in the context of WiMAX［C］//Proceedings of European Wireless Conference，2010(4):1051-1058.

［10］Lin H，Siohan P.Capacity analysis for indoor PLC using different multi-carrier modulation schemes［J］.IEEE Transactions on Power Delivery，2010，25(1):113-124.

［11］Viholainen A，Bellanger M，Huchard M.WP5:prototype filter and filter bank structure［R］.PHYDYAS Deliverable D5.1，ICT-211887，2009.

［12］Javaudin J P，Lacroix D，Rouxel A.Pilot-aided channel estimation for OFDM/OQAM［C］//Proceedings of IEEE VTC，2003(3):1581-1585.

［13］He X J，Zhao Z F，Zhang H G.A pilot-aided channel estimation method for FBMC/OQAM communications system［C］//Proceedings of IEEE ISCIT，2012:175-180.

［14］LéléC，Javaudin JP，Legouable R，et al.Channel estimation methods for preamble-based OFDM/OQAM modulations［J］.European Transactions on Telecommunications，2008，19(7): 741-750.

［15］Du JF，Signell S.Novel preamble-based channel estimation for OFDM/OQAM systems［C］//Proceedings of IEEE ICC，2009:1-6.

［16］Kofidis E，Katselis D，Rontogiannis A，et al.Preamblebased channe lestimation in OFDM/OQAM systems A review［J］.Signal Processing，2013，93(7):2038-2054.

［17］程国兵，肖丽霞，肖悦，等.一种改进的OFDM/OQAM系统信道估计算法［J］.电子与信息学报，2012，34(2): 427-432.CHENG Guobing，XIAO Lixia，XIAO Yue，et al.An improved channel estimation algorithm for OFDM/OQAM systems［J］.Journalof Electronics＆Information Technology，2012，34(2):427-432.(in Chinese)

［18］Hou W K，Champagne B.Semi-blind channel estimation for OFDM/OQAM systems［J］.IEEE Signal Processing Letters，2015，22(4):400-403.

Sem i-blind channel estimation for OFDM/OQAM system

LIXiaotian1，2，LEI Jing2，LIUWei2，CAOWei2，LIYanbin1
(1.The 54th Research Institute，China Electronics Technology Group Corporation，Shijiazhuang 050081，China；2.College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China)

Interference approximate method(IAM)for orthogonal frequency division multiplexing/offset quadrature amplitude modulation (OFDM/OQAM)channel estimation needs the value of preamble at the background of un-cooperative communications.Motivated by this consideration，an OQAM characteristic based-IAM(OCB-IAM)algorithm，which used IAM preamble framework and OQAM symbols’real finitealphabet characteristics，was introduced.OCB-IAM algorithm estimated the amplitude and phase of channel fading coefficients separately，and just needed preamble position，which was a kind of semi-blind channel estimators.OCB-IAM algorithm converted white Gaussian noise into single tone interference based on the second-order statistics of

symbols.Then it could be proved that OCB-IAM algorithm has a better performance than IAM algorithm in medium and low SNR regime.Numerical results show the validity of theoretical analysis and the reliability of OCB-IAM algorithm.

orthogonal frequency division multiplexing；offset quadrature amplitude modulation；interference approximate method；blind channel estimation；mean square error

TN911

A

1001-2486(2015)05-169-06

10.11887/j.cn.201505026

http://journal.nudt.edu.cn

2015-01-14

国家自然科学基金资助项目(61372098，61101074)

李啸天(1986—)，男，河北石家庄人，博士研究生，E-mail:lxtrichard@126.com；雷菁(通信作者)，女，教授，博士，硕士生导师，E-mail:leijing@nudt.edu.cn