机载雷达空时二维海杂波分析

熊昭华,欧阳缮

机载雷达空时二维海杂波分析

熊昭华,欧阳缮

(桂林电子科技大学信息与通信学院,广西桂林 541004)

为了给机载雷达海杂波的STAP处理提供自由度信息和功率分布信息,以脉冲多普勒相控阵雷达为基础,分析了正侧阵、斜面阵和前向阵3种阵面下机载雷达空时二维海杂波的分布特性,提出了一种K分布海杂波生成方法,实现了3种阵面下海杂波特征谱和功率谱的仿真。仿真结果表明,机载雷达空时二维海杂波的自由度比地杂波大0.6~2.5倍,因此,海杂波滤波器的阶数需增大相同倍数;同时,海杂波功率谱波脊比地杂波宽很多,设计滤波器的频域响应时要作相应调整。

机载雷达;3种阵面;海杂波;特征谱;功率谱

环境杂波的存在,让雷达综合能力的发挥面临严峻考验。机载脉冲多普勒(pulse doppler,简称PD)相控阵雷达主要工作在下视状态,会受到严重的杂波干扰,滤波器能否消除杂波,对雷达的性能影响很大,尤其是严峻的海杂波干扰,对目标检测的影响更不可小觑[1]。机载雷达与散射单元的相对运动,不仅平移了主瓣杂波,还改变了其他方位的杂波的多普勒频率,使整个杂波谱被展宽,造成目标信号被淹没的概率明显升高。

1973年Brennan提出空域时域二维处理思想,将滤波技术从单一空域提高到了空域时域二维的高度。文献[2]研究了空时二维杂波谱的分布,揭示了空时自适应处理(space time adaptive processing,简称STAP)在环境杂波抑制上的巨大优势。对杂波进行STAP处理时,滤波器阶数与杂波自由度正相关,频域响应与杂波功率分布逆相关。因此,若要对机载雷达空时二维海杂波进行STAP处理,应掌握特征谱和功率谱的分布特性,以提供自由度信息和功率分布信息。

机载雷达空时二维地杂波散射单元的回波是独立同分布的随机序列,在正侧阵、斜面阵和前向阵形式下,特征谱有较快的收敛特性,且功率谱依次呈现直线、半椭圆和半圆的分布特性。

在海洋环境中,散射单元不断运动,不同脉冲间的回波具有时间、空间相关性,因此,机载雷达海杂波不同于地杂波,其特征谱和功率谱分布特性会更复杂。目前对机载雷达海杂波特征谱和功率谱分布特性的研究尚未见诸报道。鉴于此,通过分析机载雷达空时二维海杂波的分布特性,提出一种机载K分布海杂波生成方法,实现了3种阵面下机载雷达空时二维海杂波特征谱和功率谱的仿真。

1 机载雷达空时二维海杂波分布

机载雷达系统各关联量的几何关系如图1。设阵元数为N,雷达阵面偏置角为θp,平台速度为V,高度为H,海面散射单元的轴向方位角、方位角和俯仰角分别为θa、θ和φ,空间锥角为Ψ,根据多普勒频率的定义,海面回波的多普勒频率fd等于平台运动引起的多普勒频率与自身运动引起的多普勒频率的叠加[3],故该散射单元回波的fd为:

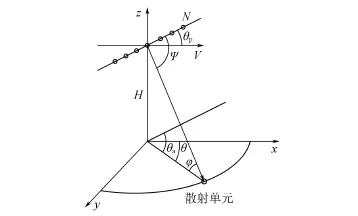
图1 机载雷达系统各关联量的几何关系Fig.1 The geometry diagram of airborne radar system

其中:λ为载波波长;νsea为回波的径向速度,是与风速相关的符合(0,1)均匀分布的随机数。式(1)可改写为:

其中fd,max=2V/λ,表示vsea=0时的fd。

在雷达信号的STAP处理中,对空域、时域分别进行滤波,通过调整各自滤波域的权值来增强或减弱其多普勒响应(对应时域)或空间锥角余弦(对应空域)响应的特性。因此,式(2)可改为:

其中:fr为脉冲重复频率。根据θp的取值不同,机载雷达空时二维海杂波可分3种情况:

1)正侧阵情形。θp=0,阵面与飞行方向V一致,式(3)为:

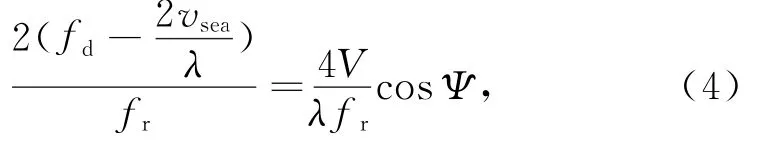
可改写为:

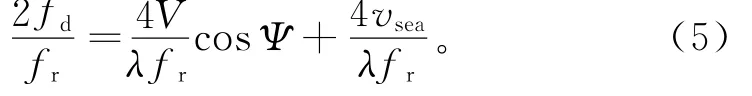
由式(5)可知,2fd/fr与cosΨ为线性关系,海杂波谱的波脊应为直线。

2)斜面阵情形。θp≠0,θp≠π/2,且φ为常数,式(3)为椭圆方程,海杂波谱的波脊为椭圆形。

3)前向阵情形。θp=π/2,式(3)可改写为:

式(6)为圆方程,海杂波谱的波脊为圆形。

2 机载雷达空时二维海杂波建模及其特征谱、功率谱

实际的天线都是M×N平面阵,阵元间距d,主瓣指向(θ0,φ0),主瓣锥角Ψ0,且有关系式cosΨ=

cosθcosφ,令n=1,2,…,N,m=1,2,…,M,In、Im是阵元的加权系数,平面阵天线的方向图为:

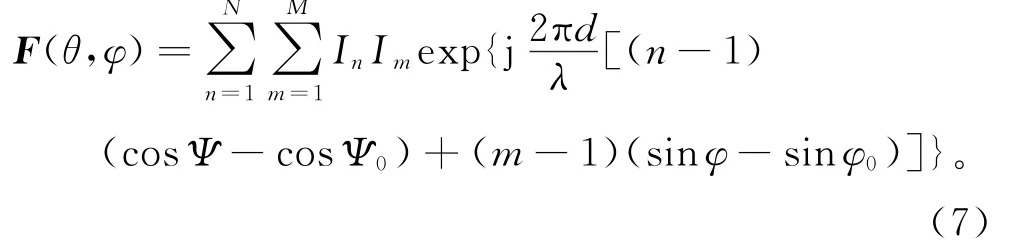
若独立控制平面阵的每个阵元,则系统需要处理的自由度太大,现有机载计算机无法实时处理。通常做法是聚合各列阵元的微波信号,将其等效为线阵[4-5],再对线阵进行控制,可大大降低其难度。

假设总采样信号由海杂波与噪声叠加而成,采样模型应满足[6]:

1)载机H、V不变;

2)在信号处理的一个时间间隔内,主瓣指向近似不变;

3)不同脉冲时刻,同一个散射单元的海杂波是时间相关且均值为Chi序列的瑞利分布序列。

令cl(n,k)表示第n个阵元、k个脉冲、l个距离环的机载雷达空时二维海杂波的采样数据,其表达式为:

其中:k=1,2,…,K,K为总脉冲数目;l=1,2,…,L, L为总距离环数;F(θ,φl)为发射和接收方向图;Rl为第l个距离环的径向距离;φl为第l个距离环的俯仰角;Ac(θ,φl)为散射单元的面积;y(θ,φl,k)为K分布海杂波的随机幅度;B(θ,φl,k)为海杂波随机相位,符合(0,2π)均匀分布;ωs(θ,φl)为空域角频率,

ωt(θ,φl)为时域角频率,

散射单元海杂波的随机幅度y的概率密度函数[7]为:

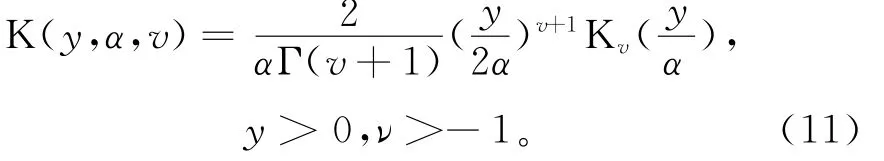
其中:K(·)为K分布函数;v为形状参数;α为尺度参数;Kv(·)为v阶修正的柱贝塞尔函数;Γ(v+1)为v+1阶伽马函数。

SIRP法把K分布海杂波的幅度等价为2个不相关的分量之积,可写为y=xs。其中:x为时间相关的瑞利分量;s为空间相关的Chi分布分量。利用SIRP法生成机载雷达海杂波序列y的流程框图如图2所示。图中:Nθ为方位单元数目;y(Nθ,L,K)为y(θ,φl,k)的集合;g(Nθ,L,K)为复高斯白噪声; c(Nθ,L)为与g(Nθ,L,K)相互独立的Chi分布序列; H1(z)为线性滤波器,其特性由海杂波的x(Nθ,L,K)的时间相关性决定,它使输出的x(Nθ,L,K)具有所要求的高斯型功率谱。由于相关函数与功率谱呈傅里叶变换对的关系,可用傅里叶级数的展开求H1(z)的各阶系数。H1(z)各阶时域系数为:

图2 SIRP法生成机载雷达海杂波序列y的框图Fig.2 The block diagram of generating sequence y based on SIRP method

其中:σf为海杂波功率谱密度的3 dB带宽;n1为滤波器阶数;Ts为采样间隔(等于fr的倒数)。g(Nθ,L,K)经过H1(z)得到x(Nθ,L,K),

线性滤波器H2(z)使输出的调制分量s(Nθ,L)具有指数衰减[8]的空间相关性。空间相关性通过下式实现:

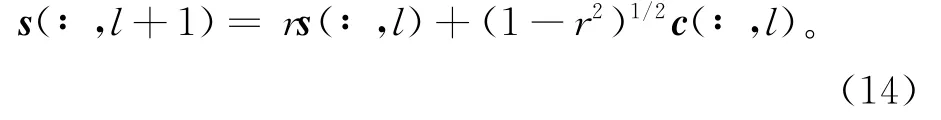
空间相关函数r为:

其中:R为雷达距离分辨率;p为相关距离。

单个距离环N路K个脉冲的cl(n,k)可用NK×1维的列矩阵表示:

其中cl(n)=[cl(n,1),cl(n,2),…,cl(n,K)]T。

假设只存在海杂波、噪声,总采样信号的相关协方差矩阵为:

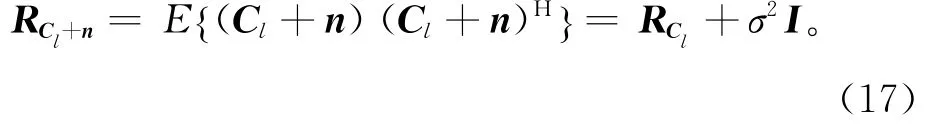
其中:n为噪声矢量;I为NK×NK的单位矩阵。式(18)的AML估计为:

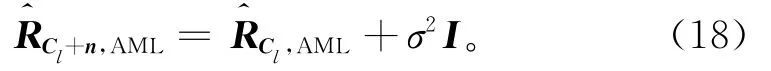
采用最大渐进似然(approximated maximum likelihood,简称AML)法估计RCl,选取的距离环数目为2NK,

其中0≤i≤2,且R^Cl,AML(0)=RCl,NSCM。RCl,NSCM为距离环的机载雷达海杂波的正则化协方差矩阵(normalized sample covariance matrix,简称NSCM)[9],

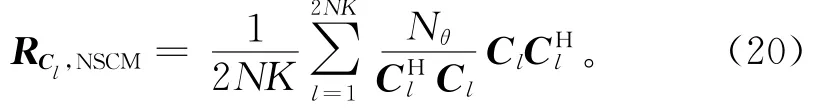
由于海杂波与噪声为相关协方差矩阵正定,对此进行谱分解处理可得其所有特征值,

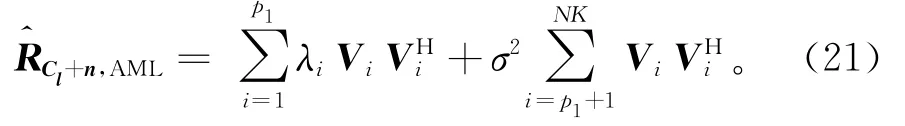
其中:Vi为第i个特征矢量;λi为的p1个正实数特征值;其余NK-p1个值近似等于噪声方差σ2,若杂噪比为60 dB,则其值等于海杂波相关协方差矩阵最大值的10-6。将NK个特征值作降序排列,可得机载雷达空时二维海杂波的特征谱,其自由度为其中较大值的个数p1。

定义空、时域导向矢量:

那么二维空时导向矢量S为:

其中⊗为Kronecker积。采用最小方差谱[10](也称似然谱)分析机载雷达空时二维海杂波,似然谱的数学描述为:

3 特征谱、功率谱的Matlab仿真

假设在2级海情下,天线是8行8列的平面阵,雷达距离分辨率ΔR为15 m,相关距离p=6.5 m。在Matlab平台上仿真参数设置:正侧阵θp=0°,斜面阵θp=30°,前向阵θp=90°,H=6000 m,V=120 m/s,Nθ=180,λ=0.32 m,fr=1500 Hz,K=10,v=1.5,α= 1,σf=20 Hz,vsea=4.5U(0,1),U(0,1)为符合(0,1)均匀分布的随机数。为了直观地看到机载雷达海杂波与地杂波在特征谱、功率谱上的区别,仿真中加入了地杂波的模拟结果。

3.1 正侧阵雷达空时二维海杂波与地杂波的比较

机载正侧阵雷达空时二维地杂波的自由度为N+ K-1[11]。本仿真中,阵元数N=8,脉冲采样数K= 10,则N+K-1=17。图3为机载正侧阵雷达空时二维杂波特征谱模拟结果。从图3可看出,对于机载正侧阵雷达空时二维海杂波,自由度增加很多,已达60,远远大于地杂波17的自由度,两者差距2.5倍。

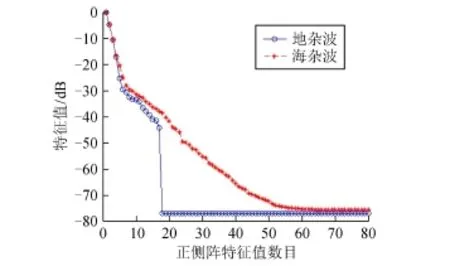
图3 机载正侧阵雷达空时二维杂波特征谱模拟结果Fig.3 The eigenspectrum simulation of airborne radar spatial-temporal clutter in sidelooking array

图4 为机载正侧阵雷达空时二维杂波功率谱模拟结果。从图4可看出,机载正侧阵雷达空时二维地杂波的功率谱波脊呈刀背状,即2fd/fr与cosΨ为线性关系[5]。对于机载正侧阵雷达空时二维海杂波,根据式(5)可知,2fd/fr与cosΨ近似呈线性关系,即海杂波的功率谱呈刀背状的波脊。此外,海杂波波脊比地杂波波脊有一定程度的展宽,展宽对STAP处理中滤波器的频域响应设计有很大的影响。因为滤波器的频域响应与杂波功率谱波脊逆相关,所以设计频域响应时,如果未考虑波脊的展宽,就无法滤除海杂波,造成后续检测虚警。

图4 机载正侧阵雷达空时二维杂波功率谱模拟结果Fig.4 The power spectrum simulation of airborne radar spatial-temporal clutter in sidelooking array

3.2 斜面阵雷达空时二维海杂波与地杂波的比较

图5为机载斜面阵雷达空时二维杂波特征谱模拟结果。从图5可看出,对于斜面阵,机载雷达空时二维地杂波自由度为27,比正侧阵有明显的增加。对于机载斜面阵雷达空时二维海杂波,自由度增加很多,自由度已达64,远大于机载斜面阵雷达空时二维地杂波自由度27,两者差距为1.4倍。

图6为机载斜面阵雷达空时二维杂波功率谱模拟结果。从图6可看出,地杂波的功率谱中,2fd/fr与cosΨ不再呈现线性关系,波脊为椭圆弧线状。海杂波功率谱中,2fd/fr与cosΨ也是弧线关系,波脊呈半椭圆状。此外,海杂波波脊比地杂波波脊有明显的展宽,该展宽对海杂波滤波器的频域响应设计同样有影响,STAP处理时应予以考虑。

图5 机载斜面阵雷达空时二维杂波特征谱模拟结果Fig.5 The eigenspectrum simulation of airborne radar spatial-temporal clutter in slant-side looking array

图6 机载斜面阵雷达空时二维杂波功率谱模拟结果Fig.6 The power spectrum simulation of airborne radar spatial-temporal clutter in slant-side looking array

3.3 前向阵雷达空时二维海杂波与地杂波的比较

图7为机载前向阵雷达空时二维杂波特征谱模拟结果。从图7可看出,地杂波的自由度为32,海杂波的自由度增加较多(自由度为50),两者差距为0.6倍,比正侧阵2.5倍、斜面阵1.4倍有较大幅度的减小。

图8为机载前向阵雷达空时二维杂波功率谱模拟结果。从图8可看出,地杂波的功率谱2fd/fr与cosΨ不再呈线性关系,波脊为半圆弧线状。海杂波的功率谱2fd/fr与cosΨ也是弧线关系,波脊呈半圆状。此外,海杂波波脊比地杂波波脊有明显的展宽,尤其是波脊背部,展宽更明显,该展宽对海杂波滤波器的频域响应设计有很大影响,空时自适应处理时应予以考虑。

图7 机载前向阵雷达空时二维杂波特征谱模拟结果Fig.7 The eigenspectrum simulation of airborne radar spatial-temporal clutter in forward looking array

图8 机载前向阵雷达空时二维杂波功率谱模拟结果Fig.8 The power spectrum simulation of airborne radar spatial-temporal clutter in forward looking array

4 结束语

以脉冲多普勒相控阵雷达为平台,分析了正侧阵、斜面阵、前向阵下机载雷达空时二维海杂波的分布特性,仿真得到了3种特征谱和功率谱。仿真结果表明,相同阵面下,机载雷达空时二维海杂波的自由度比机载雷达地杂波的自由度大得多,差距分别为0.6、1.4、2.5倍。因此,在设计机载雷达空时二维海杂波滤波器的阶数时,应增大其阶数;机载雷达空时二维海杂波的功率谱波脊比机载雷达地杂波的功率谱波脊展宽得更多,在设计频域响应时要作相应调整,这有利于抑制机载雷达海杂波,提高目标检测能力。

[1] 阮锋,李明,吴顺君.一种简捷的机载PD雷达地杂波仿真方法[J].现代雷达,2006,28(12):30-32.

[2] 夏德平.空时二维自适应处理技术应用研究[D].南京:南京理工大学,2008:8-15.

[3] 伍勇.空时自适应杂波抑制[D].北京:清华大学,2008: 12-20.

[4] 王永良.空时自适应信号处理[M].北京:清华大学出版社,2000:133-138.

[5] 郑辉.机载雷达杂波建模技术研究[D].成都:电子科技大学,2010:22-30.

[6] 黄斌.机载雷达海杂波建模与仿真[D].西安:西安电子科技大学,2009:40-42.

[7] 周万幸.基于SIRP的时空相关K-分布海杂波仿真研究[J].电子学报,2009,37(12):2672-2676.

[8] 赵海云,胡学成.时空二维相关K分布雷达海杂波建模与仿真[J].中国电子科学研究院学报,2008,3(5):515-519.

[9] 谢洪森,邹鲲,杨春英,等.海杂波协方差矩阵估计及其对目标检测性能的影响[J].系统工程与电子技术, 2011,33(10):2174-2178.

[10] 娄军,陆必应,周智敏.机载相控阵雷达杂波抑制仿真研究[J].系统仿真技术及其应用,2008,10:564-568.

[11] 陈晓初.机载雷达二维杂波特征谱研究[J].现代雷达, 1994,16(3):29-36.

编辑:翁史振

Analysis of spatial-temporal sea clutter for airborne radar

Xiong Zhaohua,Ouyang Shan
(School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin 541004,China)

In order to provide the freedom and power distribution information in the spatial-temporal adaptive processing for airborne radar sea clutter,the distribution characteristics of airborne phased array radar spatial-temporal sea clutter in sidelooking,slant-side looking,and forward looking cases are discussed base on pulse Doppler phased array.A generation method of K distribution sea clutter is proposed,and the three fronts of eigenspectrum and power spectrum of airborne radar sea clutter are simulated respectively.The results show that the freedom of sea clutter is 0.6-2.5 times higher than ground clutter.So the orders of the filter are increased by the same times,the wave ridge of sea clutter power spectrum is extended to ground clutter,the frequency response of filter is adjusted at the same time.

airborne radar;three fronts of arrays;sea clutter;eigenspectrum;power spectrum

TN911

A

1673-808X(2015)05-0350-06

2015-04-01

广西自然科学基金(2013GXNSFFA019004)

欧阳缮(1960-),男,江西安福人,教授,博士,研究方向为通信和雷达信号处理、自适应滤波理论和应用。E-mail:hmoysh@guet.edu.cn引文格式:熊昭华,欧阳缮.机载雷达空时二维海杂波分析[J].桂林电子科技大学学报,2015,35(5):350-355.