基于灰色模型和支持向量机的组合预测模型

刘齐林,曾 玲,曾祥艳

基于灰色模型和支持向量机的组合预测模型

刘齐林,曾 玲,曾祥艳

(桂林电子科技大学数学与计算科学学院,广西桂林 541004)

为提高预测模型的精度,提出了一种基于灰色模型和支持向量机的组合预测模型。该模型将累加序列中每个数据分别作为初始条件建立灰色模型,然后对各个灰色模型进行最优组合,通过支持向量机建立最优预测模型,并以成都市1993—2001年航空旅客运输量进行仿真预测实验。实验结果表明,相对于传统灰色模型和灰色神经网络模型,基于灰色模型和支持向量机的组合预测模型提高了预测精度。

灰色模型;支持向量机;时间序列预测

自从1982年邓聚龙提出灰色系统理论[1]以来,研究人员开展了相关理论探索及在不同领域的应用研究。灰色系统理论主要研究“小样本,贫信息不确定”问题,通过序列生成来寻求其变化规律,其最大优点在于所需数据少,预测精度较高,广泛应用在少数据、贫信息的短期预测中[2-3]。现有的灰色模型主要研究模型参数的优化和改进方法[4],以提高灰色模型的预测精度。

1969年Bates和Gtrange系统地研究了组合预测模型[5],相比于单一模型,组合预测模型能较大限度地利用各种模型提供的信息提高预测精度。近年来,章勇高等[6]提出了一种新型灰色神经网络优化组合的风电发电量预测方法,将人工神经网络预测模型与灰色模型有效结合,降低了预测误差。唐万梅[7]提出了灰色支持向量机预测模型,该模型发挥了灰色预测方法中累加生成的优点,增强了规律性,弱化了随机性,通过累减还原得到原始数据预测模型,提高了预测精度。曾振东[8]通过建立网络舆情GM(1,1)模型,运用支持向量机对GM(1,1)模型的预测结果进行残差修正,提高了预测精度。

鉴于此,提出一种基于灰色模型和支持向量机的组合预测模型,该模型将不同初始条件得到的灰色模型的预测值作为支持向量机的输入,输出为一个非线性组合,对样本不断地进行训练和学习,达到一定精度后,再将该最优组合预测模型用于预测,得到最终的预测结果。该组合预测模型避免了传统组合预测模型因采用基于最小二乘法的线性组合过分依赖其预测值及其相应权重的影响,通过支持向量机训练,得到非线性组合输出,减少了组合预测对真实值的偏离[9]。另外,采用灰色模型累加序列中每个数据作为初始条件,利用原始数据的信息,提高了预测模型的精度。

1 改进的灰色预测GM(1,1)模型

GM(1,1)模型是一种最常用的灰色模型[2],由仅含一个变量的一阶微分方程构成。为了说明传统灰色模型在初始条件选取上的不足,现作简要分析。

GM(1,1)模型的白化方程为:

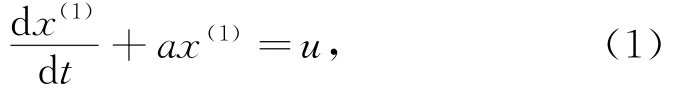
其中a、u为待定参数。求解微分方程(1),

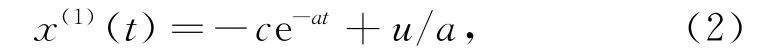
将式(2)离散化,

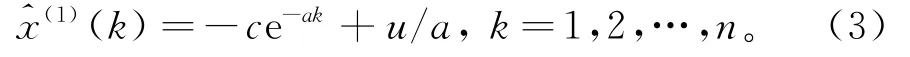
为求解式(3)的c,需要给定初始条件,灰色模型一般将x(1)(1)作为初始条件,代入式(3)得:

将式(4)代入式(3),得到GM(1,1)模型的时间响应序列为:

其中k=0,1,…,n-1。

因此,将累加序列中每个数据分别作为初始条件建立灰色模型[4]。设灰色模型一次累加生成的序列X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),初始条件为x(1)(t)t=m=x(1)(m),m=1,2,…,n,代入式(2)得:

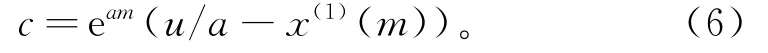
将式(6)代入式(3),得到新的时间响应序列为:

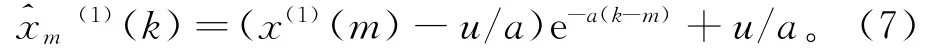
由累减还原得到新的预测公式为:

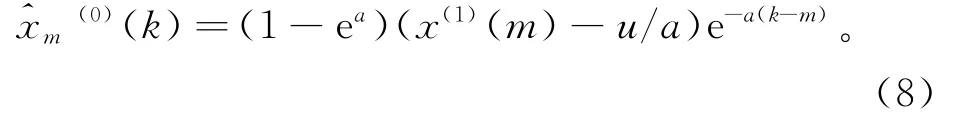
其中:k=1,2,…,n;m=1,2,…,n。

2 支持向量机预测模型

支持向量机是建立在统计学习理论和结构风险最小化基础上的新的机器学习方法[10],具有比较完善的理论基础,在理论上充分保证了模型的泛化性。支持向量机预测模型是寻求输入数据序列与输出数据序列之间的非线性映射关系f,对于给定的训练样本(x1,y1),(x2,y2),…,(xn,yn),xi∈Rn,yi∈R,其中xi为输入数据,yi为对应的输出数据,支持向量机通过非线性映射φ将输入数据序列xi映射到高维特征空间F,在此特征空间进行线性回归:

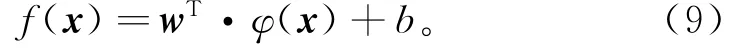
其中:w为权向量;b为偏置量。

由结构风险最小化原则可知,w和b可通过求解下面的优化问题得到:

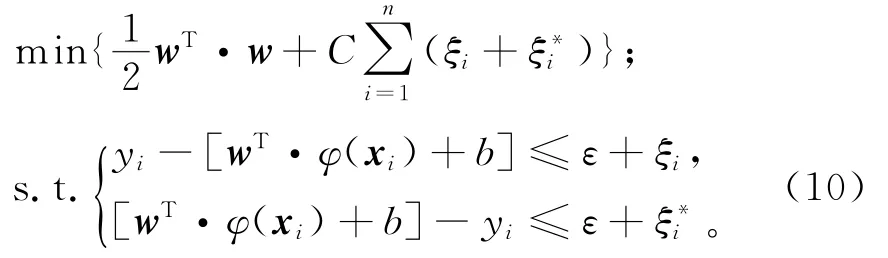
其中:ε为Vapnik用ε不敏感损失函数定义的误差,其控制支持向量的个数和模型的复杂度,提高模型的泛化能力;ξi和ξi*为松弛变量,ξi≥0,ξi*≥0,i=1, 2,…,n;C为惩罚因子。

式(10)为一个凸二次优化问题,可以通过引入拉格朗日函数转化为对偶问题求解:

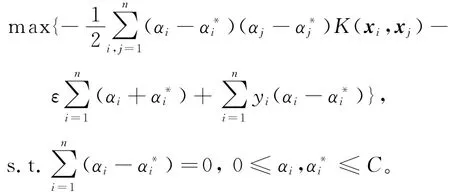
其中,核函数K(xi,xj)=〈φ(xi),φ(xj)〉为高维特征空间中定义的内积,在高维特征空间中使用核函数,不需要知道非线性映射φ的具体形式,降低了模型的计算复杂度。最终得到的非线性预测模型为:

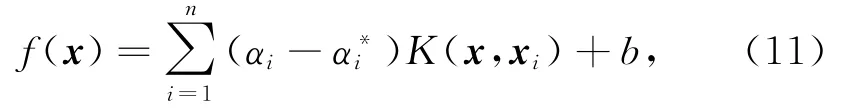
其中αi、α*i为拉格朗日乘子。

3 灰色支持向量机组合预测模型

灰色模型所需数据少,通过累加序列生成,弱化其随机性,增强数据的规律性,但在初始条件选取上存在不足,仅选择一个数据建立灰色模型,未充分利用原始数据中每个数据的信息,如果数据偏差较大,预测精度将大大降低。支持向量机是基于结构风险最小化原则的机器学习方法,具有良好的非线性拟合能力,能充分挖掘各个信息之间的内在关系。灰色支持向量机组合预测模型首先将累加序列中每个数据作为初始条件建立灰色模型,然后将各个灰色模型的预测值作为支持向量机的输入,通过支持向量机训练,得到各个模型的最优组合,运用最优模型进行预测。具体建模步骤为:

1)设原始数据序列X(0)的一次累加生成序列为X(1)=(x(1)(1),x(1)(2),…,x(1)(n)),将累加序列的每个数据作为初始条件建立灰色模型,得到预测值。

2)将灰色模型得到的预测值进行归一化处理,并将归一化处理后的数据作为支持向量机的输入向量。

3)选择适当的核函数,如高斯径向基核函数,通过经验确定支持向量机的参数。

4)对样本进行训练,达到较高精度后,将该模型用于最终预测。

4 数值实验与结果分析

实验采用成都市1993—2001年的航空旅客运输量进行建模[11],预测2002年和2003年的客运量,并与传统灰色模型、灰色神经网络模型的预测精度进行比较分析。

1)选择1993—2001年累加后的数据作为初始条件,建立灰色模型,通过计算,GM(1,1)模型的参数a=-0.099 1,u=138.338 4。

2)将不同初始条件建立的灰色模型记为GM1-GM9模型,通过9个模型得到原始数据序列的拟合值和预测值。将得到的拟合值与预测值进行预处理并归一化,得

其中:z′i为归一化数据;zmax和zmin分别为GM1-GM9模型拟合预测值序列的最大值和最小值。同时将原始数据序列也进行归一化处理。

3)设第1个灰色模型对原始数据(z1,z2,…, z11)的拟合值为(t11,t12,…,t19),预测值为(y11, y12),第2个灰色模型对原始数据的拟合值为(t21, t22,…,t29),预测值为(y21,y22),以此类推,得到第9个灰色模型对原始数据的拟合值为(t91,t92,…, t99),预测值为(y91,y92)。9个灰色模型对原始值x1的拟合值为(t11,t21,…,t91),将(t11,t21,…,t91)作为支持向量机的输入,z1作为支持向量机的输出,其他8个原始值以同样方法构造支持向量机训练样本集,进行支持向量机训练,后2个样本(y11,y21,…,y91;z10)和(y12,y22,…,y92;z11)作为测试集。

4)不断地进行支持向量机训练和学习,最终选择高斯核函数K(x,xi)=exp(-γ‖x-xi‖2)作为核函数,支持向量机其他参数的取值分别为C=1028, γ=0.1,ε=0.01。

3种预测模型的预测值及相对误差如表1所示。从表1可看出,传统灰色模型选择第1个数据作为初始条件,其相对误差为0,拟合效果最好。其他数据的相对误差都比较大,最大相对误差大于10%,说明传统灰色模型选择第1个数据作为初始条件具有很大的缺陷。灰色神经网络模型结合灰色模型和神经网络的非线性拟合,平均相对误差小于传统灰色模型,预测精度有所提高。由于支持向量机基于结构风险最小化原则建模,具有良好的非线性拟合能力和泛化能力,综合运用了单一灰色模型提供的有用信息,灰色支持向量机模型的平均相对误差小于前2种模型,3种模型的平均相对误差分别为6.38%、4.54%、2.42%。

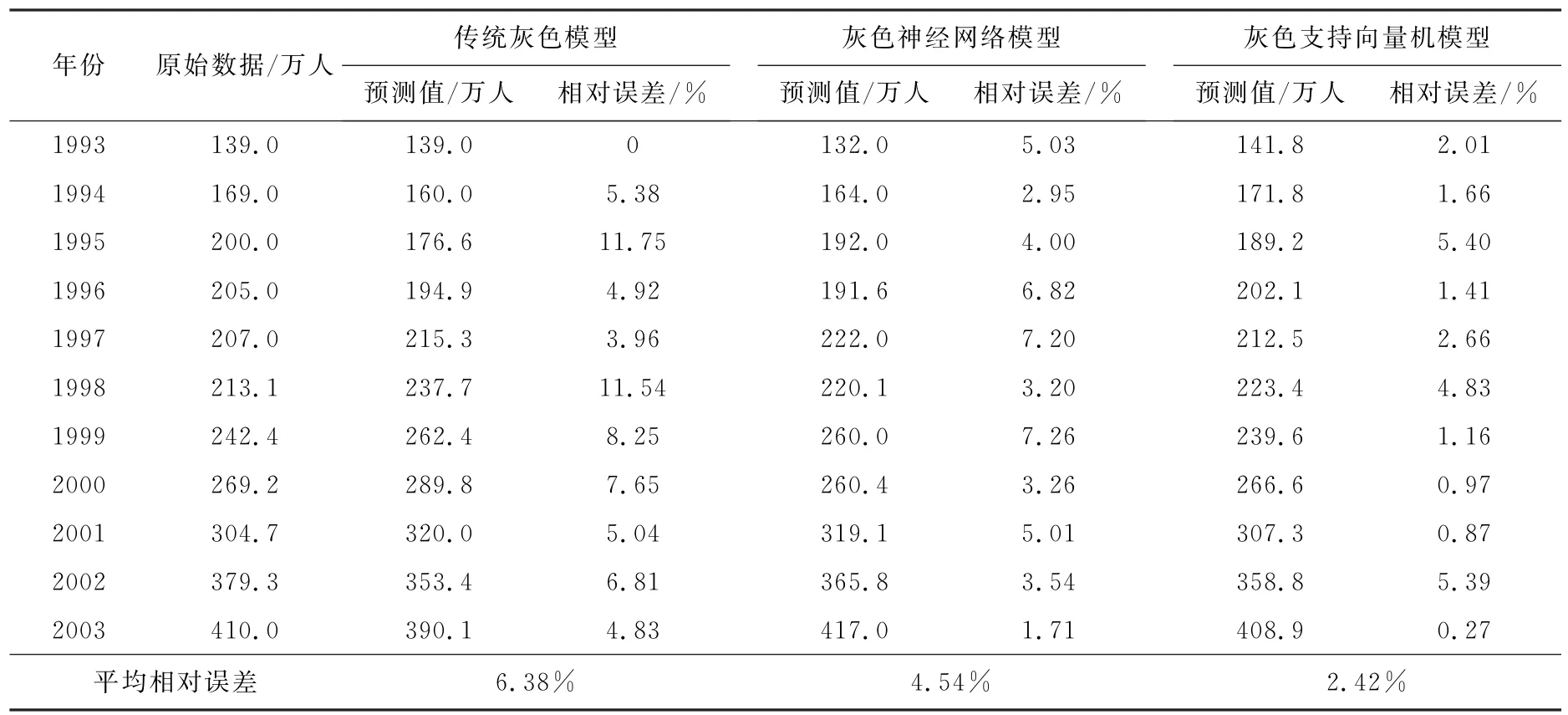
表1 3种预测模型的预测值及相对误差Tab.1 The predictive value and relative error of three prediction models

5 结束语

针对传统灰色模型初始条件选择上的缺陷,改进了传统灰色模型,并结合支持向量机的小样本非线性拟合与泛化能力的优点,提出了一种基于灰色模型和支持向量机的组合预测模型。实验结果表明,与传统灰色模型和灰色神经网络模型相比,灰色支持向量机组合预测模型的预测精度得到较大的提高。

[1] Deng Julong.Control problems of grey systems[J].Systems and Control Letters,1982,1(5):288-294.

[2] 刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].2版.北京:科学出版社,2010:26-39.

[3] 刘思峰.灰色系统理论的产生与发展[J].南京航空航天大学学报,2004,36(2):267-272.

[4] 张大海,江世芳,史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践,2002,22(8):365-368.

[5] Bates J M,Gtrange C W J.The combination of forecasts [J].Operations Research Quarterly,1969,20(4):451-468.

[6] 章勇高,王妍,孙佳,等.基于灰色神经网络优化组合的风力发电量预测研究[J].电测与仪表,2014,51(22):30-34.

[7] 唐万梅.基于灰色支持向量机的新型预测模型[J].系统工程学报,2006,21(4):410-413.

[8] 曾振东.基于灰色支持向量机的网络舆情预测模型[J].计算机应用与软件,2014,31(2):300-302.

[9] Han Dongmei.The comparative study on linear and nonlinear optimal forecast combination methods[J].Information Science,2007,25(11):1672-1678.

[10] Vapnik V N.统计学习理论的本质[M].张学工,译.北京:清华大学出版社,2000:91-118.

[11] 王忠桃.灰色预测模型相关技术研究[D].成都:西南交通大学,2008:26-37.

编辑:曹寿平

A combination forecasting model based on grey model and support vector machine

Liu Qilin,Zeng Ling,Zeng Xiangyan
(School of Mathematics and Computational Science,Guilin University of Electronic Technology,Guilin 541004,China)

In order to improve the accuracy of the forecasting model,a combination forecasting model based on grey model and support vector machine is presented.Each data of the accumulated sequence is used for the initial condition to establish the grey model.Then the optimal combination of the grey model is built,and the optimal prediction model is established by support vector machine.The simulation prediction experiment is conducted according to 1993-2001 air travel passenger transportation volume in Chengdu.The experimental result shows that compared with the traditional grey model and the grey neural network model,the combination forecasting model based on grey model and support vector machine effectively improves the prediction precision.

grey model;support vector machine;time series forecasting

TP18

A

1673-808X(2015)05-0416-04

2015-05-11

广西教育厅科研项目(KY2015YB113);桂林电子科技大学研究生教育创新计划(YJCXS201553)

曾玲(1963-),女,广西荔浦人,教授,研究方向为决策分析、不确定理论及其应用。E-mail:lzeng@guet.edu.cn

刘齐林,曾玲,曾祥艳.基于灰色模型和支持向量机的组合预测模型[J].桂林电子科技大学学报,2015,35(5):416-418.