基于ASP及稳定失败语义的CSP模型检测

左贵征,赵岭忠

基于ASP及稳定失败语义的CSP模型检测

左贵征,赵岭忠

(桂林电子科技大学计算机科学与工程学院,广西桂林 541004)

针对现有模型检测工具对活性描述不足、模型转换复杂,提出一种基于ASP及稳定失败语义的CSP模型检测方法。该方法采用时态逻辑LTL刻画性质,将进程的稳定失败模型和LTL公式转化为ASP,利用ASP求解器验证性质,实现一次运行验证多条性质。实验结果表明,该方法既扩大了基于稳定失败模型的活性验证范围,也避免了不同模型之间的转换。

通信顺序进程;线性时态逻辑;稳定失败语义;回答集程序设计

CSP[1]是由Hoare提出的一种代数语言,主要用于对并发系统进行刻画和验证。随着CSP在并发系统、通信协议等领域的广泛应用,CSP进程的形式化验证成为一个重要的研究课题。目前,CSP验证主要采用定理证明和模型检测,以操作语义和指称语义作为理论基础。

迹模型和稳定失败模型是2种典型的指称语义模型,迹模型描述了进程可执行的行为序列,可用于确定性进程的性质验证。然而,迹模型存在以下不足[2]:1)对所有进程统一采用行为序列描述,不能区分外部选择和内部选择,不能完全描述进程行为。如进程M1=(a→stop),M2=(b→stop),则进程M1| M2与进程的迹集均为{〈a〉,〈b〉}。2)不能验证不同环境下非确定性进程的相关性质。

基于此,Roscoe提出了CSP进程的稳定失败模型[2],该模型扩充了拒绝集描述进程拒绝执行的事件,实现了无发散进程的活性验证。文献[3]给出了一种用于CSP进程精化验证的交互式定理证明器CSP-mrover,在稳定失败模型中,可通过完备度量空间和完全偏序理论验证无边界非确定性的无限状态系统性质。文献[4]针对嵌入CSP迹模型的MVS只能验证进程安全性的问题,提出一种将MVS与CSP稳定失败模型相结合的方法,实现了进程确定性和无死锁的验证。

上述2种方法均采用定理证明,但定理证明的自动化程度不高,不能自动执行,且需要用户有较深的数学造诣,从而限制了它们的应用。主流的模型检测工具FDR通过操作语义将进程转化为迁移系统,通过对应的指称语义实现系统性质的验证。然而,由于涉及到多个模型之间的转换,增加了复杂度。文献[5-7]证明了FDR只能验证部分活性谓词,一些重要的活性谓词可用LTL公式表述,但无法用FDR验证。

为了解决以上问题,提出基于ASP[8]及稳定失败语义的模型检测,采用LTL[9]公式进行性质描述,扩大了基于稳定失败语义所验证性质的范围。此外,也避免进程不同模型之间的转换,降低了计算复杂度。另外,利用ASP求解器可同时验证多条性质。

1 ASP简介

ASP是具有声明特征的知识表示和推理的逻辑设计语言,它的基础是回答集语义,可方便地用于非单调知识的表示和推理,且具有很强的声明性,可对问题自动求解,具有强大的知识表示能力。每个程序是一组规则集合,且规则满足:

a1∨…∨ak←ak+1,…,am,not am+1,…,not an。其中ai为谓词。k＞1的规则称为析取规则,{a1,a2,…,ak}为析取;k=1的规则称为标准规则;k=0的规则称为完整约束;k=n的规则称为事实。

通过ASP解决问题时,利用ASP程序对问题进行描述,使用ASP求解器DLV对描述的ASP程序求解,得到的回答集即为相应问题的解。

2 模型检测框架

基于ASP及稳定失败语义的并发系统CSP模型检测用CSP描述系统的行为,用通用的LTL描述系统性质,然后,将CSP和LTL分别转化为ASP描述和规则,将描述和规则集输入到求解器中,得到对应的回答集,这样“给定系统中,性质能否成立”就改变为“判断回答集中是否存在性质标记”。ASP下基于稳定失败语义的CSP验证框架如图1所示。

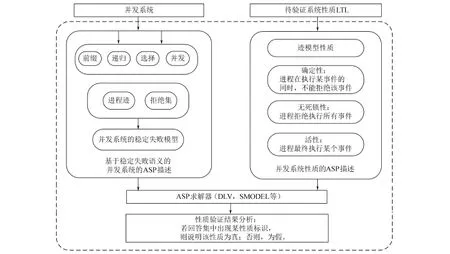
图1 ASP下基于稳定失败语义的CSP模型检测框架Fig.1 CSP verification framework based on ASP and stable failure semantics

将该框架划分为两部分设计与实现:

1)CSP并发系统及其稳定失败模型的ASP描述和对应规则。定义谓词实现进程的描述,根据这些谓词定义对应稳定失败模型(包括进程的迹和拒绝集)的生成规则。其中,进程包括基本进程和并发组合,尤其是内部选择和外部选择的区分尤为重要。

2)LTL公式到ASP规则的转换。稳定失败模型可描述事件发生的必须性和可能性,LTL中存在公式a描述事件a一定发生。因此,增加公式available a描述事件a可发生,但不是必须发生。最后,给出LTL公式稳定失败语义下的ASP描述。

3 CSP稳定失败模型的ASP描述

CSP并发系统由进程通过不同的算子组合而成,针对不同算子,分别定义对应的谓词描述及规则,从而通过组合实现并发系统的ASP描述及稳定失败模型的生成。

进程的稳定失败模型一般包括进程的迹(可执行行为序列)和拒绝集(可拒绝的事件集合),因此,分别针对迹和拒绝集构造不同的谓词及规则,从而实现稳定失败模型的描述。

文献[10]已定义了所需的大部分符号谓词,将其扩充到稳定失败模型中,需要加入一些新的谓词和规则,ASP谓词如表1所示。

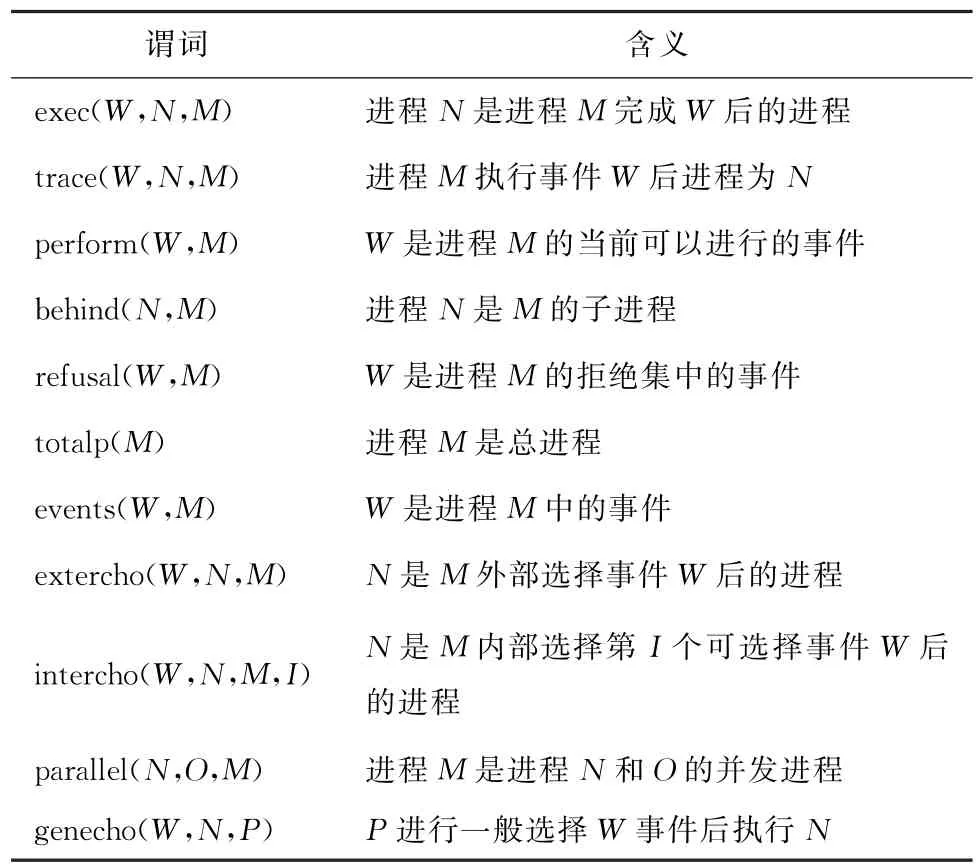
表1 ASP谓词Tab.1 ASP predicates

3.1 前缀和递归进程

前缀进程M具有如下形式:

M=x→N,意味着M首先完成事件x,接着进行N的行为,其中,α(x→N)=αN=αM。

根据进程的ASP谓词推导进程的迹:

R1 trace(W,N,M):-exec(W,N,M)。

已知进程M的谓词描述,利用ASP技术生成M的拒绝集,步骤为:

1)计算M的事件集;

2)由M的迹可推出M的可执行的事件。

生成ASP规则如下:

R2 events(W,M):-trace(W,N,M)。

R3 events(W,N):-trace(W,O,N),behind (N,M)。

R4 behind(M,N):-exec(W,M,N)。

R5 perform(W,M):-trace(W,N,M)。

R6 refusal(W,M):-events(W,M),not exec (W,M)。

递归进程是一种特殊的前缀进程,例1证明了递归进程拒绝集由前缀进程拒绝集的生成方法生成。

例1 进程M的CSP描述为:

M=dseat→upStick→meal→dStick→useat→M。

对M进行谓词表示:

{exec(dseat,m0,m).exec(upstick,m1,m0).exec(meal,m2,m1).exec(dstick,m3,m2).exec(useat, m,m3).totalp(m).}。

该进程描述与上述规则输入到ASP回答集求解器DLV中,输出回答集中包含M的稳定失败集的信息如下:

{totalp(m).refusal(upstick,m).refusal(meal, m).refusal(dstick,m).refusal(useat,m).}。

3.2 选择进程

3.2.1 外部选择

外部选择进程具有如下形式:

M=(x→N|y→O)。

其执行规则为:若环境选择事件x,则进程执行N;若环境选择事件y,则进程执行O。明显地,M的迹需要包括所有可能发生的行为。

例2 顾客投入2元硬币后,选择售出大瓶饮料,或售出小瓶饮料后找零1元硬币。该进程用CSP描述为:

V=(enter2c→large→V|enter2c→small→exit1c→V)。

图2为进程V的迹及其ASP谓词描述。其中, {extercho(large,v,v1)}表明进程在选择运算时,已经执行了被选择的事件。图3为基于已定义的ASP谓词计算进程V拒绝集的大致步骤。

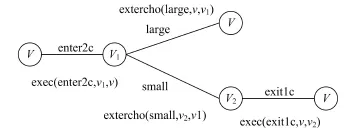
图2 进程V的迹及其ASP谓词描述Fig.2 The traces and ASP predicates of process V

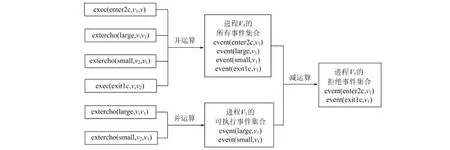
图3 外部选择V的拒绝集求解步骤Fig.3 The refusal sets solving steps of external choice V

因此,外部选择进程的迹推导规则需要在上述规则上增加:

R7 trace(W,N,M):-extercho(W,O,M)。

外部选择M的拒绝集与前缀算子类似,都是所有事件集与可执行的事件集的差,差别在于前缀进程的可以执行的事件只有一个,而M包括所有可能选择的事件。M的拒绝集定义如下:

R8 refusal(W,M):-events(W,M),refusal (W,M),extercho(W,N,M)。

3.2.2 内部选择

内部选择进程具有如下形式:

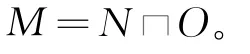
表示进程M或按N的行为执行,或按O的行为执行,但它不允许由环境决定;相反,由进程内部选择。

例3 一台自动售货机在投入2元硬币后,随机选择售出大瓶饮料,或售出小瓶饮料后找零1元硬币。该进程可描述为:

图4为进程S的迹及其ASP谓词描述。其中, {intercho(large,s,s1,1)}除了表明进程在进行选择时已经执行被选择事件,还给出了编号,为后面计算拒绝集做准备。同时,如果只看可执行的行为序列,其与例2中V一致。但S的拒绝集不止一个,且各不相同。图5为基于已定义的ASP谓词计算进程S拒绝集的大致步骤。已知内部选择的迹推导规则和外部选择类似: R9 trace(W,N,M):-intercho(W,N,M,I)。进程M的拒绝集是N和O的拒绝集的组合,利用ASP技术生成步骤如下:

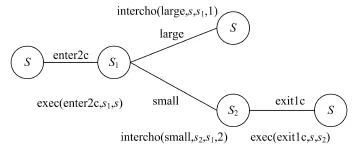
图4 进程S的迹及其ASP描述Fig.4 The traces and ASP predicates of process S

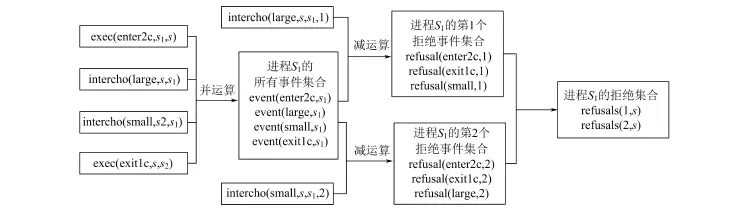
图5 内部选择S的拒绝集求解步骤Fig.5 The refusal sets solving steps of internal choice S

1)计算进程N和O的拒绝集;

2)由N和O的拒绝集构成M的拒绝集。

因此,一般选择进程的拒绝集求解规则如下:

R10 refusal(W,I):-events(W,M),not initial (W,I).initial(W,I):-intercho(W,N,M,I)。

R11 refusals(I,M):-intercho(W,N,M,I)。

3.2.3 一般选择

进程M□N或按照进程M执行,或按照进程N执行,它提供给环境M和N的事件,由环境选择具体哪个进程。若事件相同,其等同于M|N;若事件不同,等同于MN。

一般选择的迹和非确定选择的迹相同,其迹推导规则如下:

R12 trace(W,N,M):-genecho(W,N,M,I)。但拒绝集和非确定选择的拒绝集不同,是N和O的拒绝集的交集,因此,其拒绝集求解规则如下:

R13 refusal(W,M):-refusal(W,N),refusal (W,O)。

3.3 并发组合

并发进程具有如下形式:

M=N‖O,要求进程N和O共同完成相同事件,分开完成不同的事件。根据CSP定义的并发规则,将M转化为顺序进程,即等价于前缀进程。因此,并发进程的迹推导规则为:

1)基于并发规则求解M的执行序列;

2)根据M的执行序列可计算M的迹。

M的拒绝集是2个子进程N和O拒绝集的并集,求解步骤如下:

1)由前缀进程的拒绝集定义分别生成子进程N和O的拒绝集;

2)由N和O的拒绝集计算M的拒绝集。

因此,并发进程的拒绝集推导规则如下:

R14 refusal(W,M):-events(W,M),refusal (W,M),not parallel(N,O,M)。

R15 refusal(W,M):-refusal(W,N),parallel (N,O,M)。

R16 refusal(W,M):-refusal(W,O),parallel (N,O,M)。

4 系统性质LTL公式的ASP生成

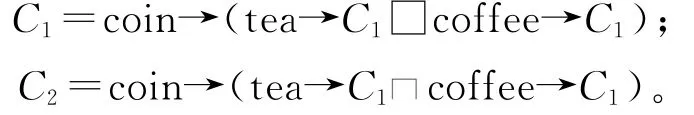
性质描述:售货机在顾客投入一枚硬币后,对顾客既提供咖啡的选择,也提供茶的选择。该性质用LTL描述为:

ϕ=□(coin⇒○(available tea∧available coffee))。其中,a⇒ϕ的形式是┐a∨(a∧ϕ)的简写。进程C1满足公式ϕ,但进程C2不满足。available可描述类似C1和C2的不同之处,但available并不表示阻止其他事件发生。如进程

C3=coin→(tea→C3□coffee→C3□chocolate→C3)同样满足ϕ。

下述例子更能区分a和available a的不同之处(a包含available a):

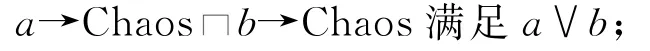
主流的模型检测工具采用CSP进程形式描述性质规约,相较于LTL公式,其表达能力有限且通用性不强,特别是对活性的描述不足。为扩大活性验证范围,采用LTL进行规约。LTL公式可通过以下结构生成:

1)原子谓词。描述单个状态。

2)连接词。通常有析取∨、合取∧和否定┐。

3)时态词。○ϕ(“下一个ϕ”):在下一个状态,ϕ将成立;□ϕ(“总是ϕ”):在所有后继状态中,ϕ成立;◇ϕ(“最终ϕ”):在后继某些状态中,ϕ成立。

LTL公式说明了进程执行需要满足的性质。当M每步操作都满足ϕ时,记为:M⊧ϕ。

在CSP中,描述的是通信系统,进程事件的发生取决于外部环境,因此,为了区分环境选择和非确定性选择,加入了事件的可能性(available)。定义以下原子公式。

a:环境执行且只执行事件a。

available a:环境可执行事件a,但也可执行其他事件。deadlocked:进程是死锁的,等价于∧a∈Σ┐a。live:进程有活性,即非死锁,等价于∨a∈Σ┐a。true,false:为真,或为假。

例4说明了加入available的原因。

例4 进程C1描述售货机在接收一枚硬币后,由顾客选择咖啡或茶,而C2描述售货机在接收一枚硬币后,内部选择提供给顾客咖啡或茶。进程C1和C2用CSP描述为:

a→Chaos□b→Chaos满足(a∧available b)∨(b∧available a)。

为简化起见,定义LTL为:

ϕ∈LTL::=true│false│a│available a│live│deadlocked;

│ϕ1∧ϕ2│ϕ1∨ϕ2│┐ϕ│○ϕ│□ϕ│◇ϕ。

给出稳定失败语义下,进程M的LTL公式对应的ASP规则描述:

ϕ=a⇔ϕ(M):-trace(a,N,M),not refusal(a, M);

ϕ=available a⇔ϕ(M):-not refusal(a,M);

ϕ=live⇔ϕ(M):-dlf(M),totalp(M);

ϕ=deadlocked⇔ϕ(M):-not dlf(M);

ϕ=ϕ1∧ϕ2⇔ϕ(M):-ϕ1(M),ϕ2(M);

ϕ=ϕ1∨ϕ2⇔ϕ(M):-ϕ1(M).ϕ(M):-ϕ2(M);

ϕ=┐ϕ1⇔ϕ(M):-notϕ1(M);

ϕ=○ϕ1⇔ϕ(M):-ϕ1(N),next(N,M) ϕ(M):-deadlocked(M);

ϕ=□ϕ1⇔ϕ(M):-not f.f:-notϕ1(N),behind (N,M)ϕ(M):-ϕ1(N),not f.f:-ϕ1(N), notϕ2(O),behind(N,O),behind(O,M);

ϕ=◇ϕ1⇔ϕ(M):-ϕ1(N),behind(N,M)。

其中,系统活性live的ASP推导规则还包括:

dlf(M):-events(W,M),not refusal(W,M);

dlf(M):-exec(W,N,M),dlf(N);

dlf(M):-dlf(N),dlf(O),genecho(N,O,M)。

在分别给出进程M稳定失败模型的ASP规则以及稳定失败语义下LTL公式转化为ASP的规则之后,检测该进程性质的流程为:

1)对M用ASP描述,加入其稳定失败语义的ASP规则,可生成稳定失败模型下的谓词描述。

2)对给定性质用LTL公式表示,根据对应的ASP转换通用规则,将其转换为含性质标记的ASP规则。

3)将上述ASP谓词及规则输入到回答集求解器DLV中,运行该求解器,观察得到的回答集中是否包含性质标记。

5 实验分析

以思想家就餐模型为例,n位思想家围着一张桌子,每对相邻思想家中间有一根筷子,思想家只拿左边或右边的筷子,一位思想家只有拿到2根筷子才可进食。假设每位思想家都先拿左手边的筷子,且只要他们拿起来,则直到进食后才能放下。思想家的行为用CSP描述为:

Mj=dseat→upStick.j→upStick.j→meal→dStick.j→dStick.j→useat→Mj。

以3位思想家为例,则j∈{1,2,3},将3位思想家进行并发运算构成进程M。模型待验证性质如下:

1)一位思想家不能同一时间拿2根筷子;

2)该模型具有确定性;

3)该模型存在死锁;

4)该模型是活性的;

5)只要某位思想家拿到筷子,他一定能吃到东西。

首先,用LTL公式表示上述性质,然后,根据LTL的转化规则将其表示为ASP规则,待验证性质的LTL和ASP描述如表2所示。

表2 待验证性质的LTL和ASP描述Tab.2 LTL and ASP descriptions of the verified properties

把A∪B1∪B2∪B3∪B4∪B5以及规则R1~ R16和并发规则输入到回答集求解器DLV中。图6为该模型性质验证回答集。

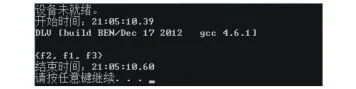
图6 该模型性质验证回答集Fig.6 Answer sets of the model properties verification

利用filter=f1,f2,f3,f4,f5语句使得回答集只显示指定性质。对于该并发系统,在3位思想家同一时间拿起左手边筷子时,开始陷入死锁,每位思想家都无法进食,因此该系统不是活性的,只包含性质标记f1、f2、f3,不包含f4、f5,验证结果与事实一致。

为避免死锁的产生,规定第3位思想家先拿右手边筷子:

M3=dseat→upStick.1→upStick.3→meal→dStick.1→dStick.3→useat→M3。

更改对应的ASP描述为:

{exec(dseat,m31,m3).exec(upstick1,m32, m31).exec(upstick3,m33,m32).exec(dstick1,m34, m33).exec(dstick3,m35,m34).exec(useat,m3, m35).}。

此时更改集合A中的M3对应的ASP谓词描述,其他不变,输入DLV求解器中,调整后的思想家就餐模型性质验证回答集如图7所示。

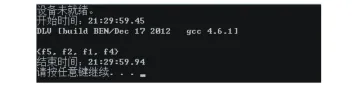
图7 调整后的思想家就餐模型性质验证回答集Fig.7 Answer sets of the modified dining philosophers model properties verification

性质标记f1、f2、f4、f5出现在回答集中,即调整后的思想家就餐模型不仅包含性质f1和f2,且该模型是活性的(f4,f5),不包含性质f3。

以上实例说明了基于ASP及稳定失败语义的并发系统性质验证方法的可行性和有效性,且可同时验证多条性质。

6 结束语

提出基于ASP及稳定失败语义的CSP并发系统模型验证,减少了不同模型之间的转换,利用LTL公式描述系统性质,具有更强的通用性。实验结果表明,该方法可实现系统活性的验证,且可验证活性范围更广,同时,一次验证多条性质,提高了验证效率。下一步工作将考虑对稳定失败模型进行抽象,扩大待验证系统规模。另一方面扩充到失败发散模型,研究并发系统的活锁问题。

[1] Hoare C A R.Communicating Sequential Processes[M/ OL].http://www.usingcsp.com/cspbooks,2004:1-112.

[2] Roscoe A W.The Theory and Practice of Concurrency [M].Prentice-Hall.United States:Prentice Hall,2005: 1-100,183-220.

[3] Isobe Y,Roggenbach M.A generic theorm prover of CSP refinement[J].Lecture Notes in Computer Science,2005(3440):108-123.

[4] Wei K,Heather J.Embedding the stable failures model of CSP in PVS[J].IFM,2005(3771):246-265.

[5] Roscoe A W.On the expressive power of CSP refinement[J].Formal Aspects of Computing,2005,17(2): 93-112.

[6] Murray T.On the limits of refinement-testing for model-checking CSP[J].Formal Aspects of Computing,2013 (2):219-256.

[7] Robinson T G,Armstrong T,Boulgakov P,et al.FDR3-A modern refinement checker for CSP[C]//20th International Conference on Tools and Algorithms for the Construction and Analysis of Systems,2014:1-14.

[8] Baral C.Knowledge Representation,Reasoning,and Declarative Problem Solving[M].Cambridge:Cambridge Univerdseaty Press,2003:5-64.

[9] Moshe Y V.Branching V.Linear time:final showdown [J].Lecture Notes in Computer Science,2011(2031):1-22.

[10] 赵岭忠,司徒凌云,翟仲毅,等.基于ASP的CSP进程描述与组合研究[J].计算机科学,2013,40(12):133-140.

编辑:梁王欢

CSP model checking based on ASP and stable failure semantics

Zuo Guizheng,Zhao Lingzhong
(School of Computer Science and Engineering,Guilin University of Electronic Technology,Guilin 541004,China)

Aiming at lack of activity description and the complexity of models transition of CSP model checkers,CSP model checking based on ASP and stable failure semantics is proposed.In this method,the properties are specified by linear temporal logic(LTL),the description of CSP system and LTL properties are implemented with answer set programming(ASP), then multiple properties are verified in one execution of ASP solvers.The experimental result shows that the method expands the scope of liveness properties based on stable failure model,and prevents transition from different models.

communication sequence process(CSP);linear temporal logic(LTL);stable failure semantics;answer set programming(ASP)

TP311

A

1673-808X(2015)05-0401-07

2015-03-18

国家自然科学基金(61262008,61100186);广西可信软件重点实验室基金(KX201113)

赵岭忠(1977-),男,河南社旗人,教授,博士,研究方向为形式化技术。E-mail:zhaolingzhong163@163.com

左贵征,赵岭忠.基于ASP及稳定失败语义的CSP模型检测[J].桂林电子科技大学学报,2015,35(5):401-407.