G-S模型下的协同过滤算法

顾 凯,刘建明

G-S模型下的协同过滤算法

顾 凯1,刘建明2

(1.桂林电子科技大学电子工程与自动化学院,广西桂林 541004; 2.桂林电子科技大学计算机科学与工程学院,广西桂林 541004)

针对协同过滤算法忽视供应商偏好、存在稀疏矩阵导致准确率低的现象,提出一种改进的协同过滤算法。利用改进的相似度计算方法填充评分矩阵,计算目标用户的评分,将目标用户评分作为G-S算法的输入项,得到消费者、供应商的匹配结果。仿真结果表明,算法具有较高的满意度和准确率。

协同过滤算法;满意值;Pareto最优;信息熵

推荐系统已广泛应用在电子商务系统中,它能为消费者找到较为准确的购买目标,大大提升了供应商的销售额[1]。旅游网站Priceline消费者主动出价的模式考虑到了双方的利益。

协同过滤算法是应用最为广泛的推荐算法。为了解决该算法中出现的稀疏矩阵,有学者提出利用评分均值填充的算法,还有学者提出一种基于项目评分的填充算法[2]。

随着消费者、供应商的快速增加,而用户-项目评分矩阵的数据严重稀疏,传统的填充方法计算得到的预测评分不准确,出现推荐准确率低的问题[3],同时传统推荐算法还存在忽视供应商需求的问题。鉴于传统的填充方法得到的预测评分不够准确,提出一种综合填充算法,该算法考虑了共同评分数量、评分背景两者对相似度的影响。为解决忽视供应商利益的问题,引入Pareto最优的概念,在电子商务平台上, Pareto最优状态要求同时考虑消费者和供应商的满意值。G-S算法能求Pareto最优解,其最早出现在Shapley的基础理论研究[4-5],后来Roth将其应用于市场实践[6-7]。G-S算法是针对双方数量相同的情况,因此提出一种改进的G-S算法来解决电子商务中消费者的数量要远大于供应商的问题。

1 G-S模型

G-S算法应用在双边匹配市场中,照顾到参与双方的利益,在理论和实践中被验证具有稳定性。

G-S的流程用如下语言表示:

while 消费者集合B中存在消费者b_i

在b_i还未发申请的供应商中选择满意值bigf最高的一个供应商s_j发出意向

if s_j未收到项目申请or意向个数小于库存then

b_i与s_j结合组成(b_i,s_j)

else//s_j已经与b_k组成组合(b_k,s_j)

if g(s_j,b_k)＞g(s_j,b_i)//s_j更喜欢b_k

then

b_i进去下一轮循环

else b_i与s_j组成组合(b_i,s_j)

b_k变成被拒绝者,进入下一轮循环

//供应商s_j更喜欢消费者b_i

end if

end if

end while

最终返回的配对集合矩阵S是一个稳定的匹配,此算法的关键是要得出消费者的偏好,将协同过滤算法产生的推荐作为G-S算法的输入内容。

2 推荐算法的实现

2.1 传统相似度

求用户对项目的评分,关键是求相似度。从相似度角度看,流行的推荐算法包括基于内容推荐算法和基于协同过滤的推荐算法。内容推荐的特点是匹配准确、推荐更多新项目,但存在覆盖率低、项目特征提取困难等问题。协同过滤包括基于用户的协同过滤和基于项目的协同过滤。结合用户购买行为的特点,采用基于项目的协同过滤进行预填充,采用基于用户的协同过滤计算目标用户得分。项目之间的相似度采用修正的余弦相似度计算效果较好[8],计算公式为:

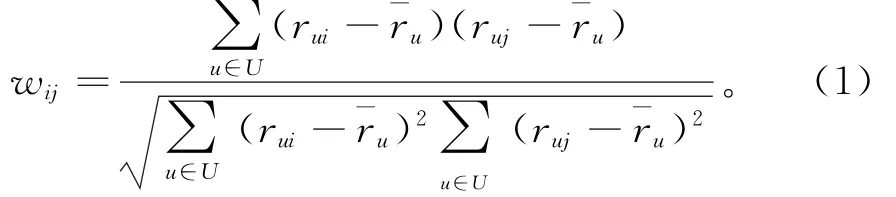
其中:i、j分别为不同的项目;¯ru为在评分矩阵中用户的平均评分;rui、ruj分别为同一用户u对不同项目i、j的评分。

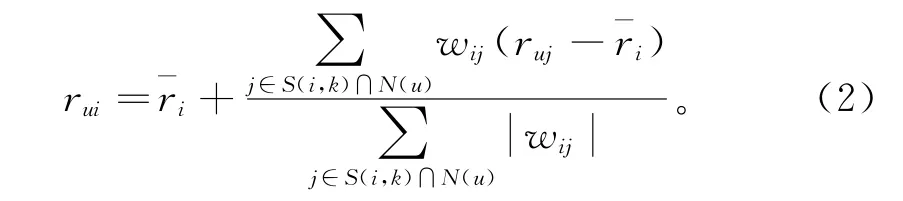
用户对项目的评分公式为:其中:S(i,k)为与项目i最相似的k个项目集合;N (u)为有过评分的项目集合或对有过评分的用户集合。

2.2 传统方法存在的问题

表1为用户对项目的评分矩阵。从表1可见,用户U2缺少对项目I1的评分,但由项目I1、I3之间相似的特性可知,U2对项目I1的评分为3。因此,可先根据项目相似度进行填充。

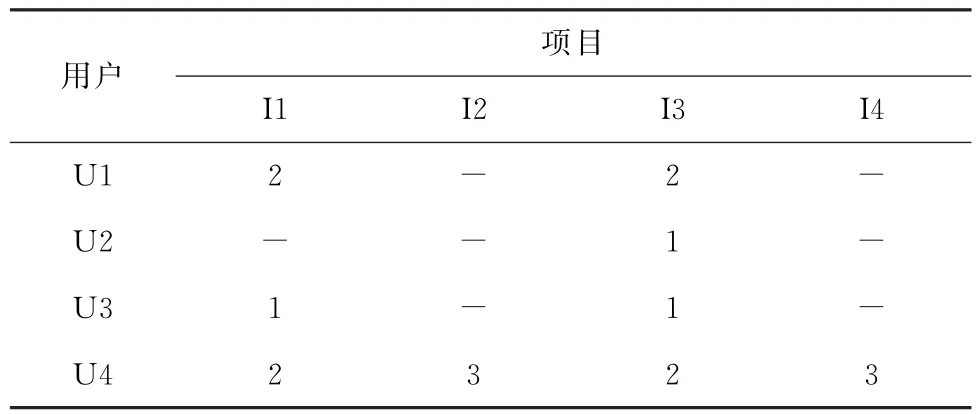
表1 评分矩阵Tab.1 The matrix of rate value

因为存在稀疏矩阵,导致相似度计算不准确,为此,人们进行了大量的研究,常用的方法是对评分矩阵进行预填充,设定一个固定的缺省值,取用户或项目的平均分,文献[9-10]提出了一种信任度传播的评分填充算法,文献[2]提出了基于项目评分预测的协同过滤推荐算法,文献[11]提出了基于概率知识的评分填充算法。这些方法均未考虑项目属性出现的情境,比如在价格高的项目中,高价格就没有什么代表性,计算的相似度自然不准确;如果周围的项目都是一种品牌,出现了其他品牌就非常容易区分,计算的相似度自然对类的区分很有贡献,文献[12]提出一种基于用户评分差异的协同过滤算法。

2.3 改进的基于项目相似度填充

1948年,香农提出了“信息熵”的概念,用数学语言阐明了概率与信息冗余度的关系。这里用信息熵表示信息的稳定性,若信息分布越均匀,则信息熵越大,若属性越集中,则信息熵越小。

在相似度的基础上,加入信息熵的概念,相似度的计算结果会更加准确。假设项目的一个属性f有多个种类,多种取值属性值vfm构成属性集合V(f) ={vf1,vf2,…,vfm}。对于离散的项目属性容易处理,而对于连续型的属性,要为每一区间的属性规定相应的名称。以项目的价格为例,把价格区间划分为奢侈、昂贵、经济、便宜4类,相应的取值为:

其中:n(vfm)为属性fm出现的次数;n为项目的数量。项目价格的信息熵为:

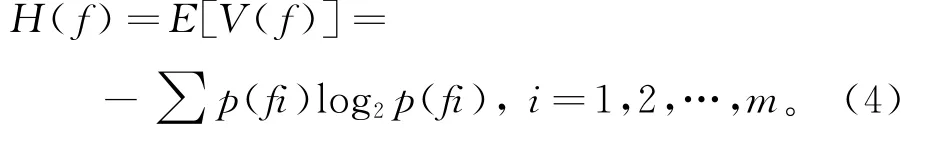
其中p(fi)为fi出现的概率。信息熵越大,表示价格4种属性分布越平均,项目价格属性便于区分,否则,价格属性没有区分的必要。改进后的相似度为:

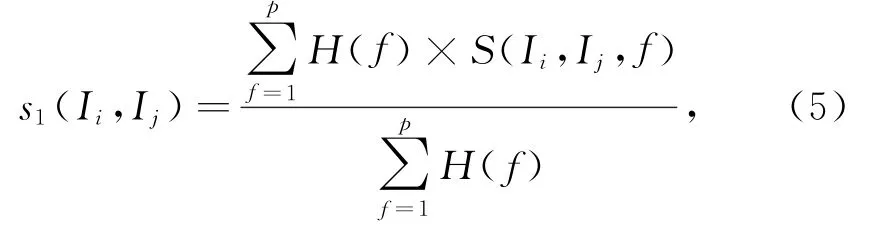
其中:p为项目数量;s1(Ii,Ij)∈[0,1];

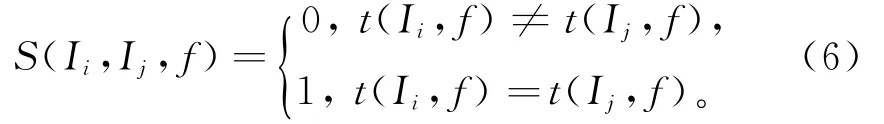
S(Ii,Ij,f)表示项目Ii和Ij属性值是否相同,若相同为1,否则为0;t(Ii,f)和t(Ij,f)表示项目Ii和Ij,的属性f值,s1越大,项目的此属性越有区分力,说明在此情境下此属性越能代表2种项目的相似度。

项目相似度还应考虑拥有相同属性的用户数量。表1中项目I1和I3共同评分的用户数量更多,它们可能拥有更高的相似度,而根据传统的相似度求解方法,I2、I4的相似度则更高,稀疏矩阵导致忽视共同评分数量的现象更加明显,因此求相似度应该考虑共同评分的用户数量。受Jaccard系数启发,加权共同评分数量的相似度:

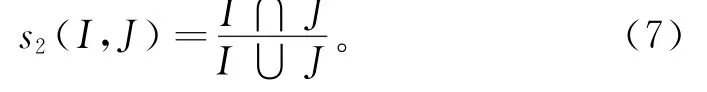
式(7)中分子表示两项目有共同评分的用户数量,分母表示用户总数。s2在[0,1]内越大,表示共同评分的数量越大,即2个消费者的相似度越高。

对s1、基于相同项目评分数量的s2及基于项目评分的修正的余弦相似度进行加权,得到最后的相似度公式为:

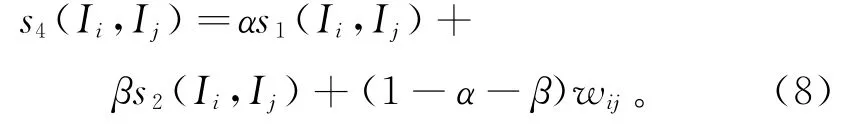
其中,α和β为调节系数,可调节修正的余弦相似度、s1系数和基于共同评分数量的相关系数三者的比重, α∈[0,1]。

根据最终的相似度系数s4对未评分的项目进行填充,

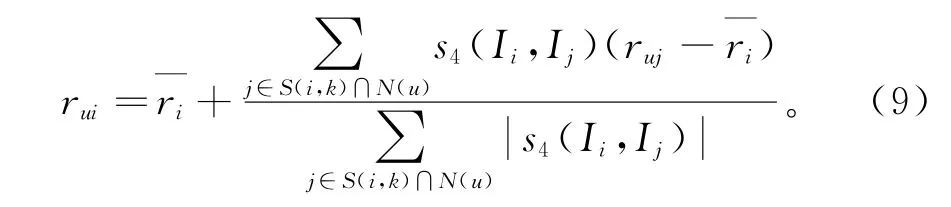
2.4 基于用户邻域相似度的评分预测

人的行为受社会化的影响[13],在评分填充后计算用户相似度,根据式(2)计算目标用户对项目的预测评分rui,再根据评分高低产生推荐。

3 在改进的G-S框架下双边算法的实现

3.1 双边算法的实现步骤

传统推荐算法忽略供应商的偏好,受双边算法的启发,利用改进的G-S算法解决此问题。假设有m个消费者、n个供应商,项目有f个属性。推荐算法在G-S框架下实现的具体步骤为:

1)改进的协同过滤算法得到的推荐作为G-S算法中消费者的偏好。

2)消费者给出相关偏好rb,并根据项目属性ps计算适合值bijgf,加入消费者对属性的权限值wif,得出满意值bijg,系统按满意值高低依次向供应商发出意向。

3)根据供应商要求rs和消费者属性pb计算Sji,加入购买数量计算总满意度Gji。供应商对有意向的买家进行排序得到矩阵O。若卖家有库存,则预留消费者;若无库存,则拒绝排序最靠后的买方,被拒绝的买方向下一个志愿发出意向。

4)依次类推,直至向所有的买方都发出意向,一轮匹配结束。

5)下一轮循环开始,直至完成所有匹配或达到规定的循环次数。

3.2 消费者满意值

软约束条件指的是在一定的范围内都可以接受的条件,通过计算满意值和满意度判定偏好程度。而软约束有越大越好型和越少越好型,比如项目的配置和价格。消费者对项目属性可分以下几种:

1)越大越好型。消费者选择项目时希望项目的配置、质量越高越好。引入适合值函数bijgf表示消费者i对于供应商j的项目g的属性f的满意度,用-1表示供应商的项目属性pjgf小于消费者对该项目属性的最低要求rif,min,1表示供应商的项目属性pjgf大于等于消费者的最高要求rigf,适合值为:

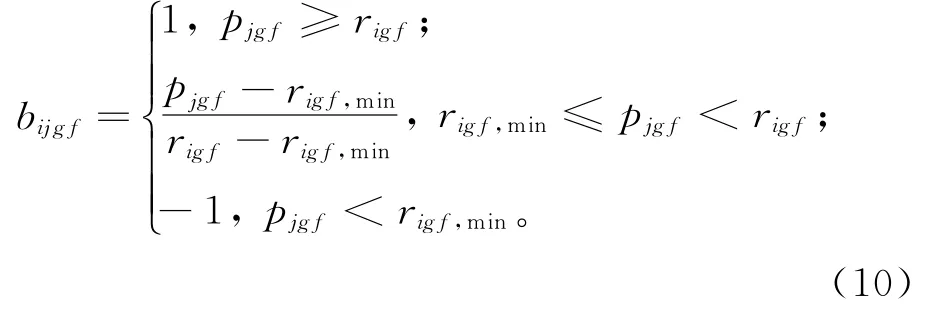
2)越少越好型。消费者对于项目的价格越低越好,用-1表示供应商的项目属性高于消费者对于该项目属性的上限rigf,max,1表示供应商的项目的属性值小于消费者的下限要求,适合值为:

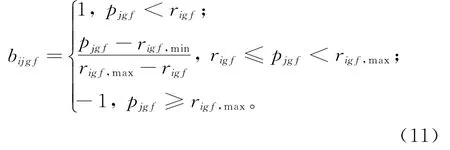
消费者根据自己的满意值,由大到小依次向心仪的供应商发出购买意向,满意值计算式为:

3.3 供应商满意值

供应商同样对消费者有偏好,他们往往关心消费者的信用,引入适合值Sjigf表示供应商对消费者的偏好,用1表示消费者的信用度pigf大于供应商的最好心理值rigf,-1表示消费者的信用度小于供应商的最差心理值rjgf,min,供应商满意值为:

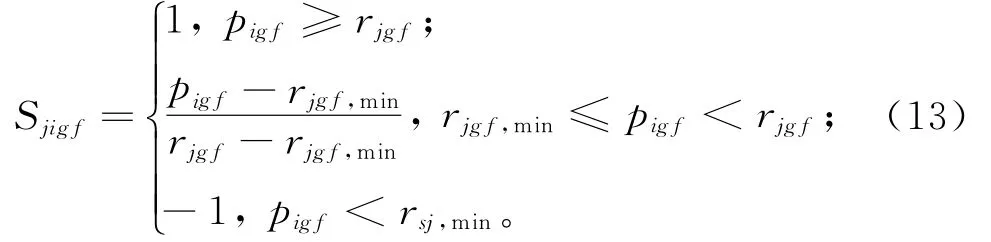
3.4 满意度

匹配过程会出现一个供应商对应多个消费者,购买数量作为一个权值参与计算总满意值Gji,并按Gji大小对消费者进行排序。供应商把对自己有意向的消费者按照偏好矩阵O进行排序,供应商库存充足,则接受所有消费者;一旦出现需求大于库存m的情况,供应商就要剔除排序靠后的消费者,被剔除的消费者进入下一轮循环。满意度计算式为:

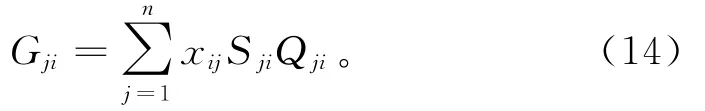
其中:

4 仿真实验与分析

4.1 实验评价标准

采用平均绝对误差EMA作为评价推荐算法预处理阶段的指标,

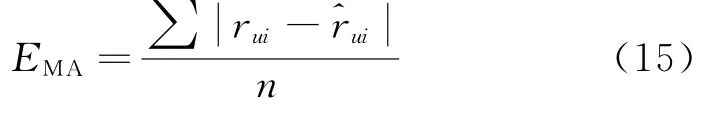
定义参与率为最终匹配方案与推荐系统列表之间对应的比值:

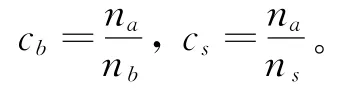
其中:cb为消费者参与度;cs为供应商参与度;na为G-S算法匹配成功的项目数量;ns为预推荐给消费者的项目数量;nb为消费者总数。

4.2 仿真数据

采用MovieLens数据集,其包含用户对自己看过的电影进行评分,分值为1~5。采用小规模库,有943个用户对1682部电影作的10 000次评分。为了验证推荐算法的准确性,实验分别在10、20、30、40四种邻居规模上进行,将传统的协同过滤推荐算法、基于项目评分相似度填充的算法与改进的算法进行对比。首先对数据进行随机采集,平均分成8份,选取其中的7份作为训练集,1份作为测试集,循环3次,取平均值作为结果。采用α、β均为0.1的情况下对算法进行试验。

为验证算法能同时提高消费者和供应商的满意度,设定消费者的偏好内容是项目价格,供应商更在意消费者的信用度,通过将各自的要求与对方的属性比较,便可计算出偏好程度。匹配方案加入先前得出的偏好程度,便可计算出最终的满意值。根据改进的G-S算法的要求,假设有9个消费者和3个供应商。表2为供应商对消费者信用的要求和项目属性,表3为消费者对项目的要求和自身信用指数。

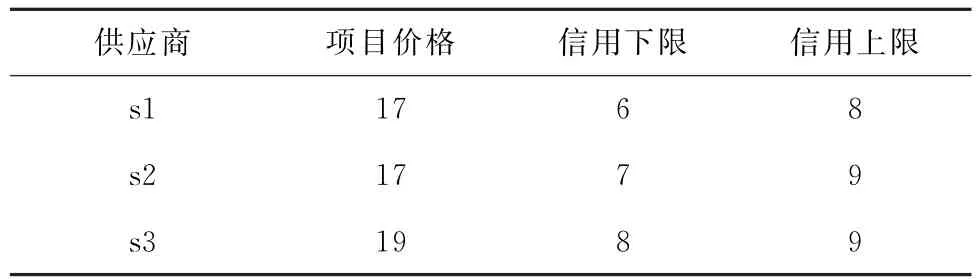
表2 供应商对信用的要求和项目价格属性Tab.2 The credit requirement of suppliers and commodity price

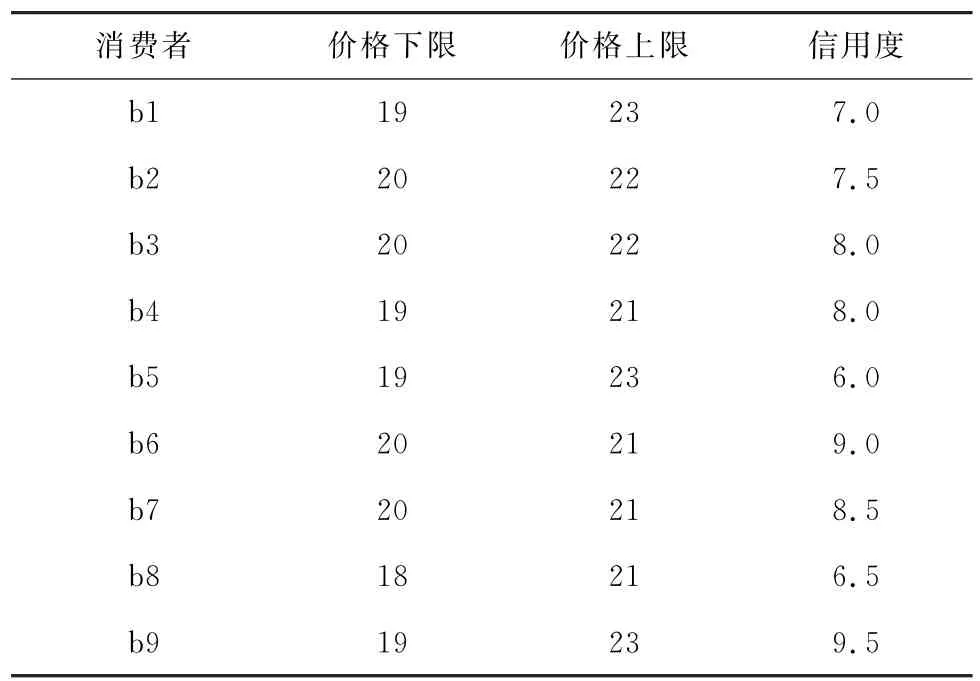
表3 消费者对项目的要求和自身信用指数Tab.3 The commodity requirement of consumers and credit value

计算得到的消费者对供应商满意值如表4所示,供应商对消费者满意值如表5所示。

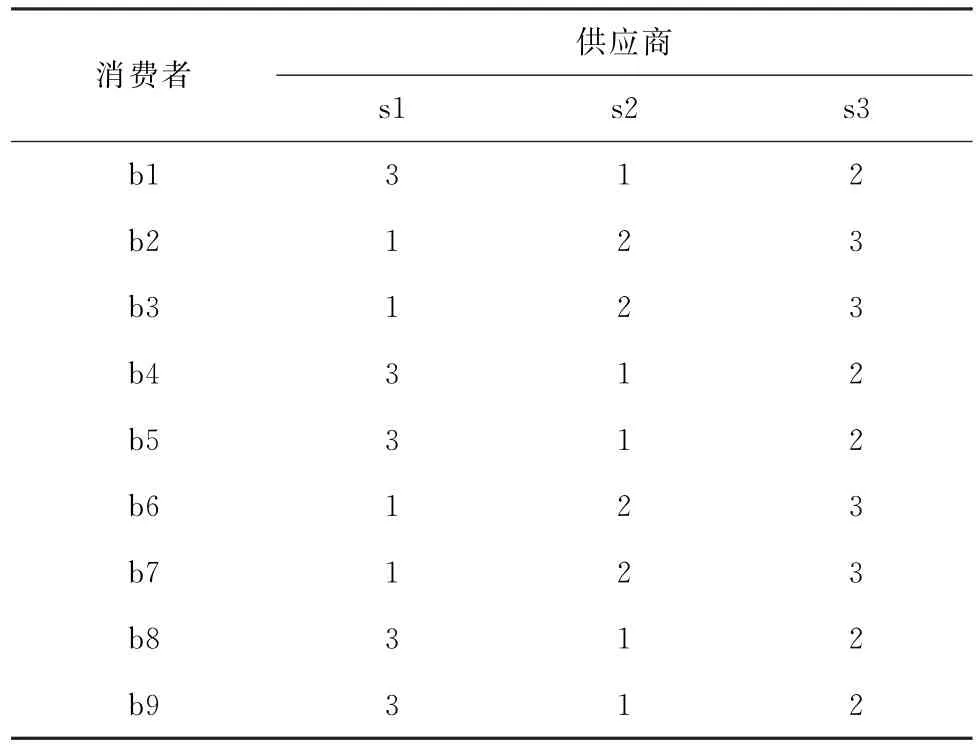
表4 消费者对供应商的满意值Tab.4 The consumers satisfaction for supplies

4.3 仿真结果

4.3.1 预处理阶段推荐算法准确性比较

在不同的邻居规模下,改进算法与经典协同过滤算法(CCF)和基于项目评分相似度填充的协同过滤(CFBRF)的EMA如图1所示。

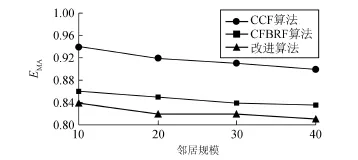
图1 3种算法EMA对比Fig.1 EMAof three algorithms

4.3.2 匹配质量比较

观察用户满意度指标,在同样的参与者、偏好相同的情况下,在第1轮匹配中匹配次数从1到9逐渐增加时,供应商和消费者的满意值如图2所示。从图2可看出,随着匹配次数的增加,消费者的满意值在增加。改进的算法相较于传统的协同过滤算法,供应商的满意值也在增加,因为算法满足消费者优先选择的情况下,由供应商按照其偏好对消费者进行筛选,最终得到匹配方案是双向选择的结果。总体来看,满意度呈上升趋势,保持双方较高的满意值,能满足双方的需求。

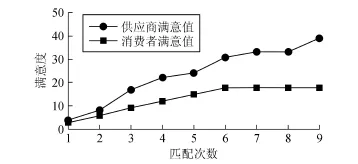
图2 供应商和消费者的满意值Fig.2 The satisfaction of supplies and consumers

比较匹配次数从1到9逐渐增加的情况下,供应商和消费者的参与度如图3所示。从图3可看出,随着匹配次数的增加,双方参与度都不断上升。

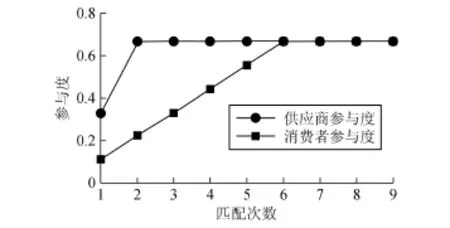
图3 供应商和消费者的参与度Fig.3 The participation of supplies and consumers

为验证算法的有效性,算法在第1轮到第5轮的供应商与消费者的参与度如图4所示。从图4可看出,在第2轮匹配中,消费者和供应商的参与度达到最高,匹配次数继续增加,在供应商参与度几乎不变的情况下,消费者的参与度会下降。由此可见,选择合适的匹配次数很重要,一味增加匹配次数不但增加内存和时间的开销,而且推荐的效果也会下降。

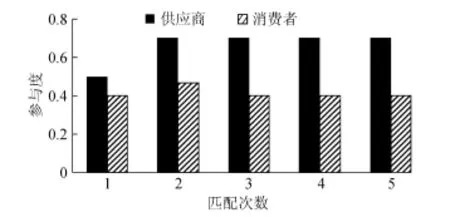
图4 第1~5轮供应商与消费者的参与度Fig.4 The participation of supplies and consumers from first to fifth matching

5 结束语

针对传统的协同过滤算法存在稀疏矩阵及忽视供应商偏好的问题,提出一种G-S框架下的推荐算法。利用改进的基于项目相似度对矩阵进行填充,能够缓解稀疏矩阵造成的问题,提高推荐准确性;G-S算法能够充分考虑到供应商和消费者双方的偏好,增加算法的稳定性。仿真结果表明,改进的算法从算法的准确性和满意值上,都能提高用户体验,有利于吸引参与者加入到电子交易平台。但是,推荐准确度还存在很大的提升空间,将社交网络的概念引入也是一个重要的方向。

[1] 杨博,赵鹏飞.推荐算法综述[J].山西大学学报:自然科学版,2011,34(3):337-350.

[2] 邓爱林,朱扬勇,施伯乐.基于项目评分预测的协同过滤推荐算法[J].软件学报,2003,14(9):1621-1628.

[3] 彭石.基于用户兴趣和项目特征的协同过滤推荐算法研究[D].长沙:中南大学,2012:14-18.

[4] Gale D,Shapley L S.College admissions and the stability of marriage[J].The American Mathematical Monthly, 1962,69(1):9-15.

[5] Shapley L S.On market games[J].Journal of Economic Theory,1969,1:9-25.

[6] Roth A E.Incentive compatibility in a market with indivisible goods[C]//Economics Letters,1982:127-132.

[7] Roth A E,Sonmez T,Utuuver M.Pairwise kidney exchange[J].Journal of Economics Theory,2005,125: 127-132.

[8] 龚亮.推荐系统实践[M].北京:人民邮电出版社,2012: 59-61.

[9] 曾赛.基于社交网络信任模型的项目推荐系统[D].广州:华南理工大学,2012:33-39.

[10] 周静.基于信任的协同过滤推荐算法研究[D].秦皇岛:燕山大学,2013:27-32.

[11] 周军锋,汤显,郭景峰.一种优化的协同过滤推荐算[J].计算机研究与发展,2004,40(10):1843-1847.

[12] 曹建新,杨宁,夏培勇.一种基于改进信息熵的协同过滤算法[J].微计算机信息,2012,40(10):181-183.

[13] 苏彦秋.SNS中意见领袖对消费者购买意向的影响研究[D].大连:东北财经大学,2013:18-19.

编辑:翁史振

A collaborative filtering algorithm on G-S model

Gu Kai1,Liu Jianming2
(1.School of Electronic Engineering and Automation,Guilin University of Electronic Technology,Guilin 541004,China; 2.School of Computer Science and Engineering,Guilin University of Electronic Technology,Guilin 541004,China)

The absence of supplies’interest and the execution efficiency of recommendation technology based on collaborative filtering algorithm is relatively low with the data sparsity,so a modified collaborative filtering algorithm is proposed.Firstly,it prefills the rating matrix by the approved algorithm and makes sure of the users’rates.Then the improved G-S algorithm for consumers and sellers provides appropriate match on both sides according to the recommended goods based on the collaborative filtering algorithm.The experimental results show that the algorithm has high execution and satisfaction.

collaborative filtering algorithm;satisfaction;Pareto principle;information entropy

TP391

A

1673-808X(2015)05-0395-06

2015-03-09

国家自然科学基金(61262074)

刘建明(1975-),男,广西桂林人,教授,博士,研究方向为计算机及通信网络组网工程。E-mail:jmliu_gl@sina.com引文格式:顾凯,刘建明.G-S模型下的协同过滤算法[J].桂林电子科技大学学报,2015,35(5):395-400.