基于信息熵特征的超宽带探地雷达快速BP成像算法

程生见,欧阳缮,廖桂生,2

基于信息熵特征的超宽带探地雷达快速BP成像算法

程生见1,欧阳缮1,廖桂生1,2

(1.桂林电子科技大学信息与通信学院,广西桂林 541004; 2.西安电子科技大学电子工程学院,西安 710071)

针对超宽带探地雷达BP成像算法计算量大、运算速度慢的缺陷,利用对折射点近似求解算法进行优化与处理,提出一种基于信息熵特征的快速BP成像算法。算法以信息熵为统计量来判定目标回波在B-scan数据列上的分布区域,利用目标区域数据参与BP成像。实测数据对比验证结果表明,优化后的BP算法运算速度快,成像精度高。

超宽带;探地雷达;BP算法;信息熵;优化

探地雷达是一种利用电磁波反射探测目标的无损探测技术,该技术在地质灾害探测、考古探测、军事探测等领域得到了广泛的应用[1-3]。超宽带脉冲体制探地雷达成像原理与SAR成像原理有相同之处,探地雷达成像可借鉴其原理。BP(back propagation)算法源自于计算机应用中断层扫描(computer tomograph,简称CT)技术,又称为后向投影算法,被广泛应用于SAR成像,其基本原理是计算成像区域中的每一个像素点到每一个天线位置之间的距离,然后将其后向散射回波在时域进行相干叠加,获得该像素点的散射强度信息,进而使回波中的目标信号聚焦,达到高分辨成像的目的。

BP算法存在运算量巨大、不利于实时处理的缺陷,这是由于计算各个像素点时延的计算量巨大,导致计算效率比较低。如何快速实现BP算法成像是合成孔径雷达方向的研究热点,国内外专家学者提出了相应的快速实现方法。Boag等[4]提出了一种快速BP算法,其原理是将成像区域分块划分,通过分级相干累加的方式减小BP算法的运算量,然而该算法虽然降低了一定的算法运算量,但难以满足现阶段实时成像的需求。王宏等[5]基于脉冲成像的特点提出了一种改进的快速后向投影成像(fast back propagation,简称FBP)算法,与BP算法相比,其在运算速度上有一定提高,但成像精度有所下降。周琳等[6]提出一种互相关投影成像(cross-correlated back projection,简称CBP)算法,该算法充分利用已获取回波之间的相关性,在成像时进行互相关处理,最终获得像素点聚焦成像结果,成像精度有一定提升,但其运算复杂度仍较高,运算时间比BP算法成像长。探地雷达BP成像时延求解算法的改进是降低BP成像时间的另一种有效方法。基于实际的工程应用,Johansson等[7]提出一种折射点近似估计求解算法,它将复杂的四次方程求解过程转化为一次方程的求解,大大地降低了运算时间。继而,蔚建斌等[8]提出了一种改进的计算方法,使近似求解运算更符合电磁波实际折射过程,并获得更精确的近似值。Zhou等[9]考虑到工程应用近似算法在天线远离目标足够远时的非收敛性,对原有算法进行优化,优化后的算法具有较高精度。

上述优化算法的主要特点如下:1)从理论上减少算法的变量乘法或除法的运算量,进而改进算法结构来优化算法;2)对成像区域进行分割,减少回波投影数量,进而降低运算量。基于此,通过优化与处理折射点近似求解算法,基于信息熵特征对BP成像算法进行改进。

1 探地雷达BP成像原理

探地雷达在探测地表下的目标体时,由于上表面不均匀或存在障碍物,为保证天线的水平移动,通常采用离地探测的方法。x轴将场景分为2个部分:一部分为空气,近似作为自由空间分析,其磁导率为μ0,介电常数为ε0;另一部分为均匀的介质,其介电常数为ε1,介质的相对介电常数为εr,且εr＞1。磁导率在大多数实际应用中保持不变,即μ1=μ0。第i个发射天线的电磁波入射到地面后,在(xr,0)处发生折射,折射波到达目标体后发生反射,接收天线接收回波信号。实际测量中,发射天线与接收天线相隔很近,为便于分析,将双程时延近似为入射时延的2倍,将成像区域划分为N×M个像素点,以任一像素点O为例。探地雷达成像场景如图1所示。

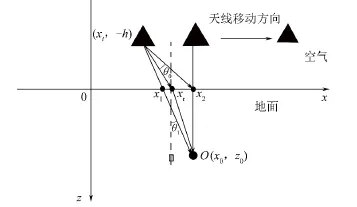
图1 探地雷达成像场景Fig.1 The imaging scene of GPR

电磁波在上表面发生折射后,入射波与折射波的关系满足Snell折射定律:

由三角形基本定理推得:

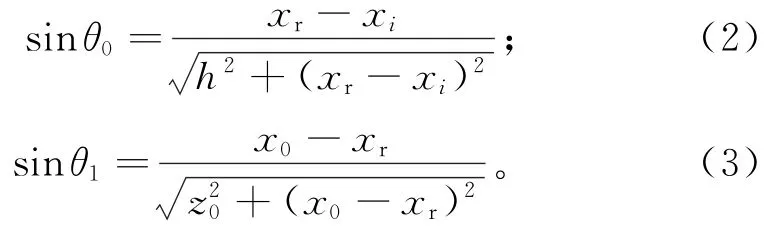
将式(2)、(3)代入式(1),得到方程:

该方程是关于折射点横坐标xr的一元四次方程。由于四次以上代数方程无直接的开方运算求根方法,通常运用数值方法(如牛顿迭代法、二分法等)求折射点xr的位置。

求解得到xr的值后,第i个天线测得的回波在O点的双程时延为:

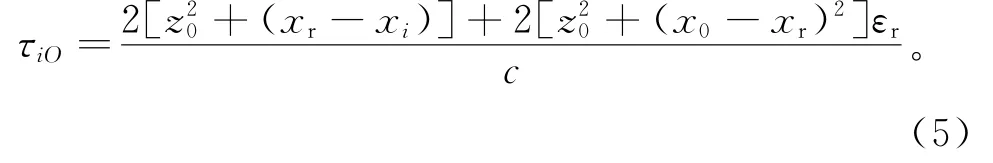
根据式(4)、(5)求出成像区域像素点O在所有A-scan数据上幅度的相干叠加,得到目标的后向散射强度。重复上述的步骤,即可求出所有像素点的聚焦结果。可以看出,探地雷达BP算法的时延主要由两部分时延的计算量、相干叠加的计算量构成。探地雷达反射点的求解涉及四元方程,导致求解运算量比较大。此时,有用的数据是目标的反射信号,而实际应用中,探地雷达回波数据中目标信号只占很小一部分,利用少数的目标区域回波信号进行成像运算,将很大程度提高成像算法处理速度。

2 探地雷达介质中折射点计算优化方法

其中:x1为上下两部分场景的相对介电常数为1时,电磁波在介质中沿直线传播与两部分分界面的交点; x2为相对介电常数为无穷大时,折射角为0时折射点的位置。x1、x2为2种理想的折射点位置。

要使计算结果更接近折射点的精确值,有必要考虑电磁波的实际传播。实际探测时,由于探地雷达离地探测,雷达的入射角比较小。蔚建斌等[8]提出的改进方法为:

2.1 折射点计算方法

为减少迭代次数,降低运算量,Johansson等[7]提出一种折射点近似求解算法,它将折射点求解过程的复杂四次方程转化为一次方程运算,大幅度减少了运算时间。

根据图1,折射点的近似值

根据图1,其结构关系为:

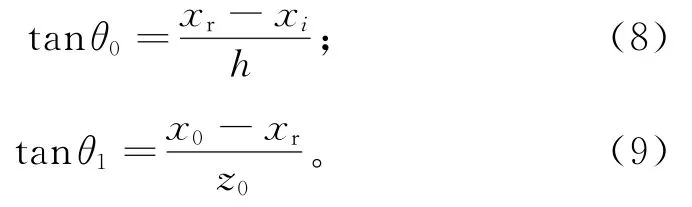
将式(7)代入式(4)求得折射点:

设探地雷达探测场景为3 m×1 m,探地雷达离地探测,离地0.2 m。地下介质与空气的相对介电常数为3,目标O点所在坐标为(0,0.3)。天线移动位置从z轴开始水平移动,每次移动0.04 m。折射点计算场景如图2所示。

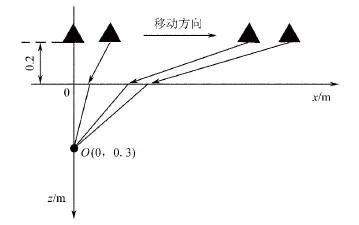
图2 折射点计算的场景Fig.2 The scene of refraction point calculation

分析可知,蔚建斌等[8]提出的改进算法与工程上的近似算法都是线性递增的,当天线远离目标位置时,它们的折射点近似误差越来越大,这对于后续精确信号的处理产生很大的干扰。对于工程上电磁波折射点近似方法的计算误差急剧增大问题,Zhou等[9]提出一种针对工程折射点近处计算的改进方法。实际计算中,当天线位置远离目标移动时,折射点xr位置存在一个极限,利用这个极限位置重新构造折射点的近似函数,可达到改进算法的目的。针对天线靠近目标位置的探测,蔚建斌等[8]提出的算法求解更合理,利用该算法与上述思想结合,可获得更好的近似效果。

目标折射点位置随天线的移动逐渐趋向平稳。当天线移向无穷远时,即|xi-x0|≪+∞,此时,式(4)可化简为:

解得:

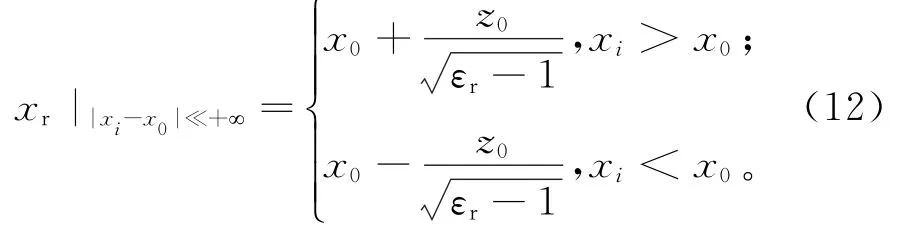
所求得的xr为折射点位置的一个极限值,当天线距离目标到达一个临界点后,折射点的求解位置不再随天线移动而变化。控制近似求解的范围,可降低误差的产生。联立式(10)、(12),即可求出需要改进的近似函数范围端点。根据天线移动的对称性,在O点左右天线对称位置各自存在一个交点:

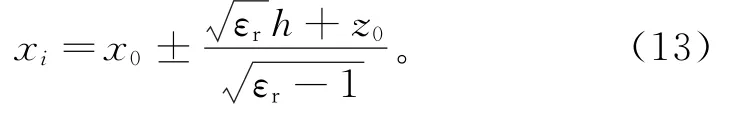
利用式(13),提出一种折射近似算法,当天线位置大于xi时,折射点为固定值。所提出的折射估计函数为:

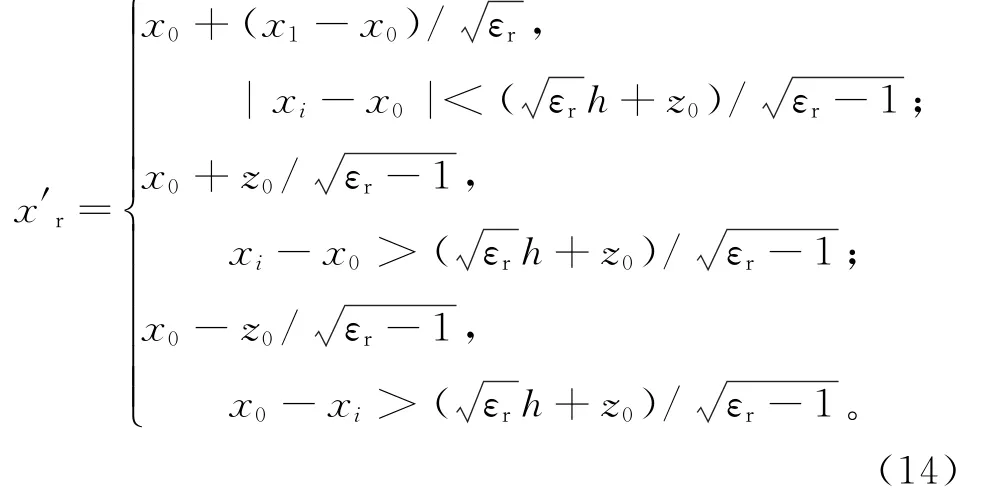
2.2 算法理论分析

采用图2所示的模拟场景,分别采用本研究提出的改进算法、文献[9]的优化算法与工程算法进行折射点位置计算,计算结果和误差对比如图3所示。从图3可看出,采用本算法估计的折射点更接近于真实值,近似的折射点不再随距离增加而增加,在天线位置大于xi后折射点位置保持平稳状态,更符合实际电磁波的折射特性。改进算法将复杂的一元多次方程求解过程近似为一个一次多项式的计算,大大地降低了算法复杂度。

图3 各算法折射点计算结果Fig.3 The refraction point calculation results of each algorithm

3 基于信息熵特征的快速BP成像

3.1 理论分析与算法流程

BP算法的成像过程实质上是求时延,然后根据时延求其幅度进行叠加的过程,它主要是将目标的双曲线回波信号进行累加。然而,在实际的探地雷达应用环境中,探测到目标存在的回波数据只占少部分,而BP算法要求将所有的回波数据进行叠加处理。可见,众多无目标信号幅度的叠加过程是多余的,它大大增加了BP算法的计算量,使其处理速度变慢。准确判断目标信号的反射回波在接收的B-scan数据中的分布状况后,BP聚焦成像时,只利用目标回波数据进行运算,即可实现快速成像。

信息熵[10-11]利用数值形式表达一个随机变量取值的不确定性程度,表示变量信息含量的多少。本研究将信息熵的概念引入探地雷达回波信号处理中,算法步骤为:

1)由于直达波等强干扰信号的存在,各列的目标信号存在与否所引起的信息熵变化不大,因此,需要对接收到的原始回波信号进行杂波抑制处理,此处采用均值法进行处理。

2)对处理后的数据~x,求测线方向上每一个测点的信息熵:

4)将步骤3)所确定的目标信号区域进行BP成像,由于非目标信号区域并未参与叠加与时延求取运算,这大大减少了成像时的运算量,实现了BP算法的优化。

3.2 实测数据处理和分析

利用脉冲信号发生器、低噪声放大器、喇叭天线、安捷伦示波器等工具,设置沙坑为测试背景。沙坑中埋有一个拱形的铁片,埋深0.05 m,铁片圆面的半径为0.265 m,弦长0.4 m,收发分置天线间距0.355 m,离地0.1 m,天线的长度0.18 m,天线每次移动步长0.02 m,总计采集40组A-scan数据。分别用BP算法、改进算法与CBP算法在同一台电脑上运用Matlab实现成像。使用均值将各种成像算法所得图像杂波去除后,原始回波图像及成像效果分别如图4 ~7所示。各算法运行时间如表1所示。

图4 原始回波图像Fig.4 Original echo image

图5 BP算法成像Fig.5 BP algorithm imaging

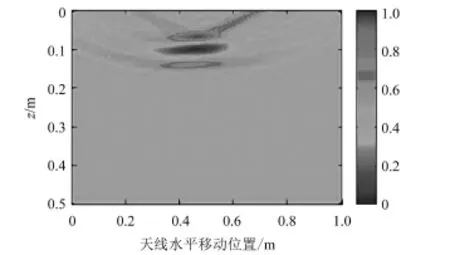
图6 改进的BP算法成像Fig.6 The improved BP algorithm imaging

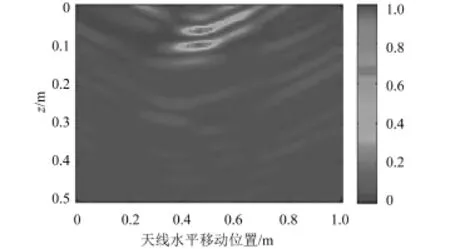
图7 CBP算法成像Fig.7 CBP algorithm imaging

表1 各种算法成像处理时间Tab.1 The processing time of various algorithms

从图4~7和表1可看出,改进算法聚焦成像效果比传统BP算法聚焦效果好,旁瓣干扰少。与CBP成像算法效果相比,虽然聚焦效果略有不足,但从各算法成像处理时间上看,改进算法时间仅为4.1 s,较BP成像算法的38.5 s和CBP算法38.8 s,成像速度得到大大地提升,表明改进算法具有较好的有效性和实用性。

4 结束语

针对BP算法成像时间长、成像分辨率低的不足,分析理论GPR成像领域的一个通用问题:分层介质中的电磁波双程时延计算,进而提出电磁波折射点坐标近似求解方法。实验分析结果表明,所提出的优化方法优化了折射点的估计精度,提高了计算效率,进而降低了BP成像的运算时间。这种优化方法是基于电磁波的折射定律推导得到的,具有较强的通用性,在任何涉及电磁波在分层介质中传播的时延求解的应用场合均可发挥很好的作用。在此基础上,以信息熵为统计量,判断目标回波在整个B-scan回波数据中的分布,在BP成像时,只是目标回波数据参与运算与聚焦,以降低运算时间,实现快速的BP成像,实现了BP成像算法的有效改进。改进算法大大地降低了运算时间,基本达到BP实时成像的目的。

[1] Nishimoto M,Yoshida D.Signal processing for extraction of target response from distorted GPR data[C]// Proceedings of 2013 URSI International Symposium on-Electromagnetic Theory(EMTS),2013:1109-1112.

[2] Scheers B.Ultra-wideband ground penetrating radar, with application to the detection of anti-personnel landmines[D].Brussels,Belgium:University Catholique De Louvain,2001:356-362.

[3] Takahashi K,Preetz H,Igel J,et al.Influence of heterogeneous soils and clutter on the performance of groundpenetrating radar for landmine detection[J].IEEE Transactions on Geosciences and Remote Sensing,2014, 52(6):3464-3472.

[4] Boag A,Bresler Y,Michielssen E.A multilevel domain decomposition algorithm for fast O(N 2 log N)reprojection of tomographic images[J].IEEE Transactions on Image Processing,2000,9(9):1573-1582.

[5] 王宏,周正欧,李廷军,等.超宽带脉冲穿墙雷达互相关BP成像[J].电子科技大学学报,2011,40(1):16-19.

[6] 周琳,粟毅.基于互相关的探地雷达反向投影成像算法[J].电子与信息学报,2011,33(11):2714-2719.

[7] Johansson E M,Mast J E.Three-dimensional groundpenetrating radar imaging using synthetic aperture timedomain focusing[C]//SPIE's 1994 International Symposium on Optics,Imaging,and Instrumentation.International Society for Optics and Photonics,1994:205-214.

[8] 蔚建斌,陈自力,江涛.探地雷达在地下介质中传播路径的计算[J].电波科学学报,2009,24(5):925-928.

[9] Zhou L,Huang C,Su Y.A fast back-projection algorithm based on cross correlation for GPR imaging[J]. IEEE Geoscience and Remote Sensing Letters,2012,9 (2):228-232.

[10] 申家全,闫怀志,胡昌振.基于图像熵的探地雷达杂波抑制效果评价[J].电波科学学报,2011,26(2):267-271.

[11] Solimene R,Cuccaro A,Dell'Aversano A,et al.Ground clutter removal in GPR surveys[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2014,7(3):792-798.

编辑:黎仁惠

A fast back-projection imaging algorithm based on entropy feature for ultra-wideband GPR

Cheng Shengjian1,Ouyang Shan1,Liao Guisheng1,2
(1.School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin 541004,China; 2.School of Electronic Engineering,Xidian University,Xi’an 710071,China)

BP algorithm is widely used in ultra-wideband ground penetrating radar imaging,but it has a drawback with large computation and lower speed.In this paper,through optimizing and processing refraction point approximation algorithm, the rapid BP imaging algorithm based on information entropy characteristics is presented,which determines the target echo in B-scan data columns distribution area by information entropy statistics with the region data participating in BP imaging data.The experimental result shows that the optimized BP algorithm computes fast and the image precision is high.

ultra-wideband;ground penetration radar;BP algorithm;entropy;optimization

TN957.52;P631

A

1673-808X(2015)05-0345-05

2015-03-19

国家自然科学基金(61371186);广西自然科学基金(2013GXNSFFA019004)

欧阳缮(1960-),男,江西安福人,教授,博士,研究方向为通信和雷达信号处理、自适应滤波理论和应用。E-mail:hmoysh@guet.edu.cn引文格式:程生见,欧阳缮,廖桂生.基于信息熵特征的超宽带探地雷达快速BP成像算法[J].桂林电子科技大学学报,2015,35(5):345-349.