空时频域中欠定混合条件下的波达方向估计*

朱立为，汪亚，王翔，黄知涛(.国防科技大学电子科学与工程学院，湖南长沙40073；.电子信息系统复杂电磁环境效应国家重点实验室，河南洛阳47003)

空时频域中欠定混合条件下的波达方向估计*

朱立为1，2，汪亚1，王翔2，黄知涛2
(1.国防科技大学电子科学与工程学院，湖南长沙410073；
2.电子信息系统复杂电磁环境效应国家重点实验室，河南洛阳471003)

波达方向估计是阵列信号处理领域的热点问题，但经典的波达方向估计方法通常要求阵元数大于源信号个数，即满足超定条件，而在实际中往往面临的是源信号个数大于阵元数的欠定条件。基于此，提出了一种基于空间时频分布的多重信号分类扩展算法，通过将空间时频分布矩阵进行扩展，实现了欠定条件下的波达方向估计。相比时频多重信号分类算法，所提算法能同时适应超定和欠定条件；相比已有的欠定波达方向估计方法，其不但保证了波达方向估计的精度，而且放宽了对源信号稀疏性的要求，同时还降低了对快拍数的要求。仿真实验结果证明了该方法的有效性。

波达方向；时频分布；欠定

在阵列信号处理领域，波达方向(Direction Of Arrival，DOA)估计是声呐、雷达、地震学的一个重要研究课题。传统的DOA估计方法，如多重信号分类(MUltiple SIgnal Classification，MUSIC)方法［1］、改进MUSIC方法［2-3］、时频MUSIC方法［4］、极大似然方法［5］、空间谱估计方法［6］、波束成形方法［7］等，一般要求信号环境满足超定条件，即接收天线的阵元个数要大于潜在的源信号个数。但在实际的信号环境下，这一条件并不总能满足。例如，在机载或星载的非合作通信应用中，由于地面雷达、通信等各种辐射源的大量使用，并且使用的频段不断扩展、相互重叠，加上各种自然辐射产生的无意干扰，使得机载或星载接收设备面临时域高度密集、频域严重混叠、空间相互交错的复杂电磁环境，而实际上机载或星载设备本身受体积限制，阵元数不能随意增加，且阵元数目越多，接收设备结构越复杂，价格也越昂贵。因此需要利用有限的接收阵元对尽可能多的源信号的DOA进行估计，即需要研究可以适用于欠定混合条件下的DOA估计方法。

近年来，相继出现了一些适应欠定混合条件的DOA估计算法。主要可分为两类:一是基于高阶累积量的欠定DOA估计算法［8-9］。文献［9］利用四阶累积量代替协方差矩阵，将MUSIC算法扩展成4-MUSIC算法(4-MUSIC)。为了进一步提高阵列对多个潜在源信号的DOA估计能力，文献［10］将四阶累积量推广到任意偶数阶累积量，提出了2q-MUSIC(q＞1)算法，并详细分析了采用不同阵列结构等价的虚拟阵元数目。虽然这些高阶累积量算法可以通过扩展产生虚拟的阵元以适应欠定混合条件，但是高阶累积量的计算过程复杂且需要较多的样本数目才能保证算法的估计精度。二是其他一些基于时频域稀疏性的DOA估计算法，如退化分解估计技术(Degenerate Unmixing Estimation Technique，DUET)等也能适应欠定混合条件［11-15］，但这些方法对信号的时频域稀疏性要求过于严格，即任意时频点只有一个源信号起主导作用，其余源信号取值为0［16］，这在实际应用中并不能完全满足。

本文提出了基于空间时频分布(Spatial Time-Frequency Distributions，STFD)的MUSIC算法(STFD-MUSIC)，通过扩展空间时频混合矩阵［17］来实现欠定条件下的DOA估计。该方法并不需要假设信号是稀疏的，且能够降低算法对快拍数的要求。

1 算法分析

假设N个窄带远场信号S(t)=［s1(t)，…，sN(t)］T入射到由M个阵元组成的天线阵上，观测信号可以写为:

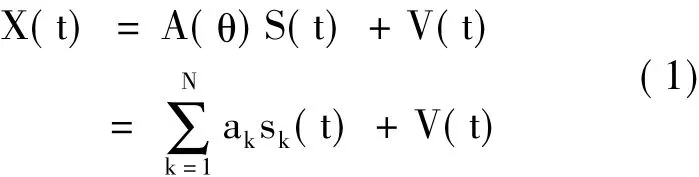
其中，X(t)=［x1(t)，…，xM(t)］T和V(t)=［v1(t)，…，vM(t)］T分别表示M个阵元的输出即观测信号和噪声，θ=［θ1，…，θN］代表各源信号的入射角度，混合矩阵A(θ)=［a1(θ1)，…，aN(θN)］表示传输矩阵，作为线性矩阵，其K列可以表示为:

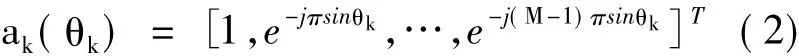
本文研究的欠定条件指的是阵元数小于源信号数目，即N＞M；研究目的是估计θ。

1.1 空间时频分布基本理论

本文算法的核心思路是利用观测信号的空间时频分布矩阵实现阵列的虚拟扩展，实现欠定混合条件下的DOA估计。

空间时频分布矩阵定义如式(3)、式(4):

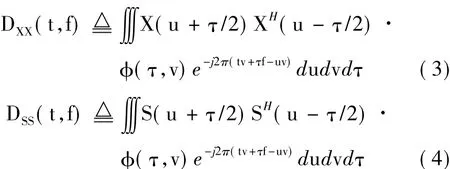
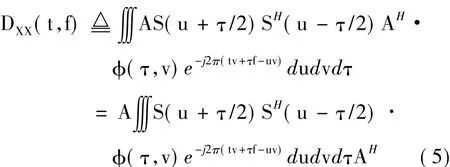
联立式(4)和式(5)，可得接收信号的空间时频分布矩阵与源信号的空间时频分布矩阵之间的关系，其表示如式(6):

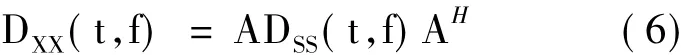
由文献［18］易知，接收信号的空间时频分布矩阵的对角元素称为自源点(auto-terms)，也称自项，其对应着X(t)中代表各个信号的向量平方；而反对角元素称为互源点(cross-terms)，对应着多个信号向量的线性组合。

1.2 算法假设条件

为了能够在时频域上估计出源信号的DOA，采用了Wigner-Vill分布。同时，假设源信号满足以下条件:

假设1:在时频平面上信号的自源时频点与互源时频点几乎是不混叠的；

根据假设2可知本文算法在天线阵元数一定时可接收处理的最大源信号个数。

1.3 算法描述

1.3.1 自源点选择

对于任意自源点(t，f)∈Ωs(Ω表示整个时频平面)，接收信号X(t)的空间时频分布矩阵可以表示为:

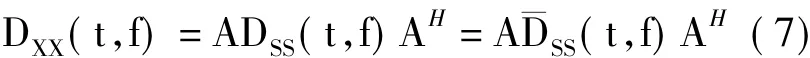
式中，D¯SS(t，f)表示对角矩阵，其表示为D¯SS(t，f)=diag［Ds1s1(t，f)，…，DsNsN(t，f)］。

先找出自源点，同时抑制互源点，则可以实现对各个源信号的DOA估计。利用的准则如式(8)所示:

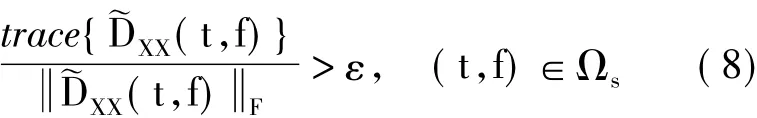
在超定混合条件下，直接对DXX(t，f)进行奇异值分解可以很容易地估计出源信号的DOA。但在欠定混合条件下，不能直接分解来估计源信号的DOA。下面将介绍一种能适用于欠定混合条件下基于空间时频分布的DOA估计算法。1.3.2基于空间时频分布的扩展矩阵构造

根据式(8)所述的准则，求出自源点的个数，设在式(8)准则下找出K个自源点，则K个自源点对应的时频分布矩阵表示如式(9)所示:

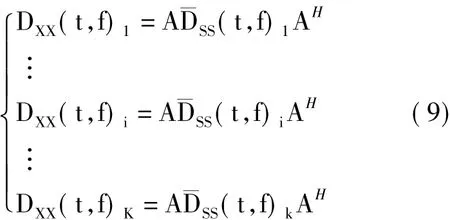
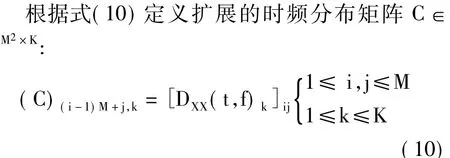
定义矩阵D∈K×M，其中(D)km=(Dk)mm(k =1，…，K，m=1，…，M)，则C可以表示成如式(11)所示的形式:

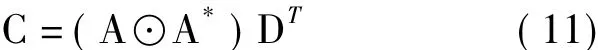
式中，A⊙A*=［a1θ1)，…，aN(θN)⊗θN)］，其中*，⊙和⊗分别表示复数的转置、ri-Rao乘积和Kronecker乘积。因此，要解决的问题就是当N＞M时，如何利用矩阵C来估计角度θ。

一般来说，假设N≤min(M2，K)。根据文献［19］中的证明可知，当潜在源信号个数与阵元数满足假设2的关系式时，则A⊙A*和D是列满秩的。而A⊙A*和D是列满秩的，意味着C也是列满秩的，并且C的秩就等于源信号个数N。

1.3.3 子空间求解与角度估计

与传统的MUSIC方法类似，可以直接对自相关阵RC=CCH进行奇异值分解来获得噪声子空间。在本文算法中，虽然信号子空间和噪声子空间可以通过任意一个RCi进行奇异值分解求得，但是当RCi奇异性较强时，子空间的估计精度会很差，进而影响DOA的估计结果。因此，提出对扩展自相关矩阵集合{RCi|i=1，…，K}进行联合对角化的方法求解信号子空间和噪声子空间。相比单一矩阵的处理方法，利用多个矩阵的估计方法可以同时保证算法的估计精度和信噪比适应能力。采用联合对角化的方法分解自相关阵RC= CCH，其分解后的主要形式如式(12):

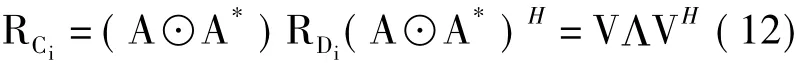
式中，RDi=(，Λ为×对角阵。Λ的N个较大对角对应着信号子空间，M2-N个较小对角线元素代表着噪声子空间。因此，可以利用V矩阵相应的M2-N列向量构成的噪声子空间来估计源信号的DOA。根据文献［20］中的研究，可以使用式(13)所示的代价函数进行联合对角化。

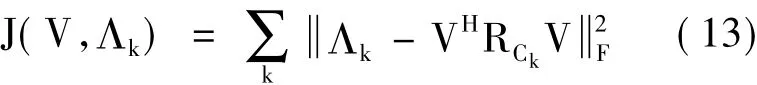
当式(13)的值最小时，可以估计出信号子空间与噪声子空间。因为RCi是Hermitian阵，所以RCi中组成信号子空间的列向量与组成噪声子空间的列向量是正交的。详细来说，Span{VS}= Span{Α⊙Α*}，其中VS是N维信号子空间的基，则Α⊙Α*中所有列向量都与VN中的列向量正交，而且是M2-N维噪声子空间的基。因此，所有{ai(θi)(θi)，1≤i≤N}向量都与VN中的列向量正交，因此有式(14)所示的关系式:

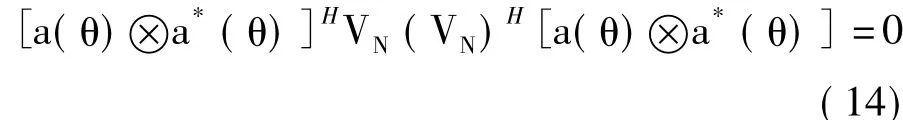
在实际运用过程中，常常定义空间伪谱的概念来运用上述正交性进行DOA估计，如式(15):

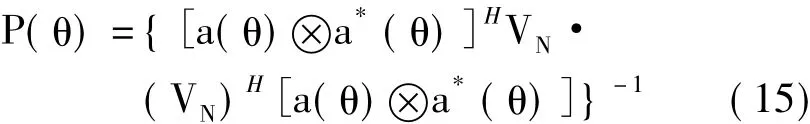
从式(15)可知，只要找出最大“谱线”P(θ)的位置处对应的角度，则这个角度就等于要估计的某一源信号的DOA。

综上所述，本文所提出的基于空间时频分布的欠定混合条件下DOA估计的核心算法步骤如下:

(i-1)M+j，k)ij计算拓维后的新矩阵，同时求出C^的协方差矩阵=，然后对协方差矩阵进行联合对角化，估计出VN。

2 仿真分析

2.1 评价准则

为了验证算法的性能，仿真时采用平均测向均方根误差作为指标来衡量DOA的估计性能，定义平均测向均方根误差(Root-Mean-Square Error，RMSE):

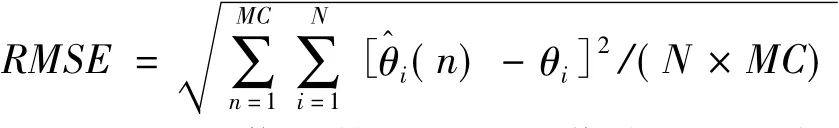
2.2 仿真实验

仿真分析中，用4个线性调频信号作为源信号，其频率分别为:1000MHz，1000.1MHz，1000.4MHz，1000.5MHz，码速率都为200kbit/s，角度分别为:-43°，-13°，26°，48°。仿真实验1到4中接收天线是阵元数目为3的均匀线阵，仿真实验5中接收天线是阵元数目分别为4和5的均匀线阵，相邻阵元间距为半波长。为降低采样率和计算量，先将射频信号的频率变到中频，中频频率分别为350kHz，450kHz，750kHz和850kHz，采样率为2MHz。仿真将［-90°，90°］的空域以0.1°间隔均匀采样，得到离散的假设角度集θ～，进行500次蒙特卡洛试验。

在仿真实验中，对本文算法与4-MUSIC算法进行了性能比较，而没有将本文算法与基于时频稀疏性的DOA估计算法进行比较，这是因为实验设置的源信号在时频域是重叠的，不满足时频域稀疏性，基于稀疏性的DOA估计算法无法完成源信号DOA的估计。

在图1中，仿真实验给出了信噪比(Signal to Noise Ratio，SNR)为10dB，采样点数分别为1024和512时，本文算法与4-MUSIC算法的任意10次仿真实验的空域伪谱估计结果。从图1(a)可以看出本文算法的空间谱中出现了4个显著的谱峰，能够清晰地分辨出四个源信号的DOA；图1(b)是4-MUSIC算法的空间谱，图中出现了4个大致的谱峰，勉强能分辨出四个源信号的DOA。当采样点数降低时，从图1(c)中可以看出，本文算法仍然可以清晰地分辨出源信号的DOA；而图1(d)中4-MUSIC算法的空间谱上的谱峰已很不明显，难以分辨出源信号的DOA。

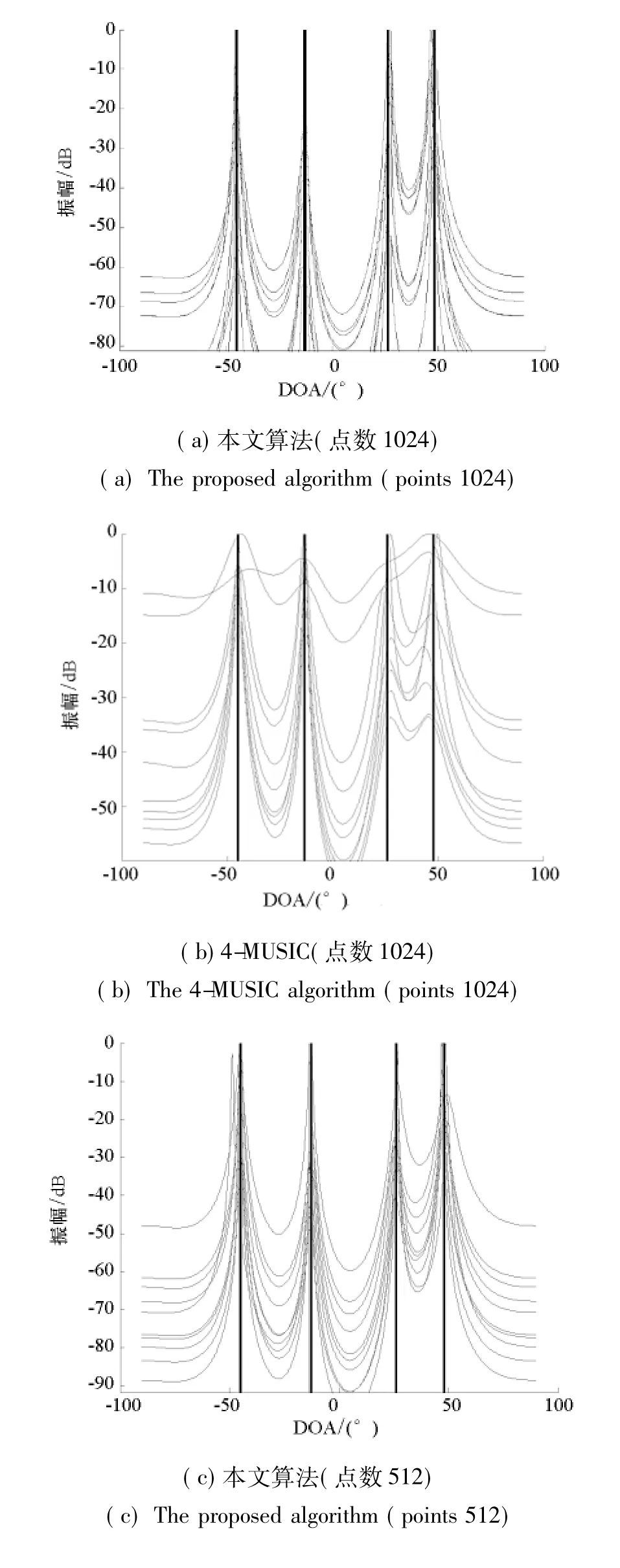
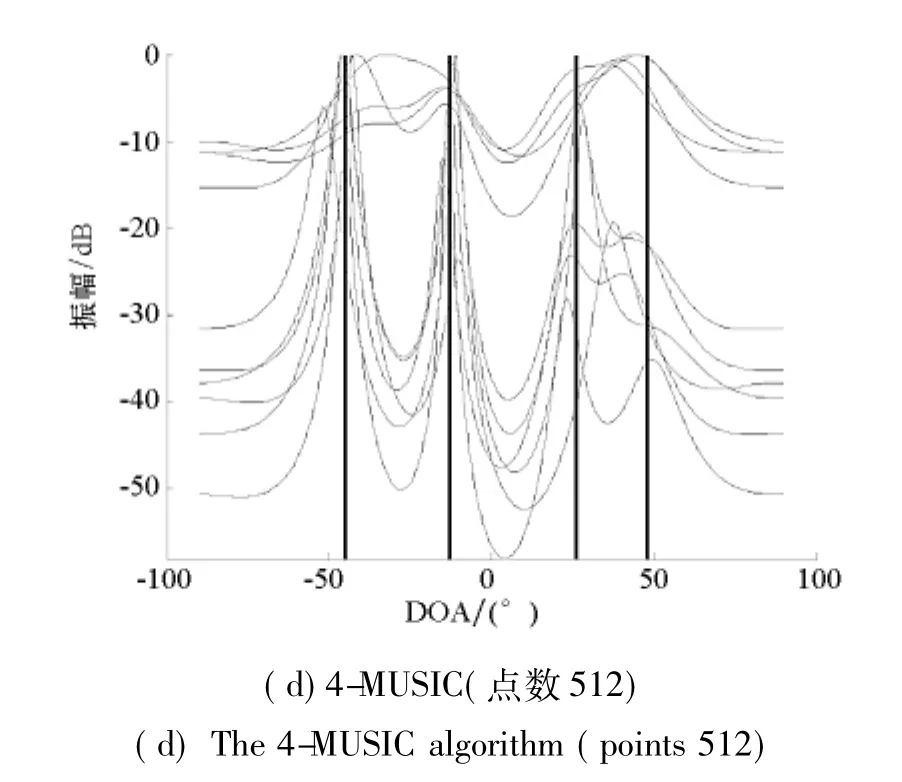
图1本文算法与4-MUSIC算法空间伪谱Fig.1 Spatial pseudo-spectrums of the proposed and 4-MUSIC algorithm

图2 为信噪比为10dB时，本文算法与4-MUSIC算法的平均测向均方根误差RMSE随采样点数变化的曲线(图中CRLB为克拉美罗下限)。从图中可看出，随着采样点数的增加，平均测向均方根误差随之减少；在相同的采样点数条件下，本文算法的平均测向均方根误差更小，DOA估计精度更高；而在相同的DOA估计精度下，本文算法需要采样点数要少，因为在相同的估计性能条件下，相比4-MUSIC的高阶累积量的估计，本文算法的空间时频分布矩阵估计需要的采样数据更少。

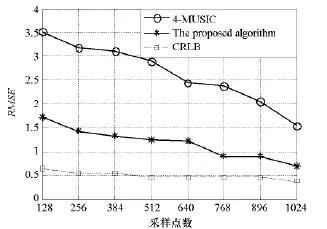
图2不同采样点数的RMSE估计结果Fig.2 Estimation results of RMSE for different sample points

图3 为采样点数等于1024、信噪比从-5dB到30dB变化时，本文算法与4-MUSIC算法的平均测向均方根误差RMSE随信噪比变化曲线。从图中可以看出，随着信噪比的变化，本文算法的平均测向均方根误差更接近CRLB，DOA估计精度更高。当DOA估计精度相同时，本文算法比4-MUSIC算法适应的信噪比更低。

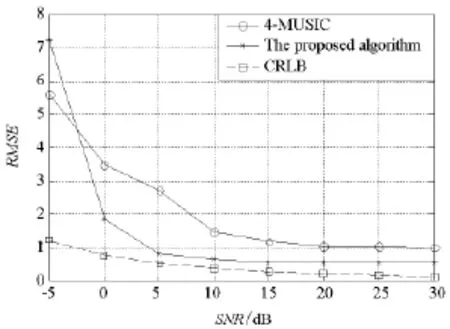
图3 不同的SNR的估计结果(欠定条件)Fig.3 Estimation results of RMSE for different SNR(underdetermined)

假设阵列误差矢量ei(1≤i≤2)是相互独立的高斯随机变量，即满足E{eieHj}=σ2δIN，令σ2= 0.000 3，图4给出了本文算法和4-MUSIC算法的平均测向均方根误差RMSE随信噪比变化的曲线。从图中可以看出，相比4-MUSIC算法，本文算法的阵列误差适应能力更强。

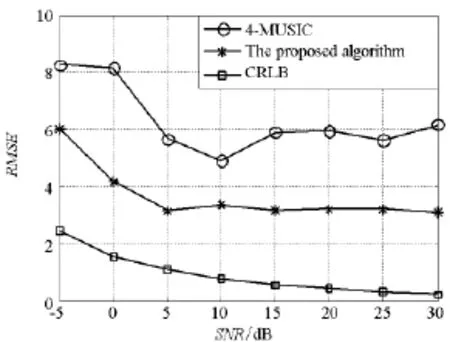
图4不同的SNR的估计结果(考虑阵列误差)Fig.4 Estimation results of RMSE for different SNR(model error)

图5 为采样点数设为1024，信噪比从-5dB到30dB变化，阵元数分别为5和6时，本文算法与4-MUSIC算法的平均测向均方根误差RMSE随信噪比变化曲线。结合图3的结果可以看出，本文的DOA估计算法可以有效应用于适定和超定的接收条件，极大地扩展了算法的实际应用范围，并且随着阵元数的增加，DOA估计性能也随之提高。

3 结论

针对欠定混合条件下DOA估计问题，提出了一种基于空间时频域的估计算法。该方法通过Khatri-Rao乘积和Kronecker乘积对空间时频混合矩阵进行扩展，以适应欠定混合条件。提出的欠定DOA估计算法中，采用联合对角化的方法来处理空间时频矩阵，增强了算法的稳健性，提高了算法在低信噪比条件下的DOA估计能力。仿真结果表明，所提算法的DOA估计性能优于4-MUSIC算法。同时，随着天线阵元数的增加，所提算法对DOA的估计性能还会大幅度提升。

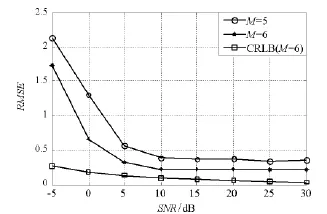
图5 不同的SNR的估计结果(接收阵元为5，6)Fig.5 Estimation results of RMSE for different SNR(5 and 6 array elements)

References)

［1］Schmidt R O.Multiple emitter location and signal parameter estimation［J］.IEEE Transactions on Antennas and Propagation，1986，34(3):276-280.

［2］Zhou Q C，Gao H T，Wang F，etal.Modified DOA estimation methods with unknown source number based on projection pretransformation［J］.Progress in Electromagnetics Research B，2012，38:387-403.

［3］Zhou Q C，Gao H T，Wang F.A high resolution DOA estimatingmethod without estimating the number of sources［J］.Progress in Electromagnetics Research C，2012，25:233-247.

［4］Belouchrani A，Amin M G.Time-frequency MUSIC［J］.IEEE Signal Processing，Letters，1999，6(5):109-110.

［5］Ziskind I，Wax M.Maximum likelihood localization of multiple sources by alternating projection［J］.IEEE Transactions on Acoustics Speech＆Signal Processing，1988，36(10):1553-1560.

［6］Malioutov D，Cetin M，Willsky A S.A sparse signal reconstruction perspective for source localization with sensor arrays［J］.IEEE Transactions on Signal Processing，2005，53(8):3010-3022.

［7］Li J，Stoica P.Robust adaptive beamforming［J］.Series in Telecommunications＆Signal Processing，2006，15(7): 2345-2348.

［8］Chevalier P，Albera L，Ferréol A，et al.On the virtual array concept for higher order array processing［J］.IEEE Transactions on Signal Processing，2005，53(4):1254-1271.

［9］Porat B，Friedlander B.Direction finding algorithms based on high-order statistics［J］.IEEE Transactions on Signal Processing，1991，39(9):2016-2024.

［10］Chevalier P，Ferreol A，Albera L.High-resolution direction finding from higher order statistics:the 2-MUSIC algorithm［J］.IEEE Transactions on Signal Processing，2006，54(8):2986 -2997.

［11］Rickard S，Dietrich F.DOA estimation of many W-disjoint orthogonal sources from two mixtures using DUET［C］// Proceedings of the Tenth IEEEWorkshop on Statistical Signal and Array Processing，IEEE，2000:311-314.

［12］Araki S，Sawada H，Mukai R，et al.DOA estimation for multiple sparse sources with normalized observation vector clustering［C］//Proceedings of 2006 IEEE International Conference on Acoustics，Speech and Signal Processing，ICASSP 2006，IEEE，2006.

［13］Zhang W Y，Rao B D.A twomicrophone-based approach for source localization of multiple speech sources［J］.IEEE Transactions on Audio Speech＆Language Processing，2010，18(8):1913-1928.

［14］Zhou Z，Lu S J，Zhang E Y，et al.Underdetermined DOA estimation of LFM signals［C］//Proceedings of 2012 Second International Conference on Instrumentation，Measurement，Computer，Communication and Control(IMCCC)，IEEE，2012:869-872.

［15］Lie JP，Ng B P，See C M S.Multiple UWB emitters DOA estimation employing time hopping spread spectrum［J］.Progress in Electromagnetics Research，2008，78:83-101.

［16］王翔，黄知涛，任啸天，等.基于时频单源点检测和聚类验证技术的欠定混合盲辨识算法［J］.国防科技大学学报，2013，35(2):69-74.WANG Xiang，HUANG Zhitao，REN Xiaotian，et al.Blind identification of underdetermined mixtures based on detection of time frequency single source point and cluster validation technique［J］.Journal of National University of Defense Technology，2013，35(2):69-74.(in Chinese)

［17］Lu F B，Huang Z T，Jiang W L.Underdetermined blind separation of non-disjoint signals in time-frequency domain based onmatrix diagonalization［J］.Signal Processing，2011，91(7):1568-1577.

［18］Belouchrani A，Amin M G，Thirion-Moreau N，et al.Source separation and localization using time-frequency distributions: an overview［J］.IEEE Signal Processing Magazine，2013，30(6):97-107.

［19］De Lathauwer L.A link between the canonical decomposition in multilinear algebra and simultaneousmatrix diagonalization［J］.Siam Journal on Matrix Analysis and Applications，2006，28 (3):642-666.

［20］Golub G H，Van Loan C F.Matrix computation［M］.2nd ed.USA:the John HopKins University Press，1989.

Underdeterm ined direction of arrival estimation based on spatial time-frequency distributions

ZHU Liwei1，2，WANG Ya1，WANG Xiang2，HUANG Zhitao2
(1.College of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China；2.The State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System，Luoyang 471003，China)

In the field of array signal processing，direction of arrival(DOA)estimation is a hotspot problem.Classical DOA estimation methods usually require the number of sensor should be larger than the source signals’(which the so-called over-determined case is).However，whatwe encounter in practice is always the underdetermined case in which the number of source signal is larger than the sensors’.To solve the problem，amultiple signal classification(MUSIC)extension algorithm based on spatial time-frequency distribution was proposed to achieve the underdetermined DOA estimation by expanding the dimension of the spatial time-frequency distributionsmatrices.Compared with the existing timefrequency MUSIC，the proposed algorithm can be applied to both the over-determined and the underdetermined cases.The proposed algorithm also has advantages over the existing underdetermined DOA estimation methods for it guarantees the estimation precision，relaxes the requirements for source signal sparseness and lowers standards of the number of snapshots.Simulation results confirm the validity and high performance of the proposed algorithm.

direction of arrival；time-frequency distributions；underdetermined

TN911

A

1001-2486(2015)05-149-06

10.11887/j.cn.201505023

http://journal.nudt.edu.cn

2014-09-28

CEMEE国家实验室开放课题基金资助项目(2014K104B)；国家自然科学基金资助项目(61401490)

朱立为(1985—)，男，湖南郴州人，博士研究生，E-mail:iendwin@163.com；黄知涛(通信作者)，男，教授，博士，博士生导师，E-mail:taldcn@yahoo.com.cn