平流层长航时气球上升过程超冷现象影响因素分析*

杨希祥，侯中喜，麻震宇(国防科技大学航天科学与工程学院，湖南长沙410073)

平流层长航时气球上升过程超冷现象影响因素分析*

杨希祥，侯中喜，麻震宇
(国防科技大学航天科学与工程学院，湖南长沙410073)

平流层长航时气球超冷现象是指内部浮升气体温度低于外界大气温度，超冷会引起浮力损失进而阻碍气球上升过程。建立了长航时气球辐射、对流等热模型和上升过程动力学模型，仿真分析了初始净浮力、蒙皮热物性参数、放飞时间和放飞日期等因素对超冷现象的影响规律。研究结果表明，上升过程内外温差随初始净浮力增大而增大且变化显著，可见光吸收率和红外吸收率增大时，内外温差值总体上呈减小趋势；放飞时刻和放飞日期对超冷现象影响较小，但放飞时间不同，气球上升至设计驻空高度的时间差别较大。该结论可为平流层浮空器总体方案设计和放飞试验提供有益参考。

平流层长航时气球；上升过程；超冷现象；热模型

近年来，在对地观测、导弹预警、移动通信等军民应用需求的强力推动下，临近空间持久区域驻留飞行器的发展受到各国高度关注［1］。平流层长航时气球是典型的持久区域驻留飞行器，也是目前唯一真正实现在临近空间高度(约20～100km)长期工作的浮空类飞行器。

平流层长航时气球依靠浮力升空。在上升过程中，气球经历外界环境参数的大幅变化，大气密度、温度、压力随高度增加呈总体下降趋势，随外界大气压力下降，气球快速膨胀对外做功，引起内部浮升气体(通常为氦气)温度大幅下降并低于外界大气温度，产生超冷问题。超冷会造成浮力的大幅损失，严重影响气球上升过程，甚至导致无法上升至预定高度。同时，平流层长航时气球在上升过程中与外界存在复杂的辐射、对流等换热过程，包括太阳辐射、红外辐射、蒙皮对外辐射、蒙皮与外界大气和内部气体间对流换热等。分析平流层长航时气球上升过程动力学与热力学耦合特性，掌握主要设计参数和外界环境因素对超冷问题的影响规律，对于气球成功安全上升至关重要。

国内外很多文献对传统零压气球和超压气球上升和驻留过程航迹仿真问题进行了研究。Kreith和Kreider首先研究了零压气球性能预测问题［2］，Carlson和Horn建立了考虑浮升气体不透明的高空科学气球热与轨迹模型［3］。Franco等以美国国家航空航天局的科学气球为例，研究了科学气球受热问题［4］。Selby采用三维热/流动耦合计算分析方法研究了高空科学气球在漂浮阶段的性能，并改进了用于预测高空气球轨迹的计算机软件SINBAD［5］。方贤德等对超压气球上升和驻留阶段热与轨迹性能预测问题进行了深入研究［6-7］，吕明云等也进行了类似研究［8］。此外，研究人员对平流层飞艇热与轨迹预测问题也开展了建模与仿真研究［9］。

本文建立平流层长航时气球上升过程动力学与热力学耦合模型，研究上升过程超冷现象，重点研究气球设计参数及外界工况对超冷现象的影响规律，为平流层浮空器方案设计、飞行试验方案制定和放飞操作等提供理论参考。研究的平流层气球内部浮升气体采用氦气，大气模型采用美国1976标准大气模型。

1 平流层长航时气球热模型

平流层长航时气球蒙皮温度的变化根据能量平衡方程得到:

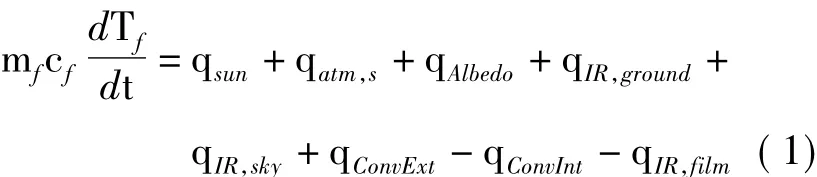
式中，mf，cf，Tf分别为蒙皮质量、蒙皮比热、蒙皮温度，qsun是单位时间吸收的太阳直接辐射量，qatm，s为单位时间吸收的大气散射辐射量，qAlbedo为单位时间吸收的地面反射辐射量，qIR，ground为单位时间吸收的地面红外辐射量，qIR，sky为单位时间吸收的大气红外辐射量，qConvExt为蒙皮与外界大气间单位时间对流换热量，qConvInt为蒙皮与氦气间单位时间对流换热量，qIR，film为单位时间蒙皮对外红外辐射量。

假定气球内部气体满足理想气体定律，且气体温度和压力均匀，则根据热力学第一定律，可得到氦气温度变化率［2］:

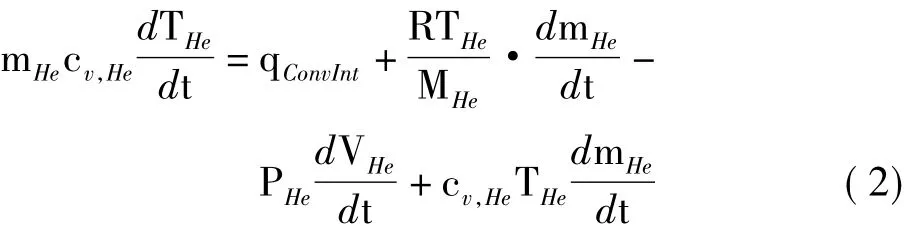
式中，mHe为氦气质量，cv，He为氦气定容比热，R为气体常数，MHe，THe，VHe，PHe分别为氦气分子量、温度、体积、压强。等号右端第一项表示氦气与蒙皮间传热量，第二项是由于氦气排放产生的流动功，第三项为气球体积膨胀对外所做的功，最后一项为由于气体排放损失的内能。

1.1 太阳直接辐射

平流层长航时气球所处高度太阳直接辐射强度为:

式中，τatm为大气透射率，Isun为大气层外的太阳辐照量，可用式(4)近似计算:

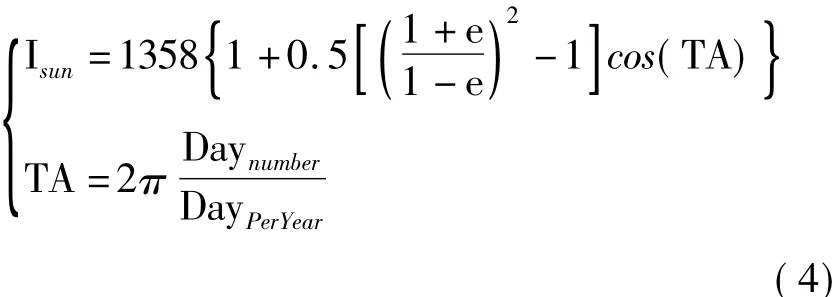
其中，e为地球偏心率，Daynumber为从近日点起算的气球飞行的天数序列，DayPerYear为一年中的天数序列。因为地球偏心率很小，可用平均近点角TA近似真近点角。

τatm与太阳入射角θh的关系可近似如式(5)［2］:

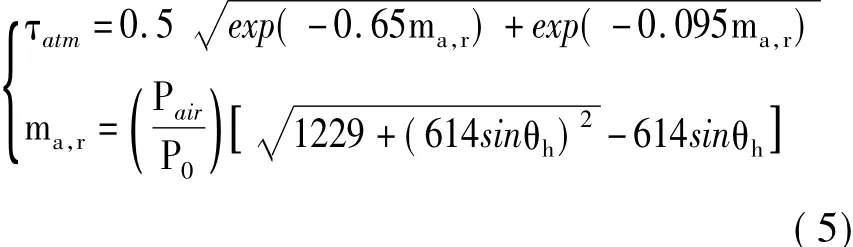
其中，Pair为气球所在高度的大气压强，P0为海平面大气压强。

蒙皮吸收的太阳直接辐射可按式(6)计算:

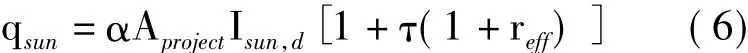
式中:α和τ分别为蒙皮对太阳辐射的吸收率和透射率；Aproject为照射投影面积；reff为蒙皮对太阳辐射的有效反射率，反映了太阳光透射后在蒙皮内部经多次反射被吸收的情况，定义为:

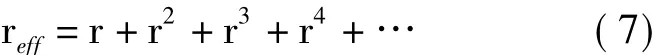
式中，r为蒙皮对太阳辐射的反射率。

1.2 大气散射辐射

大气散射太阳辐射强度根据式(8)计算:

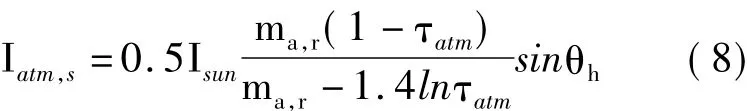
蒙皮吸收的大气散射太阳辐射强度按式(9)计算:

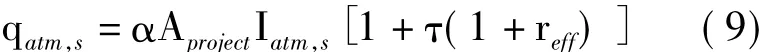
1.3 地面反射辐射

地面反射太阳辐射强度按式(10)计算:

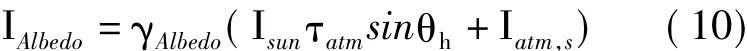
蒙皮吸收的地面反射太阳辐射强度为:

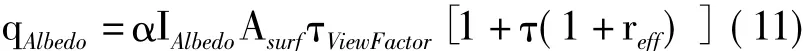
其中，γAlbedo为地面平均反射率，Asurf为气球表面积，τViewFactor为地球表面对蒙皮表面的角系数，且有［10］:式中，z为气球高度。

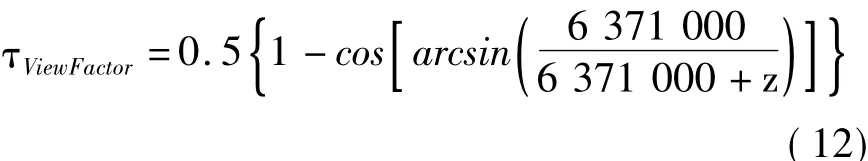
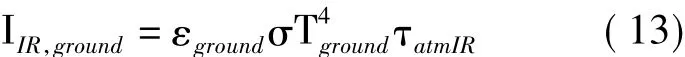
1.4 地面红外辐射

平流层长航时气球所处高度地面红外辐射强度为:

式中，εground为地面平均红外发射率，σ为斯特潘波尔茨曼常数，τatmIR为红外辐射的大气透射率。

蒙皮对地面红外辐射的吸收根据式(14)计算:

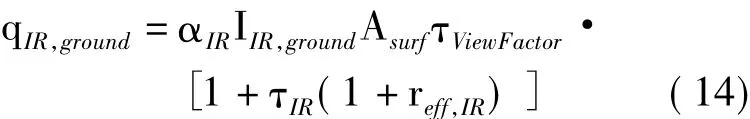
式中:αIR为蒙皮对红外辐射的吸收率；τIR为蒙皮对红外辐射的透射率；reff，IR为有效反射率，定义为:

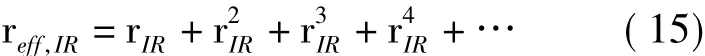
式中，rIR为蒙皮对太阳辐射的反射率。

1.5 大气红外辐射

计算大气红外/长波辐射时，将周围大气环境看作黑球模型。气球所处高度大气红外辐射强度为:

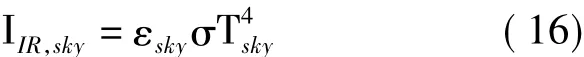
式中，εsky为地面平均红外发射率，Tsky为天空等效黑球温度，且有:

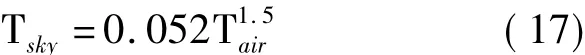
蒙皮对大气红外辐射的吸收根据式(18)进行计算:

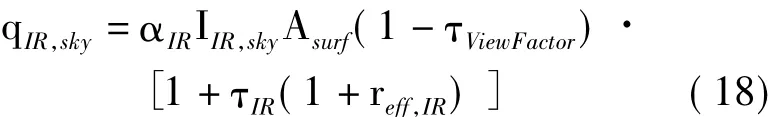
1.6 蒙皮与外界大气对流换热

蒙皮与外界大气环境的对流换热包括自然对流与强迫对流两部分。对流换热表示如式(19):

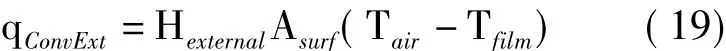
式中，Hexternal为外部对流换热系数，按式(20)计算:

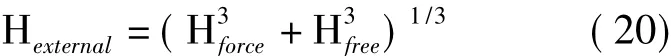
式中，Hforce为强迫对流换热系数，Hfree为自然对流换热系数，其与Nusselt数的关系为:

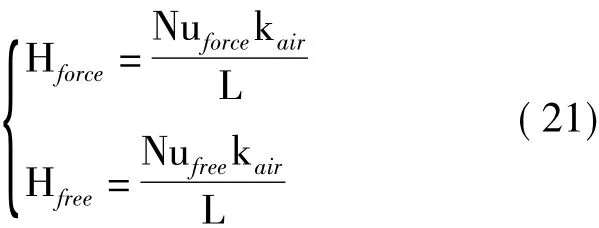
式中，kair为空气热传导率，Nuforce为外部强迫对流对应的Nusselt数，Nufree为外部自然对流对应的Nusselt数，L为特征长度，对于球形，L=d(d为直径)。相关参数计算公式如式(22)所示［10］。

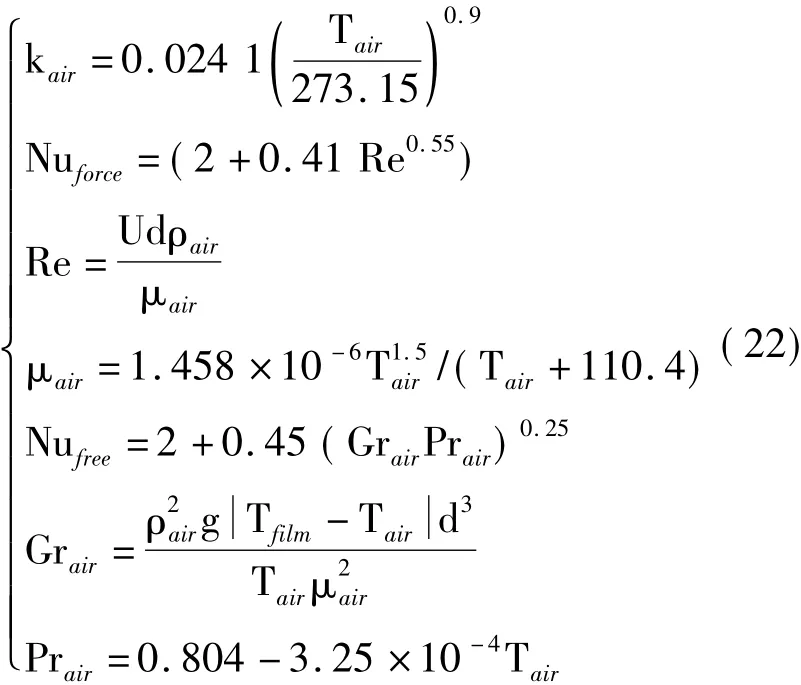
其中，Re为雷诺数，U为垂直方向速度，μair为空气的动力黏性系数，Grair为空气的格拉晓夫数，Prair为空气的普朗特数。

1.7 蒙皮与氦气对流换热

蒙皮与氦气对流换热属自然对流，计算公式如式(23)。

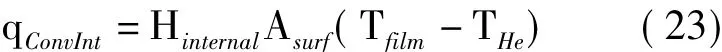
式中，Hinternal为内部对流换热系数，按式(24)计算:

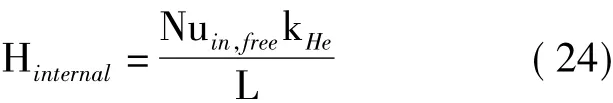
式中，Nuin，free为内部自然对流对应的Nusselt数，kHe为氦气的热传导率，相关参数计算公式如式(25)［10］:

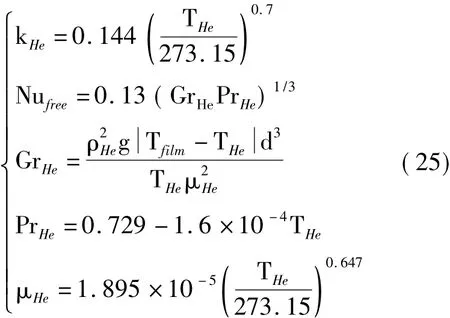
其中，μHe为氦气的动力黏性系数，GrHe为氦气的格拉晓夫数，PrHe为氦气的普朗特数。

1.8 蒙皮红外辐射

蒙皮的红外辐射包括外蒙皮对外部环境的红外辐射和蒙皮内表面的红外辐射:

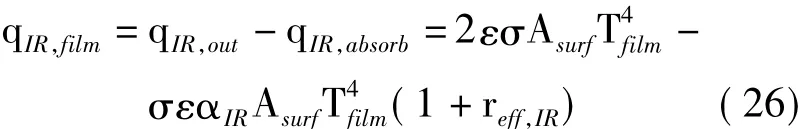
式中，ε为蒙皮材料平均红外发射率，根据基尔霍夫定律，αIR=ε，等号右端第一项为蒙皮内外表面对外红外辐射总强度，第二项为被内表面吸收的部分。

2 平流层长航时气球动力学模型

平流层长航时气球上升段受到的力包括浮力、重力、气动阻力，垂直方向的动力学方程可表示为(以高度垂直向上为正):

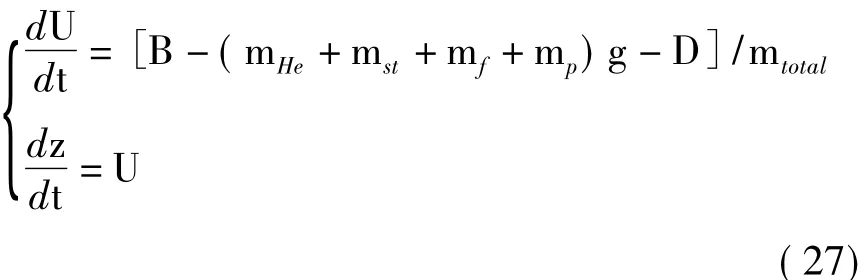
其中，mtotal为考虑附加质量在内的总质量，z为高度，U为垂直方向速度，B为总浮力，mHe为氦气质量，mst为包括桁架、吊舱、电源、推进系统、飞控、压控等在内的系统干重，mf为蒙皮质量，mp为有效载荷质量，D为气动阻力，且有:

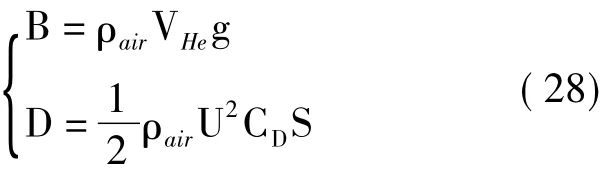
其中:VHe为氦气体积，由热力学模型计算得到；CD为阻力系数；S为气球参考面积。

式(27)中的总质量mtotal表示为如式(29)所示的形式。

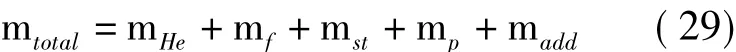
式中，madd为由于浮力，囊体带动周围空气运动而引起的附加质量，且有:

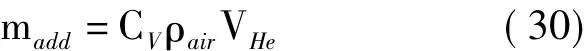
式中，CV为附加质量系数。

对于平流层长航时气球来说，动力学与热力学的耦合主要体现在垂直方向运动上，因此，暂不考虑水平面内运动。上升过程中，阀门开关控制是内外压差、上升速度的函数，若内外压差过大或上升速度过快，可通过排气阀向外排放氦气进行调节，排气方程为:

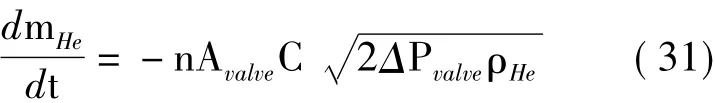
式中:n为阀门数量；Avalve为单个阀门横截面积；C为排气系数，考虑理论流动和实际流动的差异得到；ΔPvalve为阀门内外压差。

3 仿真结果与分析

以某平流层长航时超压气球为例，采用上述建立的动力学模型和热模型，分析超冷现象影响因素及影响规律。仿真所用气球参数如表1所示。气球上升过程通过阀门适当排放氦气以控制上升速度和内外压差。

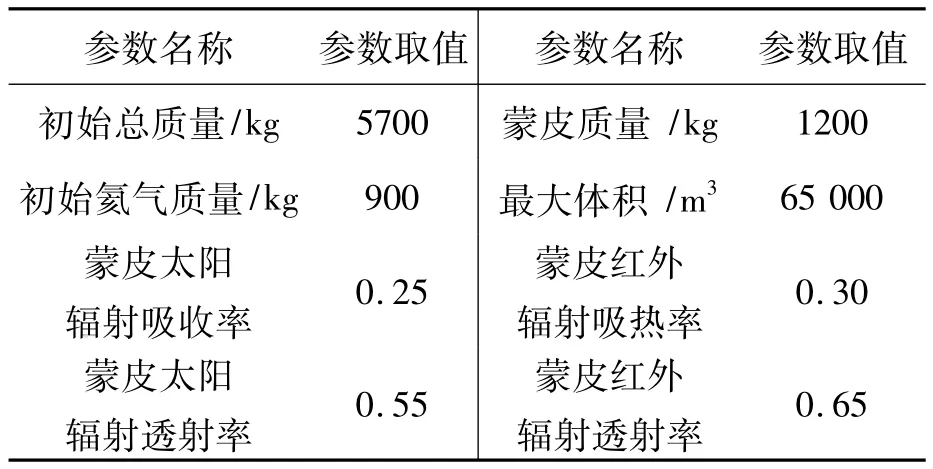
表1 平流层长航时气球主要参数Tab.1 Main parameters of a stratospheric long duration balloon

3.1 初始净浮力影响

初始净浮力影响气球上升速度，进而影响超冷现象。初始净浮力和气球初始总重量的比值分别取10%，15%，25%时，上升过程速度和内外温差(大气温度-氦气温度)变化曲线如图1～2所示。

由图可以看出，随初始净浮力值增大，上升过程速度极值和平均值逐渐增大且变化明显，上升过程内外温差值随速度增大而增大，内外温差最大值由净浮力为10%时的14.5K增加到净浮力为25%时的31.9K，较大的温差引起较大的净浮力损失。因此，对于非成形升降方式来说，需选择合理的初始净浮力或采用有效措施控制上升速度。

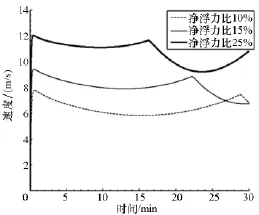
图1 上升速度-时间曲线Fig.1 Ascent velocity versus time

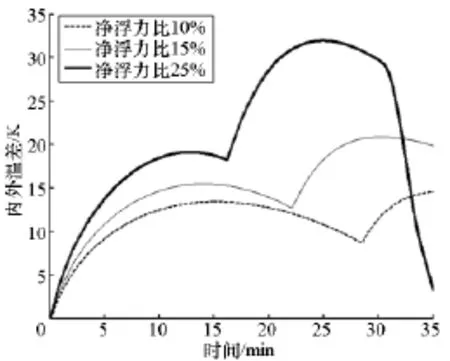
图2 温差-时间曲线Fig.2 Temperature difference versus time

3.2 蒙皮热物性参数影响

蒙皮热物性参数包括蒙皮对太阳辐射和红外辐射的吸收率、反射率、透射率，蒙皮红外发射率等。这里主要分析太阳辐射吸收率和红外辐射吸收率影响规律。红外吸收率取0.3，蒙皮对太阳辐射的吸收率分别为0.05，0.25，0.45时，内外温差变化如图3所示；太阳辐射吸收率取0.25，红外吸收率分别取0.05，0.20，0.35时，内外温差变化如图4所示。

由图可以看出，高可见光吸收率和高红外吸收率对缓解上升过程内外温差具有一定作用，吸收率增大时，内外温差值总体上呈减小趋势，太阳辐射吸收率对超冷的影响大于红外吸收率影响，太阳辐射吸收率最大值和最小值对应峰值温差相差约为10K。红外吸收率的影响规律较为复杂，是因为在热模型中采用了红外吸收率等于红外发射率的基尔霍夫定律。需要说明的是，对外界辐射的高吸收率会导致留空期间超热问题严重加剧(图3温差转负值后)。因此，蒙皮材料热物性参数选择应综合考虑上升过程与留空过程。与上升速度影响的仿真结果对比还说明，对流换热对于超冷的影响大于辐射。

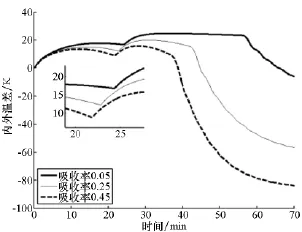
图3 太阳辐射吸收率影响Fig.3 Influence of solar radiation absorptivity

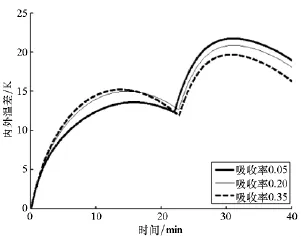
图4 红外辐射吸收率影响Fig.4 Influence of infrared radiation absorptivity

3.3 外界热环境影响

外界热环境变化包括放飞时间、放飞地点、地表红外辐射状况变化、地表对太阳辐射的反射情况变化等。这里主要分析放飞时刻和放飞日期影响。放飞时刻分别取4点、12点和16点时，内外温差变化如图5所示。放飞时刻设定为中午12点，放飞日期分别为3月21日、6月30日、12月21日时，内外温差变化如图6所示。

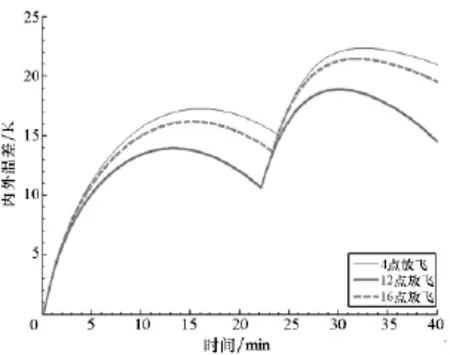
图5 放飞时刻影响Fig.5 Influence of launch time epoch

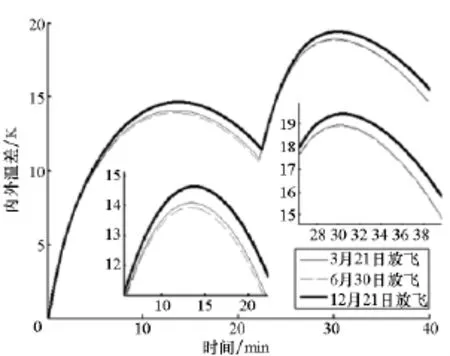
图6 放飞日期影响Fig.6 Influence of launch date

由图5可以看出，放飞时刻不同时，温差极大值相差不大，凌晨4点放飞与中午12点放飞，温差极大值相差不大于5K，原因在于:辐射强度较高时，平均上升速度快，气球膨胀速度快，但从外界吸收的太阳辐射量相对较多；辐射条件较差时，从外界吸收的太阳辐射热量小，但平均上升速度慢，气球膨胀速度慢。辐照条件较好时，温差稍小，超冷现象稍有减缓。需要说明的是，放飞时刻不同，气球上升至驻留高度的时间差别较大，凌晨4点放飞，升空时间约2500s，中午12点放飞，升空时间则约3000s。

由图6可以看出，放飞时刻相同时，放飞日期对上升过程超冷现象影响很小。

4 结论

建立了平流层长航时气球热模型和上升过程动力学模型，分析了初始净浮力、蒙皮热物性参数、放飞时间和放飞日期等因素对上升过程超冷现象的影响规律。结果表明，上升过程内外温差值随初始净浮力增大而增大且变化显著，选择合理的初始净浮力，或采用有效措施控制上升速度极为重要；高可见光和红外吸收率对缓解内外温差具有一定作用，吸收率增大时，内外温差值总体上呈减小趋势，但蒙皮热物性参数总体影响小于初始净浮力，反映了上升过程辐射对超冷现象的影响小于对流换热影响；放飞时刻和放飞日期对超冷现象影响较小，但放飞时刻不同，气球上升至设计驻空高度的时间差别较大。

References)

［1］Knoedler A J.Lowering the high ground:using near-space vehicles for persistent ISR［D］.USA:Air University，2005.

［2］Kerith F，Kerider J F.Numerical prediction of the performance of high altitude balloons［R］.USA:National Center for Atmospheric Research，1974.

［3］Carlson L A，Horn W J.A new thermal and trajectory model for high altitude balloons［C］//Proceedings of 7th AlAA Aerodynamic Decelerator and Balloon Technology Conference，1981:1-9.

［4］Franco H，Cathey H M，Jr.Thermal performancemodeling of NASA’s scientific balloons［J］.Advances in Space Research，2004，33(10):1717-1721.

［5］Selby G V.Archive Set［R］.USA:American Institute of Aeronautics and Astronautics，1997.

［6］戴秋敏，方贤德，王昊，等.大气模型对高空气球运动特性和热特性的影响［J］.计算机仿真，2013，30(9):79-82.DAIQiumin，FANG Xiande，WANG Hao，et al.Simulation of influence of different atmospheric models on dynamic and thermal properties of high altitude balloons［J］.Computer Simulation，2013，30(9):79-82.(in Chinese)

［7］Li X J，Fang X D，Dai QM，et al.Modeling and analysis of floating performances of stratospheric semi-rigid airships［J］.Advances in Space Research，2012，50(7):881-890.

［8］吕明云，巫资春.高空气球热力学模型与上升过程仿真分析［J］.北京航空航天大学学报，2011，37(5):505-509.LYU Mingyun，WU Zichun.Thermodynamic model and numerical simulation of high altitude balloon ascending process［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37(5):505-509.(in Chinese)

［9］姚伟，李勇，范春石，等.复杂热环境下平流层飞艇高空驻留热动力学特性［J］.宇航学报，2013，34(10): 1309-1315.YAOWei，LI Yong，FAN Chunshi，et al.Heat dynamics behavior of a stratospheric airship in a complex thermal environment at high-altitude station-keeping conditions［J］.Journal of Astronautics，2013，34(10):1309-1315.(in Chinese)

［10］Farley R E.Balloon ascent:3-D simulation tool for the ascent and float of high-altitude balloons［C］//Proceedings of 5th AlAA Aviation，Technology Integration and Operations Conference，Arlington.Virginia，AIAA 2005-7411，2005: 1-15.

Analysis of influential factors to supercooling phenomenon during ascent stage of stratospheric long duration balloons

YANG Xixiang，HOU Zhongxi，MA Zhenyu
(College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China)

Supercooling phenomenon ofstratospheric long duration balloonsmeans that the temperature ofhelium gas inside is lower than thatof atmosphere outside，thiswill cause the loss of buoyancy and affect ascent process of the balloon as a result.Radiation and convection thermal models and the vertical dynamicmodel of long duration balloonswere established，and the influence regularity of some important factors，including initial netbuoyancy，skin thermal physical parameters，launch time and launch date，on supercooling phenomenon wasanalyzed.Simulation results show that the temperature difference between helium gas and outside atmosphere enlarges remarkably alongwith the increase of initialnetbuoyancy，and the temperature difference decreaseswhen the absorptivity for visible lightand infrared radiation increases.Simulation results also show that the influence of launch time and launch date on supercooling phenomenon ismuch smaller，while flight time from ground to designed altitude displays great difference when the launch time is different.The research results can provide theoretical reference for conceptual design and flight test.

stratospheric long duration balloon；ascent stage；supercooling phenomenon；thermalmodel

V274

A

1001-2486(2015)05-091-06

10.11887/j.cn.201505014

http://journal.nudt.edu.cn

2015-01-20

高分辨率对地观测系统重大专项资助项目(GFZX040201)

杨希祥(1982—)，男，河北阜城人，副教授，博士，E-mail:nkyangxixiang@163.com