MIMO雷达比幅单脉冲测角精度分析

2015-06-19张娟娟刘红明

系统工程与电子技术 2015年1期

关键词：单脉冲测角理论值

李军，王珍，张娟娟，刘红明

（电子科技大学电子工程学院，四川成都611731）

MIMO雷达比幅单脉冲测角精度分析

李军，王珍，张娟娟，刘红明

（电子科技大学电子工程学院，四川成都611731）

和差比幅单脉冲测角方法由于实现简单且测角精度高，在雷达系统中得到广泛应用。研究多输入多输出（multiple-input multiple-output，MIMO）雷达的比幅单脉冲测角技术及其精度问题，采用全微分方法详细推导了MIMO雷达和传统相控阵雷达的单脉冲测角精度，得到了准确的测角误差函数表达式。通过计算机仿真，验证了理论分析的正确性，并在相同信噪比条件下，对两种模式下的测角精度进行了比较。

多输入多输出雷达；比幅单脉冲测角；精度分析；全微分法

0 引言

多输入多输出（multiple-input multiple-output，MIMO）雷达［1-4］发射端采用相互正交的信号，在空间形成宽的低增益发射波束，在接收端则采用同时多波束处理。MIMO雷达较之传统雷达有许多新特性，在目标分辨、低速目标检测、抗截获等方面有很大的优势，成为了当今雷达界的研究热点。

工程上常用的目标角度测量方法中，单脉冲测角方法实现简单，并具有测角精度高、抗干扰能力强等优点，故在精密跟踪雷达测量中得到了广泛应用［5-11］。文献［12］首先将比幅单脉冲测角应用于MIMO雷达，文献［13］研究了比相单脉冲测角在MIMO雷达中的应用，文献［14］则分析了信号相关性对测角误差的影响。这些关于单脉冲测角技术的研究中，缺少对测角精度的理论推导，往往只给出了测角精度与信噪比的关系［15］，更没有MIMO雷达和相控阵雷达测角精度的定量分析。本文针对此问题进行了研究，详细推导了测角精度的理论表达式，得到了测角精度与阵元数、信噪比、左右波束间隔的关系式。

1 振幅和差单脉冲测角的基本原理

假定有两个相同且彼此部分重叠的波束，其示意图如图1所示，两个波束交叠于OA轴，当目标位于θs方向时，两个波束收到的信号强度相当，故称此轴为等信号轴；当目标偏向OB方向时，指向θl的左波束的回波要强一些；当目标偏向OC方向时，指向θr的右波束的回波要强一些。因此，通过比较左、右波束中目标回波信号的强弱可以判定目标偏离和波束指向θs的方向。这就是和差比幅单脉冲测角法［6，12］的基本原理。

图1 相邻两波束示意图

采用上述方法测角时，设左、右及和波束方向图函数分别为F（θl）、F（θr）和F（θs），如图2所示。

图2 交于半功率点的相邻两波束

可得误差电压

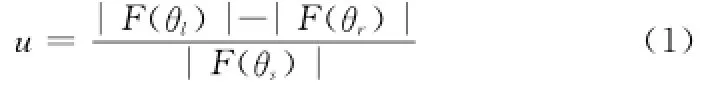
MIMO雷达方向图函数［12］为

式中，F（θl）和F（θr）表达式与F（θs）类似；N和M为收发阵元数；dr和dt为收发阵元间距。

振幅和差单脉冲测角法应用于相控阵雷达和MIMO雷达中的不同之处在于：MIMO雷达除了进行接收信号的匹配滤波和接收波束形成之外，还要进行等效发射波束形成以得到联合方向图来进行测角。在相同天线阵列布置下，MIMO雷达的联合方向图的主瓣宽度较相控阵雷达的方向图的主瓣宽度要窄［12］，说明MIMO雷达测角精度应比相控阵雷达更高。

2 MIMO雷达理论测角精度

设目标偏离和波束指向的值为Δθ，在连续跟踪状态通常有Δθ≪θ3dB，即目标位于差波束零值（和波束最大值）附近，则差波束方向图FΔ（Δθ）可在差波束零值（Δθ＝0）处展开

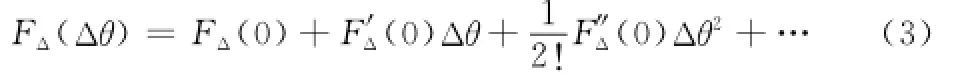
若忽略二阶导数以上的各项，并考虑到FΔ（0）≈0［5］（差波束零值深度很低），则

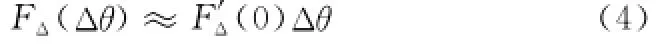
而且在和波束最大值附近有

用和波束半功率点宽度θ3dB对Δθ进行归一化，则误差电压可以表示为

故与接收机噪声引起的误差电压均方根值σΔu对应的目标角度测量误差均方根值σΔθtgt为

相控阵中，可用高斯函数拟合方向图的方法求k［5］。

mMIMO雷达方向图与相控阵雷达具有相似的形式，所以也可采用高斯函数来拟合方向图主瓣，则左、右及和波束方向图可分别表示为

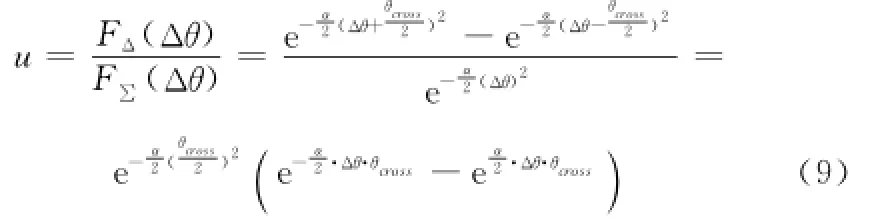
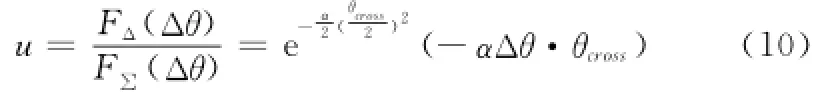
代入α的值并求导可得

于是有

对收发共用的M阵元均匀线阵，MIMO雷达阵列接收的左、右、和波束的方向图函数为

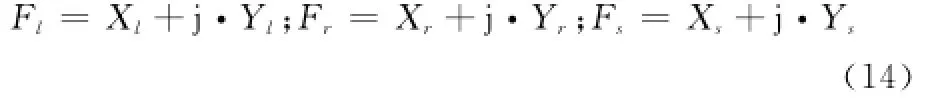
则和差比幅单脉冲测角的误差电压为

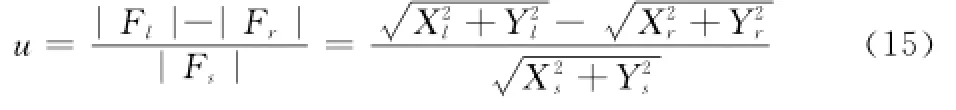
其全微分为

假设|θl－θr|＝θcross，记和波束指向位置的接收左、右及和波束的幅度分别为

|Fs|＝A0＝M2；|Fl|＝|Fr|＝A1（17）例如|θl－θr|＝θ3dB时，|Fl|＝|Fr|＝，由式（17）得

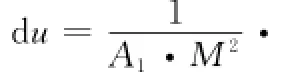
［（Xl·d Xl＋Yl·d Yl）－（Xr·d Xr＋Yr·d Yr）］（18）

若考虑接收机噪声的影响，且为了简化分析，假设θs＝θtgt＝0，即目标在天线阵元法线方向，接收波束指向对准目标，则b（θs）＝a（θtgt）＝［1，1，…，1］T∈NM×1，V为噪声向量，记b（θl）＝b*（θr）＝bI＋j·bQ（19）

V＝vI＋j·vQ∈CM×M（20）式中，vIig，vQig、Vij分别为VI，VQ，V中的元素，vIij，vQij～N（0，σ2／2），即Vij～N（0，σ2）（i，j＝1，2，…，M），且

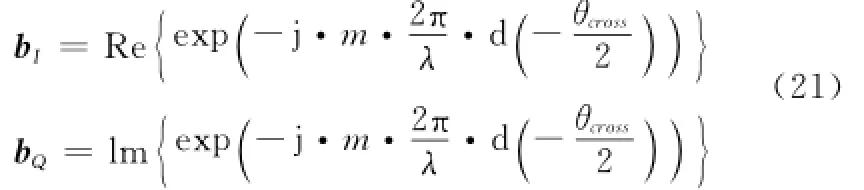
其中，m＝0，1，…，M－1。则MIMO雷达的接收左、右波束分别为

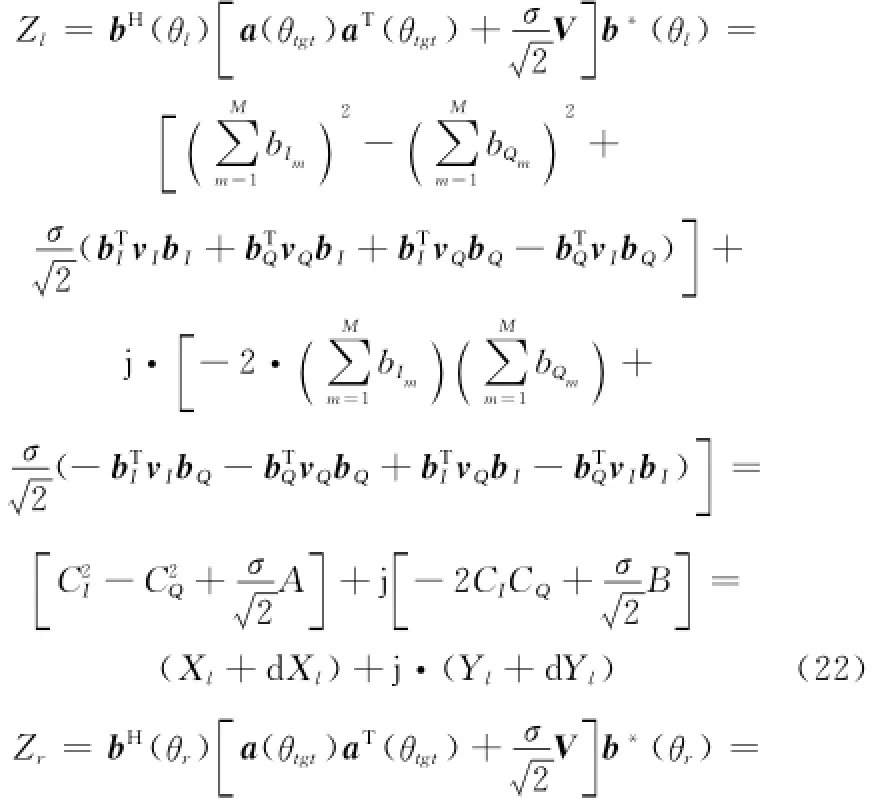
将式（22）、式（23）中各对应项代入式（18），可得

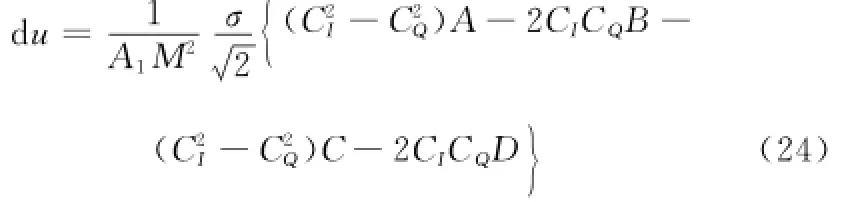
其方差为

因为和波束方向输出信噪比为

式中，C由式（27）可以看出，MIMO＝＝雷达的误差电压均方误差σ2Δu与左右波束的间隔|θl－θr|＝θcross有关，将式（27）、式（13）代入式（7）可得MIMO雷达的测角精度。

3 相控阵雷达的理论测角精度

对于相控阵雷达，σΔθtgt与σΔu、km及θ3dB的关系与MIMO雷达相同，重写为

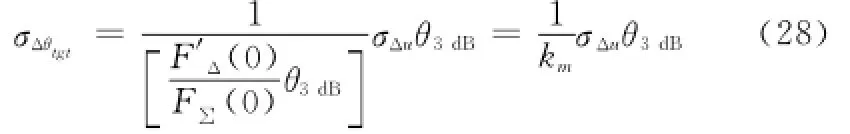
其中归一化斜率也可通过高斯函数拟合方向图得到，重写为

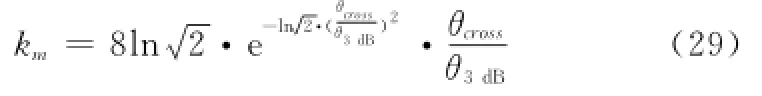
由于相控阵雷达发射信号波形以及接收信号的匹配滤波、波束形成与MIMO雷达均有所区别，所以相控阵雷达进行和差比幅单脉冲测角得到的误差电压与MIMO雷达不相同，其误差电压均方误差也不相同，以下给出σ2Δu的具体推导过程。

与MIMO雷达相同，相控阵雷达方向图函数也可用式（14）表示，所以误差电压的全微分形式也可以表示为

b（θs），a（θtgt），b（θl）的定义跟MIMO雷达相同，噪声向量记为则接收左、右波束分别为

将式（32）、式（33）中各对应项代入式（30），可得

因为和波束方向输出信噪比为

所以误差电压的方差

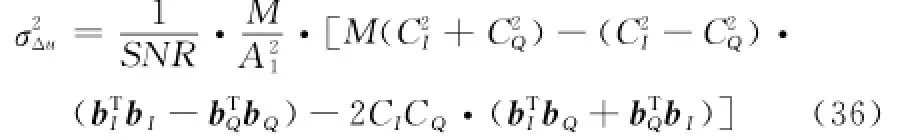
式中，A1，CI，CQ，bI，bQ均为左右波束间隔|θl－θr|＝θcross的函数，即误差电压均方误差与左右波束的间隔有关。将式（36）、式（29）代入式（28）即可得相控阵雷达和差比幅单脉冲测角精度。

4 仿真验证

4.1 相控阵雷达

仿真条件：均匀线阵阵元数M＝10，阵元间距为半波长，可计算出θ3dB＝10．2°，θ2dB＝8．4°，若θcross＝θ3dB则

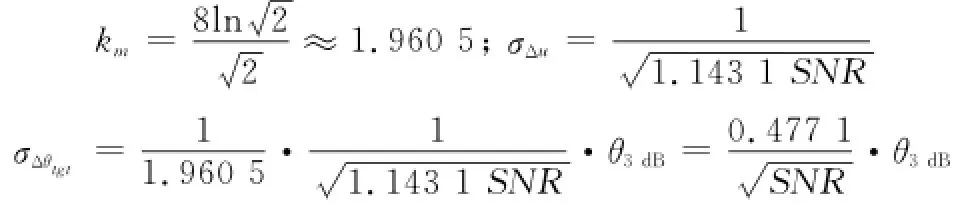
图3是左右波束间隔为θ3dB时，相控阵雷达误差电压理论值与仿真值的对比关系图。仿真值是信噪比从10 dB变化到50 dB时2 000次蒙特卡罗仿真统计得到的误差电压结果，理论值由式（27）推导得到。从图3可以看出，理论值与仿真值几乎吻合，说明了式（27）的有效性。

图3 相控阵雷达误差电压理论值和仿真值随信噪比变化曲线

图4 是左右波束间隔为θ3dB时，相控阵雷达测角精度理论值与仿真值的对比关系图。的仿真值与本文第3节推导的理论值之间的误差稍微大一些，这是由于仿真时，拟合宽度为0.002，即拟合斜率近似为误差电压零点的斜率，得到斜率的仿真值为11.906 9，由归一化斜率得到理论值为11.012 6，虽然理论值与仿真值已经非常接近，但还是稍有误差，再加上仿真的随机性，共同造成了的仿真值与理论值之间的误差。

图4 相控阵雷达测角精度理论值和仿真值与SNR关系的对比

需要说明的是，本文推导测角精度时采用了高斯函数拟合，得到的理论精度值只是近似值，并不是严格意义上的测角精度的下界，所以可能出现图4中仿真值优于理论值的情况。

4.2 MIMO雷达

仿真条件：均匀线阵阵元数M＝10，阵元间距为半波长，可计算出θ3dB＝7．4°，θ2dB＝6°，若θcross＝θ3dB则

仿真结果如图5和图6所示。

图5 MIMO雷达误差电压理论值与仿真值随信噪比变化曲线

图6 MIMO雷达测角精度理论值和仿真值与SNR关系的对比

由图5和图6可知，MIMO雷达的测角精度对比验证结果与相控阵雷达相同，不再重复。

4.3 两种雷达模式的对比

两种雷达模式的对比曲线如图7所示。

将MIMO雷达理论的测角精度与相控阵雷达的理论测角精度相对比，即将第4．2节得到的MIMO雷达测角精度和第4.1节得到的相控阵雷达的测角精度对比，可知，在和波束输出信噪比相同时，MIMO雷达比幅测角精度高于相控阵雷达比幅测角精度（首先MIMO雷达θ3dB较小，其次常数0．454 6比0．477 1稍小），通过图7的测量值也可以看出，MIMO雷达比幅测角精度高于相控阵雷达比幅测角精度。

图7 MIMO雷达和相控阵对比曲线

5 结论

本文简单介绍了振幅和差单脉冲测角的基本原理，并用高斯函数拟合方向图的方法求出了归一化斜率km，然后采用全微分法推导了MIMO雷达和相控阵雷达的误差电压均方误差的公式，根据测角精度与km、误差电压均方误差、θ3dB的关系得到了测角精度的理论公式，并得出测角精度与左右波束间隔有关。然后通过仿真验证了理论推导跟仿真实验值是基本吻合的。由于MIMO雷达的联合方向图的主瓣宽度较相控阵雷达的方向图的主瓣宽度要窄，因而测角精度更高，所以文中还在相同条件下对相控阵雷达和MIMO雷达的测角精度进行了对比，得出MIMO雷达的测角精度的确要比相控阵雷达的精度高。

［1］Li J，Stoica P．MIMO radar with colocated antennas［J］．Signal Processing Magazine，2007，24（5）：106- 114．

［2］Haimovich A M，Blum R S，Cimini L J．MIMO radar with widely sepatated antennas［J］．IEEE Signal Processing Magazine，2008，25（1）：116- 129．

［3］He Z S，Han C L，Liu B．MIMO radar and its technical characteristic analyses［J］．Acta Electronica Sinica，2005，33（12A）：2441- 2445．（何子述，韩春林，刘波．MIMO雷达概念及其技术特点分析［J］．电子学报，2005，33（12A）：2441- 2445．）

［4］Fishler E，Haim ovich A，Blum R S，et al．Spatial diversity in radars models and detection performance［J］．IEEE Trans.on Signal Processing，2006，54（3）：823- 828．

［5］Zhang G Y．Phased array radar principle［M］．Beijing：National Defense Industry Press，2001．（张光义．相控阵雷达原理［M］．北京：国防工业出版社，2001．）

［6］Yang S Q，Xu S T，Chen W D，et al．Resolution method of multiple jammers for passive monopulse radar［J］．Journal of Electronics&Information Technology，2002，24（10）：1346- 1351．（杨绍全，徐松涛，陈卫东，等．无源单脉冲雷达多干扰源目标分辨方法［J］．电子与信息学报，2002，24（10）：1346- 1351．）

［7］Wei B Y，Zhu D Y，Wu D，et al．An airborne SAR geolocation approach based on sum-difference beam SAR imagery［J］．Journal of Electronics&Information Technology，2013，35（6）：1464- 1470．（韦北余，朱岱寅，吴迪，等．一种基于和差波束的机载SAR定位方法［J］．电子与信息学报，2013，35（6）：1464 -1470．）

［8］Zhu W，Chen B X，Zhou Q．Angle measurement method with digital mono-pulse for 2-dimensional digital array radar［J］．Systems Engineering and Electronics，2011，33（7）：1503- 1509．（朱伟，陈伯孝，周琦．两维数字阵列雷达的数字单脉冲测角方法［J］．系统工程与电子技术，2011，33（7）：1503- 1509．）

［9］Mohammed J R．A new technique for obtaining wide-angular nulling in the sum and difference patterns of monopulse antenna［J］．Antennasand Wireless Propagation Letters，2012，11：1245- 1248．

［10］Takahashi R，Rokuzo H，Teruyuki H，et al．Monopulse angleestimation for unresolved targets with a fourth order cumulant［C］∥Proc.of the International Symposium Antennas and Propagation，2012：1152- 1155．

［11］Xiong Z Y，Xu Z H，Xiao S P．Subarray partitioning based on the clustering algorithms and the performance of monopulse technology［J］．Systems Engineering and Electronics，2013，35（9）：1867- 1872．（熊子源，徐振海，肖顺平．聚类子阵划分及子阵级单脉冲测角性能分析［J］．系统工程与电子技术，2013，35（9）：1867- 1872．）

［12］He Q，He Z S，Li H Y．Multibeam amplitude comparison problems for MIMO radar’s angle measurement［C］∥Proc.of the Asilomar Conference on Signal，Systems and Computers，2007：2163- 2167．

［13］Zhang J K，Liu H M，Li J，et al．Research on the mono-pulse phase comparison angle measurement algorithm of MIMO radar［C］∥Proc. of the International Workshop on Microwave and Millimeter Wave Circuits and System Technology，2011：1- 4．

［14］Liu Z，Li J，Liu H M，et al．The mono-pulse angle measurement of non-strictly orthogonal signals for MIMO radar［J］．Radar Science and Technology，2013，11（3）：262- 266．（刘周，李军，刘红明，等．MIMO雷达非严格正交信号单脉冲测角方法［J］．雷达科学与技术，2013，11（3）：262- 266．）

［15］Ding L F．Radar theory［M］．Beijing：Electronic Industry Press，2009．（丁鹭飞．雷达原理［M］．北京：电子工业出版社，2009．）

Angular accuracy analysis of amplitude-comparison mono-pulse angle measurement for MIMO radar

LI Jun，WANG Zhen，ZHANG Juan-juan，LIU Hong-ming
（School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）

The amplitude-comparison of sum and difference beams has been widely used in the radar system，as the method is easy to implement and has a high angular accuracy．The angle measuring technology and analyses of the angular accuracy are focused on．The total differential method is used to derivate the angle measurement precision of the method in the multiple-input multiple-output（MIMO）radar and the phased array radar，and a strict formula of the angle measurement error has been gotten，while the angle measurement accuracy of the two types of radars are compared under the same SNR conditions，and the analysis is verified by simulations．

multiple-input multiple-output（MIMO）radar；amplitude comparison mono-pulse angle measurement；analyses of angular accuracy；total differential method

TN 95

10．3969／j．issn．1001-506X．2015．01．10

李军（1977-），男，副教授，博士，主要研究方向为雷达信号处理、MIMO雷达技术。

E-mail：lijun_sc＠qq．com

王珍（1989-），女，硕士研究生，主要研究方向为MIMO雷达信号处理。

E-mail：946233793＠qq．com

张娟娟（1987-），女，硕士研究生，主要研究方向为MIMO雷达信号处理。

E-mail：1436781922＠qq．com

刘红明（1967-），男，高级工程师，博士，主要研究方向为双多基地雷达、雷达信号处理、MIMO雷达技术。

E-mail：kjlhm＠163．com

1001-506X（2015）01-0055-06