基于量测转换与输入估计的机动目标跟踪算法
2015-06-19赵温波王立明刘发磊
盛 琥,赵温波,王立明,刘发磊,曹 燕
(陆军军官学院,安徽合肥230031)
基于量测转换与输入估计的机动目标跟踪算法
盛 琥,赵温波,王立明,刘发磊,曹 燕
(陆军军官学院,安徽合肥230031)
针对雷达系统中机动目标的跟踪问题,提出输入估计(input estimation,IE)与无偏量测转换(unbiased converted measurement,UCM)相融合的自适应算法。用无偏量测转换技术将观测量转换到直角坐标系,使得在极坐标系内应用IE成为可能;提出检测窗内加速度阶梯变化的假设并推导相关模型,使得单个输入估计器能够跟踪各种变化机动。仿真分析表明,算法与基于多滤波器并行工作的交互式多模型相比,跟踪精度相当,但运算量大大降低,因此适用于对性能和实时性要求较高的场合,有很好的应用前景。
全面自适应跟踪;变加速度跟踪;输入估计;无偏量测转换
0 引 言
机动目标跟踪[1]经过多年研究已发展出多种方法。其中输入估计(input estimation,IE)因具有对匀速运动估计精确,且无需机动先验知识等优点成为研究热点。自文献[2]提出IE原型以来,诸多学者对其修正和改进。文献[3]提出的基于多机动情况假设的IE方法可在一定程度上提高跟踪精度,但其需要多个滤波器并行工作,计算量很大。文献[4]提出以最小化机动估计方差为准则的递归IE方法。文献[5]提出基于伪残差的修正IE算法,通过仿真得出算法优于交互多模(interacting multiple model,IMM)算法的结论;但在其他场景中[6],该算法不比IMM性能优越。文献[7]提出修正的IE算法,通过修正新息序列提高了机动跟踪能力。之后文献[8]提出IMM和IE的融合算法(IMM-IE),既能跟踪变化机动,又使匀速过程精确滤波具备了全面自适应能力。此外,IE还被用于与其他方法的融合中[911]。
尽管IE是一种很有特色的跟踪算法,但其在工程实用中的诸多困难阻碍了它的发展,具体表现为:①算法将机动加速度视为未知的恒定输入,基于此假设进行机动判决、估计和状态补偿,但此假设并不总是成立,比如目标转弯时,加速度时刻变化,如采用IE,假设与实际的严重不符反而会使跟踪误差增大。解决此问题有两种手段:一是减小检测窗长度,使检测窗内的机动特性尽量符合假设,但这会导致输入估计器对弱机动不敏感,跟踪精度降低;二是将不同检测窗长度的IE在IMM算法中融合,但会显著增加计算量。②输入估计的状态和量测方程在直角坐标系建立,而大多数跟踪问题中的量测数据在极坐标系或球坐标系获得,如何将IE实用化也是亟待解决的问题。针对以上两点,本文提出更符合实际的线性机动假设并推导了相应模型,解决了第一个困难;用无偏量测转换(unbiased converted measurement,UCM)[1-214]将极坐标系量测变换到直角坐标系,解决了第二个困难。无偏量测转换和输入估计的融合(UCM-IE),生成一种既能对机动全面适应,又不会显著提高计算量的实用方法。
1 量测转换与输入估计的融合算法
IE是一种优秀的单模算法,其模型基于两个假设:①控制输入在目标机动期间为常数;②机动总是在被检测到后才终止。基于此,算法将机动加速度视为未知的恒定输入,采用常速状态方程对目标进行卡尔曼滤波。在滤波过程中,滤波器对过去几个时刻组成的检测窗内新息序列的统计特性进行检验。根据新息序列的特性变化可判断目标有无机动,如有则用最小二乘法拟合出机动开始的时间和机动的幅度,并对当前状态补偿。
如果机动恒定,IE有很好的跟踪效果,且检测窗的长度越长,跟踪效果越好。当机动加速度变化时,检测窗内的机动幅度不再恒定,IE的跟踪效果会迅速恶化。为能在极坐标系中用IE对各种机动全面自适应跟踪,假设检测窗内机动阶梯变化,用UCM对观测值进行修正,应用于IE的算法模型,取得了很好的效果。
1.1 状态方程
目标运动状态方程如下:

式中,k是当前时刻;xk是系统状态变量,其分量是目标位置和速度;wk是系统过程噪声;Fk,k-1是系统状态转移矩阵;Gk,k-1是噪声输入矩阵;假设目标从时刻n开始机动,s=k-n是检测窗长度。时刻n以后目标实际运动方程为

式中,uk-1代表k-1时刻机动幅度的大小;Ck,k-1是输入控制矩阵。后续分析假设Fk,k-1=F,Gk,k-1=G,Ck,k-1=C。
假设^xmk,k是对n时刻机动un已知时的状态估计,^xk,k是不考虑un情况下的状态估计,Kj是j时刻卡尔曼滤波增益,则有
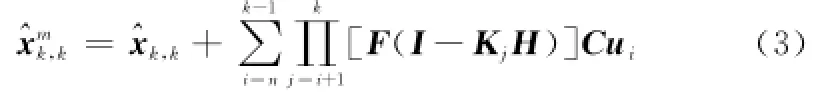
IE假设机动不变,这里为使算法有更强的鲁棒性,假设机动阶梯变化。假定机动起始时刻为n,则k时刻机动为

式中,un和uk分别表示n时刻和k时刻加速度向量;d是加速度阶梯增量;则式(3)变为

1.2 量测模型
目标量测方程如下:

式中,zk是直角坐标系的量测值;vk是量测噪声。实际的二维跟踪多在极坐标系进行,以雷达跟踪为例,其量测值多采用斜距rm和角度观测θm,方程为

式中,Xk和Yk代表k时刻目标在直角坐标系的位置。输入估计器对机动的估计要了解观测量在直角坐标系的统计特性,因此需将极坐标系的观测转换到直角坐标系。应用文献[15- 16]提出的修正UCM方法完成坐标变换,假设斜距和方位角观测误差相互独立且为零均值高斯噪声,标准差为σr和σθ。
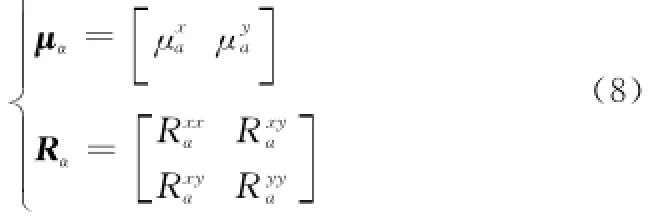
其中

将极坐标系量测值转换到直角坐标系有

转换后zk的协方差阵为Rα,可采用基于标准卡尔曼滤波器的IE技术对目标全面自适应跟踪。

其中

将式(9)改写成矩阵形式

其中


U是待估计量,ε满足高斯特性,其协方差矩阵为

应用最小二乘法可估计出U

待估计量U的协方差矩阵为
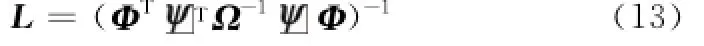
1.3 滤波步骤
卡尔曼滤波中,每个周期都要估计机动幅度,做机动判决,如有机动发生则对当前状态做相应修正和补偿。原有IE算法补偿时,将n~(k-1)时间段内的机动对k时刻状态影响全部消除后再递推到下一时刻。文献[7]中提出一种对状态部分补偿的方法,即只消除n时刻机动对k时刻状态影响,以便能对机动持续估计和检测,称为修正的IE算法,该算法与前面所提模型结合后的具体滤波步骤如下:
步骤1 用式(7)和式(8)将极坐标量测值转换至直角坐标系,并估计量测协方差阵;
步骤2 基于式(1)和式(6)对目标滤波跟踪;
步骤3 假设n=k-s,依据式(12)估计un和d;

步骤4 依据式(13)获得机动估计协方差阵后做机动判决其中,λ是机动判决门限,如无机动则系统输出y^k等于滤波值^x k

递推到下一时刻并返回步骤1,否则至步骤5;
步骤5 将步骤3估计出的un对新息序列和当前状态的影响消除,对误差矩阵做相应修正
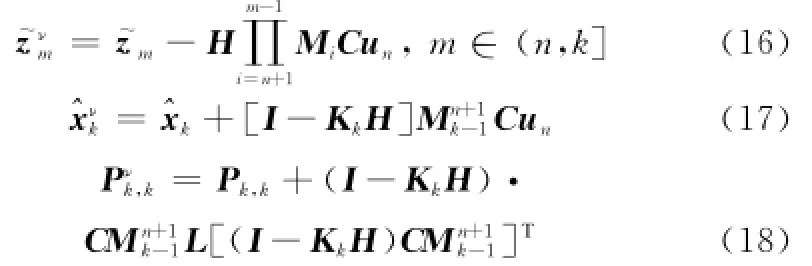
步骤6 将n~(k-1)时间段内的机动对k时刻状态的影响全补偿后输出,返回步骤1

2 仿真与分析
IMM算法因其对机动目标的全面自适应跟踪能力得到广泛应用。为评估本算法性能,将其与基于多滤波器并行工作的IMM相比较。场景1中,假设目标在二维平面内飞行,从(-10 000 m,3 000 m)处出发,匀速运动30 s后,在30~50 s间以(20 m/s2,20 m/s2)匀加速机动,在50~70 s间加速度线性递减直至恢复匀速运动。极坐标系量测的标准差为σr=20 m和σθ=0.1°,采样周期为1 s。对该场景采用基于扩展卡尔曼滤波的交互多模(IMM-extended Kalman filter,IMM-EKF)、IMM-IE及本文所提的UCM-IE算法分别进行跟踪,其中IMM-IE的量测也做了无偏转换处理。IMM-EKF基于3个模型,包含1个过程噪声为Q=0.01I的匀速模型,1个过程噪声为Q=I的匀加速模型和1个过程噪声为Q=9I的匀加速模型。马尔可夫概率转移矩阵为

IMM-IE基于2个过程噪声Q=0.01I的匀速模型,检测窗长度分别为6和4,检测门限都取8,马尔可夫概率矩阵为

UCM-IE算法的检测窗长度为10,检测门限取10。蒙特卡罗仿真次数为200次,仿真时长为120 s。图1(a)是仿真中目标和雷达探测器的位置配置关系。图1(b)是滤波跟踪中的位置估计误差,由于目标和探测器距离不同时,定位误差也不同,将滤波位置误差做归一化处理,定义归一化位置误差

图1(c)是各算法对加速度的跟踪情况。需要说明的是,输入估计器是在k时刻估计k~s时刻的机动幅度,因此其机动估计应在时间轴上前移s个时刻,IM M-IE使用了两种检测窗长度(4和6)的输入估计器,因此前移5个时刻,UCM-IE检测窗长度为10,前移10个时刻。图1(d)是IMM-IE和UCM-IE在各个时刻的机动检测概率。大。在整个机动跟踪过程中,UCM-IE和IMM-IE对加速度的跟踪较好,基本是无偏估计。而IMM-EKF由于包含一个匀速模型,其总体加速度估计是有偏估计,当加速度跟踪较好时(50~70 s),跟踪精度较好,否则(30~50 s)跟踪精度会下降。从图1(d)可见,IMM-IE的两个输入估计器的检测窗长度较短(长度分别为6和4),导致其对弱机动(70 s处)的检测概率较低,其在70 s处的估计误差变大;而UCM-IE采用较长的检测窗(长度为10),使其对弱机动的检测概率很高,估计误差稳定。

图1 场景1的跟踪性能对比
场景2采用文献[17]的连续转弯设置。目标从(30 000 m,30 000 m)出发,以速度(-172 m/s,-246 m/s)匀速运动20 s后右转弯机动,角速率为3.74 rad/s,48 s后左转弯机动,角速率为5.76 rad/s,32 s后恢复匀速运动。其他条件不变,仿真时长为150 s,仿真结果如图2所示。

从图1(b)中观察到:①UCM-IE对匀速运动的跟踪精度明显强于IMM-EKF,与IMM-IE相当;②UCM-IE的峰值估计误差(30 s附近)明显小于IMM-EKF,与IMM-IE相当;③UCM-IE在线性变加速度(50~70 s)段的跟踪精度稍弱于IMM-EKF,但与IMM-IE相当,3种算法在匀加速度(30~50 s)段的跟踪精度相当;④UCM-IE在弱机动处(70 s附近)的跟踪精度略高于IMM-IE。
UCM-IE与IMM-IE都基于匀速模型跟踪滤波,当已知目标噪声统计特性且无机动误检时,能对匀速过程最优滤波,因此二者的匀速段跟踪性能均强于IMM-EKF。由图1(c)可见,IMM-EKF在机动切换时刻(30 s处)对阶跃加速度的响应明显滞后其他算法,导致其峰值估计误差较

图2 场景2的跟踪性能对比
从图2(b)可见:①UCM-IE在20 s处的估计误差小于IMM-EKF,与IMM-IE相当;②3种算法在慢转弯段跟踪误差相同,在快转弯段,UCM-IE跟踪精度与IMM-IE相当,IMM-EKF算法最差;③UCM-IE在转弯切换处(68 s)跟踪精度最高,IMM-IE次之,IM M-EKF最差。
从图2(c)可见,IMM-EKF在20 s和68 s处的机动响应缓慢,导致其跟踪误差较大。图2(d)中68 s处加速度发生跳变,IMM-IE检测窗内机动加速度不变的假设导致其检测概率降低,估计误差变大;而UCM-IE的线性加速度假设更逼近实际机动,检测概率较高,跟踪误差稳定。
目标跟踪算法的实时性是不容忽视的因素,因此对3种算法的计算复杂度做了比较。在奔腾双核2.8 GHz的计算机上,Matlab仿真300次的运行时间如表1所示。

表1 算法运行时间对比s
综上可见,UCM-IE与传统IM M-EKF相比,跟踪性能上有显著提高,而计算量接近;与IM M-IE相比,性能相当,计算量降低一倍,是一种实用性很强的全面自适应跟踪算法。
3 结 论
IE能精确跟踪匀速运动,且无需任何目标机动特性的先验知识,在目标跟踪研究领域有重要地位,但迄今为止,没有将IE用于雷达探测系统的实用算法。针对此,本文提出基于UCM和单个输入估计器的跟踪算法。提出检测窗内加速度阶梯变化的假设,推导了相应的滤波公式,并将极坐标系量测无偏转换到直角坐标系内完成机动检测、估计与补偿。检测窗内加速度变化的假设使得算法有更强的全面自适应性,可以用更长的检测窗跟踪诸如弱机动、阶跃加速度等各种机动,且计算量未有明显提升。仿真实验与原理分析验证了算法的稳健性,为IE用于工程实践打下基础。
[1]Han C Z.Multi source information fusion[M].2nd ed.Beijing:Tsinghua University Press,2010.(韩崇昭.多源信息融合[M].2版.北京:清华大学出版社,2010.)
[2]Chan Y T,Hu A G C,Plant J B.A Kalman filter based tracking scheme with input estimation[J].IEEE Trans.on Aerospace and Electronic Systems,1979,15(2):237- 244.
[3]Bogler P L.Tracking a maneuvering target using input estimation[J].IEEE Trans.on AES,1987,23(3):298- 310.
[4]Wang T C,Varshney P K.A tracking algorithm for maneuvering targets[J].IEEE Trans.on AES,1993,29(3):910- 924.
[5]Whang I H,Lee J,Sung T.Modified input estimation technique using pseudo-residuals[J].IEEE Trans.on AES,1994,30(1):220- 228.
[6]Li X R,Jilkov V P.A survey of maneuvering target tracking-part IV:decision-based methods[C]∥Proc.of SPIE Conference Signal and Data Processing of Small Targets,2002,4728:511- 534.
[7]Sheng H,Yang J S.Maneuvering target tracking algorithm based on modification of innovation sequence[J].Systems Engineering and Electronics,2009,31(9):2121- 2124.(盛琥,杨景曙.基于新息序列修正的机动目标跟踪算法[J].系统工程与电子技术,2009,31(9):2121- 2124.)
[8]Sheng H,Yang J S.Interacting multiple model tracking algorithm with modified input estimation[J].Acta Electronica Sinica,2009,37(12):2810- 2814.(盛琥,杨景曙.引入输入估计的交互式多模跟踪算法[J].电子学报,2009,37(12):2810- 2814.)
[9]Song L P,Ji H B.Modified input estimation with interacting fading memory for maneuvering target tracking[C]∥Proc.of the 2nd International Conference on Signal Processing Systems,2010:448- 451.
[10]Ben Hmida F,Ragot J.Three-stage Kalman filter for state and fault estimation of linear stochastic systems with unknown inputs[J].Journal of the Franklin Institute,2012,349(7):2369- 2388.
[11]Bordonaro S V,Bias P W.Elimination in tracking with converted position and Doppler measurements[C]∥Proc.of the 51st IEEE Conference on Decision and Control,2012:4089- 4094.
[12]Bordonaro S V,Yaakov B-S P W,Unbiased tracking with converted measurements[C]∥Proc.of the IEEE Radar Conference,2012:741- 745.
[13]Mao Y H,Li X R,Duan Z S.Unbiased measurement model conversion for tracking with multiple radars or sonars[C]∥Proc. of the 31st Chinese Control Conference,2012:897- 903.
[14]Valarmathi J.Tracking using converted measurement Kalman filter through improved algorithm in the missed detections scenario[C]∥Proc.of the 1st Workshop on Emerging Technologies and Devices in Signal Processing,2012:1010- 1015.
[15]Duan Z S,Han C Z,Li X R.Comments on“unbiased converted measurements for tracking”[J].IEEE Trans.on Aerospace and Electronic Systems,2004,40(4):1374- 1377.
[16]Spitzmiller J N.Tracking with spherical-estimate-conditioned debiased converted measurements[C]∥Proc.of the IEEE Radar Conference,2010:134- 139.
[17]Yaakov BS,William D B.Multi-target multi-sensor tracking:applications and advance[M].Boston:Artech House,2000.
融合、统计信号处理。
E-mail:13955168560@139.com
王立明(1974-),男,讲师,博士,主要研究方向为无人机技术与应用。
E-mail:wanglm@aiofm.ac.cn
刘发磊(1982-),男,讲师,硕士,主要研究方向为无人机技术与应用。
E-mail:tiger0136@163.com
曹 燕(1977-),女,讲师,硕士,主要研究方向为新型计算机控制系统与控制网络。
E-mail:cy961102@163.com
Maneuvering target tracking algorithm based on converted measurement and input estimation
SHENG Hu,ZHAO Wen-bo,WANG Li-ming,LIU Fa-lei,CAO Yan
(Army Officer Academy,Hefei 230031,China)
An overall adaptive tracking algorithm is proposed to estimate state variables of maneuvering target.Combining with unbiased converted measurement(UCM)technique to convert polar measurements to Cartesian coordinate,input estimation(IE)can be manipulated in polar coordinate.After assuming the acceleration within detection window is linear step distributed,the derivation of relevant model is made,so a singleinput estimator can track variable maneuver level.Simulation results for different target profiles are included.Compared with the interactive multiple model algorithm which is based on concurrent working of multiple filters,the scheme is comparablein terms of tracking performance while the computation complexity can be significantly reduced,so the proposed algorithm is suitable to application with high demand for performance and efficiency,which makes it a promising algorithm.
overall adaptive tracking;variable acceleration tracking;input estimation(IE);unbiased converted measurement
TN 953
A
10.3969/j.issn.1001-506X.2015.01.06
盛 琥(1980-),男,讲师,博士,主要研究方向为卫星导航、无源定位、机动目标跟踪。
E-mail:tigersh_2000@aliyun.com
赵温波(1972-),男,副教授,博士,主要研究方向为目标跟踪、数据
1001-506X(2015)01-0031-06
网址:www.sys-ele.com
2013- 10- 28;
2014- 04- 28;网络优先出版日期:2014- 06- 30。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20140630.1258.002.html
国家自然科学基金(61273001);安徽省自然科学基金(1208085QF109)资助课题
