以“问”促思,以“探”激能
2015-06-16朱铭丽章薇薇
朱铭丽++++章薇薇
[摘 要] 将师生在课堂中发生的案例或片段进行整合与分析,结合学生数学小论文的操作对课堂生成、呈现、规范进行掌控,及时调整教学策略,能推动数学课堂的精彩生成,在提高课堂效益的同时,更能提高本身思维的宽厚度.
[关键词] 高效课堂;课堂操作;数学小论文
李炳亭先生说:高效课堂是知识的超市,生命的狂欢. 而其必须解决两“率”——课堂精力流失率和提高高效学习率. 的确,要想抓住这两“率”,作为教师的我们就必须满足不同需求的孩子,精心设计好课堂环节,充分调动孩子的各种“学习力”,给予学生足够的思考与创造时间,让其“展示”以促其“内驱力”,进而使其能快乐而高效地学习.
■ 课堂设计:选,问,引,精致化——一石激起千层浪
一堂高效的数学课,源于课堂素材选用得当、有效,课堂例题挖掘充分,点拨精进恰当,数学思想方法渗透扎实到位,使课堂流程设计精致化,课堂设问循序渐进,课堂引导符合学生的最近发展区,从而使学生在课堂上获得最佳发展.
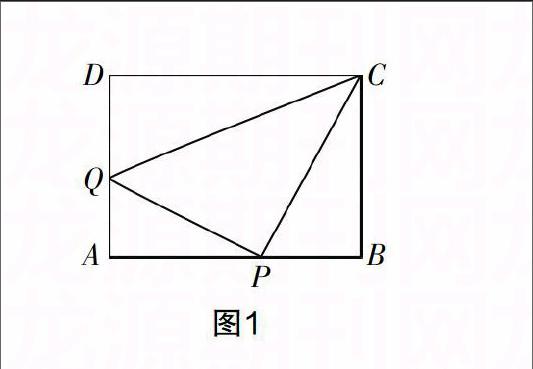
案例1?摇 如图1所示,在矩形ABCD中,AB=24 cm,BC=12 cm,点P以2 cm/s的速度从点A开始沿边AB向点B移动,点Q以1 cm/s的速度从点D开始沿边DA向点A移动,如果点P,Q同时出发,用t(s)表示移动的时间(1≤t≤12),那么当t为何值时,△QAP的面积等于32 cm2 ?
以此题为背景,学生经过思考,还设计了以下追问:
(1)t为何值时,点P,Q相距6■ cm?
(2)t为何值时,PQ⊥CP?
(3)是否存在这样的t,使得△QCP的面积等于109 cm2 ?
(4)t为何值时,△QCP为直角三角形?
(5)将题改为:在矩形ABCD中,AB=24 cm,BC=12 cm,点P以2 cm/s的速度从点A开始沿边AB—BC向点C移动,点Q以1 cm/s的速度从点D开始沿边DA向点A移动,到达点A后即刻返回D点,如果点P,Q同时出发,用t(s)表示移动的时间(1≤t≤18),则t为何值时,PQ=30 cm?
本题涉及很多数学思想方法,如转化思想、化斜为直、分类讨论等,也用到了很多常见模型,如“K字型”证相似等. 学生在自己设计题目的过程中,教师不光要仔细聆听,还要及时加以点拨与引导,使学生能将本图看得更透彻,同时,对于学生反馈的错误,需耐心地剖析,让他们知其然,更知其所以然.
这样高效利用课堂资源,以一图为背景将数字知识、数学本质与数学结论抽丝剥茧式慢慢呈现在学生面前,更有利于学生掌握与获取.
■ 课堂呈现:视、听、触,多样化——操千曲而后晓声
心理学实验材料表明:“人对信息的接受,味觉占1%,触觉占1.5%,嗅觉占3.5%,听觉占11%,视觉占83%,其中视听两项合计达94%. 而人对信息的记忆保存,仅靠视觉为25%,仅靠听觉为15%,视听结合可达65%. ”
这个实验材料告诉我们,课堂教学如果只是局限于听讲,而不注重调动其他感觉器官的话,课堂效果是无法达到最佳的.
以前教师上数学课喜欢用小黑板,不仅可以增加课堂容量,还可以用不同颜色的粉笔对例题进行圈点作标记,便于学生剖析例题,理解与分析问题. 这样的教学呈现是将学生的听觉与视觉相结合,在加深记忆的同时,也有学生自己的新认识与生成.
然而,自从有了多媒体之后,数学课堂的呈现方式也变得异常热闹,如几何画板呈现动态的生成过程,PPT课件的导入,使原本只是数字与字母、图形构成的数学课堂,变得相当色彩鲜艳,容量大增,故高效的数学课堂是以呈现方式为手段,以一个问题为发散点,使学生与教师的思维同步,将学生的思维错误作为生成的资源纳入课堂,通过讲、演、问、说、探等方式、方法使学生的知识得以强化,思想得以升华,能力得以提升.
我们利用多媒体上课时,可以调动学生的多种感觉器官,集中学生的注意力,在确保学生主动积极接受知识的同时,更扩大课堂容量,让学生在课堂上学有所得,学有所乐,进而减轻学生课外的学业负担. 利用多样化的呈现方式,也可以促进学生学习习惯的养成、思维能力的提升,进而更好地提高课堂效率.
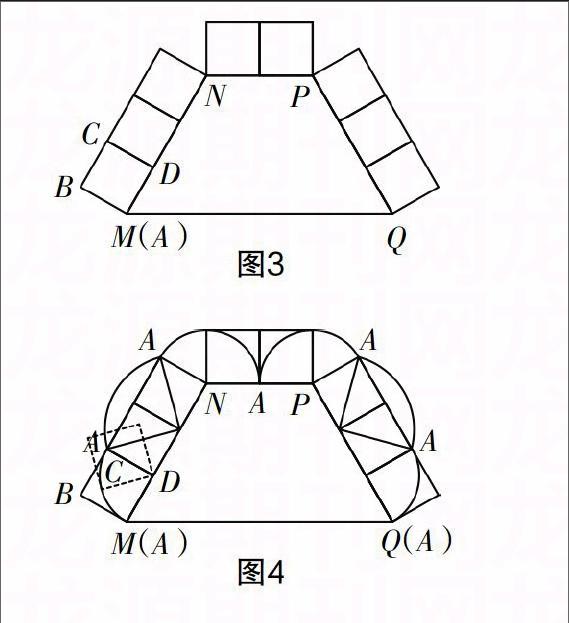
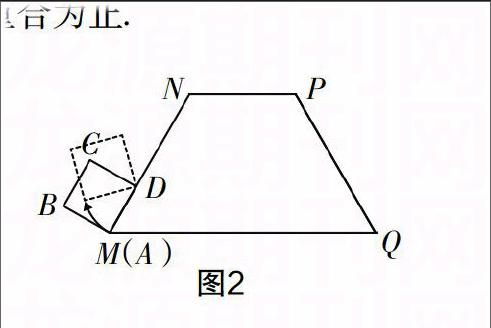
案例2?摇 如图2所示,等腰梯形MNPQ的上底长为2,腰长为3,一个底角∠NMQ为60°,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与点M重合. 现将正方形ABCD在梯形的外面沿边MN,NP,PQ进行翻滚,翻滚到有一个顶点与点Q重合为止.
■
(1)请在所给的图中,用尺规画出点A在正方形整个翻滚过程中所经过的路线图;
(2)求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN,NP,PQ所围成图形的面积S.
本题的讲解,利用几何画板展示正方形的滚动情况,让学生观察点A在滚动中位置的确定,并点好相应位置,再画出弧线,表面看来,学生对信息的接受效果很好,纷纷表示懂了,但让自己画画试试看时,发现会画的学生没几人,也就是说,光看动画演示没法让学生真正掌握,所以,我要求学生自制一个小正方形,标好顶点A,并在图3中标示出点A每次滚动后的位置,让学生思考点A形成的路径是什么形状,要画出这个形状,我们要找到哪些关系的量?经过点拨、操作与思考,大部分学生画出了正确图形(如图4),相信他们也真正掌握了此类滚动类考题的基本方法技巧,而这个是几何画板所无法给予的.
■
■
■ 课堂生成:题,法,文,多元化—— 一花独放不是春
精彩的课堂能激发学生的潜力,让学生乐在其中,提高效益,生成能力. 简约而质朴的课堂设计能让学生发现问题、思考问题,最后,把各种“问号”转化为“句号”或“叹号”. 扎实有效的课堂,鼓励学生思维有张有弛,双边互动,让师生在头脑风暴式的相互追问下,将课堂在不停的预设中构成新的生成. 课堂的智慧、高潮、价值尽在“不可预设”的“现场生成”上,一切的预设应服务于“现场”,而不是让“现场”服务于预设. 笔者对“学生讲题”及“学生小论文”进行了研究与尝试. 如课前五分钟学生讲题,如课中的精彩一刻等形式,学生会自己选出一个自己想讲的题,为大家进行讲解和分析,这样的课堂由于有学生的高度参与而显得格外充满生机与活力.endprint
案例3?摇 学生讲题——不可取的“瘦身”
九年级(3)班 吴 洁
今天考卷上做了一题,是关于一元二次方程的,原来我沾沾自喜,想着马上就会有一个大大的勾了,可不料,老师打了一个叉.
怎么会?我错哪儿了?于是我认真地检查了一下.
原题——证明:无论a取何值,关于x的一元二次方程x2-(2a-3)x+a-3=0有两个不相等的实数根.
原解:x2-(2a-3)x+a-3=0,因为Δ=(2a-3)2-4×1×(a-3)=4a2-16a+21=a2-4a+■=(a-2)2+■>0,且抛物线开口向上,所以无论a取何值,一元二次方程x2-(2a-3)x+a-3=0都有两个不相等的实数根.
我左看右看,终于发现了问题,我为这个方程“瘦了身”,使它整整缩小了4倍,意识到这个问题,我幡然醒悟.
总结:在代数式中,千万不能给代数式“瘦身”,一定要把系数提出来.
正解:x2-(2a-3)x+a-3=0,因为Δ=(2a-3)2-4×1×(a-3)=4a2-16a+21=4(a2-4a+4)+5=4(a-2)2+5>0,且抛物线开口向上,所以无论a取何值,一元二次方程x2-(2a-3)x+a-3=0都有两个不相等的实数根.
为了更好地记住这个错误,我反思一定要把系数提出来吗?可是我们已经习惯了将二次项系数化为1了呀,毕竟这样可以化繁为简. 若一定要化系数为1,就必须等式的左、右两边同时进行,那若真把它当成等式来做,可以吗?于是我又做了如下尝试:
因为Δ=(2a-3)2-4×1×(a-3)=4a2-16a+21,所以■=a2-4a+■.?摇
■=a2-4a+4+■=(a-2)2+■,即Δ=4(a-2)2+5.
这样操作居然成功了,我相信,以后再遇到这样的问题,我再也不会做错了.
教师点评:适合学生的方法才是最好的方法,相信这个学生得到的方法,是在学生易错点处的点拨,这样的处理方法符合学生的认知水平,也符合学生的解题思维,是有效学习的结果.
有效的教学活动是学生“学”与教师“教”的统一,学生是学习的主体. 是的,真正的有效是学生发自内心深处的想要学数学、解决数学问题. 让学生上讲台解数学题目、写数学小论文,而教师在旁聆听,关注课堂的新生成,能在了解学生思维的同时,为以后的教学起到提示与扩充的作用,这样不光能以“误”唤起百转思,更能以“讲”激起千层浪.
第斯多惠说:“教学的艺术,不在于传授本领,而在于激励、唤醒、鼓舞. ”我想,一个高效的课堂必将是一个揪住知识点“无限”放大,调动学生全身心投入,并在不断思考中、教师的追问下、自己的实践反思下,不断完善自己,进而实现自己最优化发展的课堂.endprint
